Python 中的机器学习简介:多项式回归
一、说明
多项式回归可以识别自变量和因变量之间的非线性关系。本文是关于回归、梯度下降和 MSE 系列文章的第三篇。前面的文章介绍了简单线性回归、回归的正态方程和多元线性回归。
二、多项式回归
多项式回归用于最适合曲线拟合的复杂数据。它可以被视为多元线性回归的子集。
![]()
请注意,X₀ 是偏差的一列;这允许在第一篇文章中讨论的广义公式。使用上述等式,每个“自变量”都可以被视为 X₁ 的指数版本。
![]()
![]()
![]()
这允许从多元线性回归使用相同的模型,因为只需要识别每个变量的系数。可以创建一个简单的三阶多项式模型作为示例。其等式如下:
![]()
![]()
![]()
![]()
模型、梯度下降和 MSE 的广义函数可用于前面的文章:
# line of best fit
def model(w, X):"""Inputs:w: array of weights | (num features, 1)X: array of inputs | (n samples, num features)Output:returns the output of X@w | (n samples, 1)"""return torch.matmul(X, w)# mean squared error (MSE)
def MSE(Yhat, Y):"""Inputs:Yhat: array of predictions | (n samples, 1)Y: array of expected outputs | (n samples, 1)Output:returns the loss of the model, which is a scalar"""return torch.mean((Yhat-Y)**2) # mean((error)^2)# optimizer
def gradient_descent(w):"""Inputs:w: array of weights | (num features, 1)Global Variables / Constants:X: array of inputs | (n samples, num features)Y: array of expected outputs | (n samples, 1)lr: learning rate to scale the gradientOutput:returns the updated weights""" n = X.shape[0]return w - (lr * 2/n) * (torch.matmul(-Y.T, X) + torch.matmul(torch.matmul(w.T, X.T), X)).reshape(w.shape)三、创建数据
现在,所需要的只是一些用于训练模型的数据。可以使用“蓝图”功能,并且可以添加随机性。这遵循与前面文章相同的方法。蓝图如下所示:
![]()
可以创建大小为 (800, 4) 的训练集和大小为 (200, 4) 的测试集。请注意,除偏差外,每个特征都是第一个特征的指数版本。
import torchtorch.manual_seed(5)
torch.set_printoptions(precision=2)# features
X0 = torch.ones((1000,1))
X1 = (100*(torch.rand(1000) - 0.5)).reshape(-1,1) # generates 1000 random numbers from -50 to 50
X2, X3 = X1**2, X1**3
X = torch.hstack((X0,X1,X2,X3))# normal distribution with a mean of 0 and std of 8
normal = torch.distributions.Normal(loc=0, scale=8)# targets
Y = (3*X[:,3] + 2*X[:,2] + 1*X[:,1] + 5 + normal.sample(torch.ones(1000).shape)).reshape(-1,1)# train, test
Xtrain, Xtest = X[:800], X[800:]
Ytrain, Ytest = Y[:800], Y[800:]定义初始权重后,可以使用最佳拟合线绘制数据。
torch.manual_seed(5)
w = torch.rand(size=(4, 1))
wtensor([[0.83],[0.13],[0.91],[0.82]])import matplotlib.pyplot as pltdef plot_lbf():"""Output:prints the line of best fit in comparison to the train and test data"""# plot the train and test setsplt.scatter(Xtrain[:,1],Ytrain,label="train")plt.scatter(Xtest[:,1],Ytest,label="test")# plot the line of best fitX1_plot = torch.arange(-50, 50.1,.1).reshape(-1,1) X2_plot, X3_plot = X1_plot**2, X1_plot**3X0_plot = torch.ones(X1_plot.shape)X_plot = torch.hstack((X0_plot,X1_plot,X2_plot,X3_plot))plt.plot(X1_plot.flatten(), model(w, X_plot).flatten(), color="red", zorder=4)plt.xlim(-50, 50)plt.xlabel("$X$")plt.ylabel("$Y$")plt.legend()plt.show()plot_lbf()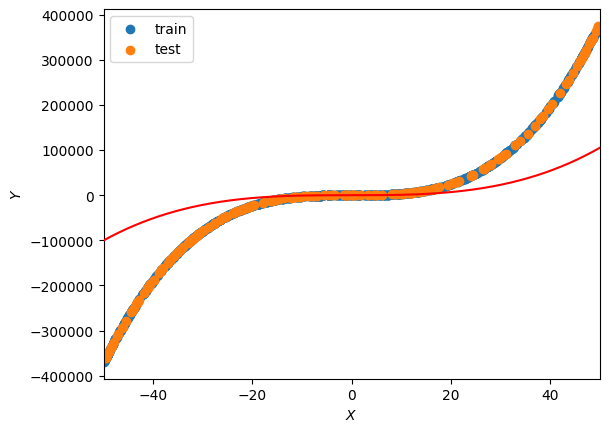
四、训练模型
为了部分最小化成本函数,可以使用 5e-11 和 500,000 epoch 的学习率与梯度下降一起使用。
lr = 5e-11
epochs = 500000# update the weights 1000 times
for i in range(0, epochs):# update the weightsw = gradient_descent(w)# print the new values every 10 iterationsif (i+1) % 100000 == 0:print("epoch:", i+1)print("weights:", w)print("Train MSE:", MSE(model(w,Xtrain), Ytrain))print("Test MSE:", MSE(model(w,Xtest), Ytest))print("="*10)plot_lbf()epoch: 100000
weights: tensor([[0.83],[0.13],[2.00],[3.00]])
Train MSE: tensor(163.87)
Test MSE: tensor(162.55)
==========
epoch: 200000
weights: tensor([[0.83],[0.13],[2.00],[3.00]])
Train MSE: tensor(163.52)
Test MSE: tensor(162.22)
==========
epoch: 300000
weights: tensor([[0.83],[0.13],[2.00],[3.00]])
Train MSE: tensor(163.19)
Test MSE: tensor(161.89)
==========
epoch: 400000
weights: tensor([[0.83],[0.13],[2.00],[3.00]])
Train MSE: tensor(162.85)
Test MSE: tensor(161.57)
==========
epoch: 500000
weights: tensor([[0.83],[0.13],[2.00],[3.00]])
Train MSE: tensor(162.51)
Test MSE: tensor(161.24)
==========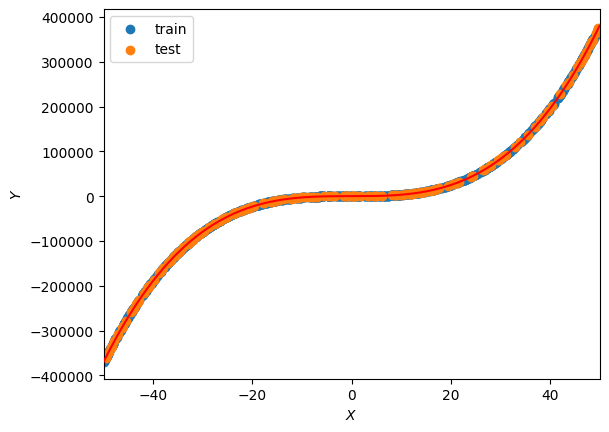
即使有 500,000 个 epoch 和极小的学习率,该模型也无法识别前两个权重。虽然当前的解决方案非常准确,MSE为161.24,但可能需要数百万个epoch才能完全最小化它。这是多项式回归梯度下降的局限性之一。
五、正态方程
作为替代方案,可以使用第二篇文章中的正态方程直接计算优化权重:
def NormalEquation(X, Y):"""Inputs:X: array of input values | (n samples, num features)Y: array of expected outputs | (n samples, 1)Output:returns the optimized weights | (num features, 1)"""return torch.inverse(X.T @ X) @ X.T @ Yw = NormalEquation(Xtrain, Ytrain)
wtensor([[4.57],[0.98],[2.00],[3.00]])正态方程能够立即识别每个权重的正确值,并且每组的MSE比梯度下降时低约100点:
MSE(model(w,Xtrain), Ytrain), MSE(model(w,Xtest), Ytest)(tensor(60.64), tensor(63.84))六、结论
通过实现简单线性、多重线性和多项式回归,接下来的两篇文章将介绍套索和岭回归。这些类型的回归在机器学习中引入了两个重要概念:过拟合和正则化。
参考文章:
亨特·菲利普斯
相关文章:

Python 中的机器学习简介:多项式回归
一、说明 多项式回归可以识别自变量和因变量之间的非线性关系。本文是关于回归、梯度下降和 MSE 系列文章的第三篇。前面的文章介绍了简单线性回归、回归的正态方程和多元线性回归。 二、多项式回归 多项式回归用于最适合曲线拟合的复杂数据。它可以被视为多元线性回归的子集。…...

docker 容器中执行命令出现错误: 13: Permission denied
错误 13: Permission denied [rootVM-32-11-tencentos ~]# docker exec -it kibana1 /bin/bash kibana76c20c215dcb:~$ apt-get install vi E: Could not open lock file /var/lib/dpkg/lock-frontend - open (13: Permission denied) E: Unable to acquire the dpkg frontend…...

JavaWeb学习|JavaBean;MVC三层架构;Filter;Listener
1.JavaBean 实体类 JavaBean有特定的写法: 必须要有一个无参构造 属性必须私有化。 必须有对应的get/set方法 用来和数据库的字段做映射 ORM; ORM:对象关系映射 表--->类 字段-->属性 行记录---->对象 2.<jsp:useBean 标签 3. MVC三层架构 4. Filter …...
的添加、删除、卸载和重载_objectarx)
arx 外部参照文件(XREF)的添加、删除、卸载和重载_objectarx
添加参照 CString strFileName;int nIndex = strFilePath.ReverseFind(\\);if (nIndex != -1){strFileName = strFilePath.Right(strFilePath....

【博客699】docker daemon预置iptables剖析
docker daemon预置iptables剖析 没有安装docker的机器:iptables为空,且每个链路的默认policy均为ACCEPT [root~]# iptables-save[root ~]# iptables -t raw -nvL Chain PREROUTING (policy ACCEPT 0 packets, 0 bytes)pkts bytes target prot opt …...

Golang 中的交叉编译详解
Golang 中的交叉编译 在 Golang 中,交叉编译指的是在同一台机器上生成针对不同操作系统或硬件架构的二进制文件。这在开发跨平台应用或构建特定平台的发布版本时非常有用。 交叉编译 Golang 程序的基本步骤如下: 指定目标操作系统和工具链并设置对应的…...

Python中的诡异事:不可见字符!
文章目录 前言1. 起因2. 调查3. 高能4. 释惑 前言 今天分享一件很诡异的事情,我写代码的时候遇到了不可见的字符!!! 1. 起因 今天在使用pipreqs导出项目中所依赖的库时突然报错了: pipreqs . --encodingutf-8 --forc…...
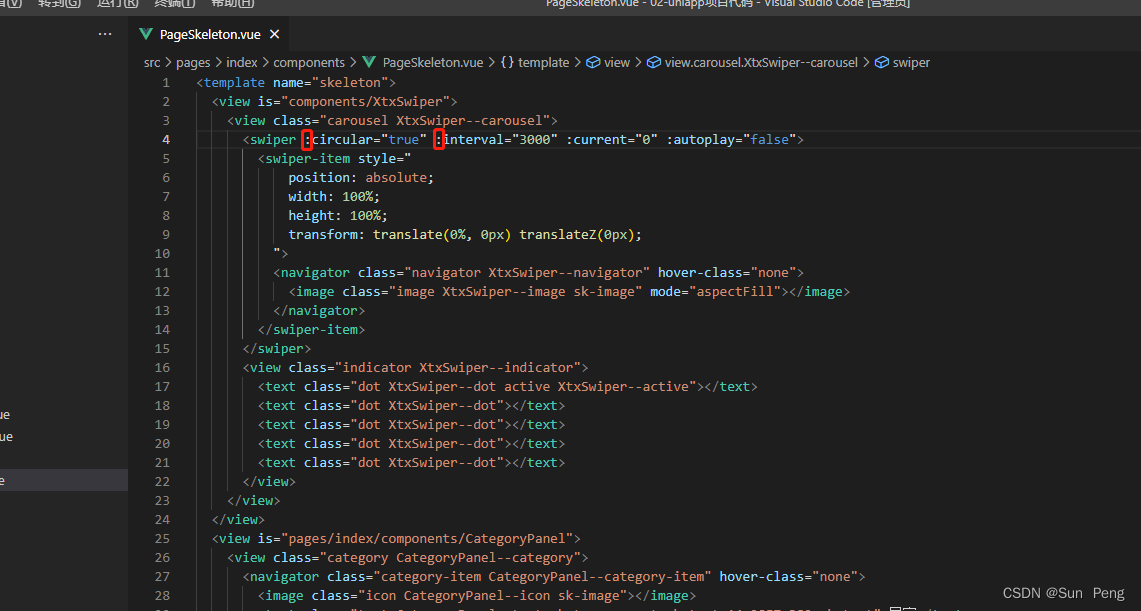
【uniapp】uniapp使用微信开发者工具制作骨架屏:
文章目录 一、效果:二、过程: 一、效果: 二、过程: 【1】微信开发者工具打开项目,生成骨架屏,将wxml改造为vue页面组件,并放入样式 【2】页面使用骨架屏组件 【3】改造骨架屏(去除…...
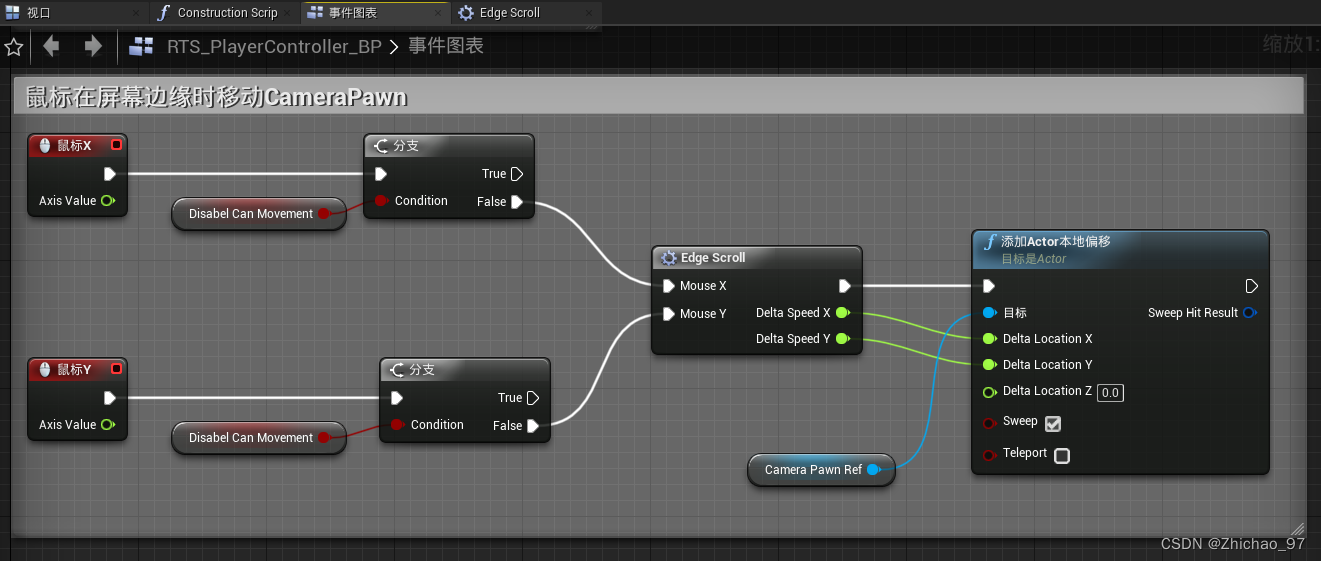
【UE4 RTS】06-Camera Edge Scroll
前言 本篇实现的效果是当玩家将鼠标移至屏幕边缘时,视野会相应的上下左右移动 效果 步骤 1. 打开玩家控制器“RTS_PlayerController_BP”,在类默认值中设置如下选项 新建一个宏,命名为“EdgeSroll”, 添加两个输入和三个输出&a…...

无涯教程-Perl - length函数
描述 此函数返回EXPR值的长度(以字符为单位),如果未指定,则返回$_。如果要确定相应的大小,请在数组或哈希上使用标量context。 语法 以下是此函数的简单语法- length EXPRlength返回值 此函数返回字符串的大小。 例 以下是显示其基本用法的示例代码- #!/usr/bin/perl$o…...

怎样在 CentOS 里下载 RPM 包及其所有依赖包
前几天我尝试去创建一个仅包含我们经常在 CentOS 7 下使用的软件的本地仓库。当然,我们可以使用 curl 或者 wget 下载任何软件包,然而这些命令并不能下载要求的依赖软件包。你必须去花一些时间而且手动的去寻找和下载被安装的软件所依赖的软件包。然而,我们并不是必须这样。…...

在Ubuntu上使用NFS挂载
假设要把192.16.2.101服务器上的 /home/sharedata 挂载到192.16.2.102服务器上的 /home/receive_data 一、服务端 1、安装NFS服务端 sudo apt-get install nfs-kernel-server 2、修改NFS挂载配置文件 sudo vim /etc/exports 在文件中输入 /home/sharedata 192.16.2.102(…...

复现海康威视综合安防管理平台artemis接口Spring boot heapdump内存泄露漏洞
目录 一、漏洞描述 二、影响版本 三、资产测绘 四、漏洞复现 一、漏洞描述 HIKVISION iSecure Center综合安防管理平台是一套“集成化”、“智能化”的平台,通过接入视频监控、一卡通...
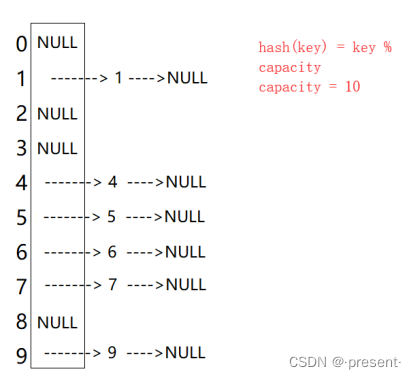
哈希unordered系列介绍(上)
一.Unordered_map,Unordered_set介绍 在之前我们已经介绍过set,map,multiset等等关联式容器,它们的底层是红黑树进行模拟实现的,在查询时效率可达到 l o g 2 N log_2 N log2N,即最差情况下需要比较红黑树的高度次,当树中的节点…...

MySQL随心记第二篇
一、正则表达式篇: regular expression--> regexp 元字符: . : 单个的任意字符(默认不包含换行) \d:数字: 0-9 补集:\D \w:ascil:数字,大写字母,小写字母,以及下划线 unicode: 数字,大…...
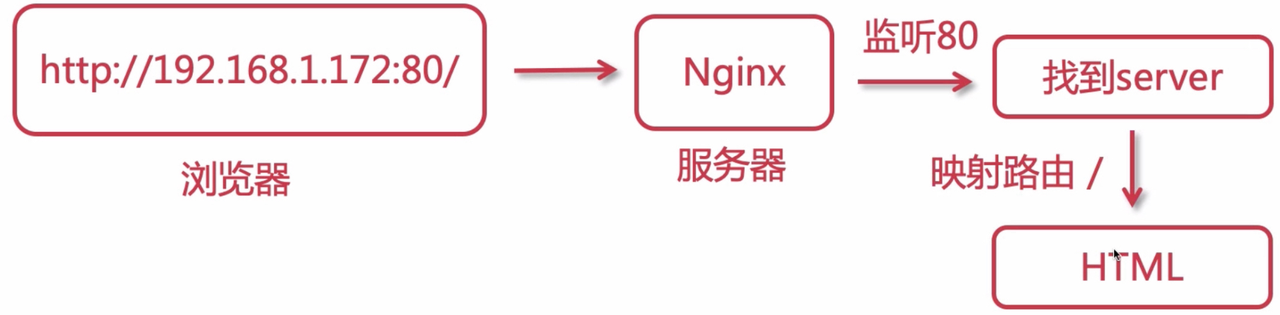
0001nginx简介、相关模型与原理
文章目录 一. 什么是Nginx二. ngnix的一些模型1、nginx的进程模型2、worker的抢占(锁)机制模型3. nginx事件处理模型 三. nginx加载静态资源的过程 一. 什么是Nginx Nginx是一个高性能HTTP反向代理服务器,以下是nginx的相关能力 反向代理&am…...
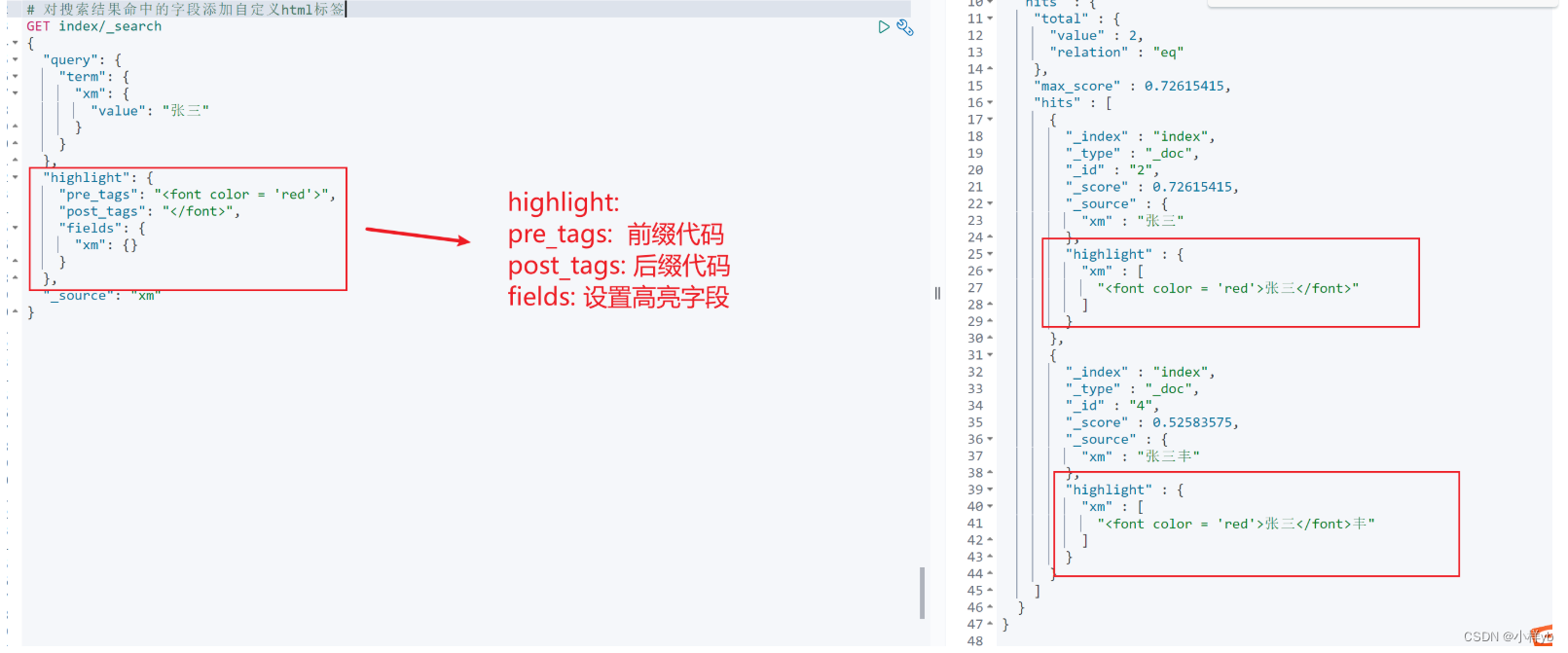
elasticsearch简单入门语法
基本操作 创建不同的分词器 ik_smart: 极简分词 ; ik_max_word: 最细力再度分词 基本的rest命令 methodurl地址描述PUTlocalhost:9200/索引名称/类型名称/文档id创建文档(指定文档id)POSTlocalhost:9200/索引名称/类型名称创建文…...

Python自动化测试用例:如何优雅的完成Json格式数据断言
目录 前言 直接使用 优化 封装 小结 进阶 总结 资料获取方法 前言 记录Json断言在工作中的应用进阶。 直接使用 很早以前写过一篇博客,记录当时获取一个多级json中指定key的数据: #! /usr/bin/python # coding:utf-8 """ aut…...

阿里云对象存储服务OSS
1、引依赖 <dependency><groupId>com.aliyun.oss</groupId><artifactId>aliyun-sdk-oss</artifactId><version>3.15.1</version> </dependency> <dependency><groupId>javax.xml.bind</groupId><artifa…...
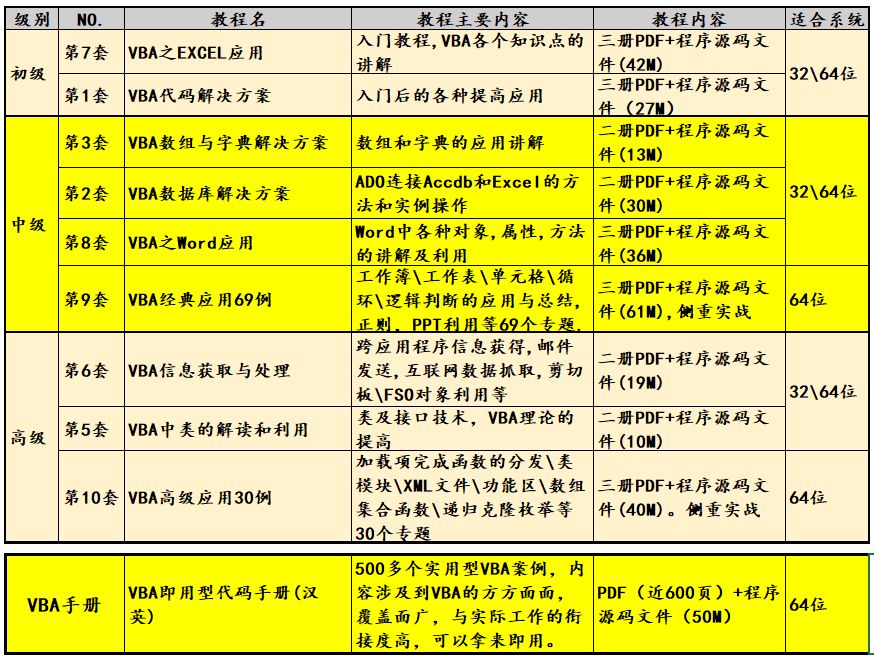
第三节:在WORD为应用主窗口下关闭EXCEL的操作(1)
【分享成果,随喜正能量】夏日里的遗憾,一定都会被秋风温柔化解。吃素不难,难于不肯捨贪口腹之心。若不贪口腹,有何吃素之不便乎。虽吃华素,不吃素日,亦须少吃。以一切物类,皆是贪生怕死…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...
