YOLOv5基础知识入门(5)— 损失函数(IoU、GIoU、DIoU、CIoU和EIoU)

前言:Hello大家好,我是小哥谈。使用YOLOv5训练模型阶段,需要用到损失函数。损失函数是用来衡量模型预测值和真实值不一样的程度,极大程度上决定了模型的性能。本节就给大家介绍IoU系列损失函数,希望大家学习之后能够有所收获!🌈
![]() 前期回顾:
前期回顾:
YOLOv5基础知识入门(1)— YOLO算法的发展历程
YOLOv5基础知识入门(2)— YOLOv5核心基础知识讲解
YOLOv5基础知识入门(3)— 目标检测相关知识点
YOLOv5基础知识入门(4)— 神经网络的基本概念与原理
目录
🚀1.损失函数简介
🚀2.IoU
🚀3.GIoU
🚀4.DIoU
🚀5.CIoU
🚀6.EIoU
🚀7.总结

🚀1.损失函数简介
损失函数(loss function)是用于衡量模型预测结果与真实结果之间的差距。损失函数通常是一标量函数,其值越小表示模型的预测结果越接近真实结果,反之则表示预测结果与真实结果之间的差距越大。🎈
使用YOLOv5训练模型的时候,我们需要不断地调整模型的参数,使得模型的预测结果和真实结果之间的差距最小化,损失函数在这个过程中起到了关键的作用。它可以帮助我们衡量模型的预测结果与真实结果之间的差距,并将这个差距转化为一个标量值。我们可以使用这个标量值来评估模型的性能,并根据这个标量值来调整模型的参数。🍓
YOLOv5损失函数包括:
- classification loss,分类损失
- localization loss,定位损失(预测边界框与GT之间的误差)
- confidence loss,置信度损失(框的目标性;objectness of the box)
总体损失函数:Loss = a*classification loss + b*localization loss + c*confidence los
也即总体损失函数为三个损失函数的加权和,通常置信度损失函数取最大权重,矩形框损失函数和分类损失的权重次之。🌷
🚀2.IoU
IoU(Intersection over Union),为两个方框相交区域面积与相并区域面积的比值,所以也称为交并比。❤️

🍀计算公式:

🍀不足之处:
具体如下图所示:👇
(1)即状态1的情况,当预测框和目标框不相交时,IOU=0,无法反应两个框距离的远近,此时损失函数不可导,IOU_Loss无法优化两个框不相交的情况。 🍬
(2)即状态2和状态3的情况,当两个预测框大小相同,两个IOU也相同,IOU_Loss无法区分两者相交情况的不同。因此2019年出现了GIOU_Loss来进行改进。 🍬

🍀Pytorch代码:
def IoU(box1, box2):b1_x1, b1_y1, b1_x2, b1_y2 = box1b2_x1, b2_y1, b2_x2, b2_y2 = box2xx1 = np.maximum(b1_x1, b2_x1)yy1 = np.maximum(b1_y1, b2_y1)xx2 = np.minimum(b1_x2, b2_x2)yy2 = np.minimum(b1_y2, b2_y2)w = np.maximum(0.0, yy2 - yy1)h = np.maximum(0.0, xx2 - xx1)inter = w * hIoU = inter/((b1_x2-b1_x1)*(b1_y2-b1_y1) + (b2_x2-b2_x1)*(b2_y2-b2_y1) - inter)print("IoU: ", IoU)if __name__ == "__main__":box1 = np.array([100, 100, 210, 210])box2 = np.array([150, 150, 230, 220])IoU(box1, box2)🚀3.GIoU
GIOU(Generalized-IoU),GIoU比IoU多了一个“Generalized”,能在更广义的层面上计算IoU。当检测框和真实框没有出现重叠的时候IoU的loss都是一样的,因此GIoU就引入了最小封闭形状C(C可以把A,B包含在内),在不重叠情况下能让预测框尽可能朝着真实框前进,这样就可以解决检测框和真实框没有重叠的问题 。🍁
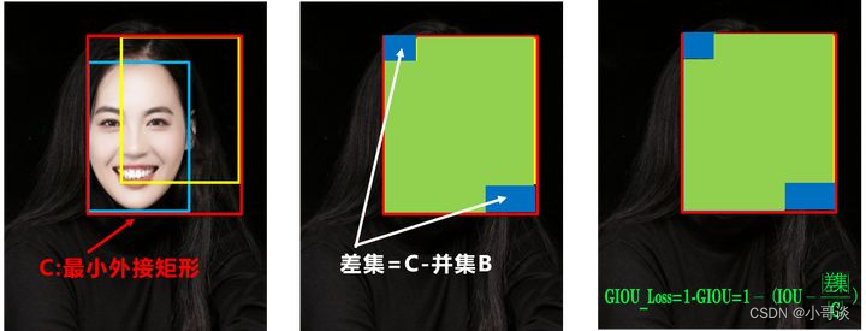
🍀计算公式:
如上图所示,GIOU在IOU的基础上,把包围矩形框A和矩形框B的最小矩形框(图中的虚线框)的面积也加入到计算中。🔖
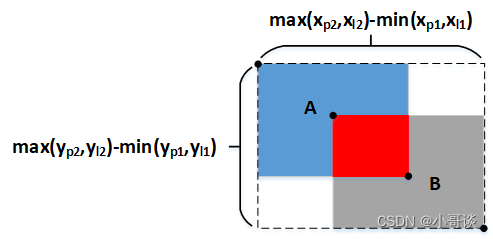
GIOU可按下式计算,其中S1为A、B相交部分的面积(红色区域)。其中S3为包围A、B的最小矩形框的面积,S2为A、B相并区域的面积(蓝色+红色+灰色区域)。🗼

由上式可知GIOU相比IOU,新增了(S3-S2)/S3这一项。新增项表示什么意义呢?❓❓❓
由上述可知S3-S2为虚线框中白色区域的面积,也即虚线框中不属于A也不属于B的空白区域,那么(S3-S2)/S3就是空白区域面积占虚线框面积的比例,这个比例越大说明A、B距离越远、重叠度越小,反之则A、B距离越近、重叠度越大。📬
GIOU的取值范围是-1~1,当A、B完全没有重叠区域时IOU为0,那么GIOU取负值,极端情况,当A、B无重叠区域且距离无限远时,此时(S3-S2)/S3等于1,那么GIOU取-1;另一个极端情况,当A、B完全重叠时(S3-S2)/S3等于0,IOU为1,那么GIOU取1。🌻
因此,GIOU解决了当A、B完全没有重叠区域时IOU恒为0的问题。
最后得到GIOU loss的计算公式:
![]()
🍀不足之处:
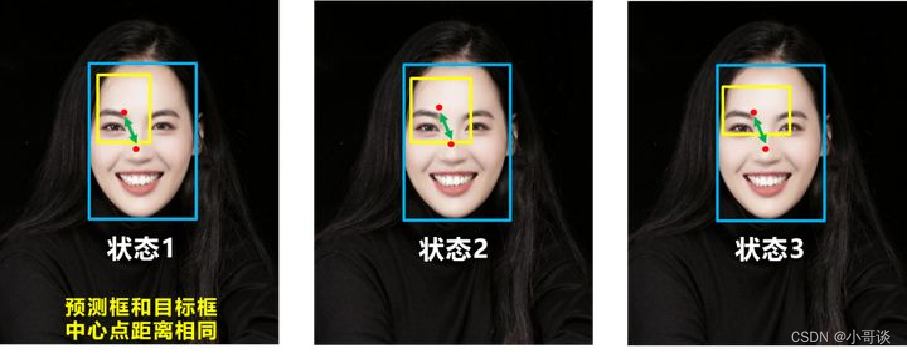
状态1、2、3都是预测框在目标框内部且预测框大小一致的情况,这时预测框和目标框的差集都是相同的,因此这三种状态的GIOU值也都是相同的,这时GIOU退化成了IOU,无法区分相对位置关系。 基于这个问题,2020年的AAAI又提出了DIOU_Loss。

🍀Pytorch代码:
def GIoU(box1, box2):b1_x1, b1_y1, b1_x2, b1_y2 = box1b2_x1, b2_y1, b2_x2, b2_y2 = box2# IOUxx1 = np.maximum(b1_x1, b2_x1)yy1 = np.maximum(b1_y1, b2_y1)xx2 = np.minimum(b1_x2, b2_x2)yy2 = np.minimum(b1_y2, b2_y2)inter_w = np.maximum(0.0, yy2 - yy1)inter_h = np.maximum(0.0, xx2 - xx1)inter = inter_w * inter_hUnion = (b1_x2-b1_x1)*(b1_y2-b1_y1) + (b2_x2-b2_x1)*(b2_y2-b2_y1) - inter# GIOUC_xx1 = np.minimum(b1_x1, b2_x1)C_yy1 = np.minimum(b1_y1, b2_y1)C_xx2 = np.maximum(b1_x2, b2_x2)C_yy2 = np.maximum(b1_y2, b2_y2)C_area = (C_xx2 - C_xx1) * (C_yy2 - C_yy1)IOU = inter / UnionGIOU = IOU - abs((C_area-Union)/C_area)print("GIOU:", GIOU)if __name__ == "__main__":box1 = np.array([100, 100, 210, 210])box2 = np.array([150, 150, 230, 220])GIoU(box1, box2)🚀4.DIoU
DIoU(Distance-IoU),考虑到GIoU的缺点,也是增加了C检测框,将真实框和预测框都包含了进来,但是DIoU计算的不是框之间的交并,而是计算的每个检测框之间的欧氏距离。DIoU要比GIou更加符合目标框回归的机制,将目标与anchor之间的距离,重叠率以及尺度都考虑进去,使得目标框回归变得更加稳定,不会像IoU和GIoU一样出现训练过程中发散等问题。🌳

🍀计算公式:
DIOU把矩形框A、B的中心点距离ρ、外接矩形框(虚线框)的对角线长度c都直接考虑进去,如下图所示:👇

DIOU可按下式计算:

由上式可知DIOU的取值范围也为-1~1,当两个框A、B完全重合时DIOU取1,当A、B距离无限远时,DIOU取-1。
从而得到DIOU loss的计算公式:
![]()
🍀不足之处:
DIoU考虑了重叠面积和中心点距离,当目标框包裹预测框的时候,直接度量2个框的距离,因此DIoU收敛的更快,但并没有考虑到长宽比。💞
🍀Pytorch代码:
def DIoU(box1, box2):b1_x1, b1_y1, b1_x2, b1_y2 = box1b2_x1, b2_y1, b2_x2, b2_y2 = box2# IOUxx1 = np.maximum(b1_x1, b2_x1)yy1 = np.maximum(b1_y1, b2_y1)xx2 = np.minimum(b1_x2, b2_x2)yy2 = np.minimum(b1_y2, b2_y2)inter_w = np.maximum(0.0, xx2 - xx1)inter_h = np.maximum(0.0, yy2 - yy1)inter = inter_w * inter_hUnion = (b1_x2 - b1_x1)*(b1_y2 - b1_y1) + (b2_x2 - b2_x1)*(b2_y2 - b2_y1) - inter# DISTANCEC_xx1 = np.minimum(b1_x1, b2_x1)C_yy1 = np.minimum(b1_y1, b2_y1)C_xx2 = np.maximum(b1_x2, b2_x2)C_yy2 = np.maximum(b1_y2, b2_y2)C_area = (C_xx2 - C_xx1) * (C_yy2 - C_yy1)center_b_x = (b1_x1+b1_x2)/2center_b_y = (b1_y1+b1_y2)/2center_gtb_x = (b2_x1+b2_x2)/2center_gtb_y = (b2_y1+b2_y2)/2center_distance = (center_gtb_x-center_b_x)**2 + (center_gtb_y-center_b_y)**2c_distance = (C_xx2 - C_xx1)**2 + (C_yy2 - C_yy1)**2IOU = inter/UnionDIOU = IOU - center_distance /c_distanceprint("DIOU:", DIOU)if __name__ == "__main__":box1 = np.array([100, 100, 210, 210])box2 = np.array([150, 150, 230, 220])DIoU(box1, box2)🚀5.CIoU
CIoU(Complete-IoU),就是在DIoU的基础上增加了检测框尺度的loss,增加了长和宽的loss,使得目标框回归更加稳定,不会像IoU和GIoU一样出现训练过程中发散等问题。💞
🍀计算公式:
CIOU Loss 和 DIOU Loss 前面的公式都是一样的,不过在此基础上还增加了一个影响因子,这样CIOU_Loss就将目标框回归函数应该考虑三个重要几何因素:重叠面积、中心点距离,长宽比全都考虑进去了。🐳

由以上可得CIOU loss的计算公式为:
![]()
🍀不足之处:
(1)如果预测框和ground truth框的长宽比是相同的,那么长宽比的惩罚项恒为0,不合理。
(2)观察CIoU中w, h相对于v的梯度,发现这两个梯度是一对相反数,也就是说,w和h不能同时增大或减小,这显然也不够合理的。
🍀Pytorch代码:
def CIoU(box1, box2):b1_x1, b1_y1, b1_x2, b1_y2 = box1b2_x1, b2_y1, b2_x2, b2_y2 = box2# IOUxx1 = np.maximum(b1_x1, b2_x1)yy1 = np.maximum(b1_y1, b2_y1)xx2 = np.minimum(b1_x2, b2_x2)yy2 = np.minimum(b1_y2, b2_y2)inter_w = np.maximum(0.0, xx2 - xx1)inter_h = np.maximum(0.0, yy2 - yy1)inter = inter_w*inter_hUnion = (b1_x2-b1_x1)*(b1_y2-b1_y1) + (b2_x2-b2_x1)*(b2_y2-b2_y1) - interIOU = inter/UnionC_xx1 = np.minimum(b1_x1, b2_x1)C_yy1 = np.minimum(b1_y1, b2_y1)C_xx2 = np.maximum(b1_x2, b2_x2)C_yy2 = np.maximum(b1_y2, b2_y2)# DISTANCEcenter_b_x = (b1_x1 + b1_x2)/2center_b_y = (b1_y1 + b1_y2)/2center_gtb_x = (b2_x1 + b2_x2)/2center_gtb_y = (b2_y1 + b2_y2)/2C_area = (C_xx2-C_xx1)*(C_yy2-C_yy1)Distance = (center_gtb_x-center_b_x)**2 + (center_gtb_y-center_b_y)**2Distance_area = Distance/C_area**2# aspect ratiopred_w = b1_y2 - b1_y1pred_h = b1_x2 - b1_x1gt_w = b2_y2 - b2_y1gt_h = b2_x2 - b2_x1v = (4/(np.pi)**2)*(np.arctan(gt_w/gt_h) - np.arctan(pred_w/pred_h))**2alpha = v/((1-IOU) + v)CIOU = IOU - Distance_area - alpha*vprint("CIOU:", CIOU)if __name__ == "__main__":box1 = np.array([100, 100, 210, 210])box2 = np.array([150, 150, 230, 220])CIoU(box1, box2)🚀6.EIoU
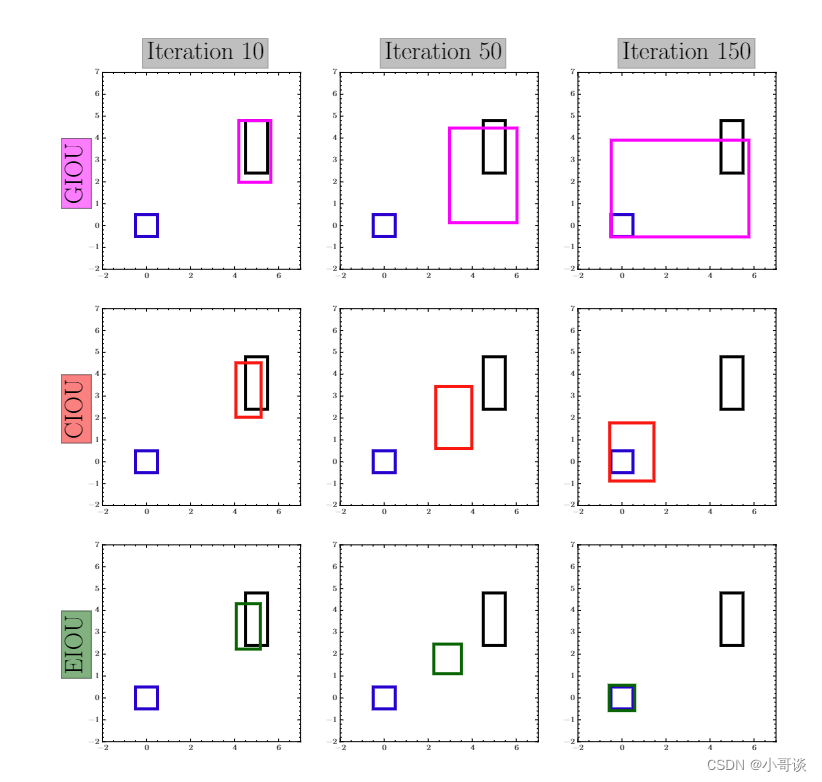
EIOU 是在 CIOU 的惩罚项基础上将预测框和真实框的纵横比的影响因子拆开,分别计算预测框和真实框的长和宽,来解决 CIOU 存在的问题。🌾
EIoU包括三个部分:IoU损失、距离损失、高宽损失(重叠面积、中心点举例、高宽比)。高宽损失直接最小化了预测目标边界框和真实边界框的高度和宽度的差异,使其有更快的收敛速度和更好的定位结果。🌾
🍀计算公式:

其中,wc和hc是预测边界框与真实边界框的最小外接矩形的宽度和高度。p是两点之间的欧氏距离。 🌴
🍀Pytorch代码:
def bbox_iou(box1, box2, x1y1x2y2=True, GIoU=False, DIoU=False, CIoU=False, EIoU=False, eps=1e-7):# Returns the IoU of box1 to box2. box1 is 4, box2 is nx4box2 = box2.T# Get the coordinates of bounding boxesif x1y1x2y2: # x1, y1, x2, y2 = box1b1_x1, b1_y1, b1_x2, b1_y2 = box1[0], box1[1], box1[2], box1[3]b2_x1, b2_y1, b2_x2, b2_y2 = box2[0], box2[1], box2[2], box2[3]else: # transform from xywh to xyxyb1_x1, b1_x2 = box1[0] - box1[2] / 2, box1[0] + box1[2] / 2b1_y1, b1_y2 = box1[1] - box1[3] / 2, box1[1] + box1[3] / 2b2_x1, b2_x2 = box2[0] - box2[2] / 2, box2[0] + box2[2] / 2b2_y1, b2_y2 = box2[1] - box2[3] / 2, box2[1] + box2[3] / 2# Intersection areainter = (torch.min(b1_x2, b2_x2) - torch.max(b1_x1, b2_x1)).clamp(0) * \(torch.min(b1_y2, b2_y2) - torch.max(b1_y1, b2_y1)).clamp(0)# Union Areaw1, h1 = b1_x2 - b1_x1, b1_y2 - b1_y1 + epsw2, h2 = b2_x2 - b2_x1, b2_y2 - b2_y1 + epsunion = w1 * h1 + w2 * h2 - inter + epsiou = inter / unionif GIoU or DIoU or CIoU or EIoU:cw = torch.max(b1_x2, b2_x2) - torch.min(b1_x1, b2_x1) # convex (smallest enclosing box) widthch = torch.max(b1_y2, b2_y2) - torch.min(b1_y1, b2_y1) # convex heightif CIoU or DIoU or EIoU: # Distance or Complete IoU https://arxiv.org/abs/1911.08287v1c2 = cw ** 2 + ch ** 2 + eps # convex diagonal squaredrho2 = ((b2_x1 + b2_x2 - b1_x1 - b1_x2) ** 2 +(b2_y1 + b2_y2 - b1_y1 - b1_y2) ** 2) / 4 # center distance squaredif DIoU:return iou - rho2 / c2 # DIoUelif CIoU: # https://github.com/Zzh-tju/DIoU-SSD-pytorch/blob/master/utils/box/box_utils.py#L47v = (4 / math.pi ** 2) * torch.pow(torch.atan(w2 / h2) - torch.atan(w1 / h1), 2)with torch.no_grad():alpha = v / (v - iou + (1 + eps))return iou - (rho2 / c2 + v * alpha) # CIoUelif EIoU:rho_w2 = ((b2_x2 - b2_x1) - (b1_x2 - b1_x1)) ** 2rho_h2 = ((b2_y2 - b2_y1) - (b1_y2 - b1_y1)) ** 2cw2 = cw ** 2 + epsch2 = ch ** 2 + epsreturn iou - (rho2 / c2 + rho_w2 / cw2 + rho_h2 / ch2)else: # GIoU https://arxiv.org/pdf/1902.09630.pdfc_area = cw * ch + eps # convex areareturn iou - (c_area - union) / c_area # GIoUelse:return iou # IoU🚀7.总结
边界框回归的三大几何因素:重叠面积、中心点距离、纵横比。🍒🍒🍒
IOU Loss:主要考虑检测框和目标框重叠面积。
GIOU Loss:在IOU的基础上,解决边界框不相交时loss等于0的问题。
DIOU Loss:在IOU和GIOU的基础上,考虑边界框中心点距离的信息。
CIOU Loss:在DIOU的基础上,考虑边界框宽高比的尺度信息。
EIOU Loss:在CIOU的基础上,解决了纵横比的模糊定义,并添加Focal Loss解决BBox回归中的样本不平衡问题。

相关文章:

YOLOv5基础知识入门(5)— 损失函数(IoU、GIoU、DIoU、CIoU和EIoU)
前言:Hello大家好,我是小哥谈。使用YOLOv5训练模型阶段,需要用到损失函数。损失函数是用来衡量模型预测值和真实值不一样的程度,极大程度上决定了模型的性能。本节就给大家介绍IoU系列损失函数,希望大家学习之后能够有…...
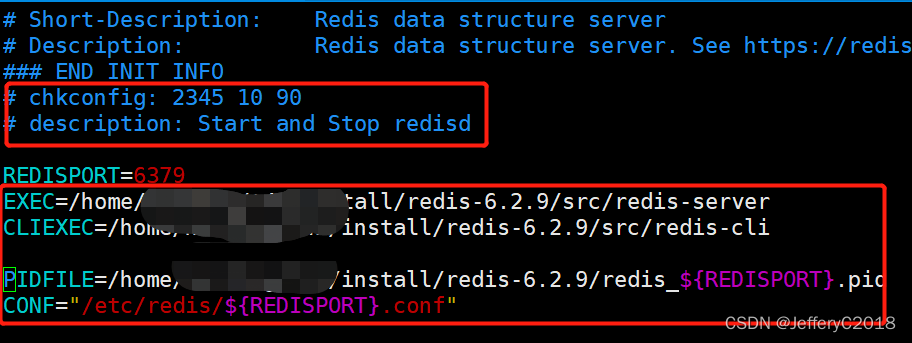
Centos7源码安装redis
1、下载redis Index of /releases/ 2、解压redis tar -xvf redis-6.2.9.tar.gz 3、进入解压后的目录 cd redis-6.2.9/4、指定内存分配器为 libc make MALLOClibc 5、进入src目录,安装 cd src && make install6、运行 ./redis-server 7、添加开机…...
[静态时序分析简明教程(九)]多周期路径set_multicycle_path
静态时序分析简明教程-多周期路径 一、写在前面1.1 快速导航链接 二、多周期路径2.1 多周期路径的SDC命令2.2 路径常规约束2.3 建立/保持规格2.4 位移量2.5 多时钟周期案例 三、总结 一、写在前面 一个数字芯片工程师的核心竞争力是什么?不同的工程师可能给出不同的…...

Unity学习笔记--使用 C# 开发一个 LRU
目录 什么是 LRULRU 核心思想代码实现一:双向链表 哈希表分析代码实现二:OrderedDictionary分析项目案例预告结尾 什么是 LRU 在计算机系统中,LRU(Least Recently Used,最近最少使用)是一种缓存置换算法。…...
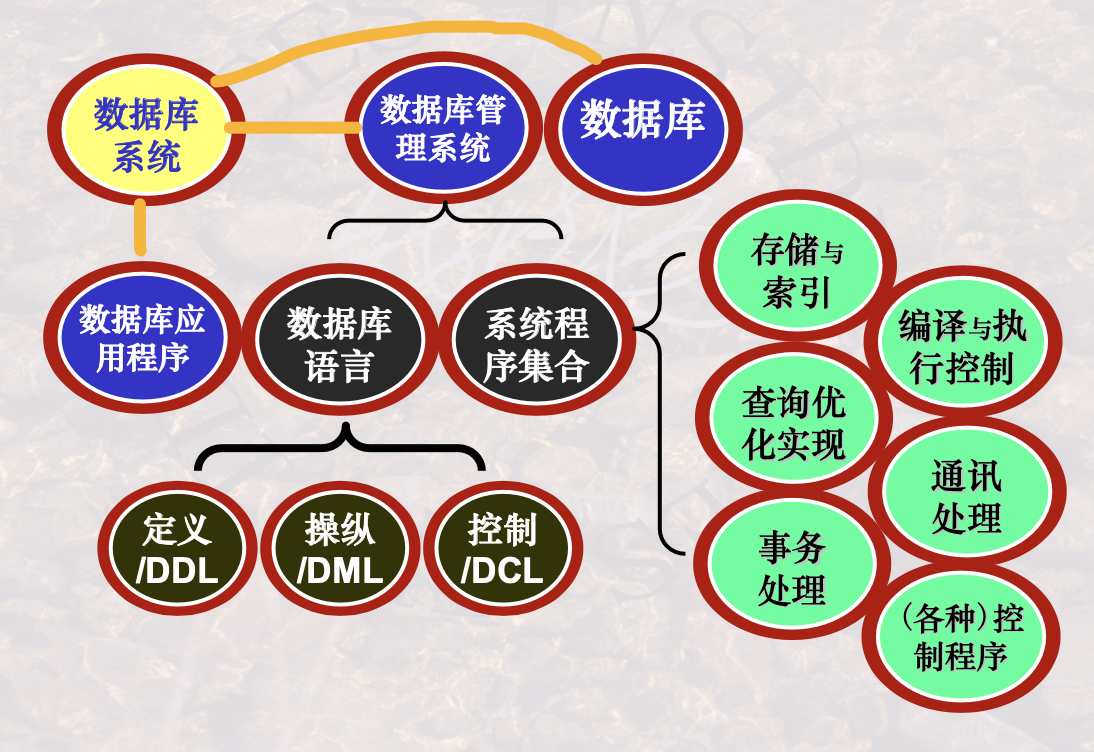
【一】初步认识数据库
数据库概览数据库 缘起表(Table)的理解用表来定义数据库数据库系统的理解概念层次的理解实例层次的理解 数据库管理系统的理解从用户角度看从系统实现角度看典型的数据库管理系统 数据库语言数据库定义、操纵、控制语言数据库语言 VS 高级语言 内容回顾练习 数据库概览 走马观…...

HTML <section> 标签
实例 文档中的区段,解释了 PRC: <section><h1>PRC</h1><p>The Peoples Republic of China was born in 1949...</p> </section>定义和用法 <section> 标签定义文档中的节(section、区段&#x…...
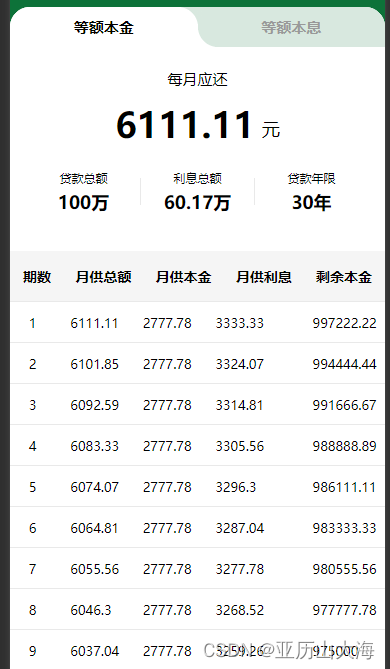
PHP 之房贷计算器、组合贷
一、等额本金 // (等额本金) //$loanAmount>贷款金额 //$loanPeriod>贷款年限 //$interestRate>贷款利息 function calculateEqualPrincipalPayment($loanAmount, $loanPeriod, $interestRate) {$monthlyPrincipal $loanAmount / ($loanPerio…...

解决Vue+Element UI使用表单rules国际化时From表单验证信息不能实时更新
说明:该篇博客是博主一字一码编写的,实属不易,请尊重原创,谢谢大家! 博主在工作之余开始进行自动化测试平台的开发,虽然已经996一个月了但是还是在使劲挤时间做这件事情,目前平台使用前端框架vu…...

友善之臂NanoPi NEO利用fbtft驱动点亮1.69寸ST7789V2屏幕
屏幕介绍 本文以中景园1.69寸LCD,驱动芯片ST7789V2该款屏幕示例,屏幕的分辨率为240*280 屏幕引脚说明 NanoPi NEO IO介绍 屏幕与板子的IO连接关系 屏幕NanoPi NEOGNDGNDVCC3.3VSCLPC2SDAPC0RESPG11DCPA1CSPC3BLKPA0 下载交叉编译器和linux内核源码并按教…...

MFC第三十天 通过CToolBar类开发文字工具栏和工具箱、GDI+边框填充以及基本图形的绘制方法、图形绘制过程的反色线模型和实色模型
文章目录 CControlBar通过CToolBar类开发文字工具栏和工具箱CMainFrame.hCAppCMainFrm.cppCMainView.hCMainView.cppCEllipse.hCEllipse.cppCLine.hCLine.cppCRRect .hCRRect .cpp CControlBar class AFX_NOVTABLE CControlBar : public CWnd{DECLARE_DYNAMIC(CControlBar)pro…...
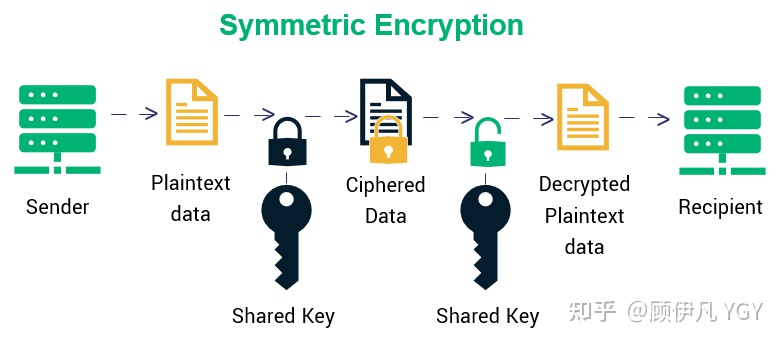
Android Https
本质:在客户端和服务端使用非对称加密协商出一套对称密钥,每次发送数据前加密,收到后解密,达到加密传输 http ssl 在http之下增加了安全层,用于保障http的加密传输 HTTPS连接 TLS连接步骤 1.客户端发送 client h…...

Games101学习笔记2
参考博客:GAMES101 梳理 / 个人向图形学笔记_games101笔记_river_of_sebajun的博客-CSDN博客 lecture 05 Rasterization 1(Triangles) 光栅化 把东西画在屏幕上的过程就是光栅化的过程 视口变换 为什么模型用三角形? 最基本的几何平面;保…...

java字符串String类的常用方法
java字符串String类的常用方法 字符串的创建: (1)定义字符串直接赋值,在字符串池中开辟空间() String str1“Hello”;//在字符串池中写入字符串"hello" String str2“Hello”;//直接引用字符串池中的"Hello" System.out.println(s…...

自动化测试如何解决chrome自动更新问题
问题 调试好的自动化测试脚本,有时候总是在第一天或过几天就不好使了。产品并未进行功能逻辑,ui修改,一切还和调试自动化脚本的时候保持一致。运行自动化测试脚本时,控制台总是会在driver webdriver.Chrome()这一行报错。 问题…...

闲鱼卖货:新手容易踩坑的7个地方。赶紧看看有没有中招?
科思创业汇 大家好,这里是科思创业汇,一个轻资产创业孵化平台。赚钱的方式有很多种,我希望在科思创业汇能够给你带来最快乐的那一种! 这是我以前的一个学生收到的第一个非法通知。他告诉我,他当时很害怕,…...

PowerShell 获取某目录下所有的文件、文件夹,同时对获取到的文件路径字符串进行替换处理
PowerShell 获取某目录下所有的文件、文件夹,同时对获取到的文件路径字符串进行替换处理 前言: 为了将Windows系统下的Java编译文件与linux服务器上的文件进行比较,故进行此文件路径的获取及路径处理。 在只有文件路径 而没有实际文件的情况下…...
JUC并发编程之线程锁(一)
目录 1.ReentrantLock(互斥锁) 2.ReentRantReaderWriterLock(互斥读写锁) 3.StampedLock(无障碍锁) 4.Condition(自定义锁) 5.LockSupport 问题引出: 由于传统的线程控制需要用到同步机制Sy…...

Android AlertDialog标题居中
网上很多做法都是使用setCustomTitle方法实现的,我偏不,因为我已经找到了标题的textView了: 在show了之后可以拿到标题(注意一定是show之后才能拿得到,create之后拿也是空的): TextView title…...

k8s界面化平台dashboard、kubesphere、Rancher对比
k8s集群管理dashboard有很多,比如kuboard、官方发dashboard、kubesphere、Rancher等等。 Dashboard、KubeSphere 和 Rancher 都是流行的 Kubernetes 管理和操作界面。它们都提供了图形化的用户界面,以简化对 Kubernetes 集群的管理和监控。每个工具都有其…...

【字符串左旋】
字符串左旋 1.题目要求 实现一个函数,可以左旋字符串中的k个字符。 例如: ABCD左旋一个字符得到BCDA ABCD左旋两个字符得到CDAB 2.解法: 设计循环使其可以旋1次,然后让他执行n次是一个最简单的思路: 函数实现…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...
