LeetCode 2811. Check if it is Possible to Split Array【脑筋急转弯;前缀和+动态规划或记忆化DFS】中等
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章中,我不仅会讲解多种解题思路及其优化,还会用多种编程语言实现题解,涉及到通用解法时更将归纳总结出相应的算法模板。
为了方便在PC上运行调试、分享代码文件,我还建立了相关的仓库:https://github.com/memcpy0/LeetCode-Conquest。在这一仓库中,你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等,还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解,还可以一同分享给他人。
由于本系列文章的内容随时可能发生更新变动,欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。
给你一个长度为 n 的数组 nums 和一个整数 m 。请你判断能否执行一系列操作,将数组拆分成 n 个 非空 数组。
在每一步操作中,你可以选择一个 长度至少为 2 的现有数组(之前步骤的结果) 并将其拆分成 2 个子数组,而得到的 每个 子数组,至少 需要满足以下条件之一:
- 子数组的长度为 1 ,或者
- 子数组元素之和 大于或等于
m。
如果你可以将给定数组拆分成 n 个满足要求的数组,返回 true ;否则,返回 false 。
注意: 子数组是数组中的一个连续非空元素序列。
示例 1:
输入:nums = [2, 2, 1], m = 4
输出:true
解释:
第 1 步,将数组 nums 拆分成 [2, 2] 和 [1] 。
第 2 步,将数组 [2, 2] 拆分成 [2] 和 [2] 。
因此,答案为 true 。
示例 2:
输入:nums = [2, 1, 3], m = 5
输出:false
解释:
存在两种不同的拆分方法:
第 1 种,将数组 nums 拆分成 [2, 1] 和 [3] 。
第 2 种,将数组 nums 拆分成 [2] 和 [1, 3] 。
然而,这两种方法都不满足题意。因此,答案为 false 。
示例 3:
输入:nums = [2, 3, 3, 2, 3], m = 6
输出:true
解释:
第 1 步,将数组 nums 拆分成 [2, 3, 3, 2] 和 [3] 。
第 2 步,将数组 [2, 3, 3, 2] 拆分成 [2, 3, 3] 和 [2] 。
第 3 步,将数组 [2, 3, 3] 拆分成 [2] 和 [3, 3] 。
第 4 步,将数组 [3, 3] 拆分成 [3] 和 [3] 。
因此,答案为 true 。
提示:
1 <= n == nums.length <= 1001 <= nums[i] <= 1001 <= m <= 200
解法1 记忆化DFS/区间DP+前缀和
为了方便求出子数组的和,我们使用前缀和。
对于数组拆分,很自然地想到DFS,但如果每次都在数组两侧拆分,则复杂度可能到 O ( 2 100 ) O(2^{100}) O(2100) ,为此必须使用记忆化+DFS。我个人的写法如下所示,令 d f s ( l , r ) dfs(l, r) dfs(l,r) 表示区间 [ l , r ] [l,r] [l,r] 可否拆分:
- 递归边界:区间长度 ≤ 2 \le 2 ≤2 ,一定可拆分;在区间长度 > 2 > 2 >2 且区间和 ≤ m \le m ≤m 时,此时无论如何都无法继续拆分下去。
- 递归过程:只有区间和大于 m m m 且可以拆分出子区间 [ l + 1 , r ] [l + 1, r] [l+1,r] 或 [ l , r − 1 ] [l, r - 1] [l,r−1](对应区间长度为 1 1 1 或区间和 ≥ m \ge m ≥m ),且满足子区间可拆分——即 d f s ( l + 1 , r ) = t r u e dfs(l + 1, r) = true dfs(l+1,r)=true 或 d f s ( l , r − 1 ) = t r u e dfs(l, r - 1)= true dfs(l,r−1)=true ,此时区间 [ l , r ] [l, r] [l,r] 可以拆分。
class Solution {
private:int m;int sum[110];int dp[110][110];int dfs(int l, int r) {if (dp[l][r] != -1) return dp[l][r]; // 已经有答案if (l + 1 >= r) return dp[l][r] = 1; // 拆分前进行判断,可以拆分if (sum[r + 1] - sum[l] <= m) return dp[l][r] = 0; // 拆分前进行判断,不可拆分int left = 0, right = 0;if (l + 1 == r || sum[r + 1] - sum[l + 1] >= m) // 看是否可以拆分出[l+1,r]这个子数组left = dfs(l + 1, r); // 看[l+1,r]子数组是否可继续拆分if (l == r - 1 || sum[r] - sum[l] >= m) // 看是否可以拆分出[l,r-1]这个子数组right = dfs(l, r - 1); // 看[l,r-1]子数组是否可继续拆分return dp[l][r] = left || right; }
public:bool canSplitArray(vector<int>& nums, int m) {this->m = m;memset(sum, 0, sizeof(sum));memset(dp, -1, sizeof(dp));int n = nums.size();for (int i = 0; i < n; ++i) sum[i + 1] = sum[i] + nums[i];return dfs(0, n - 1);}
};
还可使用区间DP:
class Solution {
public:bool canSplitArray(vector<int>& nums, int m) {int sum[110];bool dp[110][110];memset(sum, 0, sizeof(sum));memset(dp, false, sizeof(dp));int n = nums.size();for (int i = 0; i < n; ++i) sum[i + 1] = sum[i] + nums[i];// dp[i][j]表示区间[i,j]能否拆分for (int i = n - 1; i >= 0; --i) {dp[i][i] = true;if (i + 1 < n) dp[i][i + 1] = true;// 区间[i,j-1], [i+1,j]是否可拆for (int j = i + 2; j < n; ++j) {// [i,j]能否拆分为[i+1,j]或[i,j-1],看拆出子数组的和是否>=m,且拆出子数组是否可继续拆分if (sum[j] - sum[i] >= m && dp[i][j - 1]|| sum[j + 1] - sum[i + 1] >= m && dp[i + 1][j])dp[i][j] = true; }}return dp[0][n - 1];}
};
解法2 脑筋急转弯(最优解法)
要善于将题目转换成另外一种解法,对题目的理解、数学逻辑要求较高。
- 先特判 n ≤ 2 n \le 2 n≤2 的情况,这是满足要求的。
- 对于 n ≥ 3 n\ge 3 n≥3 的情况,无论按照何种方式分割,一定会在某个时刻,分割出一个长为 2 2 2 的子数组。
- 如果 nums \textit{nums} nums 中任何长为 2 2 2 的子数组的元素和都小于 m m m ,那么无法满足要求。
- 否则,可以用这个子数组作为「核心」,像剥洋葱一样,一个一个地去掉 nums \textit{nums} nums 的首尾元素,最后得到这个子数组。由于子数组的元素和 ≥ m \ge m ≥m ,所以每次分割出一个元素时,剩余的子数组的元素和也必然是 ≥ m \ge m ≥m 的,满足要求。
于是本题可转换成:求数组中是否存在2个相邻元素之和 ≥ m \ge m ≥m 。相信题目如果这么问,100%的人都能做出来。
class Solution {
public:bool canSplitArray(vector<int>& nums, int m) {int n = nums.size();for (int i = 1; i < n; ++i)if (nums[i - 1] + nums[i] >= m) return true;return n <= 2;}
};
相关文章:

LeetCode 2811. Check if it is Possible to Split Array【脑筋急转弯;前缀和+动态规划或记忆化DFS】中等
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...

【学习日记】【FreeRTOS】链表结构体及函数详解
写在前面 本文主要是对于 FreeRTOS 中链表相关内容的详细解释,代码大部分参考了野火FreeRTOS教程配套源码,作了一小部分修改。 一、结构体定义 主要包含三种结构体: 普通节点结构体结尾节点(mini节点)结构体链表结…...
【云原生•监控】基于Prometheus实现自定义指标弹性伸缩(HPA)
【云原生•监控】基于Prometheus实现自定义指标弹性伸缩(HPA) 什么是弹性伸缩 「Autoscaling即弹性伸缩,是Kubernetes中的一种非常核心的功能,它可以根据给定的指标(例如 CPU 或内存)自动缩放Pod副本,从而可以更好地管…...

Windows、 Linux 等操作系统的基本概念及其常见操作
Windows 和 Linux 是两种常见的操作系统,它们在计算机领域中广泛使用。下面我将为您介绍它们的基本概念以及一些常见的操作。 **Windows 操作系统:** 1. **基本概念:** Windows 是由微软公司开发的操作系统系列,旨在为个人计算机…...
【RabbitMQ】golang客户端教程5——使用topic交换器
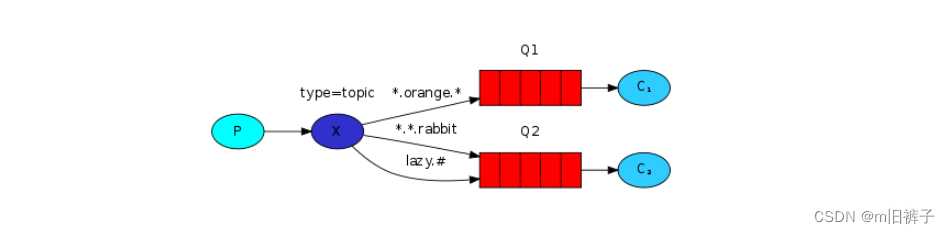
topic交换器(主题交换器) 发送到topic交换器的消息不能具有随意的routing_key——它必须是单词列表,以点分隔。这些词可以是任何东西,但通常它们指定与消息相关的某些功能。一些有效的routing_key示例:“stock.usd.ny…...

SpringBoot对接OpenAI
SpringBoot对接OpenAI 随着人工智能技术的飞速发展,越来越多的开发者希望将智能功能集成到自己的应用中,以提升用户体验和应用的功能。OpenAI作为一家领先的人工智能公司,提供了许多先进的自然语言处理和语言生成模型,其中包括深…...

(C++)继承
目录 1.继承的概念及定义 1.1继承的概念 1.2继承定义 1.2.1定义格式 1.2.2继承方式和访问限定符 1.2.3继承基类成员访问方式的变化 2.基类和派生类对象赋值转换 3.继承中的作用域 4.派生类的默认成员函数 5.继承与友元 6.继承与静态成员 7.复杂的菱形继承及菱形虚拟…...

图像处理技巧形态学滤波之膨胀操作
1. 引言 欢迎回来,我的图像处理爱好者们!今天,让我们继续研究图像处理领域中的形态学计算。在本篇中,我们将重点介绍腐蚀操作的反向效果膨胀操作。 闲话少说,我们直接开始吧! 2. 膨胀操作原理 膨胀操作…...

机器学习基础之《特征工程(4)—特征降维》
一、什么是特征降维 降维是指在某些限定条件下,降低随机变量(特征)个数,得到一组“不相关”主变量的过程 1、降维 降低维度 ndarry 维数:嵌套的层数 0维:标量,具体的数0 1 2 3... …...
)
学生管理系统(Python版本)
class Student:def __init__(self, id, name, age):self.id idself.name nameself.age ageclass StudentManagementSystem:def __init__(self):self.students []def add_student(self, student):self.students.append(student)print("学生信息添加成功!&qu…...

Linux下快速创建大文件的4种方法总结
1、使用 dd 命令创建大文件 dd 命令用于复制和转换文件,它最常见的用途是创建实时 Linux USB。dd 命令是实际写入硬盘,文件产生的速度取决于硬盘的读写速度,根据文件的大小,该命令将需要一些时间才能完成。 假设我们要创建一个名…...

用 Rufus 制作 Ubuntu 系统启动盘时,选择分区类型为MBR还是GPT?
当使用 Rufus 制作 Ubuntu 系统启动盘时,您可以根据您的需求选择分区类型,MBR(Master Boot Record)还是 GPT(GUID Partition Table)。 MBR 是传统的分区表格式,适用于大多数旧版本的操作系统和旧…...
Nodejs+vue+elementui汽车租赁管理系统_1ma2x
语言 node.js 框架:Express 前端:Vue.js 数据库:mysql 数据库工具:Navicat 开发软件:VScode 前端nodejsvueelementui, 课题主要分为三大模块:即管理员模块、用户模块和普通管理员模块,主要功能包括&#…...
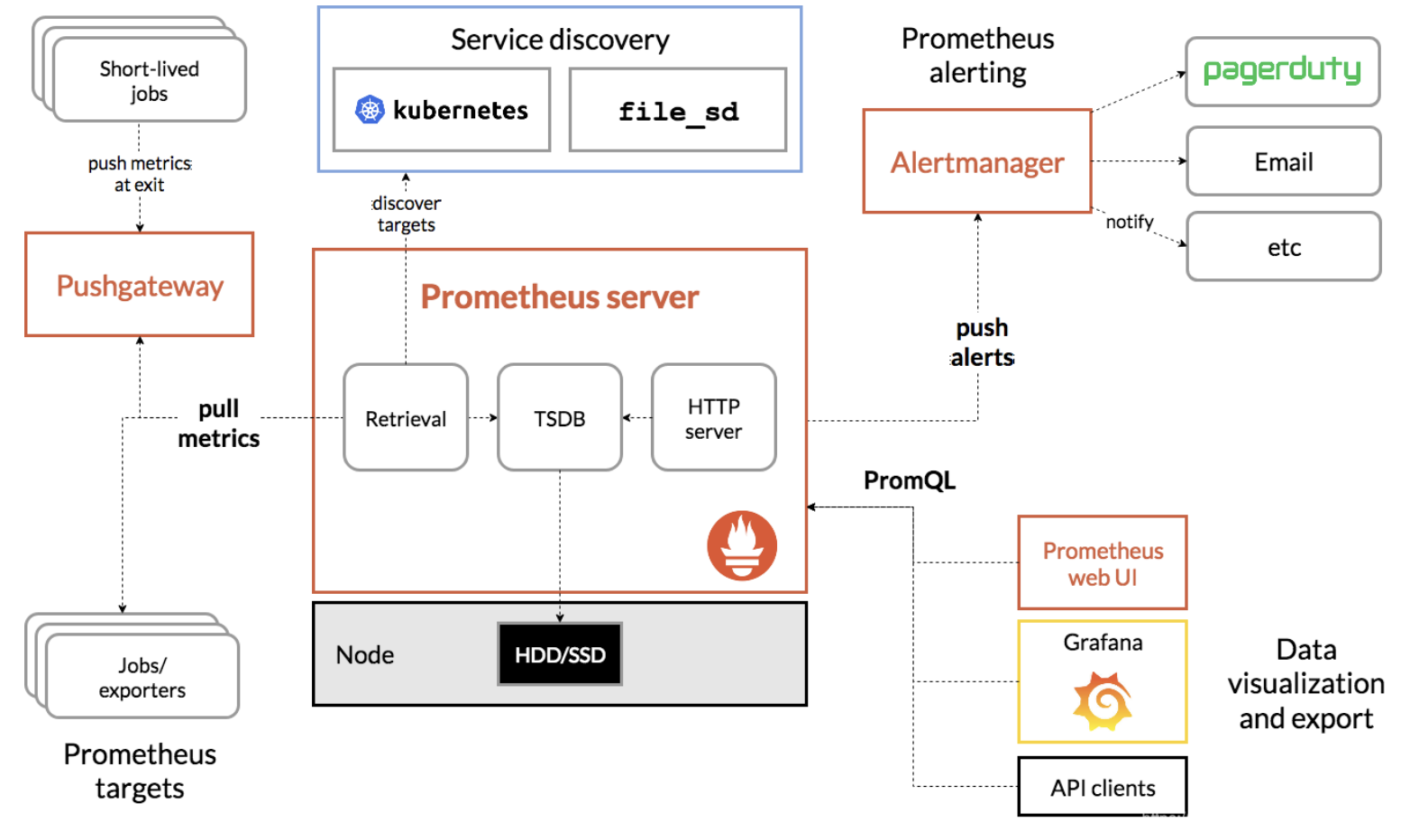
Prometheus入门
Prometheus(普罗米修斯) 是一种 新型监控告警工具,Kubernetes 的流行带动了 Prometheus 的应用。 全文参考自 prometheus 学习笔记(1)-mac 单机版环境搭建[1] Mac 上安装 Prometheus brew install prometheus 安装路径在 /usr/local/Cellar/prometheus/2.20.1, 配置文件在 /usr…...

RISC-V云测平台:Compiling The Fedora Linux Kernel Natively on RISC-V
注释:编译Fedora,HS-2 64核RISC-V服务器比Ryzen5700x快两倍! --- 以下是blog 正文 --- # Compiling The Fedora Linux Kernel Natively on RISC-V ## Fedora RISC-V Support There is ongoing work to Fedora to support RISC-V hardwar…...

Vim学习(三)—— Git Repo Gerrit
Git、Gerrit、Repo三者的概念及使用 三者各自作用: git:版本管理库,在git库中没有中心服务器的概念,真正的分布式。 repo:repo就是多个git库的管理工具。如果是多个git库同时管理,可以使用repo。当然使用…...

论坛项目之用户部分
注册接口 实现思路 1.特殊字段检查(比如性别没有给出需要给出默认值) 2.对比检查两次输入的密码是否一致,不一致报错 3.利用UUID生成随机‘盐’值,并使用密码进行MD5加密后与‘盐’进行拼接,生成加密后的密码 4.创建U…...

golang内存对齐
为什么要内存对齐? CPU访问内存时,以CPU的位数为单位进行访问。 如果访问未对齐的内存,处理器需要做两次内存访问,对齐的内存的访问可能仅需要一次,利用内存对齐后提升读取速度。 golang结构体内存对齐规则 在代码编译…...

【CheatSheet】Python、R、Julia数据科学编程极简入门
《Python、R、Julia数据科学编程极简入门》PDF版,是我和小伙伴一起整理的备忘清单,帮助大家10分钟快速入门数据科学编程。 另外,最近 TIOBE 公布了 2023 年 8 月的编程语言排行榜。 Julia 在本月榜单中实现历史性突破,成功跻身 …...
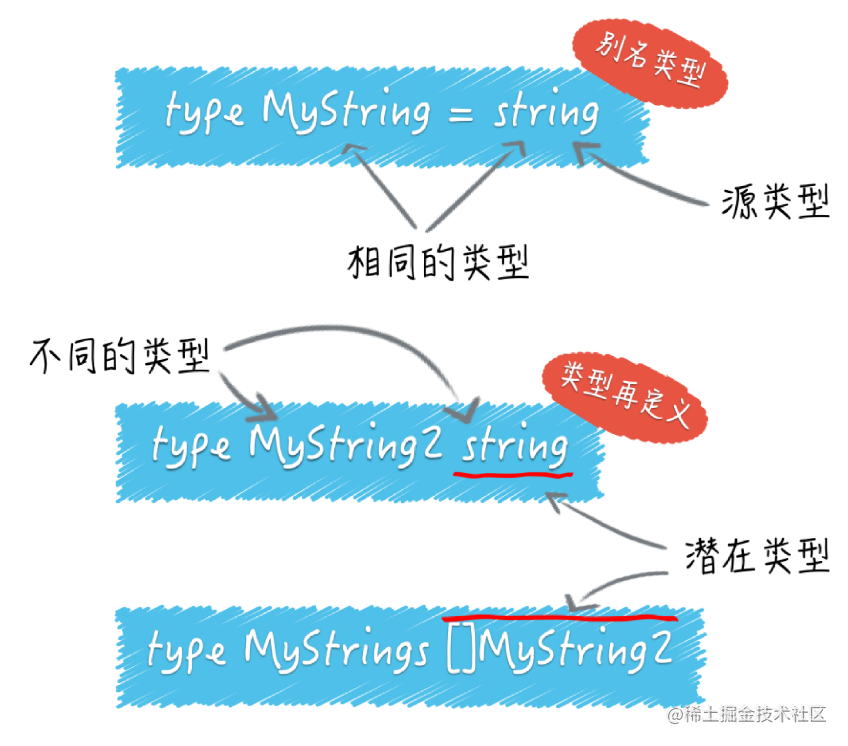
【golang】怎样判断一个变量的类型?
怎样判断一个变量的类型? package mainimport "fmt"var container []string{"zero", "one", "two"} func main() {container : map[int]string{0: "zero", 1: "one", 2: "two"}fmt.Printf…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...

沙箱虚拟化技术虚拟机容器之间的关系详解
问题 沙箱、虚拟化、容器三者分开一一介绍的话我知道他们各自都是什么东西,但是如果把三者放在一起,它们之间到底什么关系?又有什么联系呢?我不是很明白!!! 就比如说: 沙箱&#…...
