2.0 Maven基础
1. Maven概述
Maven概念
Apache Maven是一个软件项目管理工具,将项目开发和管理过程抽象程一个项目对象模型(POM,Project Object Model)。
Maven作用
-
项目构建
提供标准的、跨平台的自动化项目构建方式。
-
依赖管理
方便快捷的管理项目依赖的资源(jar包),避免资源间的版本冲突。
-
统一开发结构
提供标准的、统一的项目结构。
Maven坐标
Maven中的坐标用于描述仓库中资源的位置。
-
Maven坐标组成
groupId:定义当前Maven项目隶属组织名称
artifactId:定义当前Maven项目名称
version:定义当前项目版本号
-
Maven坐标作用
使用唯一标识,唯一性定位资源位置,通过该标识可以将资源的识别与下载工作交由Maven完成。
Maven仓库
用于存储资源,包含各种jar包,可分为中央仓库、私服和本地仓库。
-
中央仓库
Maven团队维护,为本地仓库提供资源。
-
私服
公司范围内存储资源的仓库,可以从中央仓库获取资源,也有自主研发的资源。
-
本地仓库
自己电脑上存储资源的仓库,连接中央仓库或者私服获取资源。
Maven Repository
https://mvnrepository.com/
2. Maven安装与配置
Maven下载
Maven – Download Apache Maven
Maven版本
apache-maven-3.6.3
Maven配置
-
配置Java环境
Maven是Java开发的,需要配置JAVA_HOME。
-
配置Maven本地仓库
编辑apache-maven-3.6.3\conf\settings.xml文件,设置
<localRepository>D:\maven\repository</localRepository>-
配置Maven阿里云镜像
编辑apache-maven-3.6.3\conf\settings.xml文件,设置mirrors。
<mirrors><mirror><id>nexus-aliyun</id><mirrorOf>central</mirrorOf><name>Nexus aliyun</name><url>http://maven.aliyun.com/nexus/content/groups/public</url></mirror>
</mirrors>3. Maven入门案例
IDEA集成Maven
-
打开Maven设置
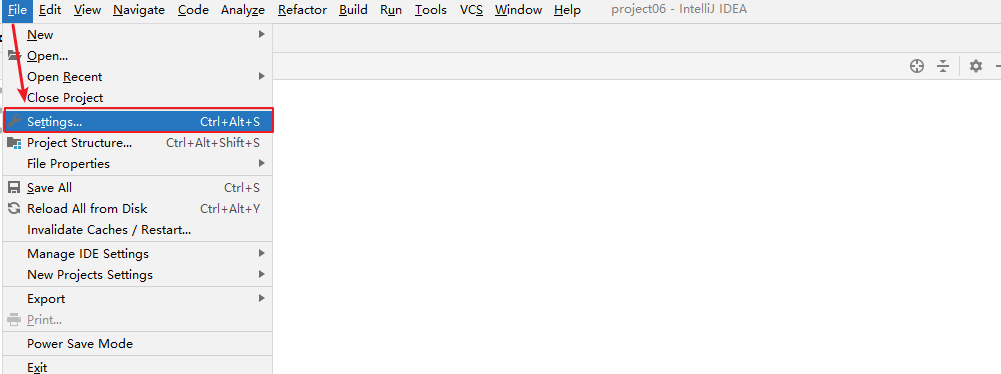
-
设置Maven
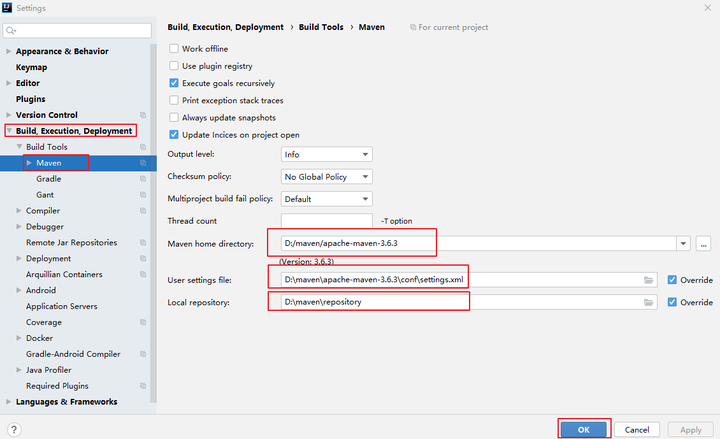
4. Maven入门案例
基于Maven构建快速构建项目,输出“Hello World!”。
案例实现详见链接:案例10 Maven入门案例
5. 基于Maven构建实现学生新增案例
基于Maven快速构建,实现学生新增。
案例实现详见链接:案例11 基于Maven构建实现学生新增案例
相关文章:

2.0 Maven基础
1. Maven概述 Maven概念 Apache Maven是一个软件项目管理工具,将项目开发和管理过程抽象程一个项目对象模型(POM,Project Object Model)。 Maven作用 项目构建 提供标准的、跨平台的自动化项目构建方式。 依赖管理 方便快捷…...
在Linux虚拟机内配置nginx以及docker
目录 1、nginx源码包编译以及安装依赖 1、配置安装所需的编译环境 2、安装函数库(pcre、zlib、openssl) 2、安装nginx 1、获取源码包 2、解压编译 3、启动nginx服务 1、关闭防火墙 2、运行nginx 3、使用本地浏览器进行验证 3、安装docker 1、…...

数据结构-带头双向循环链表的实现
前言 带头双向循环链表是一种重要的数据结构,它的结构是很完美的,它弥补了单链表的许多不足,让我们一起来了解一下它是如何实现的吧! 1.节点的结构 它的节点中存储着数据和两个指针,一个指针_prev用来记录前一个节点…...
android Ndk Jni动态注册方式以及静态注册
目录 一.静态注册方式 二.动态注册方式 三.源代码 一.静态注册方式 1.项目名\app\src\main下新建一个jni目录 2.在jni目录下,再新建一个Android.mk文件 写入以下配置 LOCAL_PATH := $(call my-dir)//获取当前Android.mk所在目录 inclu...
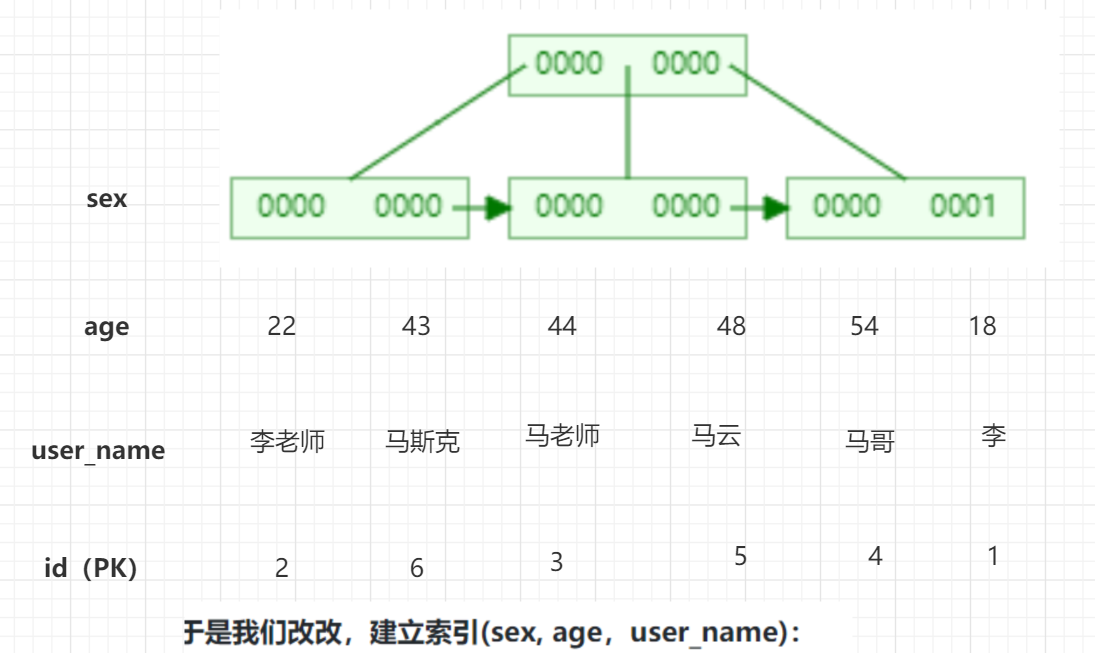
MySQL中的索引
1.2.MySQL中的索引 InnoDB存储引擎支持以下几种常见的索引:B树索引、全文索引、哈希索引,其中比较关键的是B树索引 1.2.1.B树索引 InnoDB中的索引自然也是按照B树来组织的,前面我们说过B树的叶子节点用来放数据的,但是放什么数…...
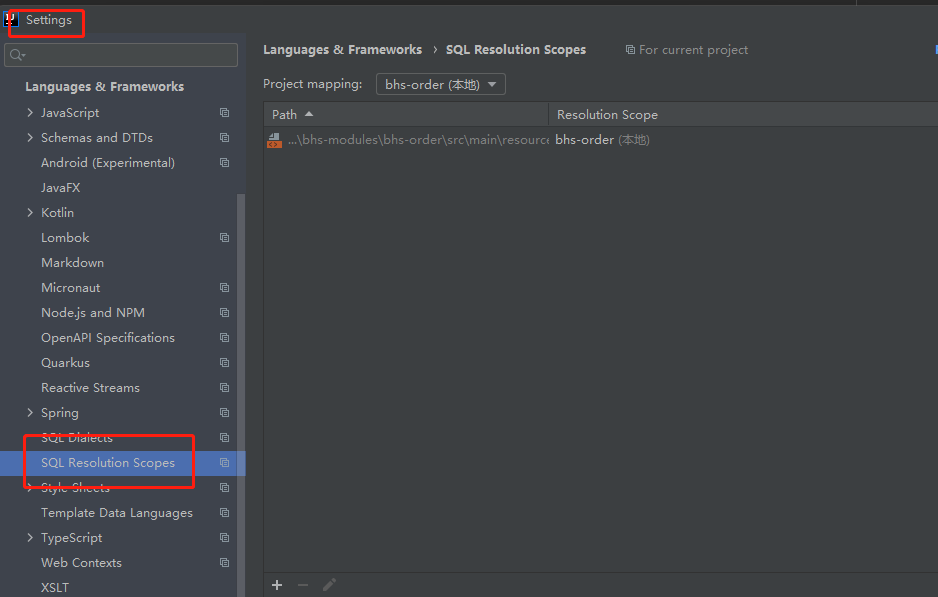
idea中如何处理飘红提示
idea中如何处理飘红提示 在写sql时,总是会提示各种错误 查找资料,大部分都是说关提示,这里把错误提示选择为None即可 关掉以后,也确实不显示任何提示了,但总有一种掩耳盗铃的感觉 这个sms表明明存在,但是还…...

Elasticsearch使用中出现的错误
Elasticsearch使用中出现的错误 1、分页查询异常 在分页的过程中出现了一个问题是当查询的数据超过10000条的时候报了异常: from size must be less than or equal to: [10000]这个问题最快捷的解决方式是增大窗口大小: curl -XPUT http://127.0.0.…...
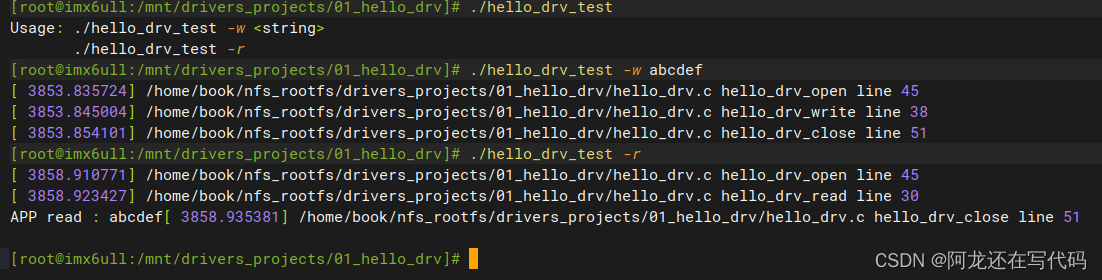
【IMX6ULL驱动开发学习】01.编写第一个hello驱动+自动创建设备节点(不涉及硬件操作)
目录 一、驱动程序编写流程 二、代码编写 2.1 驱动程序hello_drv.c 2.2 测试程序 2.3 编写驱动程序的Makefile 三、上机实验 3.1 NFS 挂载 3.2 测试示例 一、驱动程序编写流程 构造file_operations结构体 在里面填充open/read/write/ioctl成员 注册file_operations结…...

决策规划仿真平台搭建
决策规划仿真平台搭建 自动驾驶决策规划算法第二章第一节 决策规划仿真平台搭建 这部分的主要难点在于多个软件的连通与适配,环境的搭建总是折磨人的,主要是 4 个软件,各软件版本如下 Visual Studio2017PreScan8.5.0CarSim2019.0MATLAB2019b…...

计算图像哈希SHA-512
1、MATLAB实现 计算图像哈希值SHA-512,在文献[1]提到的算法如下: % Example Code: Create an MD5 crypto-hash of an arbitrary string, "str" % Main class of interest: System.Security.Cryptography.HashAlgorithm% Example String to hash with MD5 %…...
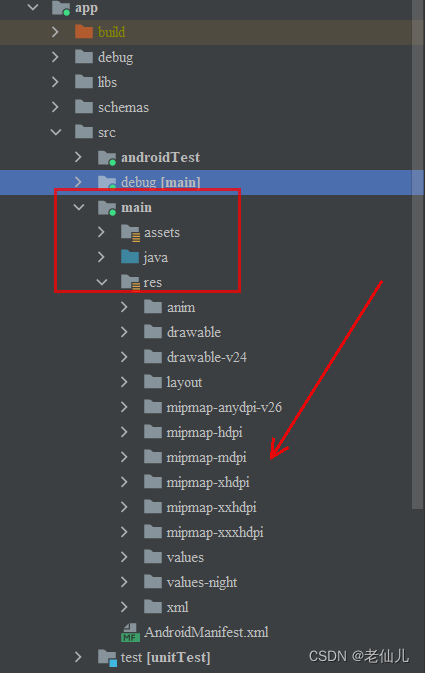
Android之消除APP图标的白色边框
有问题的效果: 解决方案: 第一步:app右键—>new—>Image Asset 第二步:上传Logo图标,选择每种分辨率,预览看效果,选择Resize,可以微调 第三步:点击 Nextÿ…...
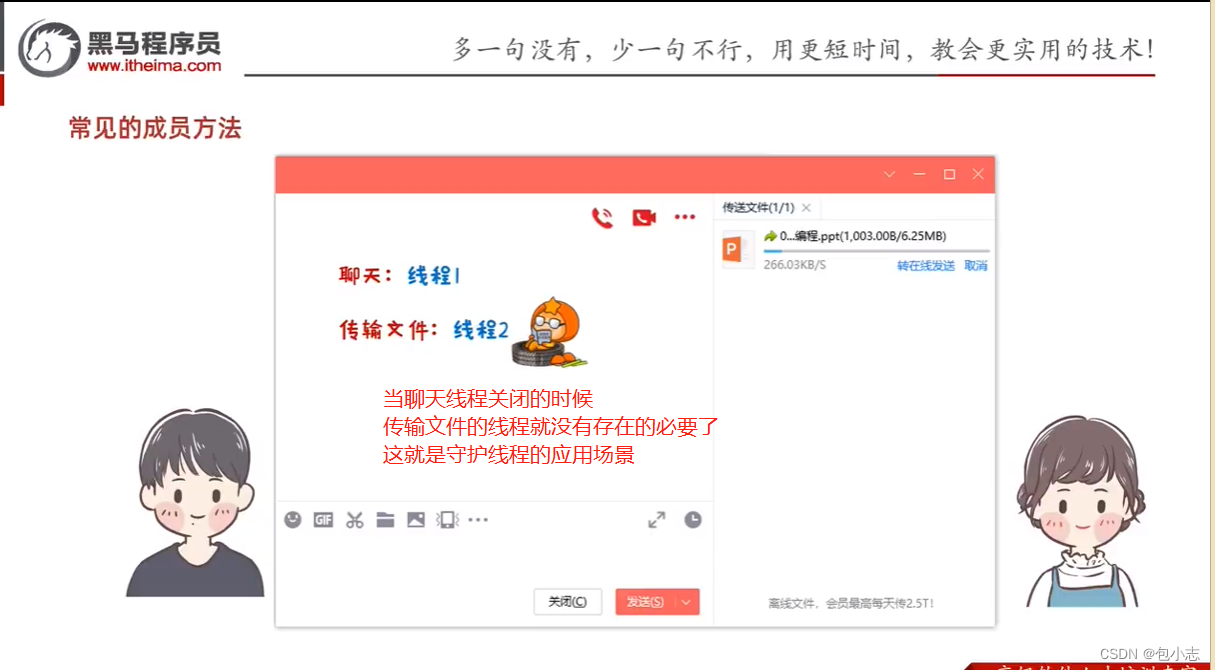
java线程的优先级、守护线程的概念
1.线程的调度 抢占式调度 非抢占式调度 1.1 抢占式调度 优先级越高,抢到cpu的概率越高 1.2 守护线程 守护线程,非守护线程。当其他的非守护线程执行完毕以后,守护线程会陆续结束。 守护线程的应用场景...

asp.net core 6.0 efcore +sqlserver增删改查的demo
asp.net core 6.0 efcore sqlserver增删改查的demo 下面是一个使用ASP.NET Core 5.0和Entity Framework Core进行增删改查操作的示例。 首先,创建一个空的ASP.NET Core 6.0 Web应用程序项目。 然后,安装以下NuGet包: Microsoft.EntityFra…...

HC32L110B6芯片测试
到货之后,直观上感觉的确很小,小包装盒里面还装了说明书。 下载器单独在一个盒里面,但是这个T-U2T没用上,还是用的STLINK。 开发之前先去网上找了一些别人遇到的坑,的确不少。 涉及的方面也是挺全的,供电、…...

关于我乱删注册表导致电脑没有声音这件事
之前因为想彻底删除迅雷,照着网上进入注册表一顿乱删,也忘记删了啥,反正把一顿xmp的文件,和搜索出来迅雷的全删了。结果迅雷确实没了,被带走的还有电脑的声音。 很离谱,就试过了所有方法都没用,…...

Linux 命令 su 和 sudo 的区别
之前一直对 su 和 sudo 这两个命令犯迷糊,最近专门搜了这方面的资料,总算是把两者的关系以及用法搞清楚了,这篇文章来系统总结一下。 1. 准备工作 因为本篇博客中涉及到用户切换,所以我需要提前准备好几个测试用户,方…...

微信小程序:Mobx的使用指南
简要 微信小程序中有时需要进行全局状态管理,这个时候就需要用到Mobx.下面我们来看一下在小程序中是如何使用Mobx的 安装 pnpm i mobx-miniprogram4.13.2 mobx-miniprogram-bindings1.2.1 或 npm i mobx-miniprogram4.13.2 mobx-miniprogram-bindings1.2.1 或 yarn…...
【Spring Boot】Spring Boot项目的创建和文件配置
目录 一、为什么要学Spring Boot 1、Spring Boot的优点 二、创建Spring Boot项目 1、创建项目之前的准备工作 2、创建Spring Boot项目 3、项目目录的介绍 4、安装Spring Boot快速添加依赖的插件 5、在项目中写一个helloworld 三、Spring Boot的配置文件 1、配置文件的…...
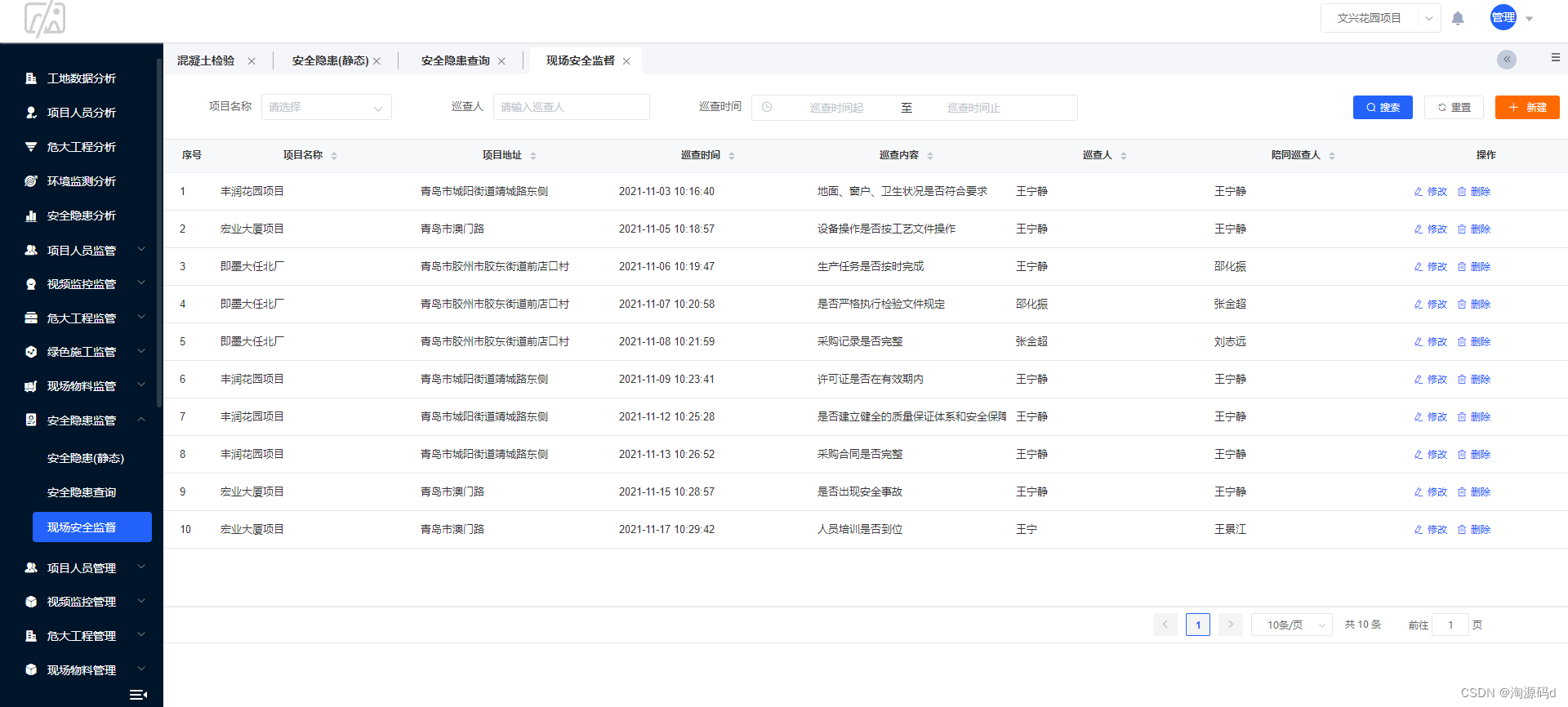
Spring Cloud 智慧工地源码(PC端+移动端)项目平台、监管平台、大数据平台
智慧工地源码 智慧工地云平台源码 智慧建筑源码 “智慧工地”是利用物联网、人工智能、云计算、大数据、移动互联网等新一代信息技术,彻底改变传统建筑施工现场参建各方现场管理的交互方式、工作方式和管理模式,实现对人、机、料、法、环的全方位实时监…...
通达OA SQL注入漏洞【CVE-2023-4165】
通达OA SQL注入漏洞【CVE-2023-4165】 一、产品简介二、漏洞概述三、影响范围四、复现环境POC小龙POC检测工具: 五、修复建议 免责声明:请勿利用文章内的相关技术从事非法测试,由于传播、利用此文所提供的信息或者工具而造成的任何直接或者间接的后果及损…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...
