数字图像处理 --- 相机的内参与外参(CV学习笔记)
Pinhole Camera Model(针孔相机模型)
针孔相机是一种没有镜头、只有一个小光圈的简单相机。 光线穿过光圈并在相机的另一侧呈现倒立的图像。为了建模方便,我们可以把物理成像平面(image plane)上的图像移到实际场景(3D object)和焦点(focal point)之间,把他想象成一个和物理成像平面等大小的虚拟图像平面(Virtual image plane),这样一来就不再是倒立的图像,而是直立图像。

有了相机后,上图中的蓝色盒子就变成了相机,上图中的物理成像平面Image plane也被数字化到由一个个pixel组成的sensor上,并保存下来。因此,对于相机而言,上图中的焦点就是相机的镜头,而上图中的物理成像平面,需要被转换成像素平面(pixel plane),物理成像平面(image plane)与像素平面(pixel plane)大小相同,计量单位不同。物理成像平面的单位是一个物理单位,例如mm,,而像素平面实际上就是一个二维图像,他的单位实际上是某某pixel在图像中的第几行第几列。
为了后续的描述方便我们这里先定义四个坐标系:
1,二维像平面(焦平面)坐标系Image plane,原点为,坐标轴用
,
表示。
2,二维图像坐标系pixel plane,原点为,坐标轴用
,
表示。
3,三维相机坐标系pinhole plane/camera,原点为,坐标轴用
,
,
表示。
4,三维世界坐标系world,原点为,坐标轴用
,
,
表示。
将3D世界场景映射成2D图像(像素平面pixel plane)总共分两步,第一步是把定义在世界坐标系中的实际3D物体映射到3D相机极坐标系中。相当于是把实际世界中的物体分别通过两个不同的坐标系来表示,然后通过找到这两个不同坐标系之间的差异,建立这两个坐标系之间的联系。这一转换关系就是下图中到
的转换。
从3D世界坐标系(world coordinates)到3D相机坐标系(camera coordinates),需要用到外参(extrinsic parameters)或外参矩阵(extrinsic matrix)--->[R t]。


其次,从3D相机坐标系(camera coordinates)到2D像素坐标系(pixel plane)需要用到内参(intrinsic parameters)或内参矩阵(intrinsic matrix)--->K。同样是把成像后的图像,用两个不同的坐标系来表示,然后再建立这两个坐标系(物理成像坐标系与二维图像坐标系)之间的联系,使两者可以相互转换。
extrinsic parameters外参:世界坐标系到相机坐标系
对于世界坐标系中的某一点大M而言,他本身是存在了,并不会因为我们有没有建立坐标系而受影响。但当我们人为的建立坐标系以后,这个点在我们所定义的坐标系下就有坐标值了。首先,对于点M而言,他在世界坐标系下可表示为M=[],而在相机坐标系中M=[
],这是同一个点,只不过在不同的坐标系所对应的坐标值不同。(其中:
中的上角标“M”表示点M,下角标"w"表示世界坐标系worl,以此类推,关于下角标的定义可参照我上面定义的四个坐标系。)
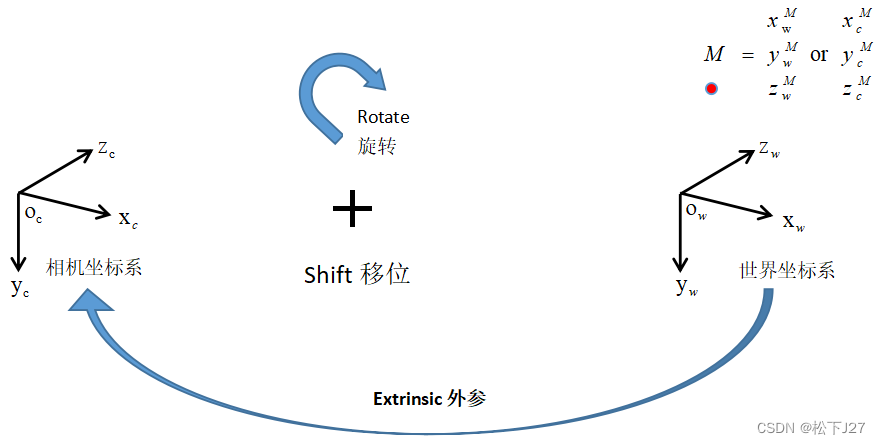
相机坐标系相对于世界坐标系而言,我们不能保证两个坐标系的原点完全重合,因此,对于x-y-z都存在一定的位移,由一个3x1矩阵t(translation)表示,其中每个元素分别对应了x-y-z方向上的位移:
此外,我们也不能保证相机在拍照时没有任何角度的偏差,因此,这两个坐标系的坐标轴存在一个整体的旋转。由一个3x3矩阵R(rotation)表示:
二者合并得到增广矩阵[R|t],使得:
其中:
这一数学表达式的意义是:一个在世界坐标系中定义的点,如果要用相机坐标系来表示,可以用矩阵[R|t]左乘该点的世界坐标系坐标实现。

这样一来就完成了大M点在世界坐标系下的坐标值到相机坐标系下的坐标值的转化:
Intrinsic parameters内参:
通过前面的研究,我们找到了世界坐标系与相机坐标系的联系,相当于学会了用相机坐标系来表示世界的物体(3D Object),现在,我们用相机坐标系来分别描述世界中的实际物体与“挪到前面来的”物理成像平面中物体的像,即,在相机坐标系中用不同的坐标值定义了世界中的实际物体大M点与虚拟成像平面上的像---小m点(图一),并找到他们之间的联系。

(图一)
表示光心,也叫摄影中心。过光心做垂直于物理成像平面的直线叫主光轴(principal axis),垂点
叫主点(principal point)。光心
与主点
之间的距离为焦距f。
现在,在相机坐标系中,我们令世界中的某一点大M的坐标值为M=[]。在虚拟成像平面中所成的像为小m,且小m的坐标值为m=[
](注意:x-y-z的上角标,我用大写的M表示实际点大M所对应的坐标值,用小写的m表示虚拟成像平面中的点小m)。同时,我们令主光轴与相机坐标系中的
轴重合,单看相机坐标系中由
与
轴组成的平面(图二),我们令大M在这一平面上的投影为
,令小m在
-
平面上的投影为
。
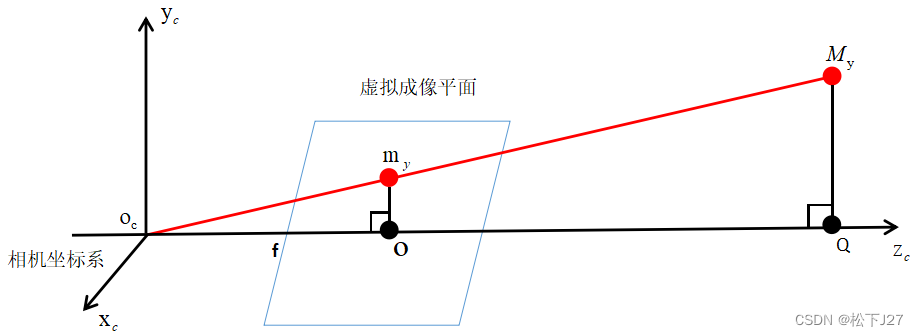
(图二)
在三角形中,线段
的长度为小m在
轴方向的坐标值
,线段
的长度为小m在
轴方向的坐标值
。在三角形
中,线段
的长度为
,线段
的长度为
。根据三角形
与三角形
相似,可以建立如下关系:
又因为小m点一定在物理成像平面上,则,在3D相机坐标系中,恒等于等于焦距f,代入上式后得出:
同样,如果单看相机坐标系中的与
轴所组成的平面(见图三),且用
表示大M在这一平面上的投影,用
表示小m在
-
平面上的投影:
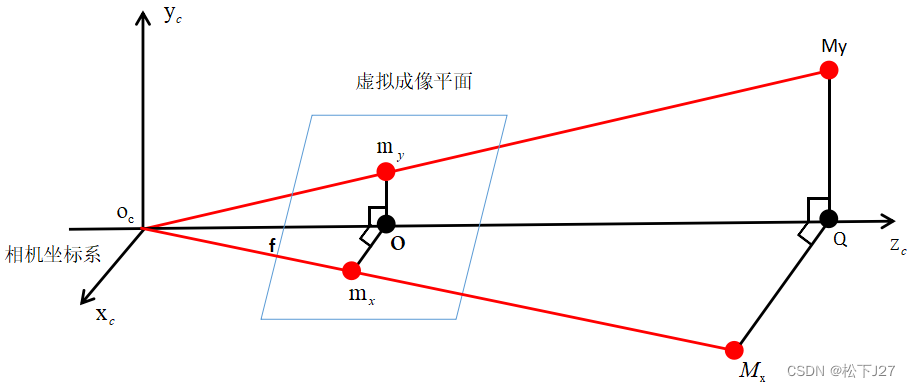
(图三)
根据相似相似三角形 与三角形
,可以建立如下关系
这样一来,我们就建立了世界中的大M与虚拟成像平面上的对应点小m,在相机坐标系中的关系:
(上面两式合称为公式1)
相机坐标系到像平面坐标系:
又因为,虚拟成像平面中的小m点,不仅在3D相机坐标系中,也在2D像平面坐标系中。且,像平面坐标系的中心在主光轴上。这就意味着,对于同一个点光心O而言,他在相机坐标系下的坐标值和在2D像平面坐标系下的坐标值相同。即,光心在相机坐标系下的坐标值为[=0,
=0],同时,他在2D像平面坐标系中的坐标值也等于[
=0,
=0]
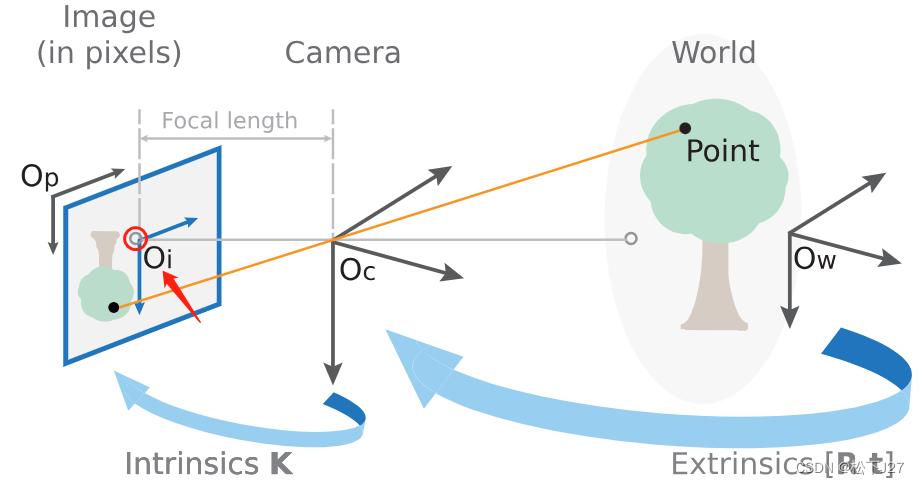
同理,已知相机坐标系中小m点的坐标值为m=[,
],令小m点在相平面中的坐标值为m=[
,
],则有:
(公式2)
如图四所示:

(图四)
这就完成了相机坐标系到像平面坐标系的转换。
像平面坐标系到图像坐标系:
在相机内部,物理成像平面被sensor以pixel为单位采样了,且,图像坐标系的原点在图像的左上角,见图五。因此,像平面坐标系中的小m点的坐标值,还需要一个转换关系。

(图五)
一方面,图像坐标系是用mxn个像素对像平面坐标系的采样。所以需要一个由mm为单位的像平面坐标系到以pixel为单位的图像坐标系的转换。
假设图像传感器的物理尺寸,也就是物理成像平面的大小为mxn(mm),传感器保存的图像尺寸为wxh(pixel)。要想把mxn的像保存到wxh的图上,则,以mm为单位的物理成像平面与以pixel为单位的图像之间的比例关系为:
第一个等式表示,图像中每个pixel的物理尺寸有多宽mm。
第二个等式表示,图像中每个pixel的物理尺寸有多高mm。
这样一来,就能用图像坐标系的坐标值(第几行第几列)来替换小m点在像平面坐标系中的坐标值(即,在方向的长度为
(mm)和在
方向的长度为
(mm)):
(公式3)
另一方面:二维图像坐标系的原点在图像(sensor)的左上角,而像平面坐标系的原点则是在senor的中心。因此,对于同一个点光心O而言,他在2D图像坐标系下的坐标值和在2D像平面坐标系下的坐标值不同,这两个坐标值之间存在一个偏移量Offset。我们在图像坐标系内定义方向上
到
的偏移量为
,他等于图像的宽度的一半---w/2,在
方向上
到
的偏移量为
,他等于图像的长度的一半---h/2。

光心O在图像坐标系中的坐标值是:
(公式4)
其中:
公式4的意思是:光心O在图像平面中的坐标值等于他在像平面中的坐标值加上一定的偏移量。同理,已经转换到图像坐标系内的小m点的坐标值(见公式3),加上Offset后为:
(公式5)
进一步,将公式2带入公式5后有:
然后再带入公式1,得到:
(公式6)
我们令,则上式可简化为:
(公式7)
其中:
1,表示以mm为单位的物理焦距f,在横向等于多少个像素。
2,表示以mm为单位的物理焦距f,在竖向等于多少个像素。
公式7用矩阵的方式可表示为:
其中的3x3矩阵,就叫内参矩阵,用大写的英文字母K表示。

总结:
最后我们来梳理一下整个转换过程:
1,大M点在世界坐标系下的坐标值[],通过外参矩阵[R t]得到了大M点在相机坐标系中的坐标值[
]。(通过同一点在不同坐标系中的坐标值,找到两个坐标系之间的关系。)
2,在相机坐标系中,根据相似三角形求出大M点在虚拟成像平面中所对应的小m点的坐标值[]。(通过同一坐标系下的不同点,找到这两个点之间坐标值的联系)
3,根据虚拟成像平面在相机坐标系中的位置,根据小m点在相机坐标系下的坐标值[,
,
]得到他在像平面坐标系下的坐标值[
=
,
=
]。(通过同一点在不同坐标系中的坐标值,找到两个坐标系之间的关系。)
4,最后,根据像平面坐标系与图像坐标系的相对关系,通过内参矩阵把小m点在像平面中的坐标值[,
]转到了图像坐标系中所对应的坐标值[
,
]。
参考文献:
1,https://www.cnblogs.com/xiaohuidi/p/15711767.html
2,What Is Camera Calibration?- MATLAB & Simulink- MathWorks 中国
3,2.3 透视投影的相机模型_哔哩哔哩_bilibili
版权声明:文中的部分图片,文字或者其他素材,可能来自很多不同的网站和说明,在此没法一一列出,如有侵权,请告知,立即删除。欢迎大家转载,但是,如果有人引用或者COPY我的文章,必须在你的文章中注明你所使用的图片或者文字来自于我的文章,否则,侵权必究。 ----松下J27
相关文章:
数字图像处理 --- 相机的内参与外参(CV学习笔记)
Pinhole Camera Model(针孔相机模型) 针孔相机是一种没有镜头、只有一个小光圈的简单相机。 光线穿过光圈并在相机的另一侧呈现倒立的图像。为了建模方便,我们可以把物理成像平面(image plane)上的图像移到实际场景(3D object)和焦点(focal p…...
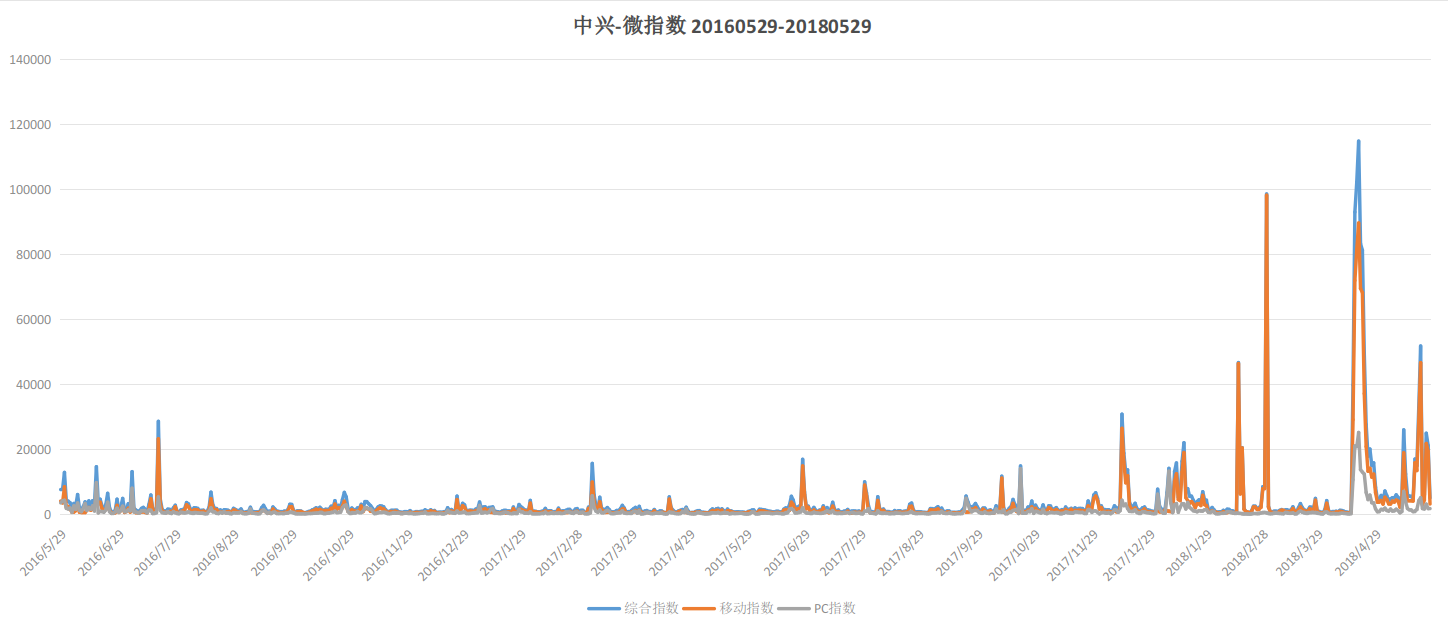
基于新浪微博海量用户行为数据、博文数据数据分析:包括综合指数、移动指数、PC指数三个指数
基于新浪微博海量用户行为数据、博文数据数据分析:包括综合指数、移动指数、PC指数三个指数 项目介绍 微指数是基于海量用户行为数据、博文数据,采用科学计算方法统计得出的反映不同事件领域发展状况的指数产品。微指数对于收录的关键词,在指…...
金融反欺诈的应用实践
“根据980起全球重大金融欺诈事件分析,60%的欺诈发生在移动端,同比增长170%。“,在香港近日举办的金融科技沙龙上,顶象金融业务安全专家史博表示,金融业已成为不法分子重要的攻击对象。 本届金融科技沙龙由Databricks…...
Win10启动Jmeter报错提示jmeter.log拒绝访问问题
jmeter版本:5.4.1 查看版本 在dos命令窗口中进入jmeter安装目录下的bin目录中:执行jmeter - v命令 我启动的方式是:进入jmeter安装目录下的bin目录中双击jmeter.bat启动的。结果报错,但是不影响使用。 报错日志如下: …...
Vue中使用Tailwind css
1.什么是Tailwind 就是一个CSS框架,和你知道的bootstrap,element ui,Antd,bulma。一样。将一些css样式封装好,用来加速我们开发的一个工具。 Tailwind解释 tailwind css 中文文档 2.Vue使用Tailwind配置 1. 新建vu…...

承接各种设计
小弟985研究生毕业,目前攻读读博士,可做各种设计,包括但不限于Matlab 电力电子/电气工程,matlab/simulink 电气专业仿真MATLAB 电气工程专业,matlab建模 电力电子,电气工程,电力系统,…...

HTTP请求性能分析 - 简单
使用随手可得的工具,尽量少的前置要求,来完成任务。 0. 目录 1. 前言2. 分析工具2.1 基于Chrome DevTools 的Timing2.1.1 关于Network标签页下的Timing部分2.1.2 一些注意项 2.2 基于Curl 命令 3. 剩下的工作 1. 前言 对于业务开发选手而言,…...

腾讯云标准型CVM云服务器详细介绍
腾讯云CVM服务器标准型实例的各项性能参数平衡,标准型云服务器适用于大多数常规业务,例如:web网站及中间件等,常见的标准型云服务器有CVM标准型S5、S6、SA3、SR1、S5se等规格,腾讯云服务器网来详细说下云服务器CVM标准…...

基于DEM tif影像的插值平滑和tif纹理贴图构建方法
准备数据是一个10米分辨率的Tif影像,直接用于生成DEM会十分的不平滑。如下图所示,平滑前后的对比效果图差异: 基于ArcGIS的DEM平滑插值 等值线生成(指定加密间距) 平滑线(指定平滑容差平滑等高线࿰…...

Redis_五种数据类型及操作命令
5.redis常用的五种数据类型 5.1 Redis String字符串 5.1.1 简介 String类型在redis中最常见的一种类型string类型是二制安全的,可以存放字符串、数值、json、图像数据value存储最大数据量是512M 5.1.2 常用命令 set < key>< value>:添加…...
Mac如何打开隐藏文件中Redis的配置文件redis.conf
Redis下载(通过⬇️博客下载的Redis默认路径为:/usr/local/etc) Redis下载 1.打开终端进入/usr文件夹 cd /usr 2.打开/local/文件夹 open local 3.找到redis.conf并打开,即可修改配置信息...
nginx+flask+uwsgi部署遇到的坑
文章目录 1.环境:2.uwsgi_conf.ini具体配置内容3.nginx 具体配置4.具体命令(注意使用pip3命令安装)5.服务异常排查 1.环境: centos8 uWSGI 2.0.22 gmssl 3.2.2 nginx version: nginx/1.18.0 项目目录: 2.uwsgi_conf.ini具体配置内容 [uws…...

vue实现pdf预览功能
背景:材料上传之后点击预览实现在浏览器上预览的效果 效果如下: 实现代码如下: //预览和下载操作 <el-table-column fixed"right" label"操作" width"210"><template #default"scope">…...

(原创)Flutter与Native页面互相跳转
前言 实际开发混合项目时,常常会有页面跳转的需求 如果是原生界面和flutter界面需要互相跳转 这种情况应该怎么处理呢? 今天这篇博客主要就来介绍下这个情况 其实想一下,这个问题可以拆成四个小的问题来分析: 1:原生界…...

web集群学习--基于CentOS构建LVS-DR集群、配置nginx负载均衡
基于CentOS构建LVS-DR集群 环境准备 主机名 ip地址 node1 192.168.1.140 client node2 192.168.1.141 LVS node3 192.168.1.142 RS1 node4 192.168.1.143 RS2配置 1.关闭防火墙和SELinux [rootclient~]# systemctl stop firewalld [rootclient~]# systemctl disabl…...

基于 FPGA 的电机控制
FPGA 非常适合精密电机控制,在这个项目中,我们将创建一个简单的电机控制程序,在此基础上可以构建更复杂的应用。 需要的硬件 Digilent Pmod HB3 介绍 我们可以用一个简单的 8 位微控制器来控制电机,输出一个简单的脉宽调制波形。然…...
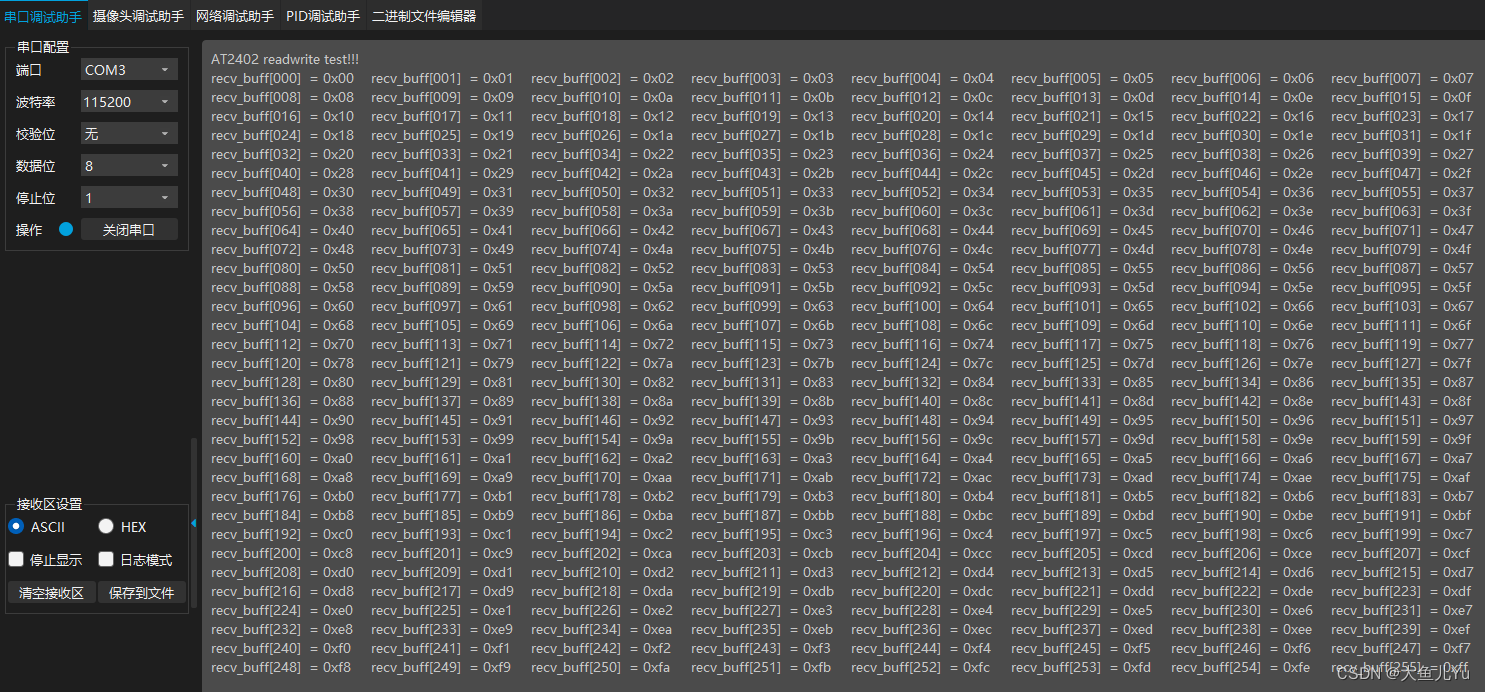
STM32F429IGT6使用CubeMX配置IIC通信(AT2402芯片)
1、硬件电路 写地址:0xA0 读地址:0xA1 存储容量:256Byte 2、设置RCC,选择高速外部时钟HSE,时钟设置为180MHz 3、配置IIC 4、生成工程配置 5、部分代码 #define IIC_WRITE_ADDR 0xA0 // IIC写地址 #define IIC_READ_ADDR 0xA1 …...
JS逆向系列之猿人学爬虫第14题-备而后动-勿使有变
文章目录 题目地址参数分析参考jspython 调用往期逆向文章推荐题目地址 https://match.yuanrenxue.cn/match/14题目难度标的是困难,主要难在js混淆部分。 参数分析 初始抓包有无限debugger反调试,可以直接hook 函数构造器过掉无限debugger Function.prototype.__construc…...

学cpp看的那点书
C C Primer 语言基础学习 C Templates The Complete Guide (2nd Edition) 学习模板,更好的阅读 STL 源码,毕竟C 标准库大部分是模板。 The C Standard Library 全称 The C Standard Library A Tutorial and Reference Second Edition简单的了解标…...
【C++】常用容器-string容器
1.string基本概念 2.string构造函数 #include <iostream> using namespace std;//string容器 void test01() {string s1;//创建空字符串,调用无参构造函数cout << "str1 " << s1 << endl;//什么都不输出const char* str "…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...
