当前位置： 首页 > news >正文

React入门学习笔记3

news 2026/2/10 21:27:52

事件处理

  1. 通过onXxx属性指定事件处理函数(注意大小写)
    1. React使用的是自定义(合成)事件, 而不是使用的原生DOM事件——为了更好的兼容性 eg：οnclick==》onClick
    2. React中的事件是通过事件委托方式处理的(委托给组件最外层的元素)——为了更高效
  2. 通过event.target得到发生事件的DOM元素对象——所以不要过度使用ref
  3. 当事件项和操作项是同一个时无需使用ref

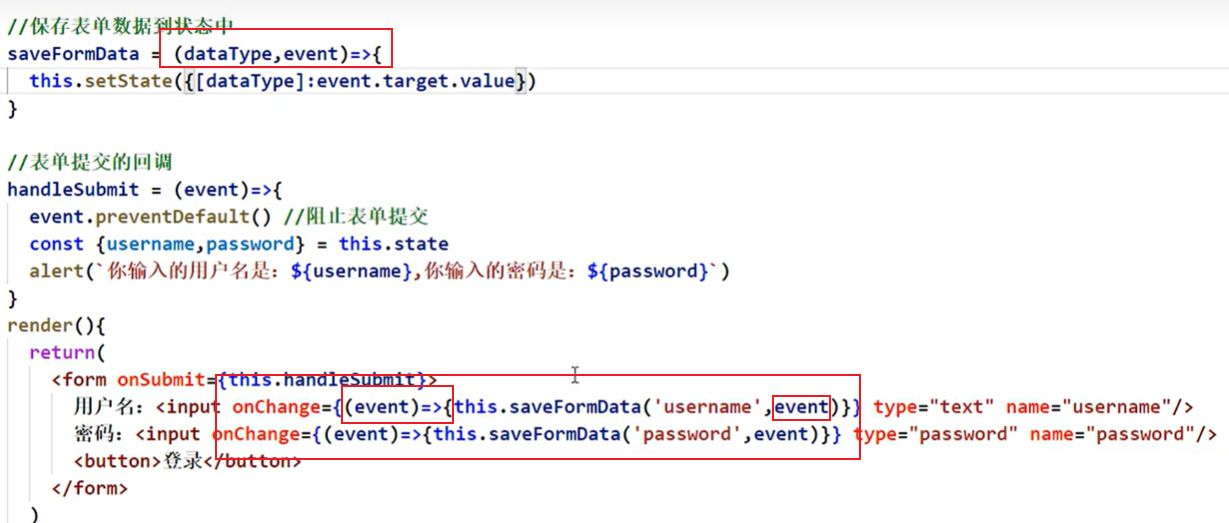
 非受控组件

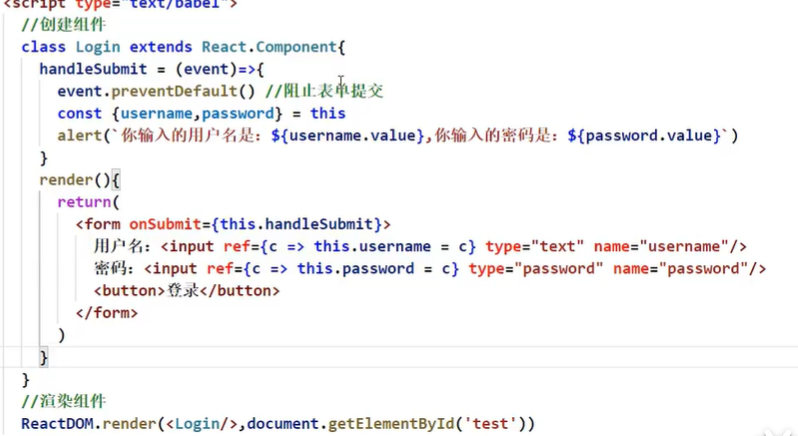
数据现用现取

调用event.preventDefault()阻止表单提交 

受控组件

优势就是双向绑定，能省掉ref

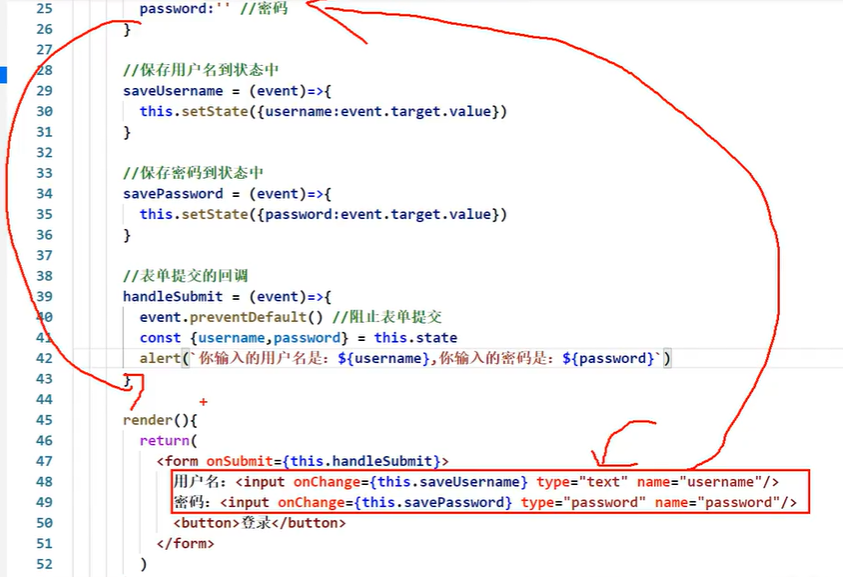
很明显，这样子实在是太麻烦了。。所以就有了⬇

高阶函数——函数柯里化

如果一个函数符合下面2个规范中的任何一个，那该函数就是高阶函数。
        1.若A函数，接收的参数是一个函数，那么A就可以称之为高阶函数。
        2.若A函教，调用的返回值依然是一个函数，那么A就可以称之为高阶函数。

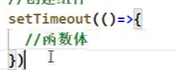
常见的高阶函数有：Promise、setTimeout、arr.map()等等

 

函数的柯里化: 通过函数调用继续返回函数的方式，实现多次接收参数最后统一处理的函数编码形式。

重点就是分步接受参数并在最后统一处理！！

这里运用了闭包

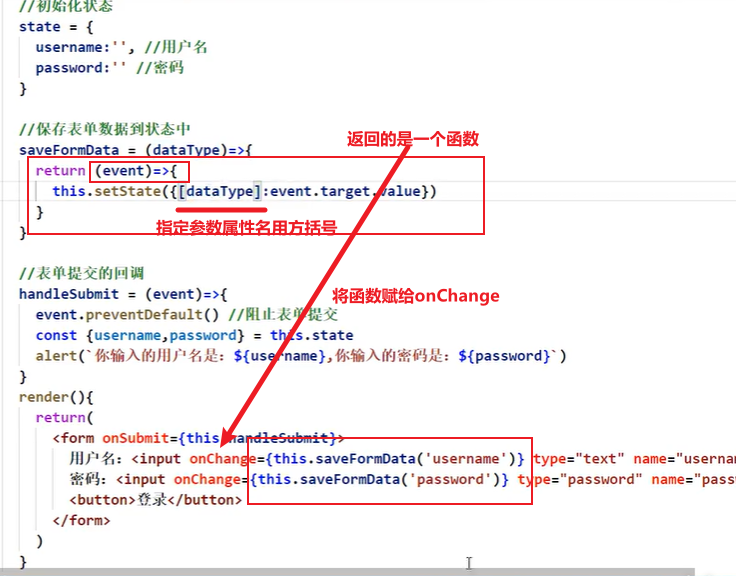
 指定参数属性名用方括号！！！

细品上面的例子，非常巧妙。

但其实，也可以一次性获取参数和event，只需要在调用时写个内联函数

 

相关文章：

React入门学习笔记3

事件处理 通过onXxx属性指定事件处理函数(注意大小写) React使用的是自定义(合成)事件, 而不是使用的原生DOM事件——为了更好的兼容性 eg：οnclick》onClickReact中的事件是通过事件委托方式处理的(委托给组件最外层的元素)——为了更高效通过event.target得到发生…...

编程日记 2023/8/13 11:40:03

从零开始理解Linux中断架构（25)中断运行全景实例

前面我们基本理解了软中断处理的基本框架，为了对中断调用有一个全景的直观感受，我们在网卡驱动程序的中断函数dump_stack,观看一下各种情况下的软中断调用call Stack的情况。 （1）ksoftirqd处理软中断的情况 有线以太网卡NAPI轮询的调用栈 [ 106.374117] Hardware name: K…...

编程日记 2023/8/13 11:39:02

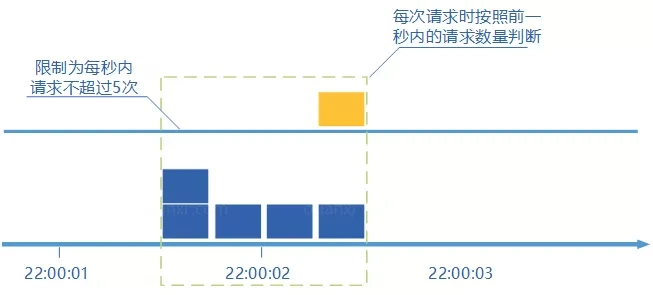
go-zero 是如何实现计数器限流的？

原文链接： 如何实现计数器限流？ 上一篇文章 go-zero 是如何做路由管理的？ 介绍了路由管理，这篇文章来说说限流，主要介绍计数器限流算法，具体的代码实现，我们还是来分析微服务框架 go-zero 的源…...

编程日记 2023/8/13 11:38:00

【考研复习】24王道数据结构课后习题代码｜第3章栈与队列

文章目录 3.1 栈3.2 队列3.3 栈和队列的应用 3.1 栈 int symmetry(linklist L,int n){char s[n/2];lnode *pL->next;int i;for(i0;i<n/2;i){s[i]p->data;pp->next;}i--;if(n%21) pp->next;while(p&&s[i]p->data){i--;pp->next;}if(i-1) return 1;…...

编程日记 2023/8/13 11:37:00

java中excel文件下载

1、System.getProperty(user.dir) 获取的是启动项目的容器位置 2、 Files.copy(sourceFile.toPath(), destinationFile.toPath(), StandardCopyOption.REPLACE_EXISTING); StandardCopyOption.REPLACE_EXISTING 来忽略文件已经存在的异常&#xff0c;如果存在就去覆盖掉它Sta…...

编程日记 2023/8/13 11:35:59

29 | 广州美食店铺数据分析

广州美食店铺数据分析 一、数据分析项目MVP加/价值主张宣言 随着经济的快速发展以及新媒体的兴起，美食攻略、美食探店等一系列东西进入大众的眼球，而人们也会在各大平台中查找美食推荐，因此本项目做的美食店铺数据分析也是带有可行性的。首先通过对广东省的各市美食店铺数量…...

编程日记 2023/8/13 11:34:58

fastApi基础

1、fastApi简介 官方文档&#xff1a;https://fastapi.tiangolo.com/ 源码&#xff1a; https://github.com/tiangolo/fastapi 2、环境准备 安装python 安装pycharm 安装fastAPI 安装 uvicorn 查看已经安装的第三方库&#xff1a;pip list 查看pip 配置信息&#xff1a;pip co…...

编程日记 2023/8/13 11:33:55

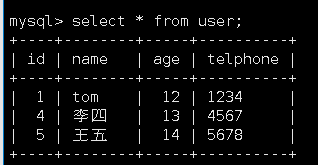
Mysql整理二 - 常见查询语句面试题(附原表)

表结构&#xff0c;创建原表的代码在最后 -- cid课程id; tid老师id; sid学生id; select * from t_mysql_course; select * from t_mysql_score; select * from t_mysql_student; select * from t_mysql_teacher; 1. 查询" 01 “课程比” 02 "课程成绩高的学生的信息…...

编程日记 2023/8/13 11:32:53

Python - 读取pdf、word、excel、ppt、csv、txt文件提取所有文本

前言 本文对使用python读取pdf、word、excel、ppt、csv、txt等常用文件&#xff0c;并提取所有文本的方法进行分享和使用总结。 可以读取不同文件的库和方法当然不止下面分享的这些&#xff0c;本文的代码主要目标都是&#xff1a;方便提取文件中所有文本的实现方式。 这些库的…...

编程日记 2023/8/13 11:31:53

Codeforces Round 892 (Div. 2) C. Another Permutation Problem 纯数学方法 思维题

Codeforces Round 892 (Div. 2) C. Another Permutation Problem 源码&#xff1a; #include <iostream> #include <algorithm> #include <set> #include <map> #include <queue> #include <vector> #include <stack> #include &l…...

编程日记 2023/8/13 11:30:51

持续输出：自媒体持续输出文字内容、视音频创作（视频课程、书籍章节）

以下是自媒体持续输出文字内容、视音频创作的最佳方法&#xff1a; 灵感来源&#xff1a;寻找灵感来源是自媒体创作的重要一环。可以从日常生活、网络热点、行业动态等方面寻找创作灵感。 确定主题&#xff1a;在确定主题的时候&#xff0c;需要根据读者和观众的需求&#xff…...

编程日记 2023/8/13 11:29:47

篇十七：备忘录模式：恢复对象状态

篇十七&#xff1a;"备忘录模式&#xff1a;恢复对象状态" 开始本篇文章之前先推荐一个好用的学习工具&#xff0c;AIRIght&#xff0c;借助于AI助手工具&#xff0c;学习事半功倍。欢迎访问&#xff1a;http://airight.fun/。 另外有2本不错的关于设计模式的资料&…...

编程日记 2023/8/13 11:28:46

初识mysql数据库之图形化界面

目录 一、好用的数据库图形化界面软件 1. Navicat 2. SQLyog 3. MYSQL Workbench 二、MYSQL Workbench基本使用 1. 安装 2. 远端连接 3. 执行sql语句 一、好用的数据库图形化界面软件 在以前的文章中&#xff0c;一共介绍了两种使用数据库的方式&#xff0c;分别为在l…...

编程日记 2023/8/13 11:27:45

APP外包开发的H5开发框架

跨平台移动应用开发框架允许开发者使用一套代码在多个操作系统上构建应用程序&#xff0c;从而节省时间和资源。以下是一些常见的跨平台移动应用开发框架以及它们的特点&#xff0c;希望对大家有所帮助。北京木奇移动技术有限公司&#xff0c;专业的软件外包开发公司&#xff0…...

编程日记 2023/8/13 11:26:44

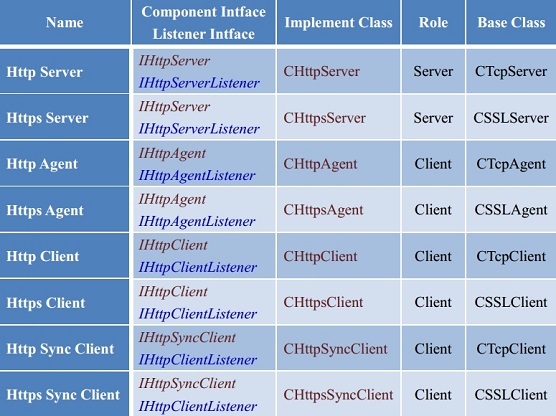
高性能跨平台网络通信框架 HP-Socket v5.9.3

项目主页 : http://www.oschina.net/p/hp-socket开发文档 : https://www.docin.com/p-4478351216.html下载地址 : https://github.com/ldcsaa/HP-SocketQQ Group: 44636872, 663903943 v5.9.3 更新 一、主要更新 问题修复&#xff1a;通过 POST/PUT 等带有请求内容的 HTTP 方…...

编程日记 2023/8/13 11:25:43

Vue3.2+TS在v-for的时候，循环处理时间，将其变成xx-xx-xx xx:xx:xx格式，最后教给大家自己封装一个时间hooks，直接复用

Vue3.2TS在v-for的时候&#xff0c;循环处理时间&#xff0c;将其变成xx-xx-xx xx:xx:xx格式 最后教给大家自己封装一个时间hooks&#xff0c;直接复用 1.没有封装&#xff0c;直接使用 <template><div><ul><li v-for"item,index in arr" :k…...

编程日记 2023/8/13 11:24:41

05 mysql innodb page

前言 最近看到了 何登成 大佬的 "深入MySQL源码 -- Step By Step" 的 pdf 呵呵 似乎是找到了一些 方向 之前对于 mysql 方面的东西, 更多的仅仅是简单的使用[业务中的各种增删改查], 以及一些面试题的背诵 这里会参照 MySQL Internals Manual 来大致的看一下 i…...

编程日记 2023/8/13 11:23:39

记录一次electron打包提示文件找不到的解决方法

没有配置files选项 files的作用是配置打包到应用程序的构建资源 就是说如果你想使用项目那个目录下的文件 就得通过files配置一下不然就会报错 json文件或者yml文件会报的错 格式是这样的 "files": ["dist-electron", "dist"],electron打包配…...

编程日记 2023/8/13 11:22:38

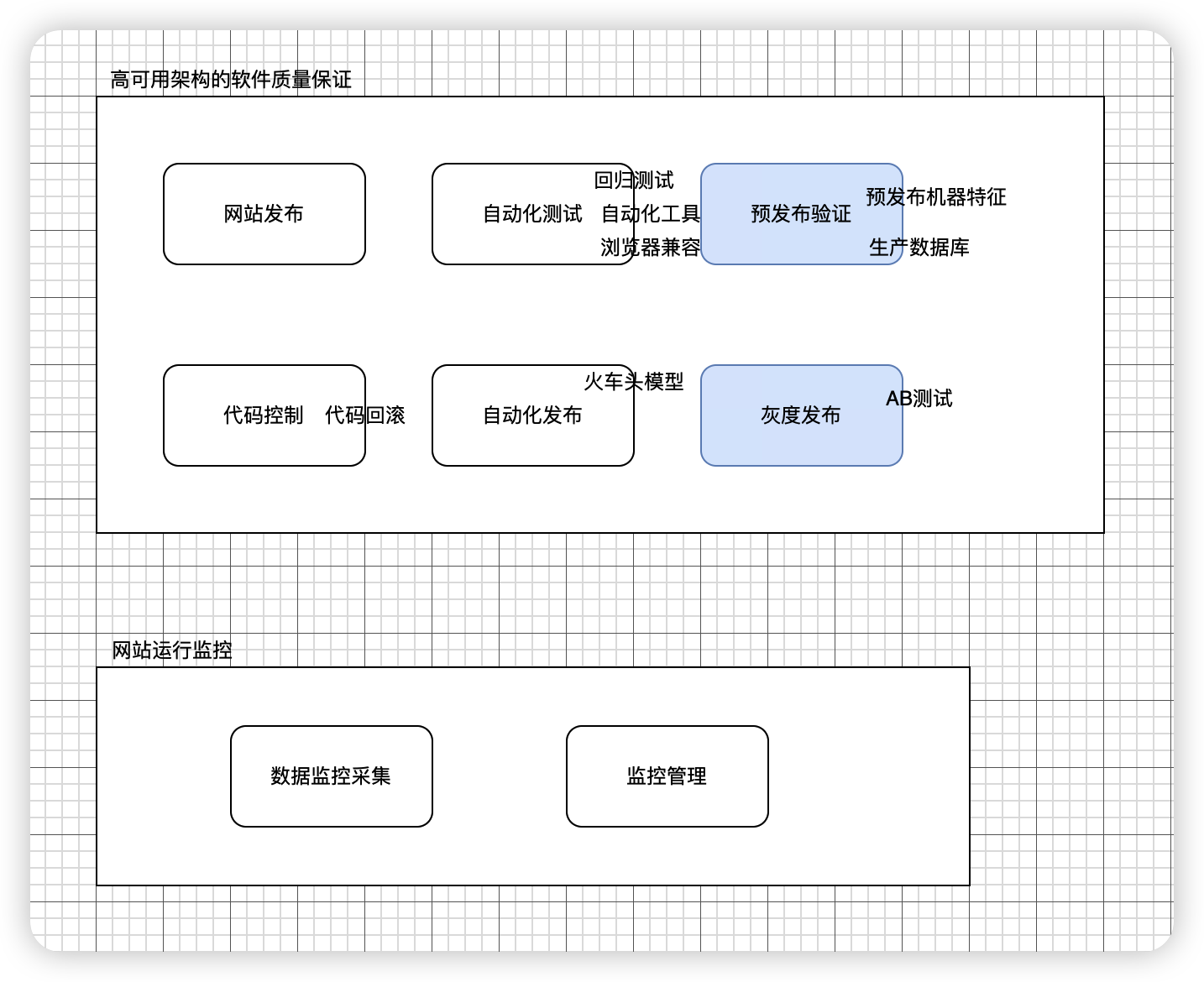
《大型网站技术架构》第二篇 架构-高可用

高可用在公司中的重要性 对公司而言&#xff0c;可用性关系网站的生死存亡。对个人而言&#xff0c;可用性关系到自己的绩效升迁。 工程师对架构做了许多优化、对代码做了很多重构&#xff0c;对性能、扩展性、伸缩性做了很多改善&#xff0c;但别人未必能直观地感受到&#…...

编程日记 2023/8/13 11:21:36

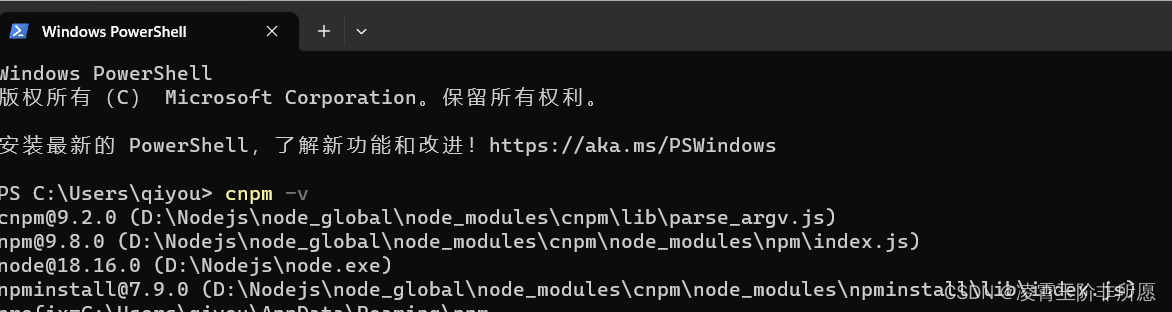
VS Code 使用cnpm下载包失败

一、 问题如下&#xff1a; 网上找到的解决方法是要在powershell中执行&#xff1a; Set-ExecutionPolicy RemoteSigned进行更改策略。 首先我们解释下这个Set-ExecutionPolicy RemoteSigned&#xff0c;Set-ExecutionPolicy 是一个 PowerShell 命令&#xff0c;用于控制脚本…...

编程日记 2023/8/13 11:20:34

装饰模式（Decorator Pattern）重构java邮件发奖系统实战

前言 现在我们有个如下的需求&#xff0c;设计一个邮件发奖的小系统&#xff0c; 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式&#xff08;Decorator Pattern&#xff09;允许向一个现有的对象添加新的功能&#xff0c;同时又不改变其…...

编程新知 2026/2/8 4:37:00

地震勘探——干扰波识别、井中地震时距曲线特点

目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波&#xff1a;可以用来解决所提出的地质任务的波&#xff1b;干扰波&#xff1a;所有妨碍辨认、追踪有效波的其他波。 地震勘探中&#xff0c;有效波和干扰波是相对的。例如&#xff0c;在反射波…...

编程新知 2026/2/8 20:43:05

【OSG学习笔记】Day 18: 碰撞检测与物理交互

物理引擎&#xff08;Physics Engine&#xff09; 物理引擎 是一种通过计算机模拟物理规律&#xff08;如力学、碰撞、重力、流体动力学等&#xff09;的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互&#xff0c;广泛应用于 游戏开发、动画制作、虚…...

编程新知 2026/2/4 2:08:30

模型参数、模型存储精度、参数与显存

模型参数量衡量单位 M&#xff1a;百万&#xff08;Million&#xff09; B&#xff1a;十亿&#xff08;Billion&#xff09; 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的&#xff0c;但是一个参数所表示多少字节不一定&#xff0c;需要看这个参数以什么…...

编程新知 2025/12/20 12:32:08

MongoDB学习和应用(高效的非关系型数据库)

一丶 MongoDB简介 对于社交类软件的功能&#xff0c;我们需要对它的功能特点进行分析&#xff1a; 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具&#xff1a; mysql&#xff1a;关系型数据库&am…...

编程新知 2026/1/23 10:24:30

渗透实战PortSwigger靶场-XSS Lab 14：大多数标签和属性被阻止

<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet&#xff1a; https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

编程新知 2026/1/24 13:05:24

YSYX学习记录（八）

C语言&#xff0c;练习0&#xff1a; 先创建一个文件夹&#xff0c;我用的是物理机&#xff1a; 安装build-essential 练习1&#xff1a; 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件&#xff0c;随机修改或删除一部分&#xff0c;之后…...

编程新知 2026/1/24 14:31:01

前端开发面试题总结-JavaScript篇(一)

文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包&#xff08;Closure&#xff09;&#xff1f;闭包有什么应用场景和潜在问题&#xff1f;2.解释 JavaScript 的作用域链&#xff08;Scope Chain&#xff09; 二、原型与继承3.原型链是什么&#xff1f;如何实现继承&a…...

编程新知 2026/2/1 3:12:03

ios苹果系统，js 滑动屏幕、锚定无效

现象&#xff1a;window.addEventListener监听touch无效&#xff0c;划不动屏幕&#xff0c;但是代码逻辑都有执行到。 scrollIntoView也无效。 原因&#xff1a;这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作&#xff0c;从而会影响…...

编程新知 2026/2/4 19:47:03

AspectJ 在 Android 中的完整使用指南

一、环境配置&#xff08;Gradle 7.0 适配&#xff09; 1. 项目级 build.gradle // 注意&#xff1a;沪江插件已停更&#xff0c;推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

编程新知 2025/7/7 22:33:57