当前位置： 首页 > news >正文

高性能跨平台网络通信框架 HP-Socket v5.9.3

news 2026/2/10 23:53:07

HP-Socket

  • 项目主页 : http://www.oschina.net/p/hp-socket
  • 开发文档 : https://www.docin.com/p-4478351216.html
  • 下载地址 : https://github.com/ldcsaa/HP-Socket
  • QQ Group: 44636872, 663903943

v5.9.3 更新

一、主要更新
  1. 问题修复：通过 POST/PUT 等带有请求内容的 HTTP 方法升级 websocket 协议时，可能会导致 HTTP Server 异常
  2. UDP Client/Server 之间的单个心跳包发送失败不会立刻断开连接，只检测心跳是否超时来判断是否要断开连接
二、第三方库更新
  1. openssl 升级到 1.1.1v 版本
  2. llhttp 升级到 8.1.1 版本

HP-Socket 组件列表

  • 基础组件
    基础组件
  • SSL 组件
    SSL 组件
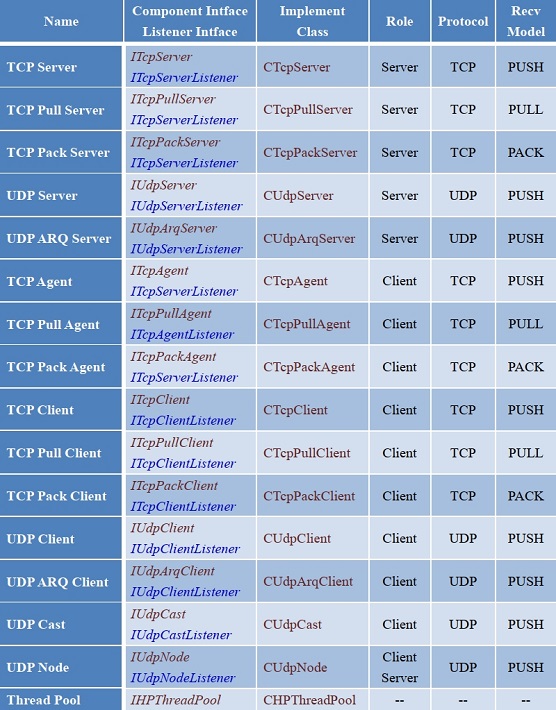
  • HTTP 组件
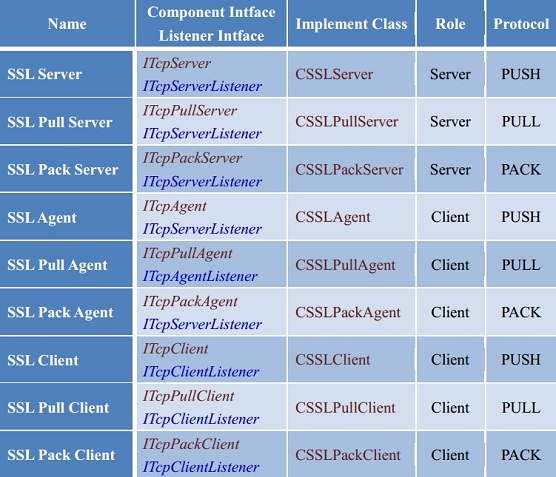
    HTTP 组件

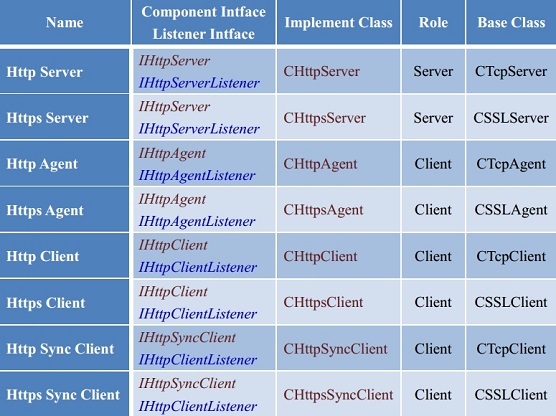
相关文章：

高性能跨平台网络通信框架 HP-Socket v5.9.3

项目主页 : http://www.oschina.net/p/hp-socket开发文档 : https://www.docin.com/p-4478351216.html下载地址 : https://github.com/ldcsaa/HP-SocketQQ Group: 44636872, 663903943 v5.9.3 更新 一、主要更新 问题修复：通过 POST/PUT 等带有请求内容的 HTTP 方…...

编程日记 2023/8/13 11:25:43

Vue3.2+TS在v-for的时候，循环处理时间，将其变成xx-xx-xx xx:xx:xx格式，最后教给大家自己封装一个时间hooks，直接复用

Vue3.2TS在v-for的时候&#xff0c;循环处理时间&#xff0c;将其变成xx-xx-xx xx:xx:xx格式 最后教给大家自己封装一个时间hooks&#xff0c;直接复用 1.没有封装&#xff0c;直接使用 <template><div><ul><li v-for"item,index in arr" :k…...

编程日记 2023/8/13 11:24:41

05 mysql innodb page

前言 最近看到了 何登成 大佬的 "深入MySQL源码 -- Step By Step" 的 pdf 呵呵 似乎是找到了一些 方向 之前对于 mysql 方面的东西, 更多的仅仅是简单的使用[业务中的各种增删改查], 以及一些面试题的背诵 这里会参照 MySQL Internals Manual 来大致的看一下 i…...

编程日记 2023/8/13 11:23:39

记录一次electron打包提示文件找不到的解决方法

没有配置files选项 files的作用是配置打包到应用程序的构建资源 就是说如果你想使用项目那个目录下的文件 就得通过files配置一下不然就会报错 json文件或者yml文件会报的错 格式是这样的 "files": ["dist-electron", "dist"],electron打包配…...

编程日记 2023/8/13 11:22:38

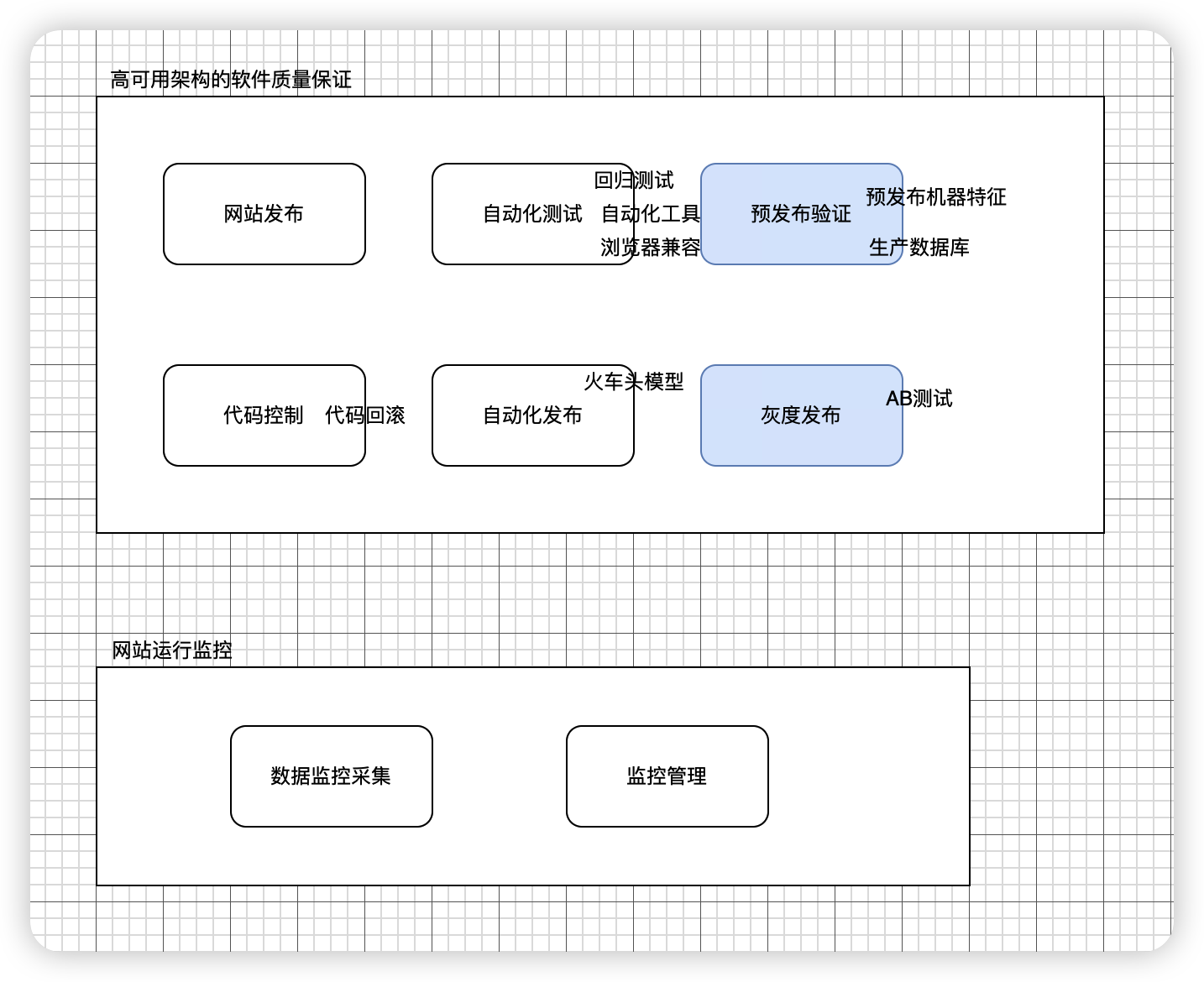
《大型网站技术架构》第二篇 架构-高可用

高可用在公司中的重要性 对公司而言&#xff0c;可用性关系网站的生死存亡。对个人而言&#xff0c;可用性关系到自己的绩效升迁。 工程师对架构做了许多优化、对代码做了很多重构&#xff0c;对性能、扩展性、伸缩性做了很多改善&#xff0c;但别人未必能直观地感受到&#…...

编程日记 2023/8/13 11:21:36

VS Code 使用cnpm下载包失败

一、 问题如下&#xff1a; 网上找到的解决方法是要在powershell中执行&#xff1a; Set-ExecutionPolicy RemoteSigned进行更改策略。 首先我们解释下这个Set-ExecutionPolicy RemoteSigned&#xff0c;Set-ExecutionPolicy 是一个 PowerShell 命令&#xff0c;用于控制脚本…...

编程日记 2023/8/13 11:20:34

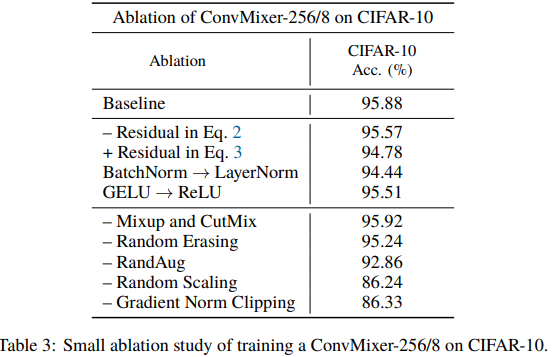
【图像分类】CNN + Transformer 结合系列.4

介绍两篇利用Transformer做图像分类的论文&#xff1a;CoAtNet&#xff08;NeurIPS2021&#xff09;&#xff0c;ConvMixer&#xff08;ICLR2022&#xff09;。CoAtNet结合CNN和Transformer的优点进行改进&#xff0c;ConvMixer则patch的角度来说明划分patch有助于分类。 CoAtN…...

编程日记 2023/8/13 11:19:32

分享一下利用Vue表单处理实现复杂表单布局

在开发Web应用程序中&#xff0c;表单是非常常见的一种元素。而在某些情况下&#xff0c;我们需要实现一些更为复杂的表单布局&#xff0c;以满足业务需求。使用Vue.js作为前端框架&#xff0c;我们可以很方便地处理复杂表单布局&#xff0c;并且实现数据的双向绑定。 下面来将…...

编程日记 2023/8/13 11:18:30

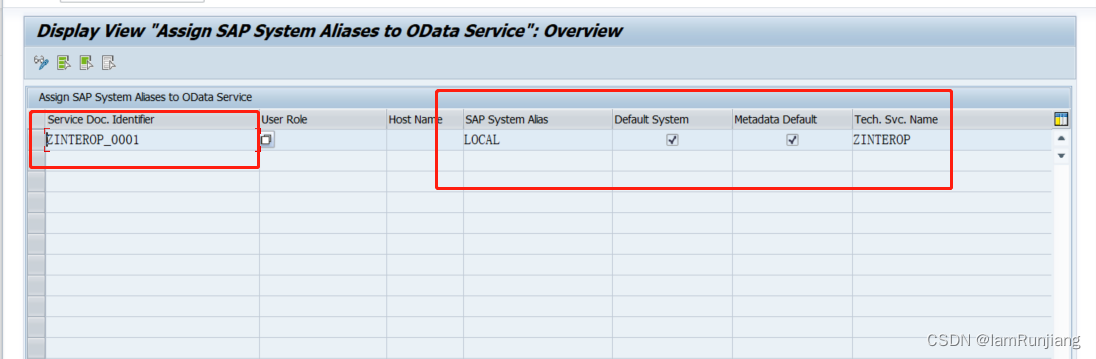
SAP Fiori 问题收集

事务代码篇 启动工作台&#xff1a;/N/UI2/FLP 错误日志&#xff1a; /n/IWFND/ERROR_LOG 服务清单&#xff1a; /n/IWFND/MAINT_SERVICE 创建语义对象&#xff1a;/N/UI2/SEMOBJ 创建目录&#xff1a;/N/UI2/FLPD_CONF&#xff08;cross-client&#xff09;或 /N/UI2…...

编程日记 2023/8/13 11:17:29

econml双机器学习实现连续干预和预测

连续干预 在这个示例中&#xff0c;我们使用LinearDML模型&#xff0c;使用随机森林回归模型来估计因果效应。我们首先模拟数据&#xff0c;然后模型&#xff0c;并使用方法来effect创建不同干预值下的效应&#xff08;Conditional Average Treatment Effect&#xff0c;CATE&…...

编程日记 2023/8/13 11:16:26

《甲午》观后感——GPT-3.5所写

《甲午》是一部令人深思的纪录片&#xff0c;通过生动的画面和真实的故事&#xff0c;向观众展示了中国历史上的一段重要时期。观看这部纪录片&#xff0c;我深受触动&#xff0c;对历史的认识也得到了深化。 首先&#xff0c;这部纪录片通过精心搜集的历史资料和珍贵的影像资料…...

编程日记 2023/8/13 11:15:24

Java技术整理（6）—— 微服务篇

1、服务注册发现 服务注册就是维护一个服务列表&#xff0c;它在管理系统内所有的服务地址&#xff0c;当新的服务启动后&#xff0c;它会向服务列表提交自己的服务地址&#xff0c;服务的调用法可以直接向服务列表发送服务列表获取请求&#xff0c;就能获得所有的服务地址&am…...

编程日记 2023/8/13 11:14:21

途乐证券-新股行情持续火爆，哪些因素影响首日表现？

全面注册制以来&#xff0c;参加打新的投资者数量全体呈现下降。打新收益下降&#xff0c;破发频出的布景下&#xff0c;投资者打新策略从逢新必打逐步向优选个股改变。 经过很多历史数据&#xff0c;从商场定价、参加者热度以及机构重视度维度揭秘了上市后股价体现优秀的个股具…...

编程日记 2023/8/13 11:13:19

在生产环境中部署Elasticsearch：最佳实践和故障排除技巧——聚合与搜索（三）

前言 「作者主页」&#xff1a;雪碧有白泡泡 「个人网站」&#xff1a;雪碧的个人网站 「推荐专栏」&#xff1a; ★java一站式服务 ★ ★ React从入门到精通★ ★前端炫酷代码分享 ★ ★ 从0到英雄&#xff0c;vue成神之路★ ★ uniapp-从构建到提升★ ★ 从0到英雄&#xff…...

编程日记 2023/8/13 11:12:16

基于weka手工实现KNN

一、KNN模型 K最近邻&#xff08;K-Nearest Neighbors&#xff0c;简称KNN&#xff09;算法是一种常用的基于实例的监督学习算法。它可以用于分类和回归问题&#xff0c;并且是一种非常直观和简单的机器学习算法。 KNN算法的基本思想是&#xff1a;对于一个新的样本数据&…...

编程日记 2023/8/13 11:11:15

Lua 闭包

一、Lua 中的函数 Lua 中的函数是第一类值。意味着和其他的常见类型的值&#xff08;例如数值和字符串&#xff09;具有同等权限。 举个例子&#xff0c;函数也可以像其他类型一样存储起来&#xff0c;然后调用 -- 将 a.p 指向 print 函数 a { p print } -- 使用 a.p 函数…...

编程日记 2023/8/13 11:10:14

Java技术整理（1）—— JVM篇

1、什么是JVM&#xff1f; JVM是一个可运行Java代码的虚拟计算机&#xff0c;包括一套字节码指令集&#xff0c;一组寄存器&#xff0c;一个栈&#xff0c;一个垃圾回收&#xff0c;堆和一个存储方式栈。JVM 是运行在操作系统之上&#xff0c;并不与操作系统直接交互。 2、运行…...

编程日记 2023/8/13 11:09:12

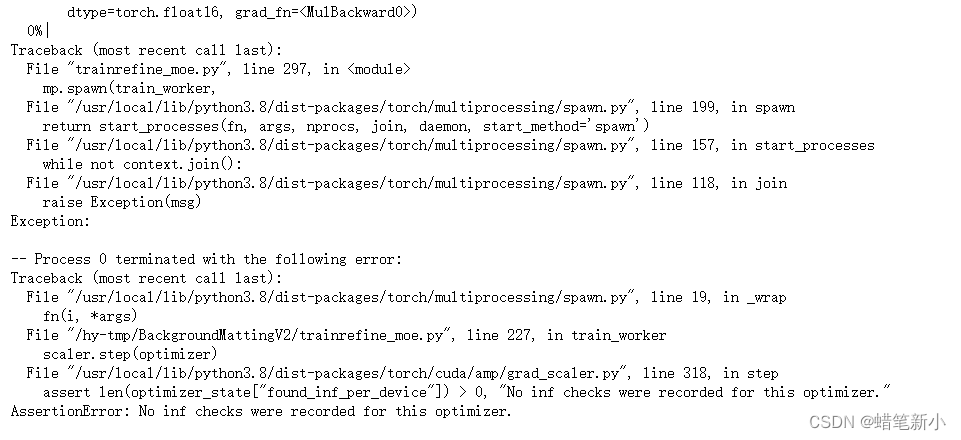
bug解决：AssertionError: No inf checks were recorded for this optimizer.

这真的是最恶心的一个error&#xff08;比网络回传找哪层没有传播到还要恶心&#xff01;&#xff09;&#xff0c;找了好久的问题所在之处&#xff0c;最后偶然发现了这篇文章&#xff1a; 解决pytorch半精度amp训练nan问题 - 知乎 然后发现自己用的混合精度训练&#xff0c;发…...

编程日记 2023/8/13 11:08:11

Django笔记之数据库查询优化汇总

1、性能方面 1. connection.queries 前面我们介绍过 connection.queries 的用法&#xff0c;比如我们执行了一条查询之后&#xff0c;可以通过下面的方式查到我们刚刚的语句和耗时 >>> from django.db import connection >>> connection.queries [{sql: S…...

编程日记 2023/8/13 11:07:09

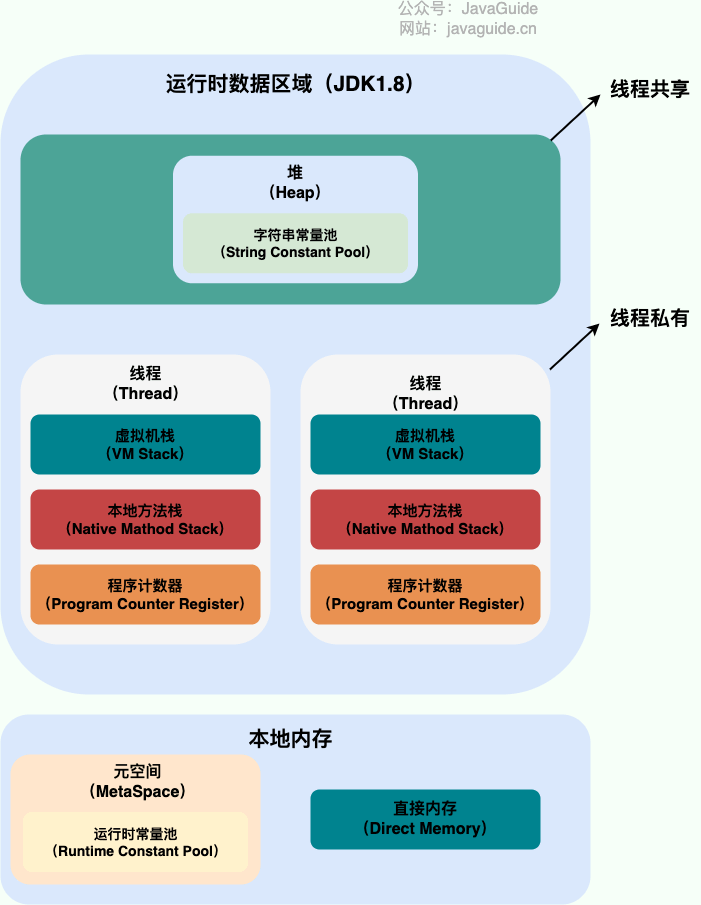
JVM内存区域

预备 为了更好的理解类加载和垃圾回收&#xff0c;先要了解一下JVM的内存区域&#xff08;如果没有特殊说明&#xff0c;都是针对的是 HotSpot 虚拟机。&#xff09;。 Java 源代码文件经过编译器编译后生成字节码文件&#xff0c;然后交给 JVM 的类加载器&#xff0c;加载完…...

编程日记 2023/8/13 11:06:08

【OSG学习笔记】Day 18: 碰撞检测与物理交互

物理引擎&#xff08;Physics Engine&#xff09; 物理引擎 是一种通过计算机模拟物理规律&#xff08;如力学、碰撞、重力、流体动力学等&#xff09;的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互&#xff0c;广泛应用于 游戏开发、动画制作、虚…...

编程新知 2026/2/4 2:08:30

Day131 | 灵神 | 回溯算法 | 子集型 子集

Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣&#xff08;LeetCode&#xff09; 思路&#xff1a; 笔者写过很多次这道题了&#xff0c;不想写题解了&#xff0c;大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

编程新知 2026/1/23 12:37:51

微服务商城-商品微服务

数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

编程新知 2026/1/29 18:30:30

什么是EULA和DPA

文章目录 EULA&#xff08;End User License Agreement&#xff09;DPA&#xff08;Data Protection Agreement&#xff09;一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA&#xff08;End User License Agreement&#xff09; 定义&#xff1a; EULA即…...

编程新知 2025/10/18 7:13:10

让AI看见世界：MCP协议与服务器的工作原理

让AI看见世界&#xff1a;MCP协议与服务器的工作原理 MCP&#xff08;Model Context Protocol&#xff09;是一种创新的通信协议&#xff0c;旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天&#xff0c;MCP正成为连接AI与现实世界的重要桥梁。…...

编程新知 2026/1/31 11:13:53

C# 求圆面积的程序（Program to find area of a circle）

给定半径r&#xff0c;求圆的面积。圆的面积应精确到小数点后5位。 例子&#xff1a; 输入&#xff1a;r 5 输出&#xff1a;78.53982 解释&#xff1a;由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982&#xff0c;因为我们只保留小数点后 5 位数字。 输…...

编程新知 2026/2/8 9:34:11

现有的 Redis 分布式锁库（如 Redisson）提供了哪些便利？

现有的 Redis 分布式锁库&#xff08;如 Redisson&#xff09;相比于开发者自己基于 Redis 命令&#xff08;如 SETNX, EXPIRE, DEL&#xff09;手动实现分布式锁&#xff0c;提供了巨大的便利性和健壮性。主要体现在以下几个方面&#xff1a; 原子性保证 (Atomicity)&#xff…...

编程新知 2025/9/23 11:26:04

AI+无人机如何守护濒危物种？YOLOv8实现95%精准识别

【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而&#xff0c;传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案&#xff0c;能够实现大范围覆盖并远程采集数据。尽管具备这些优势&#xf…...

编程新知 2026/1/26 12:50:00

在Mathematica中实现Newton-Raphson迭代的收敛时间算法（一般三次多项式）

考察一般的三次多项式&#xff0c;以r为参数&#xff1a; p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]&#xff1b; 此多项式的根为&#xff1a; 尽管看起来这个多项式是特殊的&#xff0c;其实一般的三次多项式都是可以通过线性变换化为这个形式…...

编程新知 2026/1/30 3:24:00

android13 app的触摸问题定位分析流程

一、知识点 一般来说，触摸问题都是app层面出问题，我们可以在ViewRootImpl.java添加log的方式定位；如果是touchableRegion的计算问题，就会相对比较麻烦了，需要通过adb shell dumpsys input > input.log指令，且通过打印堆栈的方式，逐步定位问题，并找到修改方案。 问题…...

编程新知 2026/1/31 13:18:31