代码随想录第45天 | 322. 零钱兑换、279. 完全平方数
322. 零钱兑换
动规五部曲分析如下:
-
确定dp数组以及下标的含义
dp[j]:凑足总额为j所需钱币的最少个数为dp[j] -
确定递推公式
凑足总额为j - coins[i]的最少个数为dp[j - coins[i]],那么只需要加上一个钱币coins[i]即dp[j - coins[i]] + 1就是dp[j](考虑coins[i])
所以dp[j] 要取所有 dp[j - coins[i]] + 1 中最小的。
递推公式:dp[j] = min(dp[j - coins[i]] + 1, dp[j]);
- dp数组如何初始化
首先凑足总金额为0所需钱币的个数一定是0,那么dp[0] = 0;
其他下标对应的数值呢?
考虑到递推公式的特性,dp[j]必须初始化为一个最大的数,否则就会在min(dp[j - coins[i]] + 1, dp[j])比较的过程中被初始值覆盖。
所以下标非0的元素都是应该是最大值。
- 确定遍历顺序
本题求钱币最小个数,那么钱币有顺序和没有顺序都可以,都不影响钱币的最小个数。
所以本题并不强调集合是组合还是排列。
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
/*** @param {number[]} coins* @param {number} amount* @return {number}*/
var coinChange = function (coins, amount) {const dp = Array(amount + 1).fill(Infinity)dp[0] = 0for (let i = 1; i <= amount; i++) {for (let j = 0; j < coins.length; j++) {if (i >= coins[j] && dp[i - coins[j]] !== Infinity) {dp[i] = Math.min(dp[i], dp[i - coins[j]] + 1)}}}return dp[amount] === Infinity ? -1 : dp[amount]
};
279. 完全平方数
-
确定dp数组(dp table)以及下标的含义
dp[j]:和为j的完全平方数的最少数量为dp[j] -
确定递推公式
dp[j] 可以由dp[j - i * i]推出, dp[j - i * i] + 1 便可以凑成dp[j]。
此时我们要选择最小的dp[j],所以递推公式:dp[j] = min(dp[j - i * i] + 1, dp[j]);
- dp数组如何初始化
dp[0]表示 和为0的完全平方数的最小数量,那么dp[0]一定是0。
有同学问题,那0 * 0 也算是一种啊,为啥dp[0] 就是 0呢?
看题目描述,找到若干个完全平方数(比如 1, 4, 9, 16, …),题目描述中可没说要从0开始,dp[0]=0完全是为了递推公式。
非0下标的dp[j]应该是多少呢?
从递归公式dp[j] = min(dp[j - i * i] + 1, dp[j]);中可以看出每次dp[j]都要选最小的,所以非0下标的dp[j]一定要初始为最大值,这样dp[j]在递推的时候才不会被初始值覆盖。
- 确定遍历顺序
我们知道这是完全背包,
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
/*** @param {number} n* @return {number}*/
var numSquares = function (n) {let dp = new Array(n + 1).fill(Infinity)dp[0] = 0for (let i = 1; i <= n; i++) {for (let j = 1; j * j <= i; j++) {dp[i] = Math.min(dp[i - j * j] + 1, dp[i])}}return dp[n]
};
相关文章:

代码随想录第45天 | 322. 零钱兑换、279. 完全平方数
322. 零钱兑换 动规五部曲分析如下: 确定dp数组以及下标的含义 dp[j]:凑足总额为j所需钱币的最少个数为dp[j] 确定递推公式 凑足总额为j - coins[i]的最少个数为dp[j - coins[i]],那么只需要加上一个钱币coins[i]即dp[j - coins[i]] 1就是…...

怎么加入Microsoft Cloud Partner Program?
目录 前言 加入Microsoft Cloud Partner Program 1、注册成为微软合作伙伴 2、完成合作伙伴资格要求...
LNMP简易搭建
目录 前言 一、拓扑图 二、NGINX配置 三、配置MySQL 四、配置php环境 五、部署应用 总结 前言 LNMP平台指的是将Linux、Nginx、MySQL和PHP(或者其他的编程语言,如Python、Perl等)集成在一起的一种Web服务器环境。它是一种常用的开发和部署网…...
CClink IE转Modbus TCP网关连接三菱FX5U PLC
捷米JM-CCLKIE-TCP 是自主研发的一款 CCLINK IE FIELD BASIC 从站功能的通讯网关。该产品主要功能是将各种 MODBUS-TCP 设备接入到 CCLINK IE FIELD BASIC 网络中。 捷米JM-CCLKIE-TCP网关连接到 CCLINK IE FIELD BASIC 总线中做为从站使用,连接到 MODBUS-TCP 总线…...

PyTorch 微调终极指南:第 1 部分 — 预训练模型及其配置
一、说明 如今,在训练深度学习模型时,通过在自己的数据上微调预训练模型来迁移学习已成为首选方法。通过微调这些模型,我们可以利用他们的专业知识并使其适应我们的特定任务,从而节省宝贵的时间和计算资源。本文分为四个部分&…...
GO学习之 微框架(Gin)
GO系列 1、GO学习之Hello World 2、GO学习之入门语法 3、GO学习之切片操作 4、GO学习之 Map 操作 5、GO学习之 结构体 操作 6、GO学习之 通道(Channel) 7、GO学习之 多线程(goroutine) 8、GO学习之 函数(Function) 9、GO学习之 接口(Interface) 10、GO学习之 网络通信(Net/Htt…...
C语言 字符指针
1、介绍 概念: 字符指针,就是字符类型的指针,同整型指针,指针指向的元素表示整型一样,字符指针指向的元素表示的是字符。 假设: char ch a;char * pc &ch; pc 就是字符指针变量,字符指…...

Springboot所有的依赖
<properties><maven.compiler.source>8</maven.compiler.source><maven.compiler.target>8</maven.compiler.target><project.build.sourceEncoding>UTF-8</project.build.sourceEncoding><!-- 声明springboot的版本号 -->…...
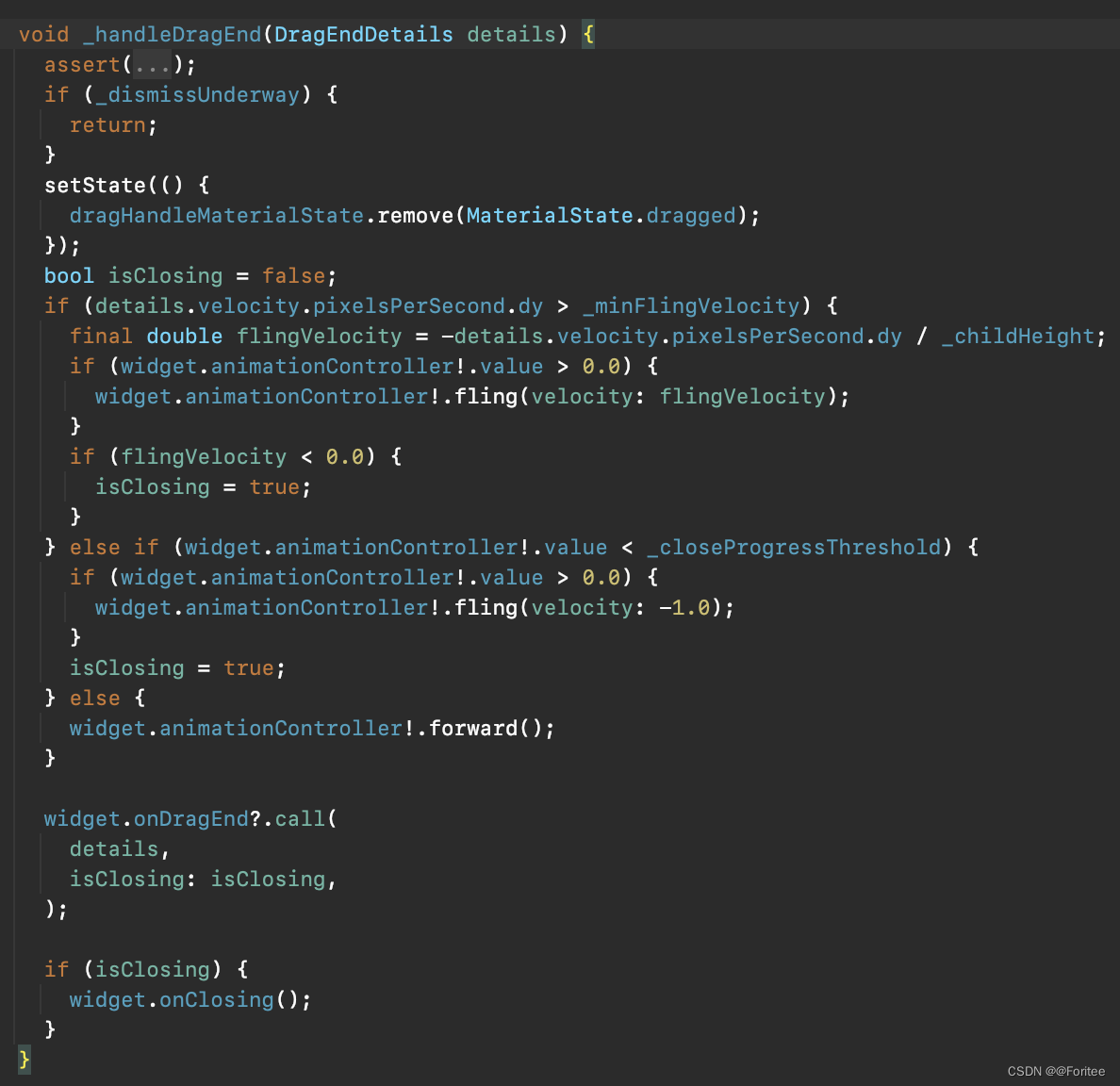
Flutter BottomSheet 三段式拖拽
BottomSheetBehavior 追踪 BottomSheet系统默认实现效果准备要实现的功能点:定义三段式状态:BottomSheetBehavoir阀值定义1. 未达到滚动阀值,恢复状态2. 达到滚动阀值,更新状态 前面倒是有讲过Android原生的BottomSheetBehavior&a…...
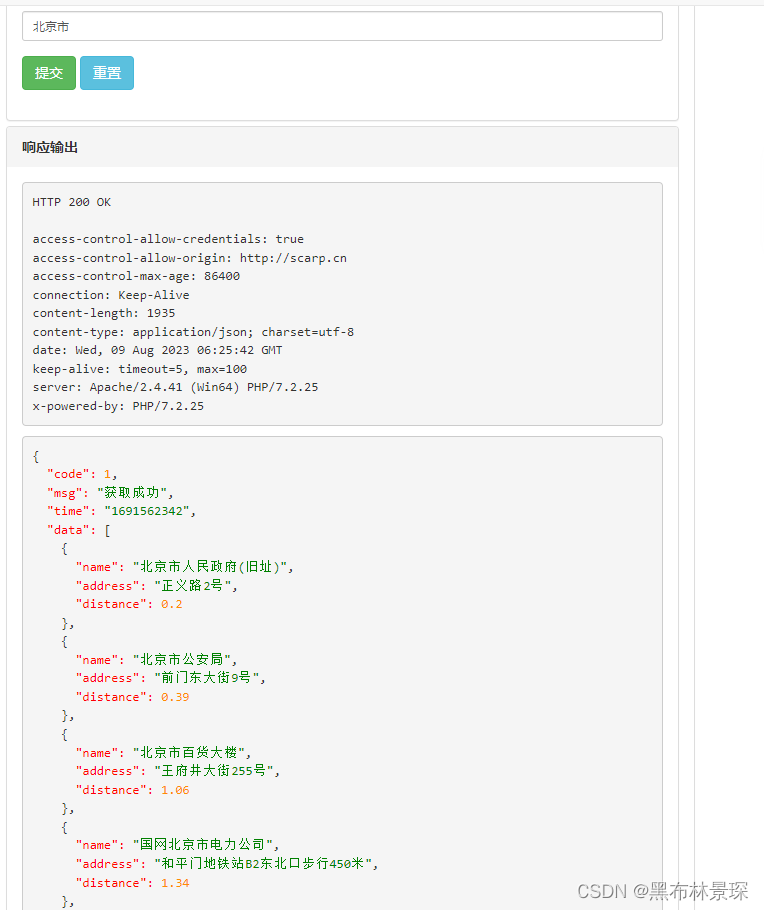
php后端实现调用高德地图进行POI搜索
对于当前位置或者选定省市位置进行查询 接口实现 /*** 查询地址* ApiTitle (查询地址)* ApiSummary (查询地址)* ApiMethod (POST)* ApiRoute (/api/demo/address)* ApiParams (name"dart", type"integer", requiredtrue, description"省…...
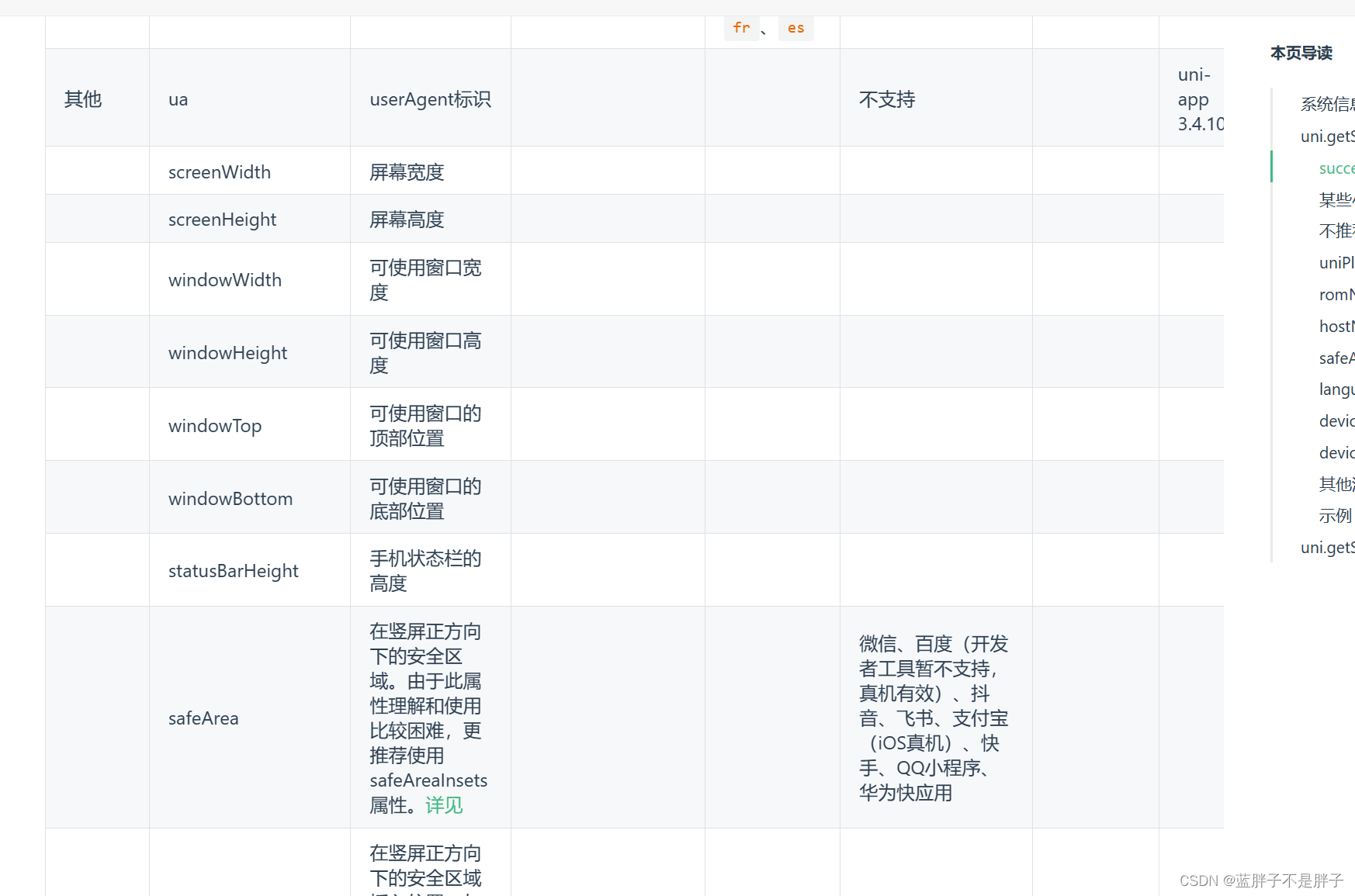
uniapp 实现滑动视图切换 顶部滚动导航栏
无论小程序的时候一般有这个功能,在页面处于首页时候,滑动视图,切换视图顶部滚动导航也跟着切换 1.想要实现这个功能就需要实现顶部导航栏,首先实现顶部滚导航栏 点击高亮颜色显示 模板代码 <scroll-view scroll-x"true" class"scroll-content" > …...

ArcGIS API for JavaScript 调用自定义地图模板总结
ArcGIS API for JavaScript 调用自定义地图模板总结 3.9版本4.24版本 3.9版本 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><title>Hello World</title><link rel"stylesheet" href&qu…...

QGraphicsView实现简易地图5『经纬网格』
前文链接:QGraphicsView实现简易地图4『局部加载-地图漫游』 由于GCJ02 Web 墨卡托投影 纬度并不随像素等分,且两极跨度较大,因此本次演示采用的经纬网等分逻辑为等分像素。同等像素跨度之间,两级纬度变化较小,越靠近赤…...
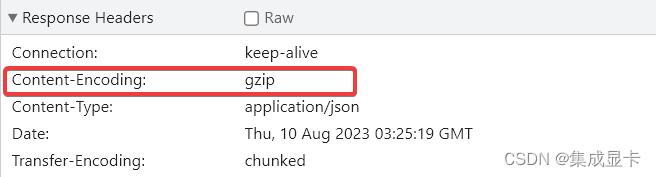
RestTemplate 请求转发异常 ERR_CONTENT_DECODING_FAILED 200 (OK)
#1 问题描述 在基于Spring Boot的项目中实现了请求转发(使用 RestTemplate 的 exchange 方法)的功能,忽然在前端报net::ERR_CONTENT_DECODING_FAILED 200 (OK)的错误,后端及上游系统日志均显示请求已完成。 #2 原因探寻 上述错…...

用python实现一个异或计算器
有这样一条需求:计算某个文件中的数组每一行元素的最后一个参数,异或输出。 因为元素比较多,十几行,通过人工去计算异或值非常困难。 而在线异或的计算器,也需要人为输入这些数值,每次计算一个最终结果需…...
Sketch打不开AI文件?转换方法在这里
1、对比设计软件 Sketch 与 AI 软件功能 Sketch 与 Illustrator 都是行业内优秀的矢量图形设计软件,各有千秋。Sketch 从 2010 年面世,专注 APP 界面设计,深受初学者与专业人士喜爱。Illustrator 拥有更悠久的历史,是处理复杂图标…...

小游戏扫雷实现教学(详解)
目录 【前言】 一、模块化程序设计(多文件编程)介绍 1.概述 2.传统编程的方式 3.模块化程序设计的方法 二、扫雷代码设计思路 三、扫雷代码设计 1.创建菜单函数 2.实现9x9扫雷 3.初始化棋盘 4.打印棋盘 5.随机布置雷的位置 6.排查雷的信息 7.回…...
04 mysql innodb record
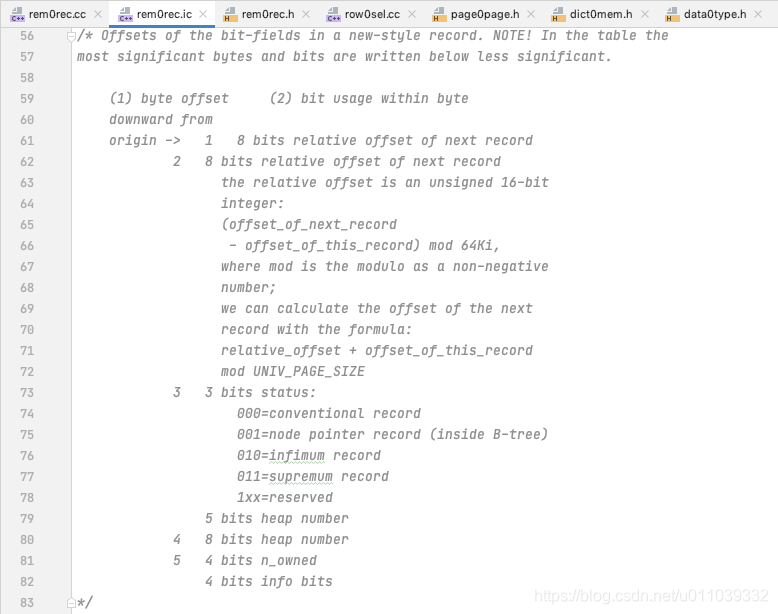
前言 最近看到了 何登成 大佬的 "深入MySQL源码 -- Step By Step" 的 pdf 呵呵 似乎是找到了一些 方向 之前对于 mysql 方面的东西, 更多的仅仅是简单的使用[业务中的各种增删改查], 以及一些面试题的背诵 这里会参照 MySQL Internals Manual 来大致的看一下 i…...

Centos7安装Docker
0.安装Docker Docker 分为 CE 和 EE 两大版本。CE 即社区版(免费,支持周期 7 个月),EE 即企业版,强调安全,付费使用,支持周期 24 个月。 Docker CE 分为 stable test 和 nightly 三个更新频道…...
Vue中如何更好地封装组件?
子组件接受父组件传递的事件 1.子组件使用事件名"$emit(父组件中传递的事件名,想给父组件传递的参数(可选))" click"$emit(click)" 2.子组件使用 v-on"$listeners" 父组件: <template><div id"app"><myCo…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...
的打车小程序)
基于鸿蒙(HarmonyOS5)的打车小程序
1. 开发环境准备 安装DevEco Studio (鸿蒙官方IDE)配置HarmonyOS SDK申请开发者账号和必要的API密钥 2. 项目结构设计 ├── entry │ ├── src │ │ ├── main │ │ │ ├── ets │ │ │ │ ├── pages │ │ │ │ │ ├── H…...

土建施工员考试:建筑施工技术重点知识有哪些?
《管理实务》是土建施工员考试中侧重实操应用与管理能力的科目,核心考查施工组织、质量安全、进度成本等现场管理要点。以下是结合考试大纲与高频考点整理的重点内容,附学习方向和应试技巧: 一、施工组织与进度管理 核心目标: 规…...
