LeetCode 周赛上分之旅 #39 结合中心扩展的单调栈贪心问题
⭐️ 本文已收录到 AndroidFamily,技术和职场问题,请关注公众号 [彭旭锐] 和 BaguTree Pro 知识星球提问。
学习数据结构与算法的关键在于掌握问题背后的算法思维框架,你的思考越抽象,它能覆盖的问题域就越广,理解难度也更复杂。在这个专栏里,小彭与你分享每场 LeetCode 周赛的解题报告,一起体会上分之旅。
本文是 LeetCode 上分之旅系列的第 39 篇文章,往期回顾请移步到文章末尾~
周赛 358
T1. 数组中的最大数对和(Easy)
- 标签:数学、分桶
T2. 翻倍以链表形式表示的数字(Medium)
- 标签:链表
T3. 限制条件下元素之间的最小绝对差(Medium)
- 标签:双指针、平衡树
T4. 操作使得分最大(Hard)
- 标签:贪心、排序、中心扩展、单调栈、快速幂

T1. 数组中的最大数对和(Easy)
https://leetcode.cn/problems/max-pair-sum-in-an-array/
题解一(分桶 + 数学)
- 枚举每个元素,并根据其最大数位分桶;
- 枚举每个分桶,计算最大数对和。
class Solution {
public:int maxSum(vector<int>& nums) {int U = 10;// 分桶vector<int> buckets[U];for (auto& e: nums) {int x = e;int m = 0;while (x > 0) {m = max(m, x % 10);x /= 10;}buckets[m].push_back(e);}// 配对int ret = -1;for (int k = 0; k < U; k++) {if (buckets[k].size() < 2) continue;sort(buckets[k].rbegin(), buckets[k].rend());ret = max(ret, buckets[k][0] + buckets[k][1]);}return ret;}
};
复杂度分析:
- 时间复杂度: O ( n l g n ) O(nlgn) O(nlgn) 瓶颈在排序,最坏情况下所有元素进入同一个分桶;
- 空间复杂度: O ( n ) O(n) O(n) 分桶空间;
题解二(一次遍历优化)
- 最大数对和一定是分桶中的最大两个数,我们只需要维护每个分桶的最大值,并在将新元素尝试加入分桶尝试更新结果。
class Solution {
public:int maxSum(vector<int>& nums) {int U = 10;int ret = -1;int buckets[U];memset(buckets, -1, sizeof(buckets));for (auto& e: nums) {int x = e;int m = 0;while (x > 0) {m = max(m, x % 10);x /= 10;}if (-1 != buckets[m]) {ret = max(ret, buckets[m] + e);}buckets[m] = max(buckets[m], e);}return ret;}
};
复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n) 线性遍历;
- 空间复杂度: O ( U ) O(U) O(U) 分桶空间。
T2. 翻倍以链表形式表示的数字(Medium)
https://leetcode.cn/problems/double-a-number-represented-as-a-linked-list/
题解一(模拟)
面试类型题,有 O ( 1 ) O(1) O(1) 空间复杂度的写法:
- 先反转链表,再依次顺序翻倍,最后再反转回来;
- 需要注意最后剩余一个进位的情况需要补足节点。
class Solution {fun doubleIt(head: ListNode?): ListNode? {// 反转val p = reverse(head)// 翻倍var cur = pvar append = 0while (cur != null) {append += cur.`val` * 2cur.`val` = append % 10append = append / 10cur = cur.next}// 反转if (0 == append) return reverse(p)return ListNode(append).apply {next = reverse(p)}}fun reverse(head: ListNode?): ListNode? {var p: ListNode? = nullvar q = headwhile (null != q) {val next = q.nextq.next = pp = qq = next}return p}
}
复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n) 反转与翻倍是线性时间复杂度;
- 空间复杂度: O ( 1 ) O(1) O(1) 仅使用常量级别空间。
题解二(一次遍历优化)
我们发现进位只发生在元素值大于 4 的情况,我们可以提前观察当前节点的后继节点的元素值是否大于 4,如果是则增加进位 1。特别地,当首个元素大于 4 时需要补足节点。
class Solution {fun doubleIt(head: ListNode?): ListNode? {if (head == null) return null// 补足val newHead = if (head.`val` > 4) {ListNode(0).also { it.next = head}} else {head}// 翻倍var cur: ListNode? = newHeadwhile (null != cur) {cur.`val` *= 2if ((cur?.next?.`val` ?: 0) > 4) cur.`val` += 1cur.`val` %= 10cur = cur.next}return newHead}
}
复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n) 线性遍历;
- 空间复杂度: O ( 1 ) O(1) O(1) 仅使用常量级别空间。
相似题目:
- 445. 两数相加 II
T3. 限制条件下元素之间的最小绝对差(Medium)
https://leetcode.cn/problems/minimum-absolute-difference-between-elements-with-constraint/
题解(双指针 + 平衡树 )
- 滑动窗口的变型题,常规的滑动窗口是限定在窗口大小在 x 内,而这道题是排除到窗口外。万变不离其宗,还得是双指针。
- 其次,为了让元素配对的差值绝对值尽可能小,应该使用与其元素值相近最大和最小的两个数,可以用平衡树在 O(lgn) 时间复杂度内求得,整体时间复杂度是 O(ngln);
class Solution {fun minAbsoluteDifference(nums: List<Int>, x: Int): Int {if (x == 0) return 0 // 特判var ret = Integer.MAX_VALUEval n = nums.sizeval set = TreeSet<Int>()for (i in x until n) {// 滑动set.add(nums[i - x])val q = set.floor(nums[i])val p = set.ceiling(nums[i])if (p != null) ret = Math.min(ret, Math.abs(p - nums[i]))if (q != null) ret = Math.min(ret, Math.abs(nums[i] - q))}return ret }
}
复杂度分析:
- 时间复杂度: O ( m l g m ) O(mlgm) O(mlgm) 其中 m = n - x,内层循环二分搜索的时间复杂度是 O ( l g m ) O(lgm) O(lgm);
- 空间复杂度: O ( m ) O(m) O(m) 平衡树空间。
T4. 操作使得分最大(Hard)
https://leetcode.cn/problems/apply-operations-to-maximize-score/
题解一(贪心 + 排序 + 中心扩展 + 单调栈 + 快速幂)
这道题难度不算高,但使用到的技巧还挺综合的。
-
阅读理解: 可以得出影响结果 3 点关键信息,我们的目标是选择 k 个子数组,让其中质数分数最大的元素 nums[i] 尽量大:
- 1、元素大小
- 2、元素的质数分数
- 3、左边元素的优先级更高
-
预处理: 先预处理数据范围内每个数的质数分数,避免在多个测试用例间重复计算;
-
质因数分解: 求解元素的质数分数需要质因数分解,有两种写法:
-
暴力写法,时间复杂度 O ( n ⋅ n ) O(n·\sqrt{n}) O(n⋅n):
val scores = IntArray(U + 1) for (e in 1 .. U) {var cnt = 0var x = evar prime = 2while (prime * prime <= x) {if (x % prime == 0) {cnt ++while (x % prime == 0) x /= prime // 消除相同因子}prime++}if (x > 1) cnt ++ // 剩余的质因子scores[e] = cnt } -
基于质数筛写法,时间复杂度 O(n):
val scores = IntArray(U + 1) for (i in 2 .. U) {if (scores[i] != 0) continue // 合数for (j in i .. U step i) {scores[j] += 1} }
-
-
排序: 根据关键信息 「1、元素大小」 可知,我们趋向于选择包含较大元素值的子数组,且仅包含数组元素最大值的子数组是子数组分数的上界;
-
中心扩展: 我们先对所有元素降序排序,依次枚举子数组,计算该元素对结果的贡献,直到该元素无法构造更多子数组。以位置 i 为中心向左右扩展,计算左右两边可以记入子数组的元素个数 leftCnt 和 rightCnt。另外,根据 「左边元素的优先级更高」 的元素,向左边扩展时不能包含质数分数相同的位置,向右边扩展时可以包含;
-
乘法原理: 包含元素 nums[i] 的子数组个数满足乘法法则(leftCnt * rightCnt);
-
单调栈: 在中心扩展时,我们相当于在求 「下一个更大值」元素,这是典型的 单调栈问题,可以在 O ( n ) O(n) O(n) 时间复杂度内求得所有元素的下一个更大值;
val stack = ArrayDeque<Int>() for (i in 0 until n) {while (!stack.isEmpty() && nums[stack.peek()] < nums[i]) {stack.pop()}stack.push(i) } -
快速幂: 三种写法:
-
暴力写法,时间复杂度 O(n),由于题目 k 比较大会超出时间限制:
fun pow(x: Int, n: Int, mod: Int): Int {var ret = 1Lrepeat (n){ret = (ret * x) % mod}return ret.toInt() } -
分治写法,时间复杂度是 O(lgn):
fun pow(x: Int, n: Int, mod: Int): Int {if (n == 1) return xval subRet = pow(x, n / 2, mod)return if (n % 2 == 1) {1L * subRet * subRet % mod * x % mod} else {1L * subRet * subRet % mod}.toInt() } -
快速幂写法,时间复杂度 O©:
private fun quickPow(x: Int, n: Int, mod: Int): Int {var ret = 1Lvar cur = nvar k = x.toLong()while (cur > 0) {if (cur % 2 == 1) ret = ret * k % modk = k * k % modcur /= 2}return ret.toInt() }
-
组合以上技巧:
class Solution {companion object {private val MOD = 1000000007private val U = 100000private val scores = IntArray(U + 1)init {// 质数筛for (i in 2 .. U) {if (scores[i] != 0) continue // 合数for (j in i .. U step i) {scores[j] += 1}}}}fun maximumScore(nums: List<Int>, k: Int): Int {val n = nums.size// 贡献(子数组数)val gains1 = IntArray(n) { n - it }val gains2 = IntArray(n) { it + 1}// 下一个更大的分数(单调栈,从栈底到栈顶单调递减)val stack = ArrayDeque<Int>()for (i in 0 until n) {while (!stack.isEmpty() && scores[nums[stack.peek()]] < scores[nums[i]]) {val j = stack.pop()gains1[j] = i - j}stack.push(i)}// 上一个更大元素(单调栈,从栈底到栈顶单调递减)stack.clear()for (i in n - 1 downTo 0) {while(!stack.isEmpty() && scores[nums[stack.peek()]] <= scores[nums[i]]) { // <=val j = stack.pop()gains2[j] = j - i}stack.push(i)}// 按元素值降序val ids = Array<Int>(n) { it }Arrays.sort(ids) { i1, i2 ->nums[i2] - nums[i1]}// 枚举每个元素的贡献度var leftK = kvar ret = 1Lfor (id in ids.indices) {val gain = Math.min(gains1[ids[id]] * gains2[ids[id]], leftK)ret = (ret * quickPow(nums[ids[id]], gain, MOD)) % MODleftK -= gainif (leftK == 0) break}return ret.toInt()}// 快速幂private fun quickPow(x: Int, n: Int, mod: Int): Int {var ret = 1Lvar cur = nvar k = x.toLong()while (cur > 0) {if (cur % 2 == 1) ret = ret * k % modk = k * k % modcur /= 2}return ret.toInt()}
}
复杂度分析:
- 时间复杂度: O ( n l g n ) O(nlgn) O(nlgn) 其中预处理时间为 O ( U ) O(U) O(U),单次测试用例中使用单调栈计算下一个更大质数分数的时间为 O ( n ) O(n) O(n),排序时间为 O ( n l g n ) O(nlgn) O(nlgn),枚举贡献度时间为 O ( n ) O(n) O(n),整体瓶颈在排序;
- 空间复杂度: O ( n ) O(n) O(n) 预处理空间为 O ( U ) O(U) O(U),单次测试用例中占用 O ( n ) O(n) O(n) 空间。
题解二(一次遍历优化)
在计算下一个更大元素时,在使用 while 维护单调栈性质后,此时栈顶即为当前元素的前一个更大元素:
while (!stack.isEmpty() && nums[stack.peek()] < nums[i]) {stack.pop()
}
// 此时栈顶即为当前元素的前一个更大元素
stack.push(i)
因此我们可以直接在一次遍历中同时计算出前一个更大元素和下一个更大元素:
val right = IntArray(n) { n } // 下一个更大元素的位置
val left = IntArray(n) { -1 } // 上一个更大元素的位置
计算贡献度的方法: ( i − l e f t [ i ] ) ∗ ( r i g h t [ i ] − i ) (i - left[i]) * (right[i] - i) (i−left[i])∗(right[i]−i),其中 l e f t [ i ] left[i] left[i] 和 r i g h t [ i ] right[i] right[i] 位置不包含在子数组中。
class Solution {...fun maximumScore(nums: List<Int>, k: Int): Int {val n = nums.size// 贡献(子数组数)val right = IntArray(n) { n } // 下一个更大元素的位置val left = IntArray(n) { -1 } // 上一个更大元素的位置// 下一个更大的分数(单调栈,从栈底到栈顶单调递减)val stack = ArrayDeque<Int>()for (i in 0 until n) {while (!stack.isEmpty() && scores[nums[stack.peek()]] < scores[nums[i]]) {right[stack.pop()] = i // 下一个更大元素的位置}if (!stack.isEmpty()) left[i] = stack.peek() // 上一个更大元素的位置stack.push(i)}// 按元素值降序val ids = Array<Int>(n) { it }Arrays.sort(ids) { i1, i2 ->nums[i2] - nums[i1]}// 枚举每个元素的贡献度val gains = IntArray(n) { (it - left[it]) * (right[it] - it)}var leftK = kvar ret = 1Lfor (id in ids.indices) {val gain = Math.min(gains[ids[id]], leftK)ret = (ret * quickPow(nums[ids[id]], gain, MOD)) % MODleftK -= gainif (leftK == 0) break}return ret.toInt()}...
}
复杂度分析:
- 同上
相似题目:
- 907. 子数组的最小值之和
- 1856. 子数组最小乘积的最大值
- 2104. 子数组范围和
- 2281. 巫师的总力量和
推荐阅读
LeetCode 上分之旅系列往期回顾:
- LeetCode 单周赛第 358 场 · 结合排序不等式的动态规划
- LeetCode 单周赛第 357 场 · 多源 BFS 与连通性问题
- LeetCode 双周赛第 109 场 · 按部就班地解决动态规划问题
- LeetCode 双周赛第 107 场 · 很有意思的 T2 题
⭐️ 永远相信美好的事情即将发生,欢迎加入小彭的 Android 交流社群~

相关文章:

LeetCode 周赛上分之旅 #39 结合中心扩展的单调栈贪心问题
⭐️ 本文已收录到 AndroidFamily,技术和职场问题,请关注公众号 [彭旭锐] 和 BaguTree Pro 知识星球提问。 学习数据结构与算法的关键在于掌握问题背后的算法思维框架,你的思考越抽象,它能覆盖的问题域就越广,理解难度…...

山东布谷科技直播软件开发WebRTC技术:建立实时通信优质平台
在数字化的时代,实时通信成为了人们远程交流的主要方式,目前市场上也出现了很多带有实时通信交流的软件,实时通信符合人们现在的需求,所以在直播软件开发过程中,开发者也运用了实时通信技术为直播软件加入了实时通信的…...

Golang-语言源码级调试器 Delve
前言 Go 目前的调试器有如下几种: GDB 最早期的调试工具,现在用的很少。LLDB macOS 系统推荐的标准调试工具,单 Go 的一些专有特性支持的比较少。Delve 专门为 Go 语言打造的调试工具,使用最为广泛。 本篇简单说明如何使用 Del…...
构建Docker容器监控系统(Cadvisor +InfluxDB+Grafana)
目录 案例概述 Cadvisor InfluxDBGrafana 1.1、 Cadvisor 1.2、InfluxDB 1.3、Grafana 1.4、监控组件架构 1.5、开始部署 安装docker-ce 阿里云镜像加速器 创建自定义网络 创建influxdb容器 案例概述 Docker作为目前十分出色的容器管理技术,得到大量企业…...
【Vue3】keep-alive 缓存组件
当在 Vue.js 中使用 <keep-alive> 组件时,它将会缓存动态组件,而不是每次渲染都销毁和重新创建它们。这对于需要在组件间快速切换并且保持组件状态的情况非常有用。 <keep-alive> 只能包含(或者说只能渲染)一个子组件…...

24成都信息工程大学809软件工程考研
1.渐增式与非渐增式各有何优、缺点?为什么通常采用渐增式? 非渐增式是将所有的模块一次连接起来,简单、易行、节省机时,但测试过程难于排错,发现错误也很难定位,测试效率低;渐增式是将模块一个…...

Filament for Android 编译搭建(基于Ubuntu20.04系统)
一、Filament 源代码下载 github下载地址: 2、安装clang 我是直接安装clang-10 Ubuntu 20.04 ,sudo apt install clang 命令默认就是clang-10 $sudo apt-get install clang-10 # 安装 AST.h 等头文件 $sudo apt-get install libclang-10-dev $sudo …...

【MySQL--->数据库操作】
文章目录 [TOC](文章目录) 一、操作语句1.增2.删3.改4.查5.备份 二、字符集与校验规则 一、操作语句 1.增 语句格式:create database [if no exists]数据库名[create_specification [,create_specification] …]; 中括号内是可选项,if no exists是指如果数据库不存在就创建,存…...

PhotoShop2023 Beta AI版安装教程
从 Photoshop 开始,惊艳随之而来 从社交媒体贴子到修饰相片,设计横幅到精美网站,日常影像编辑到重新创造 – 无论什么创作,Photoshop 都可以让它变得更好。 Photoshop2023 Beta版本安装教程和软件下载 地址:点击…...

并发冲突导致流量放大的线上问题解决
事故现象 生产环境,转账相关请求失败量暴增。 直接原因 现网多个重试请求同时到达 svr,导致内存数据库大量返回时间戳冲突。业务方收到时间戳冲突,自动进行业务重试,服务内部也存在重试,导致流量放大。 转账 首先…...
Spring Cloud Gateway过滤器GlobalFilter详解
一、过滤器的场景 在springCloud架构中,网关是必不可少的组件,它用于服务路由的转发。对客户端进行屏蔽微服务的具体细节,客户端只需要和网关进行交互。所以网关顾名思义,就是网络的一个关卡。它就是一座城的城门守卫。所以这个守…...

【LeetCode】1281.整数的各位积和之差
题目 给你一个整数 n,请你帮忙计算并返回该整数「各位数字之积」与「各位数字之和」的差。 示例 1: 输入:n 234 输出:15 解释: 各位数之积 2 * 3 * 4 24 各位数之和 2 3 4 9 结果 24 - 9 15示例 2&…...
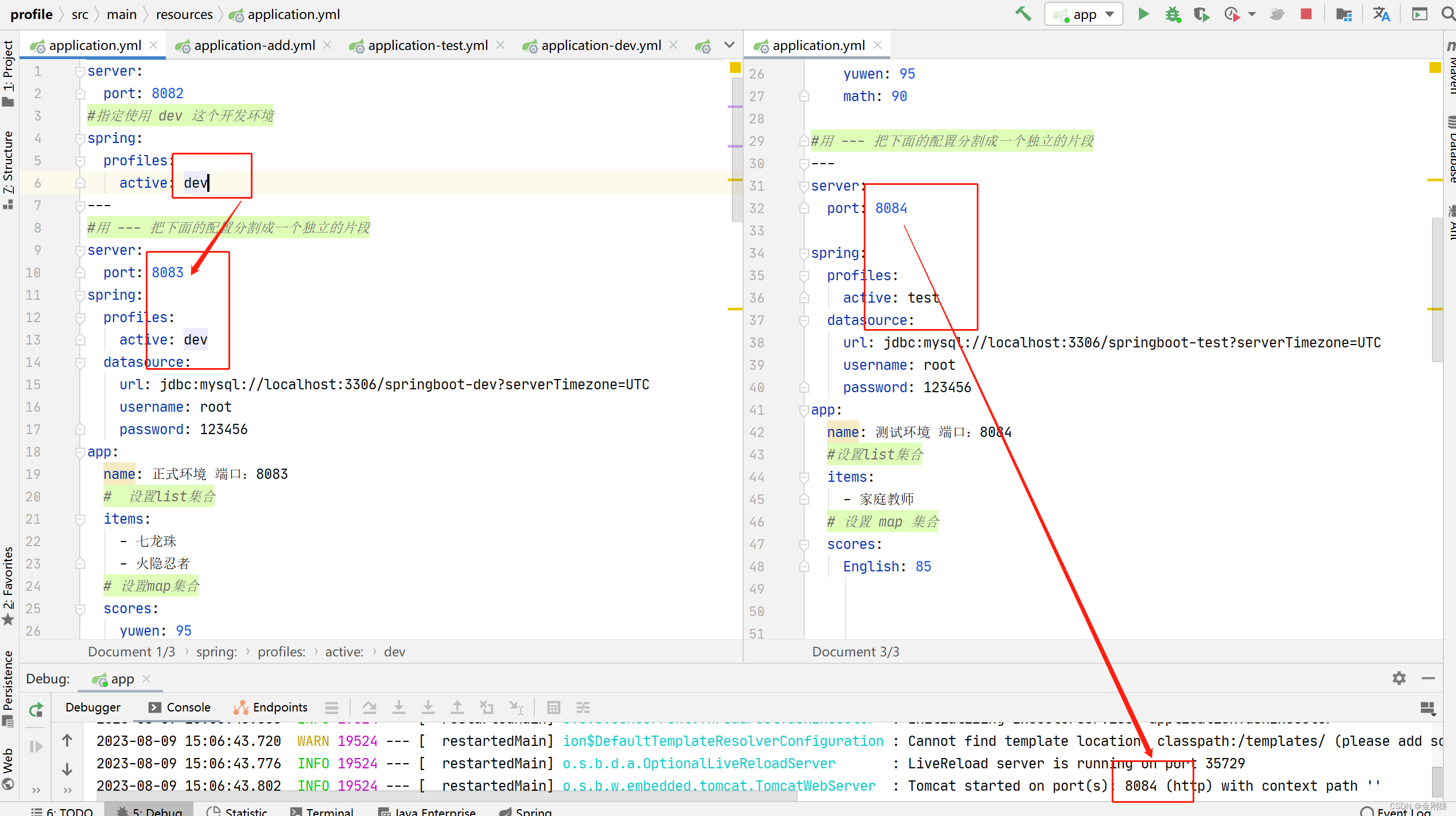
22、springboot的Profile(通过yml配置文件配置 profile,快速切换项目的开发环境)
springboot的Profile ★ 何谓Profile 应用所在的运行环境发生切换时,配置文件常常就需要随之修改。Profile:——就是一组配置文件及组件的集合。可以整个应用在不同的profile之间切换(设置活动profile),整个应用都将使…...

2023-08-12力扣每日一题-暴力hard
链接: 23. 合并 K 个升序链表 题意: 如题 解: 时间668ms击败 5.00%使用 C 的用户/内存12.37mb击败 87.96%使用 C 的用户 循环选择插入新链表的节点,纯正的暴力,不过空间用得少 最坏应该是1E4*1E4,没…...

Mac安装nvm教程及使用
nvm 是 node 版本管理器,也就是说一个 nvm 可以管理多个 node 版本(包含 npm 与 npx),可以方便快捷的安装、切换 不同版本的 node。 1、直接通过brew安装 执行命令:brew install nvm PS: 如果没有安装br…...

左值引用和右值引用
目录 辨析引用和指针 代码段 定义引用变量的技巧 同一内存 指针和引用的简单运用 辨析两类指针 数组、指针、引用 辨析左值引用和右值引用 代码段 左值引用和右值引用 辨析引用和指针 1、引用是一种更安全的指针 说明:引用必须初始化,而指针可…...

JavaWeb 中对 HTTP 协议的学习
HTTP1 Web概述1.1 Web和JavaWeb的概念1.2 JavaWeb技术栈1.2.1 B/S架构1.2.2 静态资源1.2.3 动态资源1.2.4 数据库1.2.5 HTTP协议1.2.6 Web服务器 1.3 Web核心 2 HTTP2.1 简介2.2 请求数据格式2.2.1 格式介绍2.2.2 实例演示 2.3 响应数据格式2.3.1 格式介绍2.3.2 响应状态码2.3.…...
)
06-hadoop集群搭建(root用户)
搭建Hadoop集群流程 环境准备 1、基础环境的搭建(内网封火墙关闭、主机名、规划好静态ip、hosts映射、时间同步ntp、jdk、ssh免密等) 2、Hadoop源码编译(为了适应不同操作系统间适配本地库、本地环境等) 3、Hadoop配置文件的修…...

MySQL 窗口函数是什么,有这么好用
先看这段像天书一样的 SQL ,看着就头疼。 SELECTs1.name,s1.subject,s1.score,sub.avg_score AS average_score_per_subject,(SELECT COUNT(DISTINCT s2.score) 1 FROM scores s2 WHERE s2.score > s1.score) AS score_rank FROM scores s1 JOIN (SELECT subject, AVG(sco…...
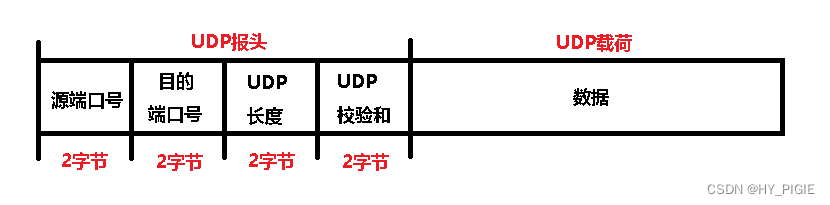
用户数据报协议UDP
UDP的格式 载荷存放的是:应用层完整的UDP数据报 报头结构: 源端口号:发出的信息的来源端口目的端口号:信息要到达的目的端口UDP长度:2个字节(16位),即UDP总长度为:2^16bit 2^10bit * 2^6bit 1KB * 64 64KB.所以一个UDP的最大长度为64KBUDP校验和:网络的传输并非稳定传输,…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

SQL Server 触发器调用存储过程实现发送 HTTP 请求
文章目录 需求分析解决第 1 步:前置条件,启用 OLE 自动化方式 1:使用 SQL 实现启用 OLE 自动化方式 2:Sql Server 2005启动OLE自动化方式 3:Sql Server 2008启动OLE自动化第 2 步:创建存储过程第 3 步:创建触发器扩展 - 如何调试?第 1 步:登录 SQL Server 2008第 2 步…...
