【2023】字节跳动 10 日心动计划——第九关
目录
- 1. 螺旋矩阵
- 2. 划分字母区间
- 3. 子集 II
1. 螺旋矩阵
🔗 原题链接:54. 螺旋矩阵
类似于BFS那样使用方向数组即可。
class Solution {
public:vector<int> spiralOrder(vector<vector<int>>& matrix) {int m = matrix.size(), n = matrix[0].size();int dx[] = {-1, 0, 1, 0}, dy[] = {0, 1, 0, -1};vector<int> ans;int x = 0, y = 0, d = 1;ans.push_back(matrix[x][y]);for (int i = 0; i < n * m - 1; i++) {matrix[x][y] = -101;int a = x + dx[d], b = y + dy[d];if (a < 0 || a >= m || b < 0 || b >= n || matrix[a][b] == -101) {d = (d + 1) % 4;a = x + dx[d], b = y + dy[d];}x = a, y = b;ans.push_back(matrix[x][y]);}return ans;}
};
2. 划分字母区间
🔗 原题链接:763. 划分字母区间
这题本质是一个模拟题。
题目中规定了同一个字符不能出现在多个区间中,因此对于一个字符而言,如果它包含于某个区间,那么这个区间应当包含所有这样的字符。例如,如果一个区间包含字符 a,那么这个区间至少是 [a第一次出现的下标, a最后一次出现的下标]。这里为什么要用「至少」?是因为这个区间还会包含其他的字符,我们还需要对其他字符反复应用上述过程直到区间不再更新。
由于题目中的区间是按顺序分割的,因此我们只需要维护每个字符最后一次出现的下标即可。
例如对于字符串 ababcbacadefegdehijhklij,我们先看第一个字符 a,该字符最后一次出现的下标为 8 8 8,说明第一个区间至少是 [ 0 , 8 ] [0,8] [0,8]。我们依次枚举该区间的每一个字符,并用字符最后一次出现的下标来更新区间的右端点,这样一来,我们就可以得到不可分割的第一个区间。事实上,第一个区间就是 [ 0 , 8 ] [0,8] [0,8]。
现在从下标为 9 9 9 的地方开始,该下标对应的字符是 d,该字符最后一次出现的下标为 14 14 14,说明第二个区间至少是 [ 9 , 14 ] [9,14] [9,14],但注意到这个区间中有一个字符 e,所以我们必须扩充区间来把所有的 e 都包含进来,最终得到第二个区间为 [ 9 , 15 ] [9,15] [9,15]。
类似可得到第三个区间 [ 16 , 23 ] [16,23] [16,23]。
最终答案就是 [ 8 − 0 + 1 , 15 − 9 + 1 , 23 − 16 + 1 ] = [ 9 , 7 , 8 ] [8-0+1,15-9+1,23-16+1]=[9,7,8] [8−0+1,15−9+1,23−16+1]=[9,7,8]。
class Solution {
public:vector<int> partitionLabels(string s) {unordered_map<char, int> last;for (int i = 0; i < s.size(); i++) last[s[i]] = i;vector<int> res;int start = 0, end = 0;for (int i = 0; i < s.size(); i++) {end = max(end, last[s[i]]);if (i == end) {res.push_back(end - start + 1);start = end = i + 1;}}return res;}
};
3. 子集 II
🔗 原题链接:90. 子集 II
回顾全排列 I,我们是先枚举每个位置(通过 u u u 来控制),然后再枚举每个位置能够选哪些数。
回顾子集 I,我们同样是枚举每个位置,然后再枚举这个位置到底是选还是不选。
回顾全排列 II,我们的枚举思路和全排列 I相同,但是为了避免重复,我们固定了相同数字的相对位置。
回到本题,为了避免重复,我们同样可以先对数组排个序以确保相同的数字相邻,然后枚举每个位置,对于每个位置,枚举这个位置上对应的数可能出现的次数,即 [ 0 , k ] , k ≥ 1 [0,k],\,k\geq 1 [0,k],k≥1。当 k = 1 k=1 k=1 时,子集 II就退化成了子集 I。
class Solution {
public:vector<vector<int>> ans;vector<int> path;vector<vector<int>> subsetsWithDup(vector<int>& nums) {sort(nums.begin(), nums.end());dfs(nums, 0);return ans;}void dfs(vector<int>& nums, int u) {if (u == nums.size()) {ans.push_back(path);return;}int k = u;while (k < nums.size() && nums[k] == nums[u]) k++;// 选0个dfs(nums, k);// 选1到k-u个for (int i = 0; i < k - u; i++) {path.push_back(nums[u]);dfs(nums, k);}path.erase(path.end() - (k - u), path.end());}
};
如果把递归过程看作在递归搜索树上游走,那么执行一次 dfs(nums, u) 相当于在当前节点处创建一个第 u u u 层的子节点,然后移动到该子节点。当 dfs(nums, u) 执行完后,会返回到当前节点。
我们还需要保持dfs的前后状态一致。即执行dfs前的状态是什么样的,执行dfs后的状态也应当是什么样的。例如,我们通常喜欢在dfs之前修改 path 变量,那么在dfs执行之后,path 应当恢复成原来的样子,这一动作又称「恢复现场」。如果不想恢复现场,我们可以将 path 作为dfs函数的参数,在调用dfs的时候直接修改实参 path 即可(通常当 path 为字符串的时候会用到这种做法)。
可能会有读者好奇,为什么上述dfs函数中的for循环体中,没有在最后执行 path.pop_back() 呢?这是因为我们要枚举当前元素选 1 ∼ k − u 1\sim k-u 1∼k−u 个的情形,如果dfs后执行了 pop_back(),那么回到了当前节点后 path 就是空的,下次再dfs的时候 path 中仍然只有一个元素,这与 path 中应当有两个元素不符,所以我们应当等所有dfs执行完后统一恢复现场。
如果上述的C++代码还不够直观,那么请参考下方的Python实现:
class Solution:def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:def dfs(nums: List[int], u: int, path: List[int]):if u == len(nums):ans.append(path.copy())returnk = uwhile k < len(nums) and nums[k] == nums[u]:k += 1# 选0个dfs(nums, k, path)# 选1~k-u个for i in range(k - u):dfs(nums, k, path + [nums[u]] * (i + 1))nums.sort()ans = []dfs(nums, 0, [])return ans
因为Python可以直接在实参中修改列表,所以我们不需要做恢复现场,代码看起来也更加具有可读性。
注意到在C++中我们可以把选0个和选1~k-u个统一起来,即:
void dfs(vector<int>& nums, int u) {if (u == nums.size()) {ans.push_back(path);return;}int k = u;while (k < nums.size() && nums[k] == nums[u]) k++;for (int i = 0; i < k - u + 1; i++) {dfs(nums, k);path.push_back(nums[u]);}path.erase(path.end() - (k - u + 1), path.end());
}
在for循环中,交换dfs和push_back的顺序,那么第一次循环的时候就代表选0个。
注意到 n u m s [ i ] ∈ [ − 10 , 10 ] nums[i]\in[-10,10] nums[i]∈[−10,10],我们可以从另一种角度来进行dfs:
class Solution {
public:unordered_map<int, int> cnt;vector<vector<int>> ans;vector<int> path;vector<vector<int>> subsetsWithDup(vector<int>& nums) {for (auto num: nums) cnt[num]++;dfs(-10);return ans;}void dfs(int u) {if (u > 10) {ans.push_back(path);return;}for (int i = 0; i < cnt[u] + 1; i++) {dfs(u + 1);path.push_back(u);}path.erase(path.end() - (cnt[u] + 1), path.end());}
};
相关文章:

【2023】字节跳动 10 日心动计划——第九关
目录 1. 螺旋矩阵2. 划分字母区间3. 子集 II 1. 螺旋矩阵 🔗 原题链接:54. 螺旋矩阵 类似于BFS那样使用方向数组即可。 class Solution { public:vector<int> spiralOrder(vector<vector<int>>& matrix) {int m matrix.size(), …...
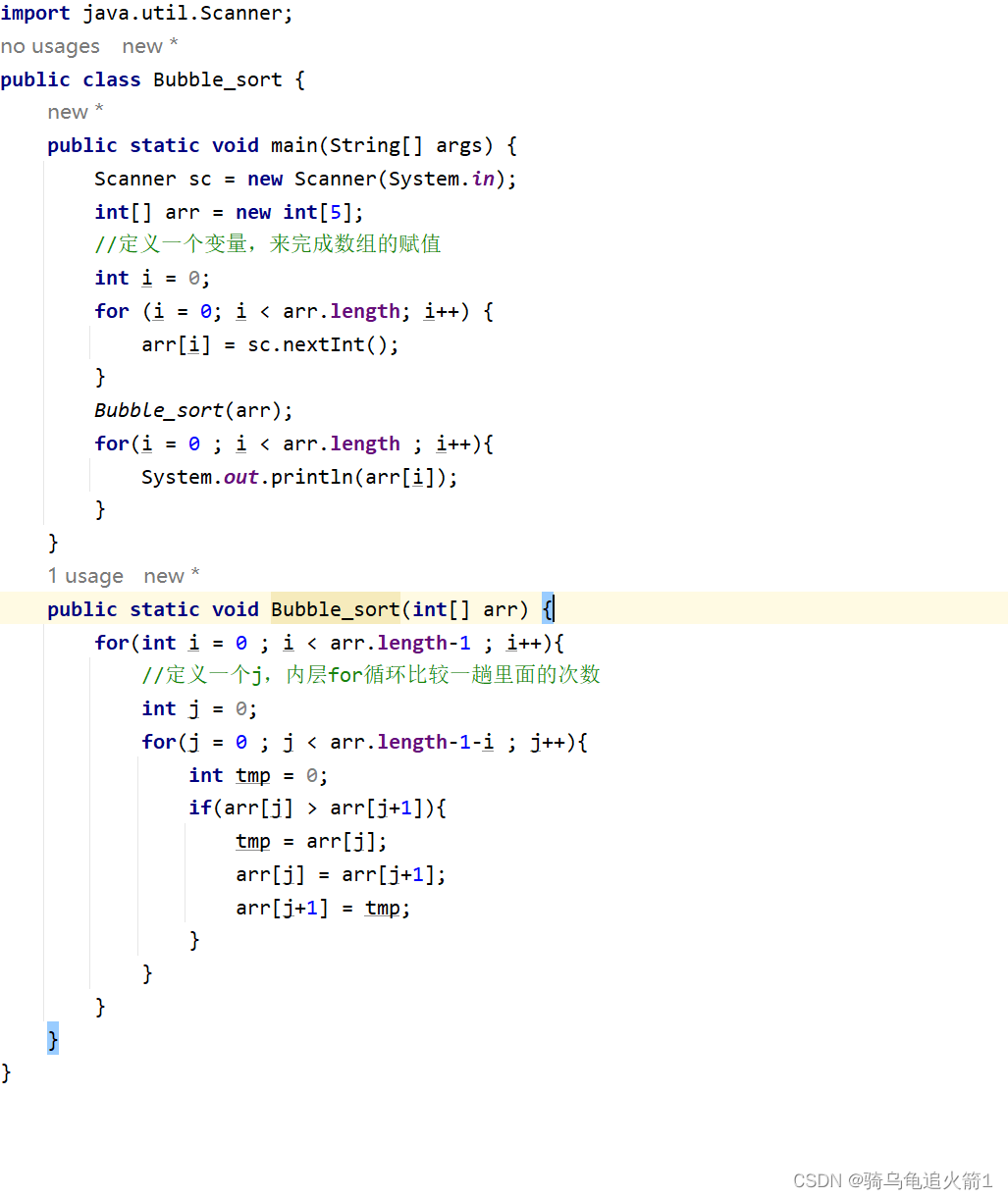
小龟带你敲排序之冒泡排序
冒泡排序 一. 定义二.题目三. 思路分析(图文结合)四. 代码演示 一. 定义 冒泡排序(Bubble Sort,台湾译为:泡沫排序或气泡排序)是一种简单的排序算法。它重复地走访过要排序的数列,一次比较两个元…...
Nacos AP架构集群搭建(Windows)
手写SpringCloud项目地址,求个star github:https://github.com/huangjianguo2000/spring-cloud-lightweight gitee:https://gitee.com/huangjianguo2000/spring-cloud-lightweigh 目录: 一:初始化MySQL 二:复制粘贴三份Nacos文…...

nodejs+vue+elementui,图书评论管理系统_g9e3a
用户的功能主要是对首页、图书信息、公告信息、在线咨询、个人中心等进行操作。表名:token语言 node.js 框架:Express 前端:Vue.js 数据库:mysql 数据库工具:Navicat 开发软件:VScode 前端nodejsvueelementui, 管理员…...
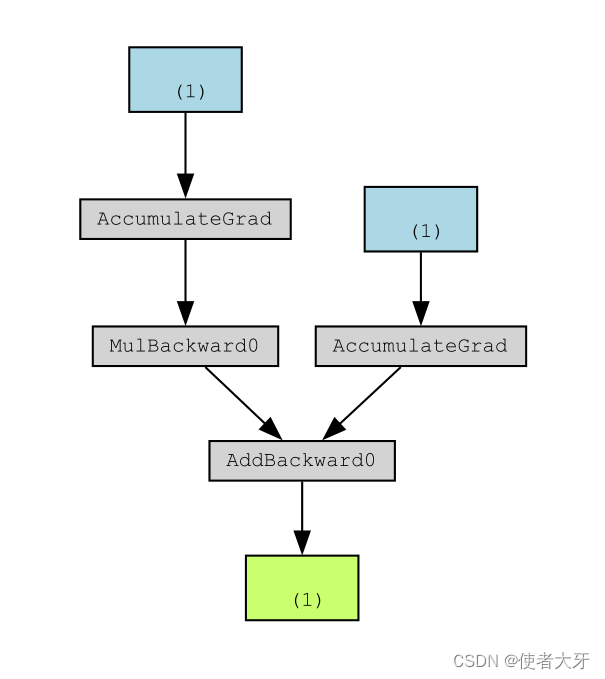
基于TorchViz详解计算图(附代码)
文章目录 0. 前言1. 计算图是什么?2. TorchViz的安装3. 计算图详解 0. 前言 按照国际惯例,首先声明:本文只是我自己学习的理解,虽然参考了他人的宝贵见解,但是内容可能存在不准确的地方。如果发现文中错误,…...

解决GitHub的速度很慢的几种方式
1. GitHub 镜像访问 这里提供两个最常用的镜像地址: https://hub.njuu.cf/search https://www.gitclone.com/gogs/search/clonesearch 也就是说上面的镜像就是一个克隆版的 GitHub,你可以访问上面的镜像网站,网站的内容跟 GitHub 是完整同步…...
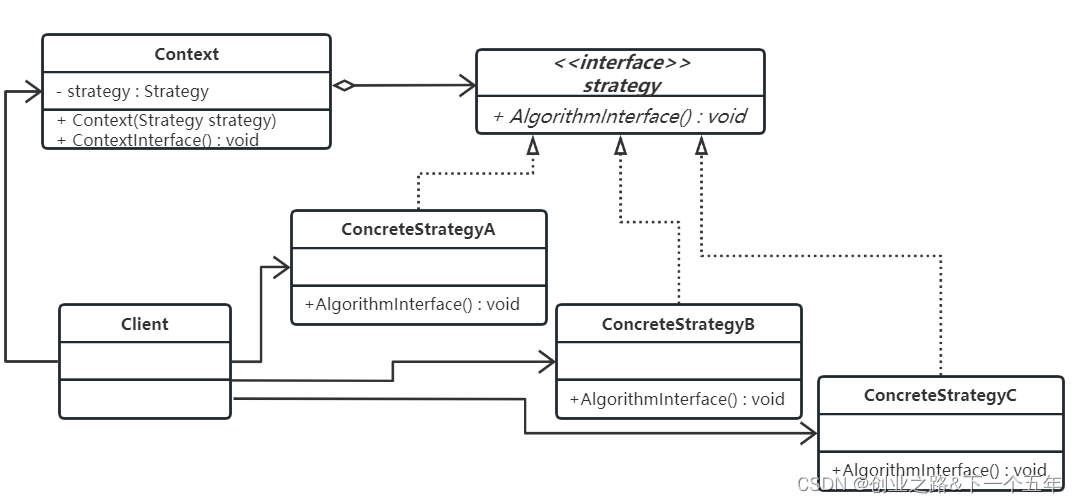
设计模式再探——策略模式
目录 一、背景介绍二、思路&方案三、过程1.策略模式简介2.策略模式的类图3.策略模式代码4.策略模式还可以优化的地方5.策略模式的例子改造(配置文件反射) 四、总结五、升华 一、背景介绍 最近在做产品的过程中,对于主题讨论回复内容,按照追评次数排…...
基于Googlenet深度学习网络的人员行为动作识别matlab仿真
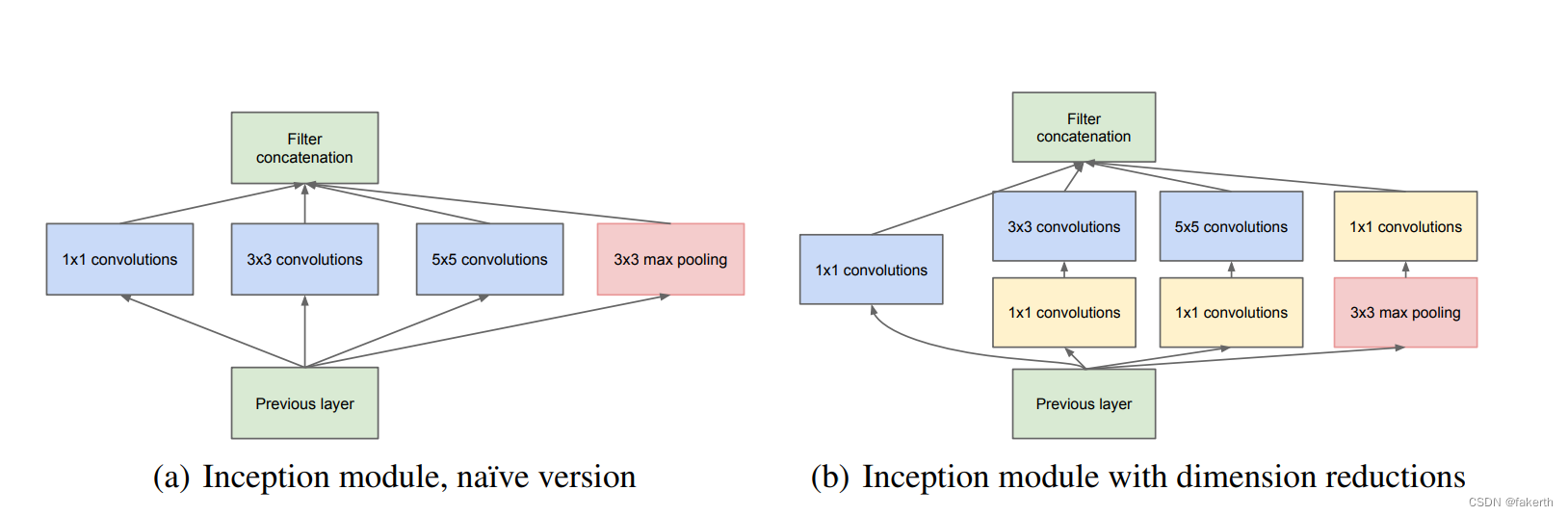
目录 1.算法运行效果图预览 2.算法运行软件版本 3.部分核心程序 4.算法理论概述 1. 原理 1.1 深度学习与卷积神经网络(CNN) 1.2 GoogLeNet 2. 实现过程 2.1 数据预处理 2.2 构建网络模型 2.3 数据输入与训练 2.4 模型评估与调优 3. 应用领域…...

存储过程的学习
1,前言 这是实习期间学习的,我可能是在学校没好好听课,(或者就是学校比较垃,没教这部分,在公司经理让我下去自己学习,太难了,因为是公司代码很多部分都是很多表的操作&#…...

zookeeperAPI操作与写数据原理
要执行API操作需要在idea中创建maven项目 (改成自己的阿里仓库)导入特定依赖 添加日志文件 上边操作做成后就可以进行一些API的实现了 目录 导入maven依赖: 创建日志文件: 创建API客户端: (1)…...

防火墙对双通道协议的处理
防火墙是一种网络安全设备或软件,用于控制网络流量并保护计算机网络免受未经授权的访问、恶意攻击和网络威胁。它作为网络的第一道防线,用于监视、过滤和管理进出网络的数据包。 防火墙可以基于预设的安全策略对网络流量进行评估和筛选。它通过比较数据…...
vscode搭建c语言环境问题
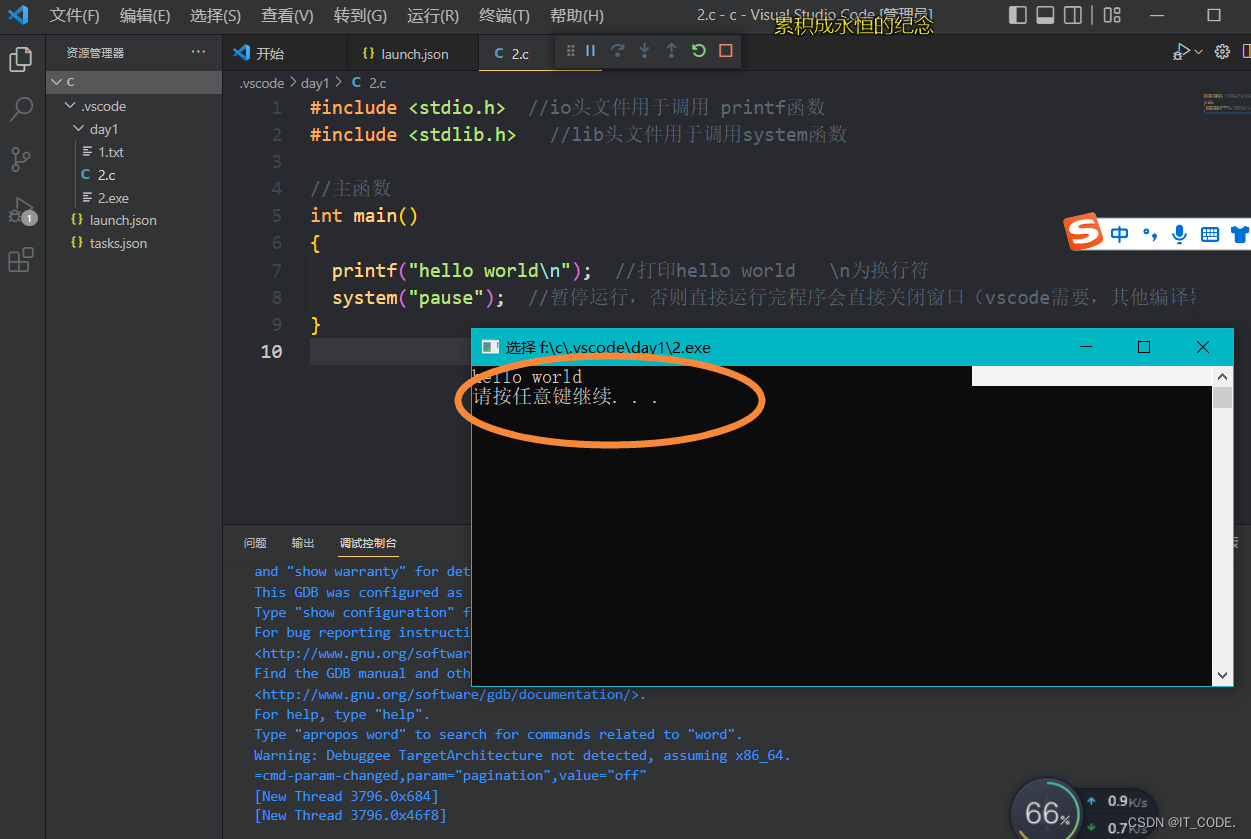
c语言环境搭建参考文章:【C语言初级阶段学习1】使用vscode运行C语言,vscode配置环境超详细过程(包括安装vscode和MinGW-W64安装及后续配置使用的详细过程,vscode用户代码片段的使用)[考研专用]_QAQshift的博客-CSDN博客 问题如下:…...
全网最全的接口自动化测试教程
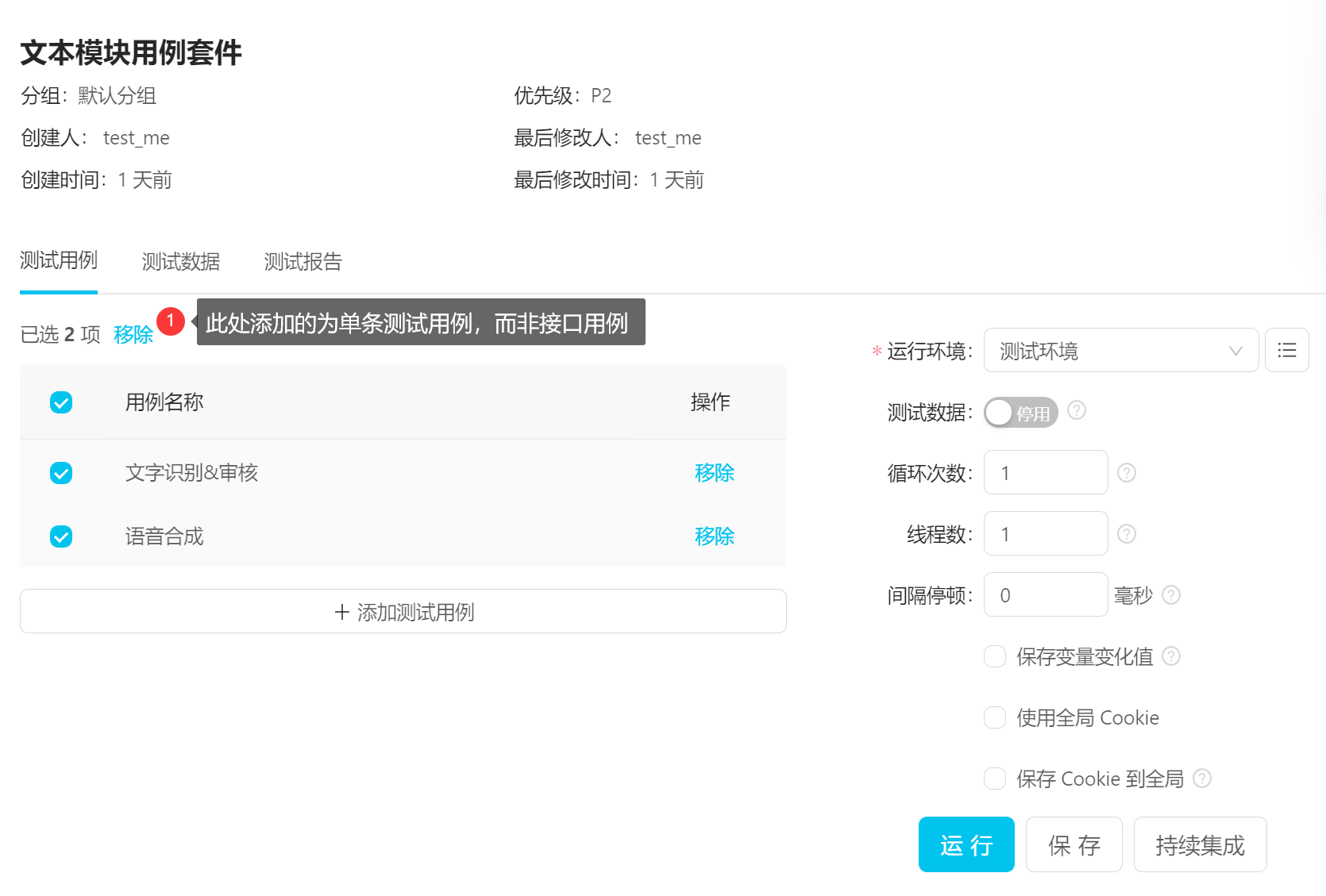
为什么要做接口自动化 相对于UI自动化而言,接口自动化具有更大的价值。 为了优化转化路径或者提升用户体验,APP/web界面的按钮控件和布局几乎每个版本都会发生一次变化,导致自动化的代码频繁变更,没有起到减少工作量的效果。 而…...
数据结构----结构--线性结构--链式存储--链表
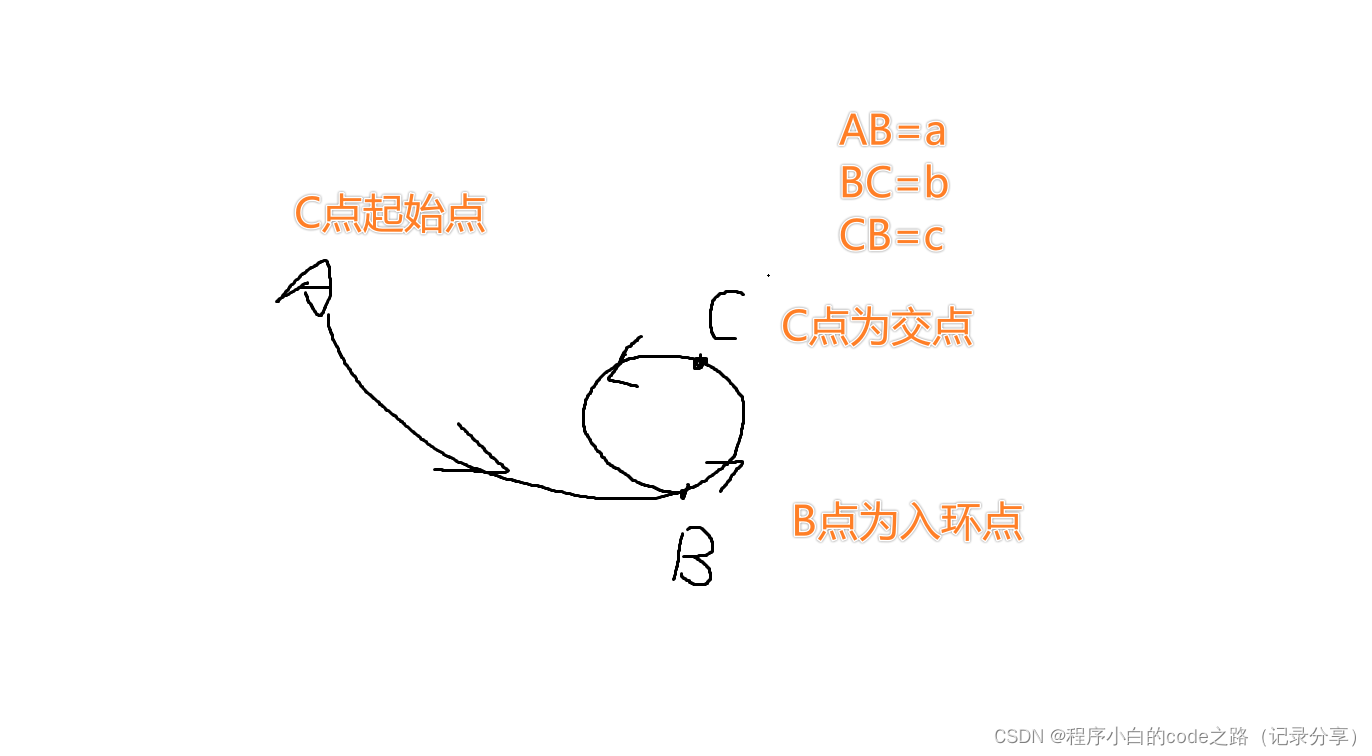
数据结构----结构–线性结构–链式存储–链表 1.链表的特点 空间可以不连续,长度不固定,相对于数组灵活自由 搜索: 时间复杂度O(n) 增删: 头增头删时间复杂度O(1) 其他时间复杂度为O(n) 扩展:单向循环链表的特性 从任意节…...

【5G 核心网】5G 多PDU会话锚点技术介绍
博主未授权任何人或组织机构转载博主任何原创文章,感谢各位对原创的支持! 博主链接 本人就职于国际知名终端厂商,负责modem芯片研发。 在5G早期负责终端数据业务层、核心网相关的开发工作,目前牵头6G算力网络技术标准研究。 博客…...
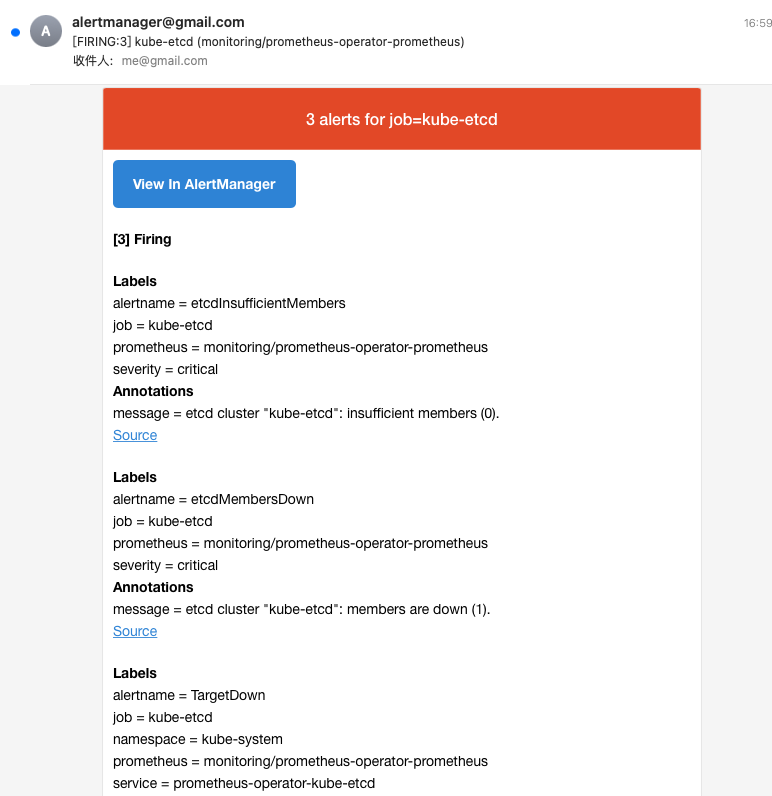
K8s环境下监控告警平台搭建及配置
Promethues是可以单机搭建的,参考prometheus入门[1] 本文是就PromethuesGrafana在K8s环境下的搭建及配置 Prometheus度量指标监控平台简介 启动minikube minikube start 安装helm 使用Helm Chart 安装 Prometheus Operator: helm install prometheus-operator stabl…...
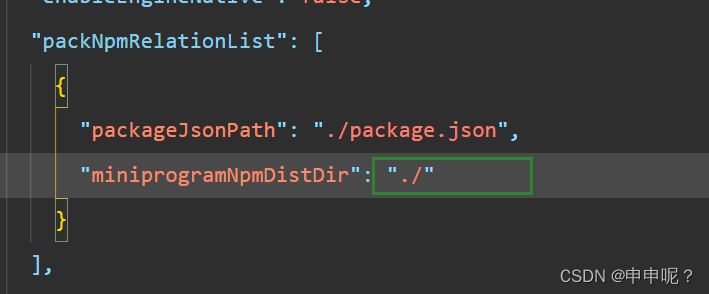
微信小程序在使用vant组件库时构建npm报错
在跟着vant官方进行使用步骤一步步操作时,由于要构建NPM,但NPM包在App配置文件的外部 所以在做下图这一步时: 接着再进行npm构建时会报错 message:发生错误 Error: F:\前端学习\前端框架\小程序\project\demo\miniprogram解决方法 …...
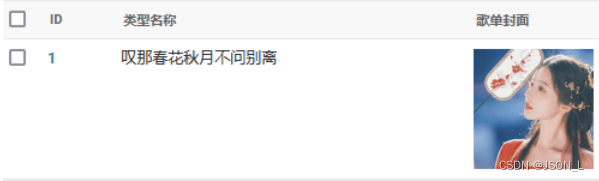
Django实现音乐网站 ⑽
使用Python Django框架制作一个音乐网站, 本篇主要是后台对歌曲类型、歌单功能原有功能进行部分功能实现和显示优化。 目录 歌曲类型功能优化 新增编辑 优化输入项标题显示 父类型显示改为下拉菜单 列表显示 父类型显示名称 过滤器增加父类型 歌单表功能优化…...

SpringMVC的架构有什么优势?——异常处理与文件上传(五)
前言 「作者主页」:雪碧有白泡泡 「个人网站」:雪碧的个人网站 「推荐专栏」: ★java一站式服务 ★ ★ React从入门到精通★ ★前端炫酷代码分享 ★ ★ 从0到英雄,vue成神之路★ ★ uniapp-从构建到提升★ ★ 从0到英雄ÿ…...

【java面向对象中static关键字】
提纲 static修饰成员变量static修饰成员变量的应用场景static修饰成员方法static修饰成员方法的应用场景static的注意事项static的应用知识:代码块static的应用知识:单例设计模式 static静态的意思,可以修饰成员变量,成员方法&a…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...
