【考研数学】概率论与梳理统计 | 第一章——随机事件与概率(1)
文章目录
- 一、随机试验与随机事件
- 1.1 随机试验
- 1.2 样本空间
- 1.3 随机事件
- 二、事件的运算与关系
- 2.1 事件的运算
- 2.2 事件的关系
- 2.3 事件运算的性质
- 三、概率的公理化定义与概率的基本性质
- 3.1 概率的公理化定义
- 3.2 概率的基本性质
- 写在最后
一、随机试验与随机事件
1.1 随机试验
若一个试验满足如下条件:
- 在相同的条件下该试验可重复进行;
- 试验的结果是多样的且所有可能的结果在试验前都是确定的;
- 某次试验之前不确定具体发生的结果,
这样的试验称为随机试验,简称试验,一般用字母 E E E 表示。
1.2 样本空间
设 E E E 为随机试验,随机试验 E E E 的所有可能的基本结果所组成的集合,称为随机试验 E E E 的样本空间,记为 Ω \Omega Ω , Ω \Omega Ω 中的任意一个元素称为样本点。
1,样本空间里面所有的元素必须是最基本的,即不可再分。
2,样本空间必须是所有可能的基本结果,即具有完备性,且同一个基本结果在样本空间中只出现一次。
1.3 随机事件
设 E E E 为随机试验, Ω \Omega Ω 为其样本空间,则 Ω \Omega Ω 的子集称为随机事件,其中 ∅ \emptyset ∅ 称为不可能事件, Ω \Omega Ω 称为必然事件。
二、事件的运算与关系
2.1 事件的运算
设 A , B A,B A,B 为两个随机事件,则事件 A A A 与事件 B B B 同时发生的事件,称为事件 A , B A,B A,B 的积事件,记为 A B AB AB 或 A ⋂ B A\bigcap B A⋂B ,如下图所示。

事件 A A A 或事件 B B B 发生的事件(即事件 A A A 与事件 B B B 至少有一个事件发生的事件),称为事件 A , B A,B A,B 的和事件,记为 A + B A+B A+B 或 A ⋃ B A\bigcup B A⋃B ,如下图所示。

事件 A A A 发生而事件 B B B 不发生的事件,称为事件 A , B A,B A,B 的差事件,记为 A − B A-B A−B 。事件 A A A 不发生的事件,称为事件 A A A 的补事件,记为 A ‾ \overline{A} A 。
2.2 事件的关系
设 A , B A,B A,B 为两个随机事件,若事件 A A A 发生时,事件 B B B 一定发生,则称 A A A 包含于 B B B ,记为 A ⊂ B A\subset B A⊂B 。若有 A ⊂ B , B ⊂ A A\subset B,B\subset A A⊂B,B⊂A ,称两事件相等,记为 A = B A=B A=B 。
若事件 A A A 与 B B B 不能同时发生,称事件 A , B A,B A,B 不相容或互斥,如下图所示。

若事件 A A A 与 B B B 不能同时发生,但至少会有一个发生,称事件 A , B A,B A,B 为对立事件,如下图所示。
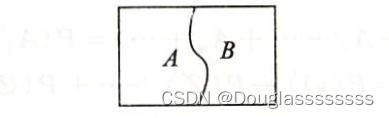
(1) A = ( A − B ) + A B A=(A-B)+AB A=(A−B)+AB ,且 A − B A-B A−B 与 A B AB AB 互斥。
(2) A + B = ( A − B ) + ( B − A ) + A B A+B=(A-B)+(B-A)+AB A+B=(A−B)+(B−A)+AB ,且 A − B , B − A , A B A-B,B-A,AB A−B,B−A,AB 两两互斥。
(3) A B ⊂ A ⊂ A + B , A B ⊂ B ⊂ A + B AB\subset A\subset A+B,AB\subset B\subset A+B AB⊂A⊂A+B,AB⊂B⊂A+B 。
(4)事件 A , B A,B A,B 互斥的充要条件是 A B = ∅ AB=\empty AB=∅ 。
(5)事件 A , B A,B A,B 对立的充要条件是 A B = ∅ AB=\empty AB=∅ ,且 A + B = Ω A+B=\Omega A+B=Ω 。
2.3 事件运算的性质
好多啊,如果要记住的话可费劲了,还容易错,最好还是结合图示来记忆和推吧。
1. A B = B A , A + B = B + A ; AB=BA,A+B=B+A; AB=BA,A+B=B+A;
2. ( 1 ) A ⋃ A = A , A ⋂ A = A ; (1)A\bigcup A=A,A\bigcap A=A; (1)A⋃A=A,A⋂A=A;
( 2 ) A ⋂ ( B ⋃ C ) = ( A ⋂ B ) ⋃ ( A ⋂ C ) , A ⋃ ( B ⋂ C ) = ( A ⋃ B ) ⋂ ( A ⋃ C ) ; (2)A\bigcap(B\bigcup C)=(A\bigcap B)\bigcup (A\bigcap C),A \bigcup (B \bigcap C)=(A\bigcup B) \bigcap (A \bigcup C); (2)A⋂(B⋃C)=(A⋂B)⋃(A⋂C),A⋃(B⋂C)=(A⋃B)⋂(A⋃C);
3.(1) A = ( A − B ) ⋃ A ; A=(A-B) \bigcup A; A=(A−B)⋃A;
( 2 ) ( A − B ) ⋂ A = A − B ; (2)(A-B)\bigcap A=A-B; (2)(A−B)⋂A=A−B;
( 3 ) A + B = ( A − B ) ⋃ A B ⋃ ( B − A ) ; (3)A+B=(A-B)\bigcup AB \bigcup (B-A); (3)A+B=(A−B)⋃AB⋃(B−A);
4.(1) A + A ‾ = Ω ; A+\overline{A}=\Omega; A+A=Ω;
( 2 ) A ⋂ A ‾ = ∅ ; (2)A \bigcap \overline{A} =\empty; (2)A⋂A=∅;
5.(1) A ∩ B ‾ = A ‾ ∪ B ‾ ; \overline{A\cap B}=\overline{A}\cup \overline{B}; A∩B=A∪B;
( 2 ) A ‾ ∩ B ‾ = A ∪ B ‾ (2)\overline{A}\cap\overline{B}=\overline{A\cup B} (2)A∩B=A∪B
第 5 条的结论比较有规律,很像戴帽子和脱帽子,都要变运算。同样有如下运算性质: A ∪ B ‾ = A ‾ ∩ B ‾ , A ‾ ∪ B ‾ = A ∩ B ‾ \overline{A\cup B}=\overline{A}\cap \overline{B},\overline{A}\cup\overline{B}=\overline{A\cap B} A∪B=A∩B,A∪B=A∩B
三、概率的公理化定义与概率的基本性质
3.1 概率的公理化定义
设随机试验 E E E 的样本空间为 Ω \Omega Ω ,在 Ω \Omega Ω 上定义满足如下条件的随机事件的函数 P ( A ) ( A ⊂ Ω ) P(A)(A \subset \Omega) P(A)(A⊂Ω) ,称为事件 A A A 的概率:
(1)(非负性) 对任意的事件 A A A ,有 P ( A ) ≥ 0 ; P(A) \geq 0; P(A)≥0;
(2)(归一性) P ( Ω ) = 1 ; P(\Omega)=1; P(Ω)=1;
(3)(可列可加性) 设 A 1 , A 2 , … , A n , … A_1,A_2,\dots,A_n,\dots A1,A2,…,An,… 为不相容的随机事件,则有 P ( ⋃ n = 1 ∞ A n ) = ∑ n = 1 ∞ P ( A n ) , P(\bigcup_{n=1}^{\infty}A_n)=\sum_{n=1}^{\infty}P(A_n), P(n=1⋃∞An)=n=1∑∞P(An), 则对任意的 A ⊂ Ω A\subset \Omega A⊂Ω ,称 P ( A ) P(A) P(A) 为事件 A A A 的概率。
3.2 概率的基本性质
(一) P ( ∅ ) = 0. P(\empty)=0. P(∅)=0.
证明:令 A 1 = A 2 = ⋯ = A n = ⋯ = ∅ A_1=A_2= \dots=A_n=\dots=\empty A1=A2=⋯=An=⋯=∅ ,有 A 1 = A 2 = ⋯ = A n = … A_1=A_2= \dots=A_n=\dots A1=A2=⋯=An=… 互不相容,由可列可加性,有 P ( A 1 + A 2 + ⋯ + A n + … ) = P ( A 1 ) + P ( A 2 ) + … P ( A n ) + … , P(A_1+A_2+ \dots+A_n+\dots)=P(A_1)+P(A_2)+\dots P(A_n)+\dots, P(A1+A2+⋯+An+…)=P(A1)+P(A2)+…P(An)+…, 由 A 1 + A 2 + ⋯ + A n + ⋯ = ∅ A_1+A_2+ \dots+A_n+\dots =\empty A1+A2+⋯+An+⋯=∅ ,可得 P ( ∅ ) = P ( ∅ ) + P ( ∅ ) + ⋯ + P ( ∅ ) + … , P(\empty)=P(\empty)+P(\empty)+\dots+P(\empty)+\dots , P(∅)=P(∅)+P(∅)+⋯+P(∅)+…, 故 P ( ∅ ) = 0 P(\empty)=0 P(∅)=0 。
(二)(有限可加性) 设 A 1 , A 2 , … , A n A_1,A_2,\dots,A_n A1,A2,…,An 为互斥的有限个随机事件列,则 P ( ⋃ k = 1 n A k ) = ∑ k = 1 n P ( A k ) . P(\bigcup_{k=1}^{n}A_k)=\sum_{k=1}^{n}P(A_k). P(k=1⋃nAk)=k=1∑nP(Ak). 证明:取 A n + 1 = A n + 2 = ⋯ = ∅ A_{n+1}=A_{n+2}=\dots=\empty An+1=An+2=⋯=∅ ,则 A 1 , A 2 , … , A n , … A_1,A_2,\dots,A_n,\dots A1,A2,…,An,… 为不相容的随机事件,由 P ( A n + 1 ) = P ( A n + 2 ) = ⋯ = 0 P(A_{n+1})=P(A_{n+2})=\dots=0 P(An+1)=P(An+2)=⋯=0 及可列可加性,可得 P ( ⋃ n = 1 ∞ A n ) = P ( ⋃ k = 1 n A k ) = P ( A 1 ) + P ( A 2 ) + … P ( A n ) = ∑ k = 1 n P ( A k ) . P(\bigcup_{n=1}^{\infty}A_n)=P(\bigcup_{k=1}^{n}A_k)=P(A_1)+P(A_2)+\dots P(A_n)=\sum_{k=1}^{n}P(A_k). P(n=1⋃∞An)=P(k=1⋃nAk)=P(A1)+P(A2)+…P(An)=k=1∑nP(Ak). (三)(补概率的公式) : P ( A ‾ ) = 1 − P ( A ) . P(\overline{A})=1-P(A). P(A)=1−P(A).
写在最后
剩下关于概率的基本公式、独立事件以及贝叶斯和概型,放到下一篇文章吧。
相关文章:

【考研数学】概率论与梳理统计 | 第一章——随机事件与概率(1)
文章目录 一、随机试验与随机事件1.1 随机试验1.2 样本空间1.3 随机事件 二、事件的运算与关系2.1 事件的运算2.2 事件的关系2.3 事件运算的性质 三、概率的公理化定义与概率的基本性质3.1 概率的公理化定义3.2 概率的基本性质 写在最后 一、随机试验与随机事件 1.1 随机试验 …...
LeetCode 36题:有效的数独
题目 请你判断一个 9 x 9 的数独是否有效。只需要 根据以下规则 ,验证已经填入的数字是否有效即可。 数字 1-9 在每一行只能出现一次。数字 1-9 在每一列只能出现一次。数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。(请参考示例图ÿ…...
word横向页面侧面页码设置及转pdf后横线变竖线的解决方案
在处理材料的时候,会遇到同一个文档里自某一页开始,页面布局是横向的,这时候页码要设置在侧面,方法是双击页脚,然后在word工具栏上选择“插入”——>“文本框”——>“绘制竖版文本框”,然后在页面左…...
)
华为OD机试 - 字符串划分(Java JS Python)
题目描述 给定一个小写字母组成的字符串 s,请找出字符串中两个不同位置的字符作为分割点,使得字符串分成三个连续子串且子串权重相等,注意子串不包含分割点。 若能找到满足条件的两个分割点,请输出这两个分割点在字符串中的位置下标,若不能找到满足条件的分割点请返回0,…...
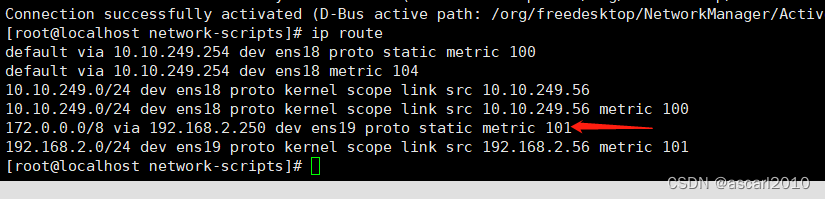
使用 `nmcli` 在 CentOS 8 上添加永久路由
CentOS 8 使用 NetworkManager 作为默认的网络管理工具,因此我们可以使用 nmcli 工具来实现相同的目标。使用 nmcli 可以更加直观地管理路由,并且更符合 CentOS 8 的默认网络管理方式。 以下是使用 nmcli 在 CentOS 8 上添加永久路由的步骤:…...

Java基础五之for循环小练习
加油,新时代大工人! 一、Java基础之算术运算符 二、Java基础之类型转换 三、Java基础之【字符串操作以及自增自减操作】 四、Java基础之赋值运算符和关系运算符 package base;import java.io.InputStream; import java.util.Scanner;/*** author wh* date 2023年08…...

解决 Python RabbitMQ/Pika 报错:pop from an empty deque
使用 python 的 pika 包连接rabbitmq,代码如下: import pika import threading import timedef on_message(channel, method_frame, header_frame, body):print(fon_message thread id: {threading.get_ident()})delivery_tag method_frame.delivery_t…...
观察者模式实战
场景 假设创建订单后需要发短信、发邮件等其它的操作,放在业务逻辑会使代码非常臃肿,可以使用观察者模式优化代码 代码实现 自定义一个事件 发送邮件 发送短信 最后再创建订单的业务逻辑进行监听,创建订单 假设后面还需要做其它的…...
035_小驰私房菜_Qualcomm账号注册以及提case流程
全网最具价值的Android Camera开发学习系列资料~ 作者:8年Android Camera开发,从Camera app一直做到Hal和驱动~ 欢迎订阅,相信能扩展你的知识面,提升个人能力~ 一、账号注册 1)登陆高通网站Wireless Technology & Innovation | Mobile Technology | Qualcomm, 采用…...
uniapp input输入框placeholder文本右对齐
input输入框placeholder文本右对齐 给input标签加上placeholder-class,这个是给placeholder设置样式,右对齐这就是text-align:right;字体颜色之类依次编辑即可。...

分布式监控平台—zabbix
前言一、zabbix概述1.1 什么是zabbix1.2 zabbix的监控原理1.3 zabbix常见五个应用程序1.4 zabbix的监控模式1.5 监控架构1.5.1 C/S(server—client)1.5.2 server—proxy—client1.5.3 master—node—client 二、部署zabbix2.1 部署 zabbix server 端2.2 …...

【leetcode】第一章数组-2
977. 有序数组的平方 简单的方法是平方后使用排序方法第2种方法是双指针方法,从两边进行判断,将最大的从后往前放 public static int[] sortedSquares(int[] nums) {// 输入:nums [-4,-1,0,3,10]// 输出:[0,1,9,16,100]// 解释…...

程序使用Microsoft.XMLHTTP对象请求https时出错解决
程序中使用Microsoft.XMLHTTP组件请求https时出现如下错误: 出错程序代码示例: strUrl "https://www.xxx.com/xxx.asp?id11" dim objXmlHttp set objXmlHttp Server.CreateObject("Microsoft.XMLHTTP") objXmlHttp.open "…...

Linux安装配置nginx+php搭建
Linux安装配置nginxphp搭建 文章目录 Linux安装配置nginxphp搭建1.nginx源码包编译环境和安装相应的依赖1.1 安装编译环境1.2 安装pcre库、zlib库和openssl库 2.安装nginx2.1 在[nginx官网](https://nginx.org/en/download.html)上获取源码包并进行下载2.2 进行解压编译 3.启动…...

springboot的各种配置
1.AOP配置 <!-- AOP的依赖 --><dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-aop</artifactId></dependency>package com.qf.HomeWork.aop;import lombok.extern.slf4j.Slf4j; im…...
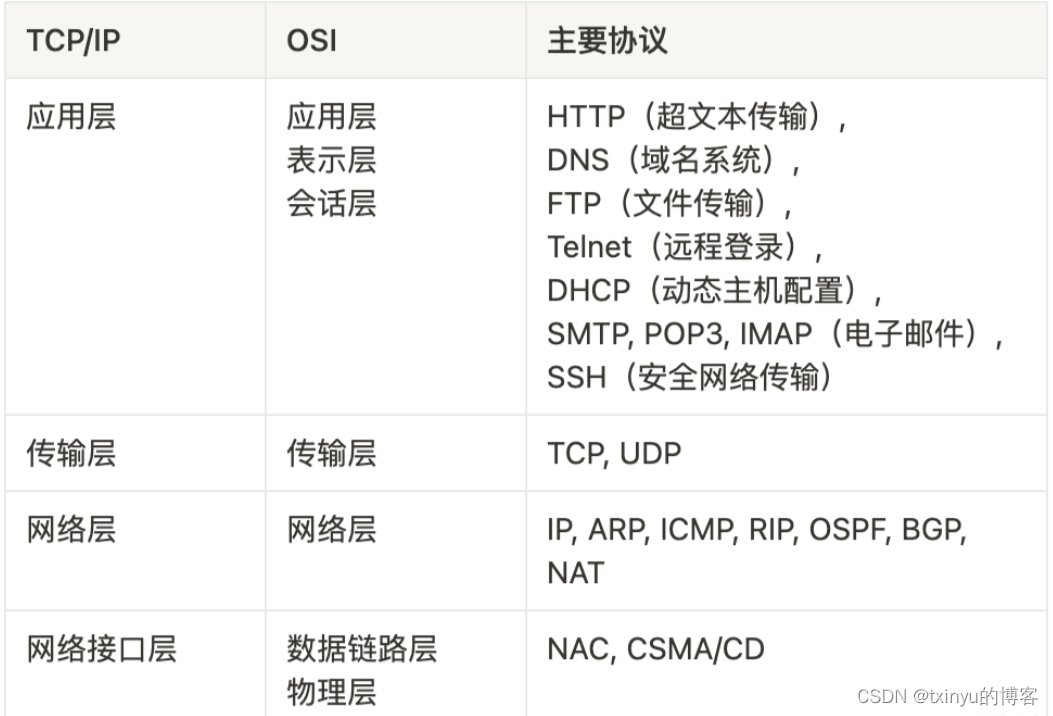
OSI七层模型及TCP/IP四层模型
目录 OSI七层模型 TCP/IP四层模型 OIS七层模型和TCP/IP模型图 七层详解 两种模型比较 为什么OSI七层体系结构不常用 四层详解 网络为什么要分层? 说说 OSI 七层模型和 TCP/IP 四层模型的关系和区别 OSI七层模型 OSI(Open System Interconnect&a…...

MDN-Web APIs
参考资料 文章目录 简介DOM APIXMLHttpRequestWeb Storage APIWebsockets API 简介 Web APIs(Application Programming Interfaces)是用于与浏览器环境中的 Web 功能进行交互的一组接口和方法集合。通过 Web APIs,开发人员可以访问浏览器提…...

2023国赛数学建模C题思路分析
文章目录 0 赛题思路1 竞赛信息2 竞赛时间3 建模常见问题类型3.1 分类问题3.2 优化问题3.3 预测问题3.4 评价问题 4 建模资料 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 竞赛信息 全国大学生数学建模…...

暑假集训笔记
刷题刷的好累啊...不想刷题了...然后就来写题解了... 昨天晚上打了场div2..2000来名,加了155分....现在rating1281...我是菜鸡..暑假之前就打到了1200分以上了,结果暑假一掉再掉,直接掉到1100了...然后我就一直压力很大....... 昨天在机房打…...

【枚举+推式子】牛客小白月赛 63 E
登录—专业IT笔试面试备考平台_牛客网 题意: 思路: 首先是个计数问题,考虑组合数学 组合数学就是在考虑枚举所有包含1和n的区间 这个典中典就是枚举1和n的位置然后算贡献 双指针超时,考虑推式子: Code:…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案
目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后,迭代器会失效,因为顺序迭代器在内存中是连续存储的,元素删除后,后续元素会前移。 但一些场景中,我们又需要在执行删除操作…...

FFmpeg avformat_open_input函数分析
函数内部的总体流程如下: avformat_open_input 精简后的代码如下: int avformat_open_input(AVFormatContext **ps, const char *filename,ff_const59 AVInputFormat *fmt, AVDictionary **options) {AVFormatContext *s *ps;int i, ret 0;AVDictio…...

恶补电源:1.电桥
一、元器件的选择 搜索并选择电桥,再multisim中选择FWB,就有各种型号的电桥: 电桥是用来干嘛的呢? 它是一个由四个二极管搭成的“桥梁”形状的电路,用来把交流电(AC)变成直流电(DC)。…...
