DIP: Spectral Bias of DIP 频谱偏置解释DIP

On Measuring and Controlling the Spectral Bias of the Deep Image Prior
文章目录
- On Measuring and Controlling the Spectral Bias of the Deep Image Prior
- 1. 方法原理
- 1.1 动机
- 1.2 相关概念
- 1.3 方法原理
- 频带一致度量与网络退化
- 谱偏移和网络结构的关系
- Lipschitz-controlled 卷积层
- Gaussian-controlled 上采样层
- 自动停止迭代过程
- 2. 实验结果
- 3. 总结
文章地址:https://arxiv.org/pdf/2107.01125.pdf
代码地址: https://github.com/shizenglin/Measure-and-Control-Spectral-Bias
参考博客: https://zhuanlan.zhihu.com/p/598650125
1. 方法原理
1.1 动机
动机
- Deep Image Prior已经被广泛地应用于去噪、超分、图像恢复等
- 但是我们尚不清楚如何在网络架构的选择之外控制DIP
- DIP存在性能达到峰值之后退化的问题 --> 需要early stopping
贡献
- 使用谱偏移度量和解释 DIP的原理
- DIP学习目标图像低频分量的效率比高频分量高
- 控制谱偏移
- 使用Lipschitz-controlled 正则化和 Lipschitz 批归一化加速和稳定优化过程
- 使用 上采样方法(bilinear upsampling)引入了倾向于恢复低频分量的特点(谱偏移)
- 使用了一种简单的early stopping策略防止多余的计算
1.2 相关概念
谱偏移原则是指:神经网络拟合低频信息的效率比高频信息快
相关文章参考:
- On the Spectral Bias of Neural Networks
- FREQUENCY PRINCIPLE: FOURIER ANALYSIS SHEDS LIGHT ON DEEP NEURAL NETWORKS
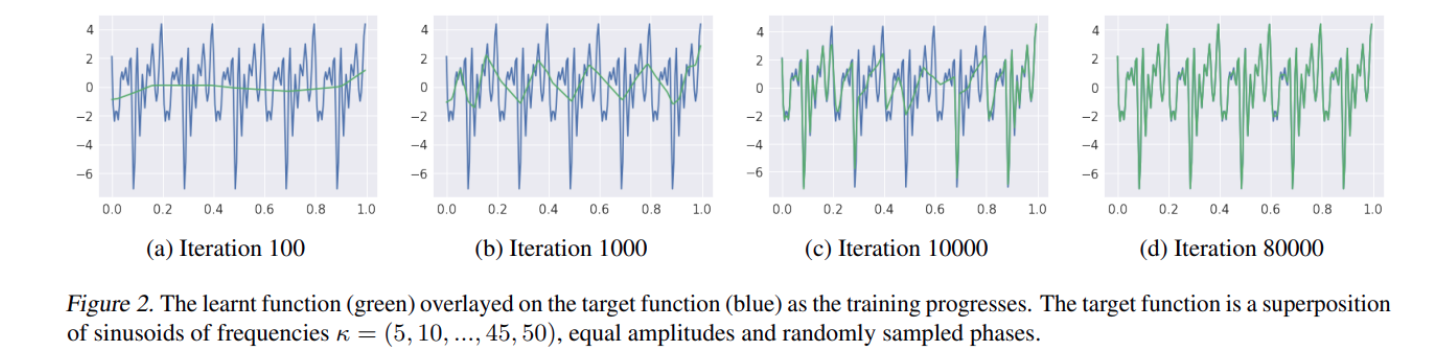
用其中的一些图进行解释:
- 随着迭代的进行,神经网络的输出(绿色线)首先拟合的是真实观测数据的低频,然后再去逐渐拟合高频
反(逆)问题:根据观测结果获取真实模型的一种求解模式。具体的可以参考
- Untrained Neural Network Priors for Inverse Imaging Problems: A Survey
注意反问题求解存在一个普遍的问题:多解性。也就是多个反演结果的合成数据都可以和观测数据匹配。通常一个减少多解性的方法就是添加约束条件(在公式中表现为正则化约束)
1.3 方法原理
频带一致度量与网络退化
这篇文章是从频率域的角度进行谱偏移分析的,用 { θ 1 , . . . , θ T } \{\theta^{1},...,\theta^{T}\} {θ1,...,θT}表示第对应迭代次数网络的参数,用 { f θ 1 , . . . , f θ T } \{f_{\theta^{1}},...,f_{\theta^{T}}\} {fθ1,...,fθT}表示对应的网格过程。对图片频率分析需要使用傅里叶变换获得 频率域的信息,用 F ( f θ ( t ) ) F(f_{\theta^{(t)}}) F(fθ(t))表示。频谱图的表示如下:

如果对标签图片也做一次傅里叶变换,那么可以求解网络输出和这个结果的比值
H θ ( t ) = F { f θ ( t ) } F { y 0 } H_{\theta^{(t)}} = \frac{F\{f_{\theta^{(t)}}\}}{F\{y_0\}} Hθ(t)=F{y0}F{fθ(t)}
- 这个比值越接近于1表示网络输出和标签的相关性越高
- H图像是一个以中心对称的图像,这里为方便统计就将其分割成为多个同心圆环,求圆环中的平均值作为这个圈内的值。也就是将一个二维的度量变为了一个一维的度量。
- 文章中将频率划分为了:lowest、low、medium、high和highest五个部分

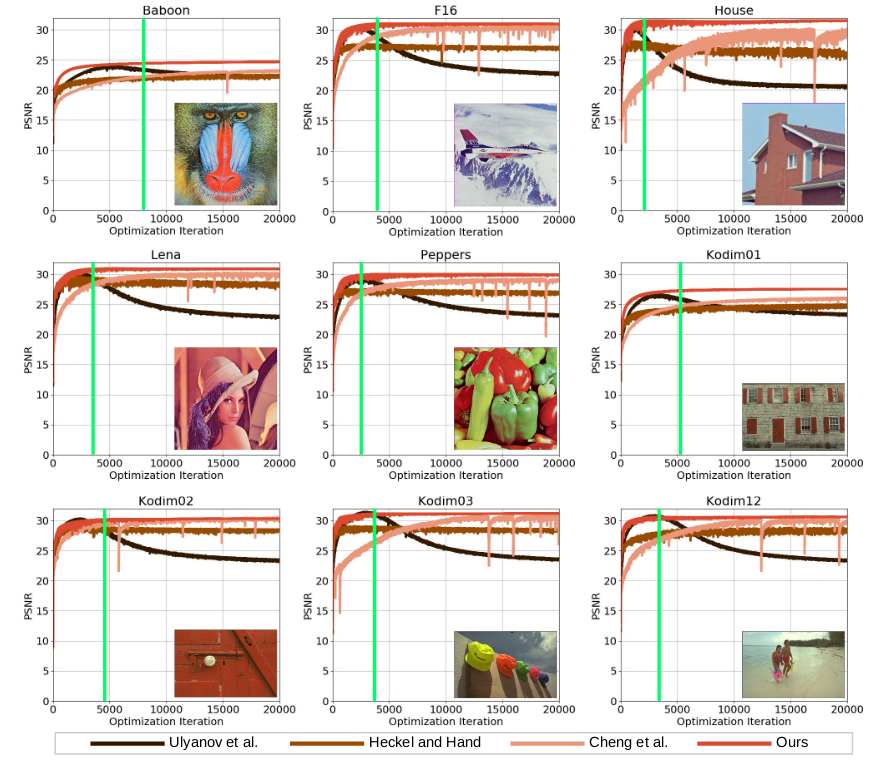
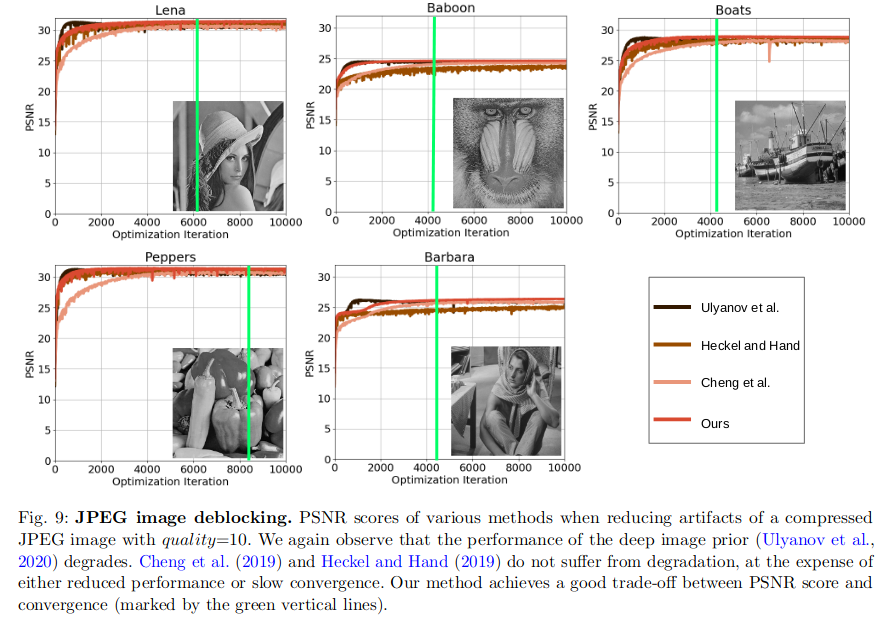
这个度量比值在DIP不同应用场景中随着迭代次数的变化
- 随着DIP迭代次数的增加,PSNR会先达到最高然后缓慢降低(性能达到峰值之后会下降)
- 在PSRN最高的时候(图中绿线),恰好是lowest分量的频带一致性刚好最高的时候
- 通过下图验证了 DIP也存在谱偏移的现象:低频分量学得更快且频带一致性很高,而高频分量学习相对较慢且频带一致性较低
- 随着高频部分的频带一致性提高,PSNR下降
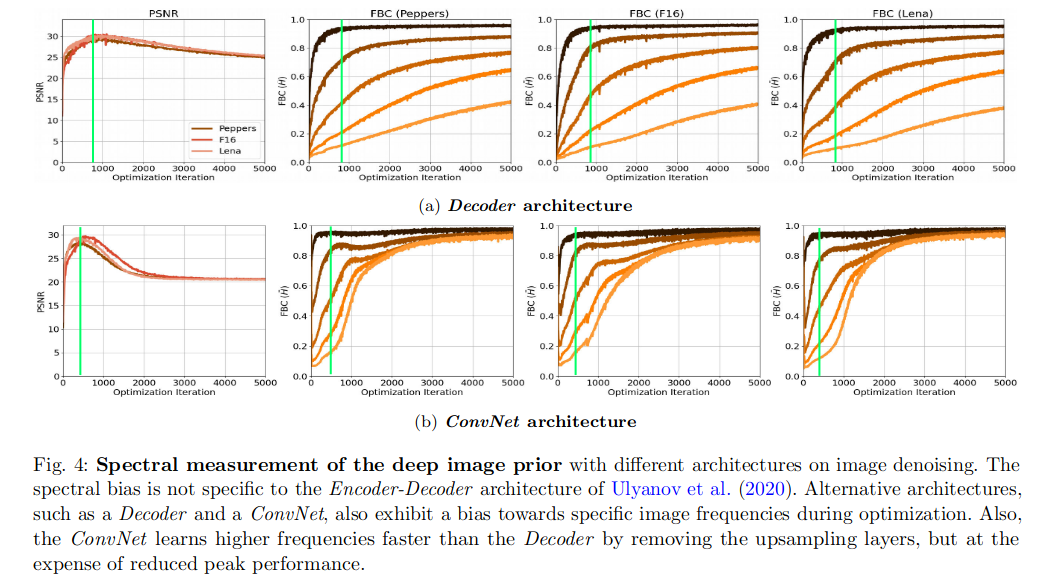
谱偏移和网络结构的关系
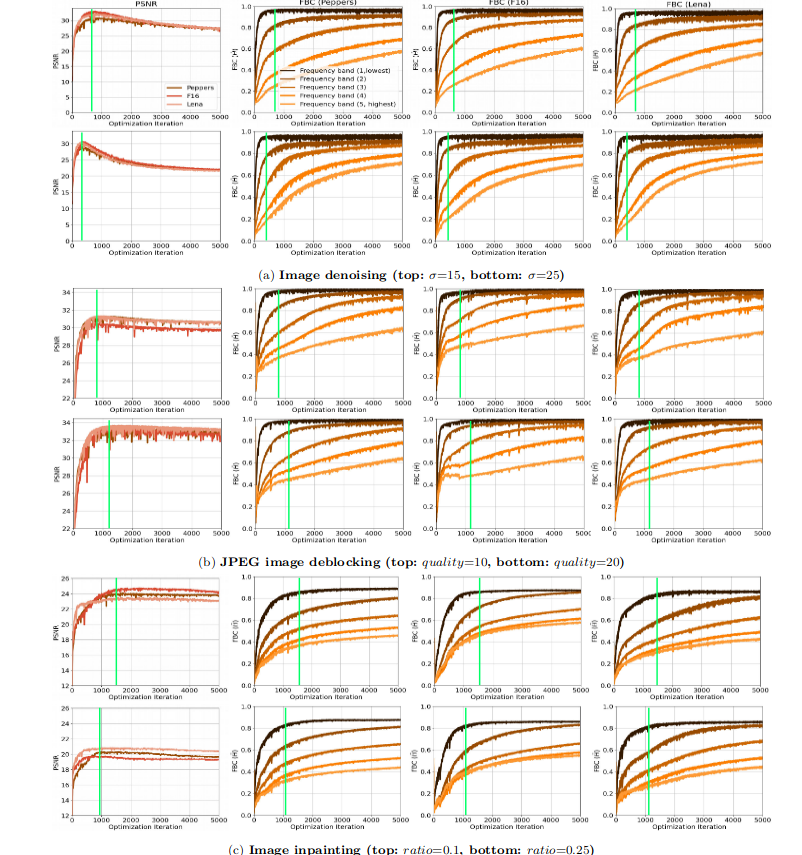
前面有研究表示Encoder-Decoder结构的DIP效果更好,这里作者对比了三种不同结构进行测试对比(a. 没有Encoder部分的DIP; b. 没有上采样层的DIP;):
- 不论什么结构谱偏移都存在
- 去掉上采样层的Decoder结构(ConvNet)拟合高频的效率更高,这里表现为高频部分的频带一致性高
- 无上采样层的ConvNet结构最大的PSNR比Decoder和DIP低
结论
- 无训练网络UNNP可以解决逆图像问题的原因是:低频学习效率高,高频学习效率相对较慢(谱偏移)
- 高频信息通常为为结构高频信息和噪声高频信息,当网络开始学习噪声高频信息的时候,网络恢复的性能开始下降
- 这里通过一个类似消融实验的方法说明上采样层是可以提高PSNR的,但是这会影响低频的收敛速度
防止网络退化,平衡性能与效率的方向
- 保证性能的前提下,使用参数量更少的 Decoder结构 替代DIP的 Encoder-Decoder结构
- 性能退化:抑制网络对高频噪声的学习(使用上采样层)
- 加速收敛:使用更合适的上采样层
- 提前停止策略:自动检测?
Lipschitz-controlled 卷积层
从频率域理解卷积操作
- 对一个时间域/空间域的变量做一个傅里叶变换其实是将作用域变换到了频率域,这样的其中一个作用是:
- 将空间域的卷积操作 变为 频率域的乘积操作,简化计算
- 当然对于信号处理还有更多的好处,比如FK变换可以用于滤波
- 图像和“卷积核”的作用在频率域其实就是一个乘积过程
卷积核具有滤波的作用,但是什么样的卷积核可以抑制高频呢?
L-Lipschitz连续
这个概念很有意思,WGAN-GP中也用到了
其定义是:如果函数f在区间Q中,以常数L Lipschitz连续,那么对于 x , y ∈ Q x,y \in Q x,y∈Q有:
∣ ∣ f ( x ) − f ( y ) ∣ ∣ ≤ L ∣ ∣ x − y ∣ ∣ ||f(x)- f(y)|| \leq L||x - y|| ∣∣f(x)−f(y)∣∣≤L∣∣x−y∣∣
常数L就被称为函数f在区间Q上的 Lipschitz常数。Lipschitz连续其实是限制了连续函数f的局部变动幅度不能超过某一个常量。我个人感觉一个非常更简单地理解这个概念的方法就是将稍微变动一下这个公式:
∣ ∣ f ( x ) − f ( y ) ∣ ∣ ∣ ∣ x − y ∣ ∣ ≤ L \frac{||f(x)- f(y)||}{||x - y||} \leq L ∣∣x−y∣∣∣∣f(x)−f(y)∣∣≤L
这个东西看起来就像是求导了,更多的可以参考https://blog.csdn.net/FrankieHello/article/details/105739610

结合Lipschitz和频谱分析
假设卷积层的 f f f是符合C-Lipschitz的,存在:
∣ f ^ ( k ) ∣ ≤ C ∣ k ∣ 2 ≤ ∣ ∣ w ∣ ∣ s n ∣ k ∣ 2 |\hat{f}(k)| \leq \frac{C}{|k|^2} \leq \frac{||w||_{sn}}{|k|^2} ∣f^(k)∣≤∣k∣2C≤∣k∣2∣∣w∣∣sn
- k表示频率, ∣ f ^ ( k ) ∣ |\hat{f}(k)| ∣f^(k)∣表示傅里叶系数的模(有实部和虚部)
- 分母是 k 2 k^2 k2表示在高频的时候衰减很强,学习更高的频率需要更高的频谱范数(分子)
- ∣ ∣ w ∣ ∣ s n ||w||_{sn} ∣∣w∣∣sn 表示卷积层参数矩阵w的谱范数,可以通过限制谱范数的上限来限制卷积层学习更高频率的能力
- ∣ ∣ w ∣ ∣ w ∣ ∣ s n ∣ ∣ s n = 1 ||\frac{w}{||w||_{sn}}||_{sn} = 1 ∣∣∣∣w∣∣snw∣∣sn=1, ∣ ∣ w λ ∣ ∣ w ∣ ∣ s n ∣ ∣ s n = λ ||\frac{w\lambda}{||w||_{sn}}||_{sn} = \lambda ∣∣∣∣w∣∣snwλ∣∣sn=λ
- w m a x ( 1 , ∣ ∣ w ∣ ∣ s n / λ ) \frac{w}{max(1,||w||_{sn}/\lambda)} max(1,∣∣w∣∣sn/λ)w
注意这里我们想要达到的一个效果就是:限制最高可以学习的频率。可以选择一个合适的 λ \lambda λ在保证恢复效果的同时不去恢复噪声信号。
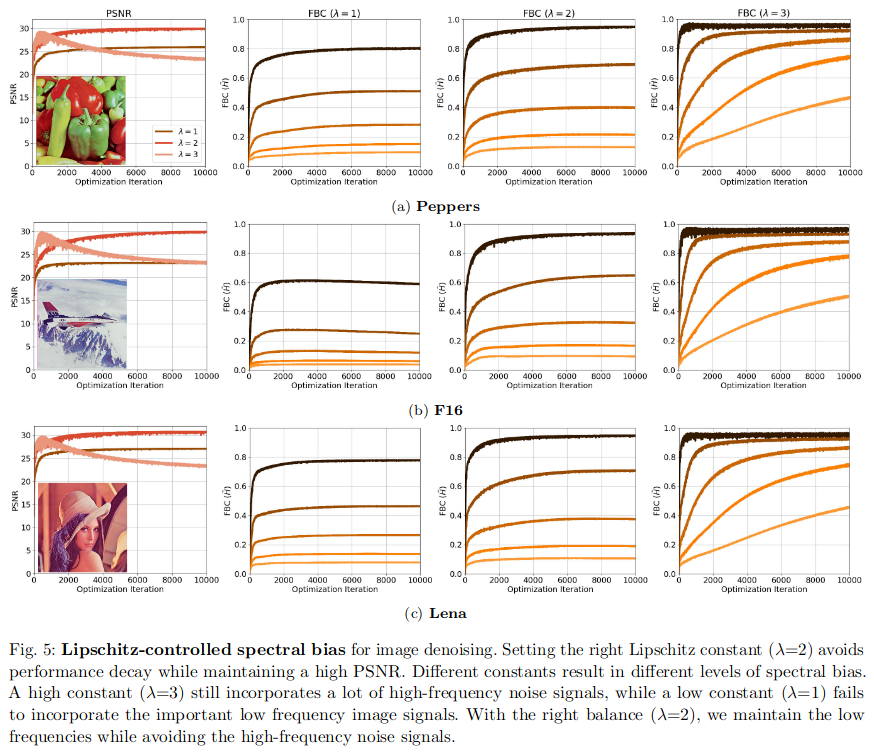
其他网络层对Lipschitz常数的影响

Gaussian-controlled 上采样层
插值、邻近上采样层的平滑操作会让DIP网络收敛速度变慢,但是上采样层对于抑制高频信息又有一定的作用,为了平衡二者作者引入了 gaussian-controlled上采样层。
方法就是:转置卷积 + 高斯核
- 转置卷积可以自定义上采样的卷积核

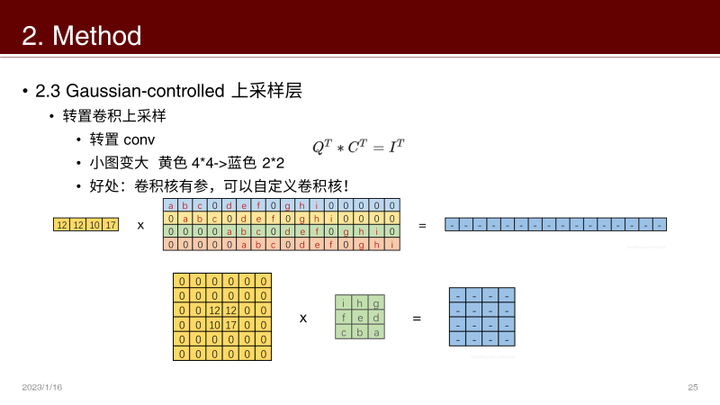
- 为了控制平滑程度,卷积核最简单的就是高斯核

- 实验不同的高斯核: σ \sigma σ越小收敛越快,但是PSNR越小

自动停止迭代过程
- 利用Lipschitz方法限制了网络学习的最高频率噪声,避免了网络的退化
- 当高频部分到达了上界限,也就意味着网络在之前就已经收敛了
- 怎么评估高频到达了上界限
- r = B l u r r i n e s s S h a r p n e s s r = \frac{Blurriness}{Sharpness} r=SharpnessBlurriness
- 即当模糊度/锐度之间的导数小于预先设置的阈值的时候,停止迭代
- r ( f θ ) = B ( f θ ) / S ( f θ ) r(f_{\theta}) = B(f_{\theta})/S(f_{\theta}) r(fθ)=B(fθ)/S(fθ)
- Δ r ( f θ ( t ) ) = ∣ 1 n ∑ i = 1 n r ( f θ ( t − n − i ) ) − 1 n ∑ i = 1 n r ( f θ ( t − n − i ) ) ∣ \Delta r(f_{\theta ^{(t)}}) = |\frac{1}{n}\sum_{i=1}^{n}r(f_{\theta}^{(t-n-i)}) - \frac{1}{n}\sum_{i=1}^{n}r(f_{\theta}^{(t-n-i)})| Δr(fθ(t))=∣n1i=1∑nr(fθ(t−n−i))−n1i=1∑nr(fθ(t−n−i))∣
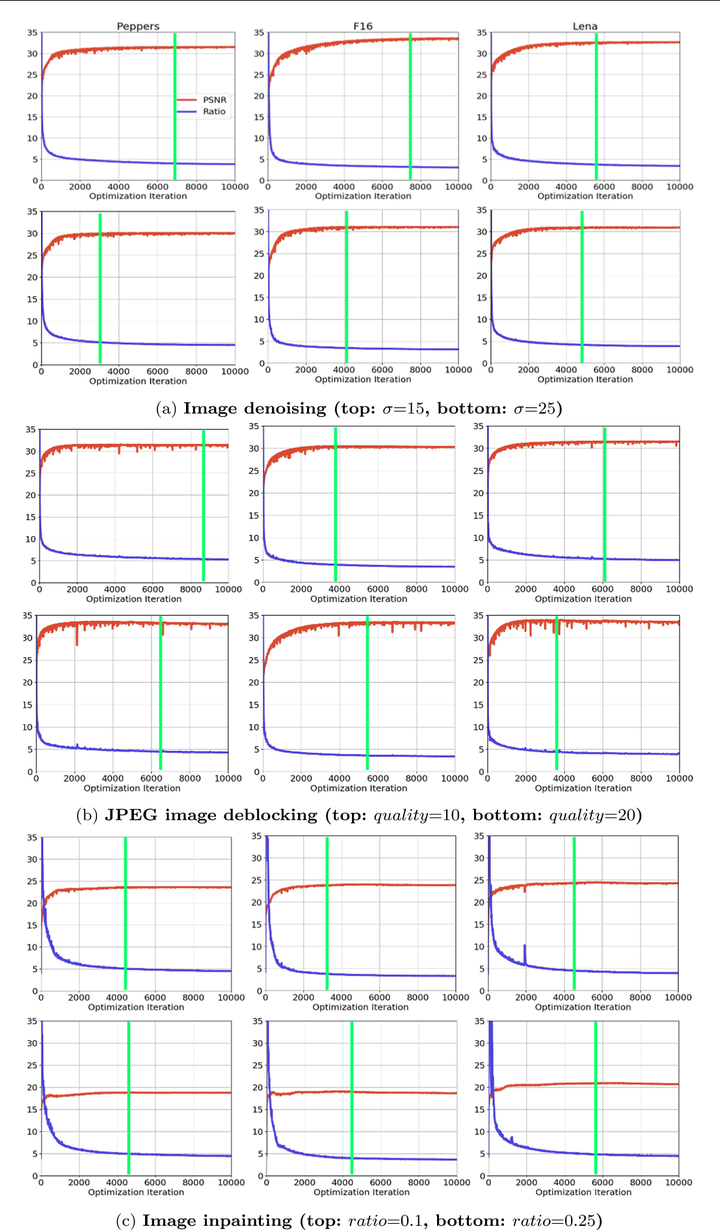
2. 实验结果
-
去噪
-
-
Image deblockign
-
Image Inpainting
-
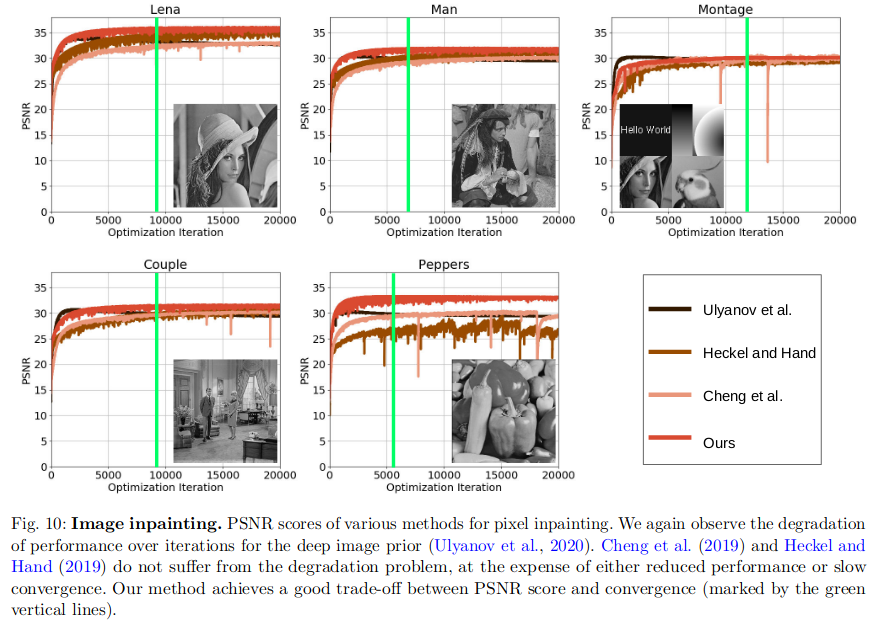
3. 总结
研究思路
- 从谱偏置方向分析DIP的工作,网络先拟合低频信息,逐渐拟合高频信息
- 怎么控制拟合高频信息?–> 高频截断 --> 应用Lipschitz理论控制,解决网络层退化的问题
- 网络训练慢怎么解决?–>分析发现常规的上采样层相当于一个低通滤波器,引入了过多的低频分量导致很多时候收敛非常慢,所以使用 gaussian 核控制的转置卷积方法 平衡网络收敛效率的问题。
- 怎么Early stopping 减少迭代次数? --> 使用模糊度与锐度的比值的导数进行衡量
优点
- 将GAN 谱优化的策略放到DIP之中,在频率域中分析各个层的性质:低频收敛快,高频收敛慢。
- 用谱偏置的思路解释了网络退化问题
- 提出频带一致性、模糊度和锐度比值梯度 平衡了DIP收敛效率和效果
改进方向
- 就个人观点:噪声这里假设都是高频的,但是低频噪声、结构噪声是否会有影响?
- 该研究给实际应用DIP提供了很大的可能性,但是就实验效果来看并没有提升,甚至有所下降。所以基于这种方法怎么去同时提高效果?
- 就我个人想法:继续减少参数化网络的参数量(PIP等工作),并且提高恢复的效果(持续研究方向) 是现在的研究方向。
相关文章:

DIP: Spectral Bias of DIP 频谱偏置解释DIP
On Measuring and Controlling the Spectral Bias of the Deep Image Prior 文章目录 On Measuring and Controlling the Spectral Bias of the Deep Image Prior1. 方法原理1.1 动机1.2 相关概念1.3 方法原理频带一致度量与网络退化谱偏移和网络结构的关系Lipschitz-controlle…...
【考研数学】概率论与梳理统计 | 第一章——随机事件与概率(1)
文章目录 一、随机试验与随机事件1.1 随机试验1.2 样本空间1.3 随机事件 二、事件的运算与关系2.1 事件的运算2.2 事件的关系2.3 事件运算的性质 三、概率的公理化定义与概率的基本性质3.1 概率的公理化定义3.2 概率的基本性质 写在最后 一、随机试验与随机事件 1.1 随机试验 …...
LeetCode 36题:有效的数独
题目 请你判断一个 9 x 9 的数独是否有效。只需要 根据以下规则 ,验证已经填入的数字是否有效即可。 数字 1-9 在每一行只能出现一次。数字 1-9 在每一列只能出现一次。数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。(请参考示例图ÿ…...
word横向页面侧面页码设置及转pdf后横线变竖线的解决方案
在处理材料的时候,会遇到同一个文档里自某一页开始,页面布局是横向的,这时候页码要设置在侧面,方法是双击页脚,然后在word工具栏上选择“插入”——>“文本框”——>“绘制竖版文本框”,然后在页面左…...
)
华为OD机试 - 字符串划分(Java JS Python)
题目描述 给定一个小写字母组成的字符串 s,请找出字符串中两个不同位置的字符作为分割点,使得字符串分成三个连续子串且子串权重相等,注意子串不包含分割点。 若能找到满足条件的两个分割点,请输出这两个分割点在字符串中的位置下标,若不能找到满足条件的分割点请返回0,…...
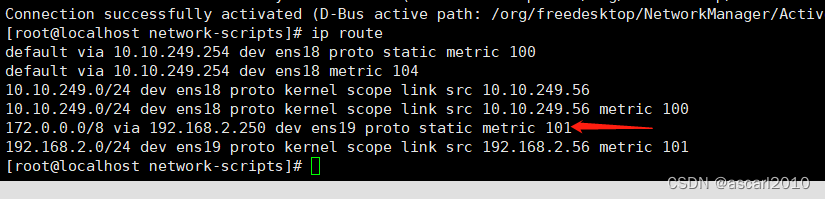
使用 `nmcli` 在 CentOS 8 上添加永久路由
CentOS 8 使用 NetworkManager 作为默认的网络管理工具,因此我们可以使用 nmcli 工具来实现相同的目标。使用 nmcli 可以更加直观地管理路由,并且更符合 CentOS 8 的默认网络管理方式。 以下是使用 nmcli 在 CentOS 8 上添加永久路由的步骤:…...

Java基础五之for循环小练习
加油,新时代大工人! 一、Java基础之算术运算符 二、Java基础之类型转换 三、Java基础之【字符串操作以及自增自减操作】 四、Java基础之赋值运算符和关系运算符 package base;import java.io.InputStream; import java.util.Scanner;/*** author wh* date 2023年08…...

解决 Python RabbitMQ/Pika 报错:pop from an empty deque
使用 python 的 pika 包连接rabbitmq,代码如下: import pika import threading import timedef on_message(channel, method_frame, header_frame, body):print(fon_message thread id: {threading.get_ident()})delivery_tag method_frame.delivery_t…...
观察者模式实战
场景 假设创建订单后需要发短信、发邮件等其它的操作,放在业务逻辑会使代码非常臃肿,可以使用观察者模式优化代码 代码实现 自定义一个事件 发送邮件 发送短信 最后再创建订单的业务逻辑进行监听,创建订单 假设后面还需要做其它的…...
035_小驰私房菜_Qualcomm账号注册以及提case流程
全网最具价值的Android Camera开发学习系列资料~ 作者:8年Android Camera开发,从Camera app一直做到Hal和驱动~ 欢迎订阅,相信能扩展你的知识面,提升个人能力~ 一、账号注册 1)登陆高通网站Wireless Technology & Innovation | Mobile Technology | Qualcomm, 采用…...
uniapp input输入框placeholder文本右对齐
input输入框placeholder文本右对齐 给input标签加上placeholder-class,这个是给placeholder设置样式,右对齐这就是text-align:right;字体颜色之类依次编辑即可。...

分布式监控平台—zabbix
前言一、zabbix概述1.1 什么是zabbix1.2 zabbix的监控原理1.3 zabbix常见五个应用程序1.4 zabbix的监控模式1.5 监控架构1.5.1 C/S(server—client)1.5.2 server—proxy—client1.5.3 master—node—client 二、部署zabbix2.1 部署 zabbix server 端2.2 …...

【leetcode】第一章数组-2
977. 有序数组的平方 简单的方法是平方后使用排序方法第2种方法是双指针方法,从两边进行判断,将最大的从后往前放 public static int[] sortedSquares(int[] nums) {// 输入:nums [-4,-1,0,3,10]// 输出:[0,1,9,16,100]// 解释…...

程序使用Microsoft.XMLHTTP对象请求https时出错解决
程序中使用Microsoft.XMLHTTP组件请求https时出现如下错误: 出错程序代码示例: strUrl "https://www.xxx.com/xxx.asp?id11" dim objXmlHttp set objXmlHttp Server.CreateObject("Microsoft.XMLHTTP") objXmlHttp.open "…...

Linux安装配置nginx+php搭建
Linux安装配置nginxphp搭建 文章目录 Linux安装配置nginxphp搭建1.nginx源码包编译环境和安装相应的依赖1.1 安装编译环境1.2 安装pcre库、zlib库和openssl库 2.安装nginx2.1 在[nginx官网](https://nginx.org/en/download.html)上获取源码包并进行下载2.2 进行解压编译 3.启动…...

springboot的各种配置
1.AOP配置 <!-- AOP的依赖 --><dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-aop</artifactId></dependency>package com.qf.HomeWork.aop;import lombok.extern.slf4j.Slf4j; im…...
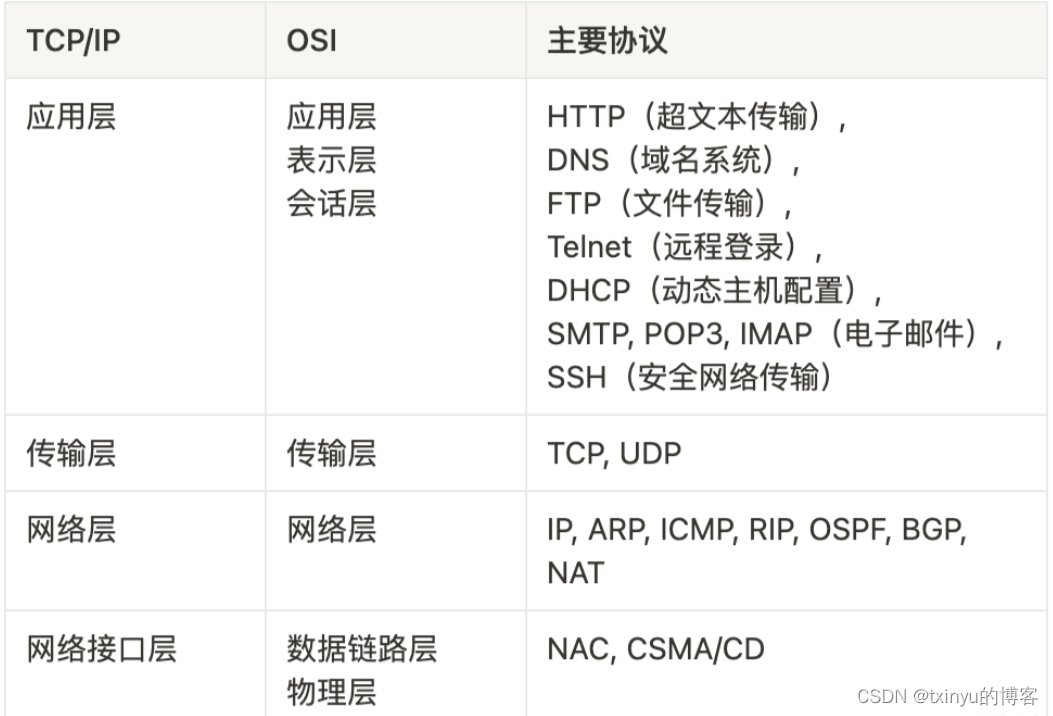
OSI七层模型及TCP/IP四层模型
目录 OSI七层模型 TCP/IP四层模型 OIS七层模型和TCP/IP模型图 七层详解 两种模型比较 为什么OSI七层体系结构不常用 四层详解 网络为什么要分层? 说说 OSI 七层模型和 TCP/IP 四层模型的关系和区别 OSI七层模型 OSI(Open System Interconnect&a…...

MDN-Web APIs
参考资料 文章目录 简介DOM APIXMLHttpRequestWeb Storage APIWebsockets API 简介 Web APIs(Application Programming Interfaces)是用于与浏览器环境中的 Web 功能进行交互的一组接口和方法集合。通过 Web APIs,开发人员可以访问浏览器提…...

2023国赛数学建模C题思路分析
文章目录 0 赛题思路1 竞赛信息2 竞赛时间3 建模常见问题类型3.1 分类问题3.2 优化问题3.3 预测问题3.4 评价问题 4 建模资料 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 竞赛信息 全国大学生数学建模…...

暑假集训笔记
刷题刷的好累啊...不想刷题了...然后就来写题解了... 昨天晚上打了场div2..2000来名,加了155分....现在rating1281...我是菜鸡..暑假之前就打到了1200分以上了,结果暑假一掉再掉,直接掉到1100了...然后我就一直压力很大....... 昨天在机房打…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...

rknn toolkit2搭建和推理
安装Miniconda Miniconda - Anaconda Miniconda 选择一个 新的 版本 ,不用和RKNN的python版本保持一致 使用 ./xxx.sh进行安装 下面配置一下载源 # 清华大学源(最常用) conda config --add channels https://mirrors.tuna.tsinghua.edu.cn…...

node.js的初步学习
那什么是node.js呢? 和JavaScript又是什么关系呢? node.js 提供了 JavaScript的运行环境。当JavaScript作为后端开发语言来说, 需要在node.js的环境上进行当JavaScript作为前端开发语言来说,需要在浏览器的环境上进行 Node.js 可…...