Python-OpenCV中的图像处理-傅里叶变换
Python-OpenCV中的图像处理-傅里叶变换
- 傅里叶变换
- Numpy中的傅里叶变换
- Numpy中的傅里叶逆变换
- OpenCV中的傅里叶变换
- OpenCV中的傅里叶逆变换
- DFT的性能优化
- 不同滤波算子傅里叶变换对比
傅里叶变换
- 傅里叶变换经常被用来分析不同滤波器的频率特性。我们可以使用 2D 离散傅里叶变换 (DFT) 分析图像的频域特性。实现 DFT 的一个快速算法被称为快速傅里叶变换( FFT)。
- 对于一个正弦信号:x (t) = A sin (2πft), 它的频率为 f,如果把这个信号转到它的频域表示,我们会在频率 f 中看到一个峰值。如果我们的信号是由采样产生的离散信号组成,我们会得到类似的频谱图,只不过前面是连续的,现在是离散。你可以把图像想象成沿着两个方向采集的信号。所以对图像同时进行 X 方向和 Y 方向的傅里叶变换,我们就会得到这幅图像的频域表示(频谱图)。
- 对于一个正弦信号,如果它的幅度变化非常快,我们可以说他是高频信号,如果变化非常慢,我们称之为低频信号。你可以把这种想法应用到图像中,图像那里的幅度变化非常大呢?边界点或者噪声。所以我们说边界和噪声是图像中的高频分量(注意这里的高频是指变化非常快,而非出现的次数多)。如果没有如此大的幅度变化我们称之为低频分量。
Numpy中的傅里叶变换
Numpy 中的 FFT 包可以帮助我们实现快速傅里叶变换。函数 np.fft.fft2() 可以对信号进行频率转换,输出结果是一个复杂的数组。本函数的第一个参数是输入图像,要求是灰度格式。第二个参数是可选的, 决定输出数组的大小。输出数组的大小和输入图像大小一样。如果输出结果比输入图像大,输入图像就需要在进行 FFT 前补0。如果输出结果比输入图像小的话,输入图像就会被切割。
f = np.fft.fft2(img)
现在我们得到了结果,频率为 0 的部分(直流分量)在输出图像的左上角。如果想让它(直流分量)在输出图像的中心,我们还需要将结果沿两个方向平移 N/2 。函数 np.fft.fftshift() 可以帮助我们实现这一步。(这样更容易分析)。进行完频率变换之后,我们就可以构建振幅谱了。
fshift = np.fft.fftshift(f)
import numpy as np
import cv2
from matplotlib import pyplot as pltimg = cv2.imread('./resource/opencv/image/messi5.jpg', cv2.IMREAD_GRAYSCALE)
f = np.fft.fft2(img)
fshift = np.fft.fftshift(f)# 构建振幅图
magnitude_spectrum = 20*np.log(np.abs(fshift))plt.subplot(121), plt.imshow(img, cmap='gray'), plt.title('Input Image')
plt.subplot(122), plt.imshow(magnitude_spectrum, cmap='gray'), plt.title('Magnitude Spectrum')
plt.show()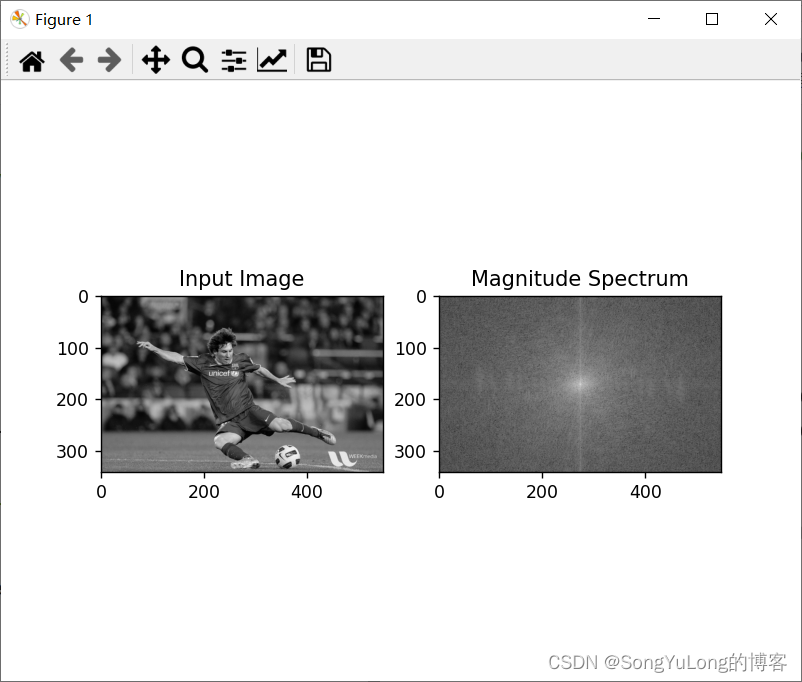
我们可以看到输出结果的中心部分更白(亮),这说明低频分量更多。
Numpy中的傅里叶逆变换
- 对图像进行FFT变换之后得到频域图像数据,然后再做IFFT变换又可以得到原始图像。相关函数:np.fft.ifftshift(),np.fft.ifft2()
fishift = np.fft.ifftshift(fshift)
img_ifft = np.fft.ifft2(fishift) - 我们可以对频域图像数据进行操作以实现一些图像处理效果,如在频域内将低频分量的值设为0,可以实现对图像的高通滤波处理:
rows, cols = img.shape
crow, ccol = int(rows/2) , int(cols/2)
fshift[crow-30:crow+30, ccol-30:ccol+30] = 0
import numpy as np
import cv2
from matplotlib import pyplot as pltimg = cv2.imread('./resource/opencv/image/messi5.jpg', cv2.IMREAD_GRAYSCALE)# 1.在Numpy内对图像进行傅里叶变换,得到其频域图像
f = np.fft.fft2(img)
fshift = np.fft.fftshift(f)
# 这里是构建振幅图,显示图像频谱
magnitude_spectrum = 20*np.log(np.abs(fshift))# 2.IFFT 将频域图像还原成原始图像,这里只是验证FFT的逆运算
fishift = np.fft.ifftshift(fshift)
img_ifft = np.fft.ifft2(fishift)
img_ifft = np.abs(img_ifft) # 取绝对值,否则不能用imshow()来显示图像# 3.在频域内将低频分量的值设为0,实现高通滤波。
rows, cols = img.shape
crow, ccol = int(rows/2) , int(cols/2)
fshift[crow-30:crow+30, ccol-30:ccol+30] = 0 # 4.对高通滤波后的图像频域数据进行逆傅里叶变换,得到高通滤波后图像。
f_ishift = np.fft.ifftshift(fshift)
img_back = np.fft.ifft2(f_ishift)
img_back = np.abs(img_back) # 取绝对值,否则不能用imshow()来显示图像
# 构建高通滤波后的振幅图,显示图像频谱
after_sepctrum = 20*np.log(np.abs(fshift))plt.subplot(231), plt.imshow(img, cmap='gray'), plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(232), plt.imshow(magnitude_spectrum, cmap='gray'), plt.title('Input Image Spectrum'), plt.xticks([]), plt.yticks([])
plt.subplot(233), plt.imshow(img_ifft, cmap='gray'), plt.title('Input IFFT'), plt.xticks([]), plt.yticks([])
plt.subplot(234), plt.imshow(after_sepctrum, cmap='gray'), plt.title('After HPF Spectrum'), plt.xticks([]), plt.yticks([])
plt.subplot(235), plt.imshow(img_back, cmap='gray'), plt.title('Image after HPF'), plt.xticks([]), plt.yticks([])
plt.subplot(236), plt.imshow(img_back), plt.title('Result in JET'), plt.xticks([]), plt.yticks([])
plt.show()
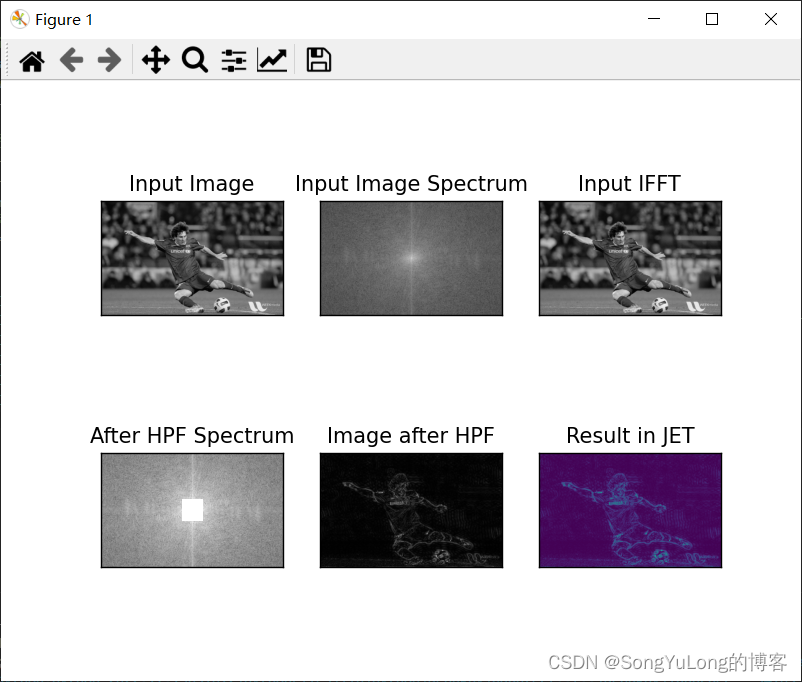
OpenCV中的傅里叶变换
OpenCV 中相应的函数是 cv2.dft() 和 cv2.idft()。和前面输出的结果一样,但是是双通道的。第一个通道是结果的实数部分,第二个通道是结果的虚数部分。输入图像要首先转换成 np.float32 格式。
import numpy as np
import cv2
from matplotlib import pyplot as pltimg = cv2.imread('./resource/opencv/image/messi5.jpg', cv2.IMREAD_GRAYSCALE)dft = cv2.dft(np.float32(img), flags=cv2.DFT_COMPLEX_OUTPUT)
dft_shift = np.fft.fftshift(dft)magnitude_spectrum = 20*np.log(cv2.magnitude(dft_shift[:,:,0], dft_shift[:,:,1]))plt.subplot(121), plt.imshow(img, cmap='gray'), plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122), plt.imshow(magnitude_spectrum, cmap='gray'), plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([])
plt.show()
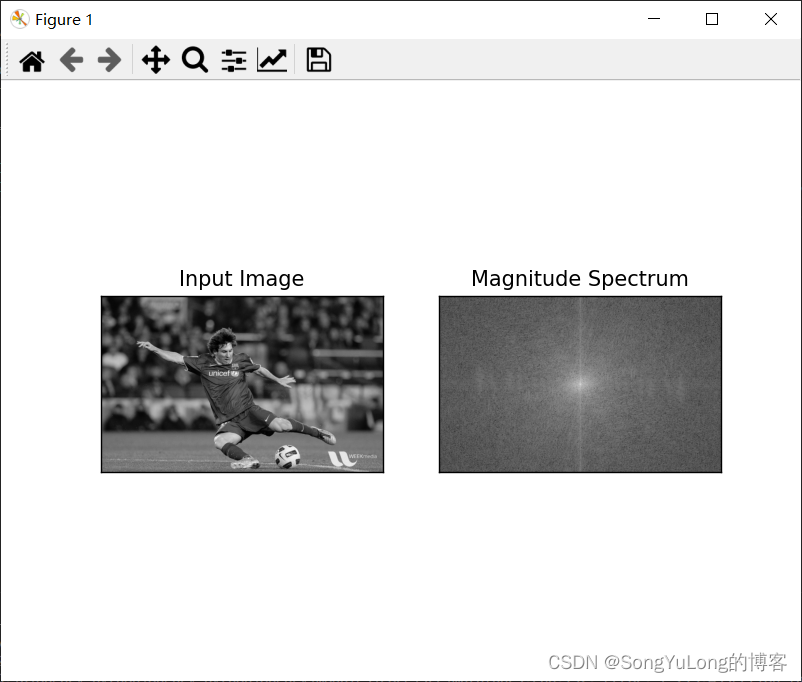
OpenCV中的傅里叶逆变换
前面的部分我们实现了一个 HPF(高通滤波)高通滤波其实是一种边界检测操作。现在我们来做 LPF(低通滤波)将高频部分去除。其实就是对图像进行模糊操作。首先我们需要构建一个掩模,与低频区域对应的地方设置为 1, 与高频区域对应的地方设置为 0。
import numpy as np
import cv2
from matplotlib import pyplot as pltimg = cv2.imread('./resource/opencv/image/messi5.jpg', cv2.IMREAD_GRAYSCALE)
# 1.OpenCV中做DFT
dft = cv2.dft(np.float32(img), flags=cv2.DFT_COMPLEX_OUTPUT)
dft_shift = np.fft.fftshift(dft)rows, cols = img.shape
crow, ccol = int(rows/2), int(cols/2)# create a mask first, center square is 1, remaining all zeros
mask = np.zeros((rows, cols, 2), np.uint8)
mask[crow-30:crow+30, ccol-30:ccol+30] = 1# apply mask and inverse DFT
fshift = dft_shift*mask
f_ishift = np.fft.ifftshift(fshift)
img_back = cv2.idft(f_ishift)
img_back = cv2.magnitude(img_back[:,:,0], img_back[:,:,1])plt.subplot(121), plt.imshow(img, cmap='gray'), plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122), plt.imshow(img_back, cmap='gray'), plt.title('Output Image'), plt.xticks([]), plt.yticks([])
plt.show()
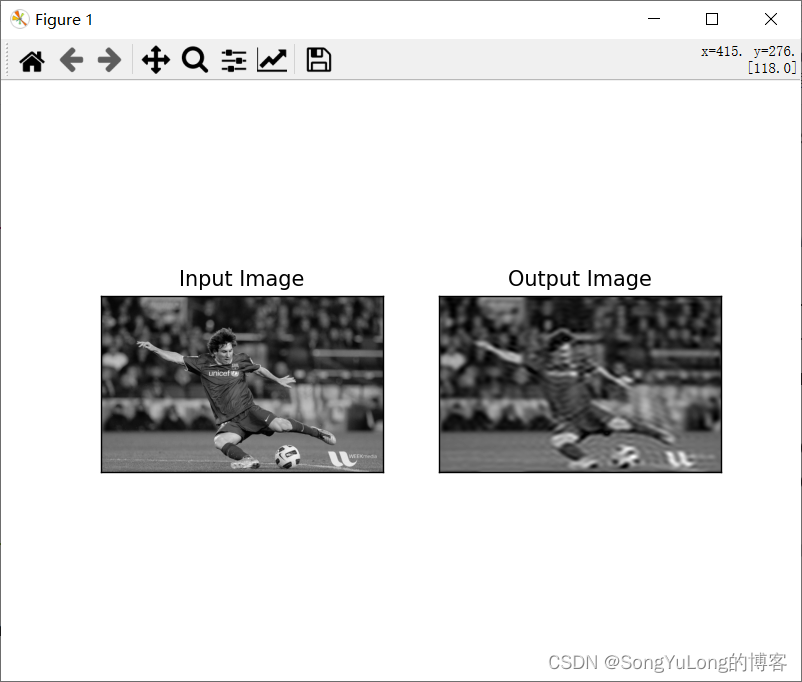
DFT的性能优化
- 当数组的大小为某些值时 DFT 的性能会更好。当数组的大小是 2 的指数时 DFT 效率最高。当数组的大小是 2, 3, 5 的倍数时效率也会很高。所以如果你想提高代码的运行效率时,你可以修改输入图像的大小(补 0)。对于OpenCV 你必须自己手动补 0。但是 Numpy,你只需要指定 FFT 运算的大小,它会自动补 0。
- OpenCV 提供了一个函数:cv2.getOptimalDFTSize()来确定最佳大小。它可以同时被 cv2.dft() 和 np.fft.fft2() 使用。
import numpy as np
import cv2img = cv2.imread('./resource/opencv/image/messi5.jpg', cv2.IMREAD_GRAYSCALE)
rows,cols = img.shape
print('原始图像大小:',rows, cols)
nrows = cv2.getOptimalDFTSize(rows)
ncols = cv2.getOptimalDFTSize(cols)
print('DFT最佳大小:',nrows, ncols)
原始图像大小: 342 548
DFT最佳大小: 360 576
import numpy as np
import cv2
from matplotlib import pyplot as pltimg = cv2.imread('./resource/opencv/image/messi5.jpg', cv2.IMREAD_GRAYSCALE)
rows,cols = img.shape
print('原始图像大小:',rows, cols)
nrows = cv2.getOptimalDFTSize(rows)
ncols = cv2.getOptimalDFTSize(cols)
print('DFT最佳大小:',nrows, ncols)# Numpy数组操作,原图扩大到最佳DFT size
nimg = np.zeros((nrows, ncols))
nimg [:rows, :cols] = img#
right = ncols - cols
bottom = nrows - rows
# just to avoid line breakup in PDF file
mimg = cv2.copyMakeBorder(img, 0, bottom, 0, right, cv2.BORDER_CONSTANT, value=0)plt.subplot(231), plt.imshow(img, cmap='gray')
plt.subplot(232), plt.imshow(nimg, cmap='gray')
plt.subplot(233), plt.imshow(mimg, cmap='gray')
plt.show()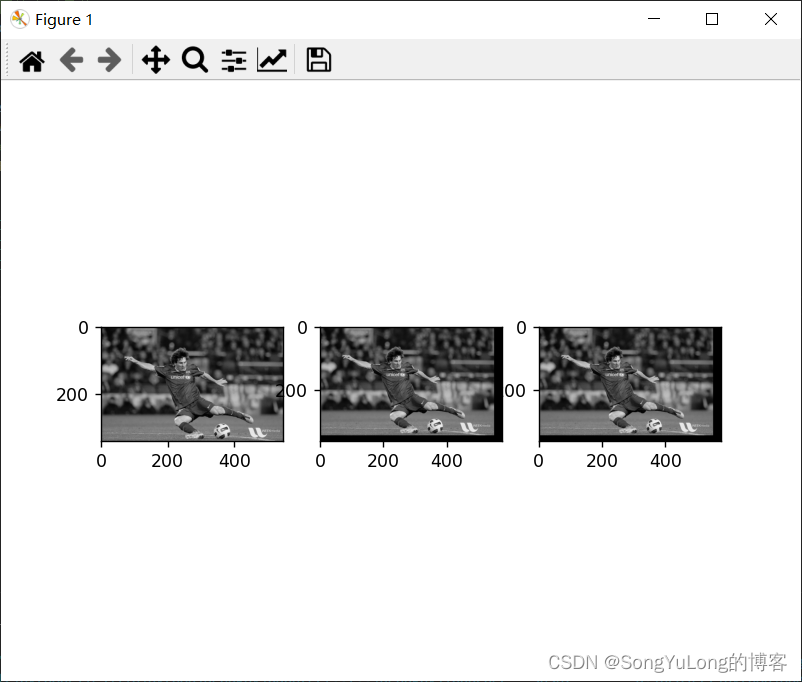
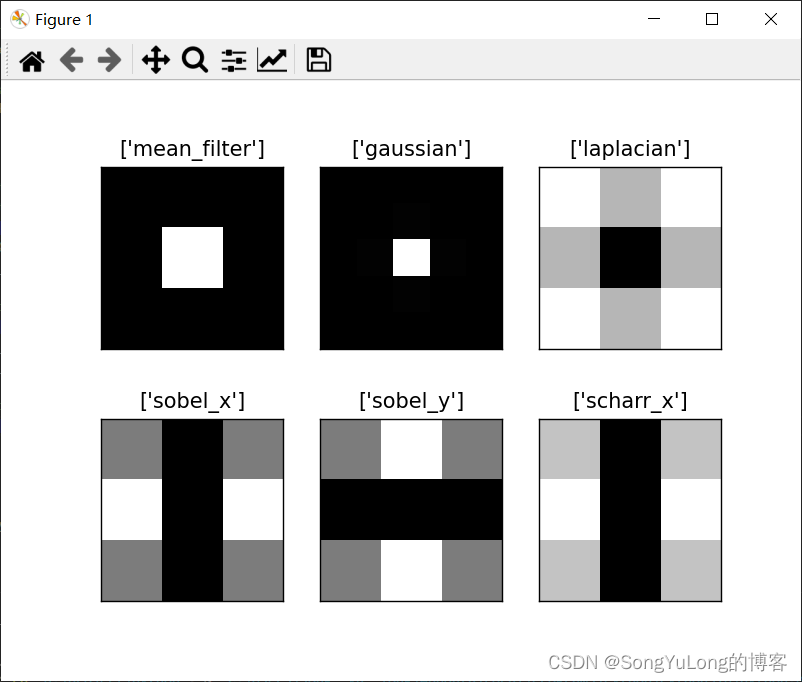
不同滤波算子傅里叶变换对比
为什么拉普拉斯算子是高通滤波器?为什么 Sobel 是 HPF?等等。对于第一个问题的答案我们以傅里叶变换的形式给出。我们一起来对不同的算子进行傅里叶变换并分析它们:
import numpy as np
import cv2
from matplotlib import pyplot as plt# simple averaging filter whitout scaling parameter
mean_filter = np.ones((3,3))# creating a guassian filter
x = cv2.getGaussianKernel(5, 10)
# x.T 为矩阵转置
gaussian = x*x.T# different edge detecting filters
# scharr in x-direction
scharr = np.array([[-3, 0, 3],[-10, 0, 10],[-3, 0, 3]])# sobel in x direction
sobel_x = np.array([[-1, 0, 1],[-2, 0, 2],[-1, 0, 1]])# sobel in y direction
sobel_y = np.array([[-1, -2, -1], [0, 0, 0], [1, 2, 1]])# laplacian
laplacian = np.array([[0, 1, 0], [1, -4, 1],[0, 1, 0]])filters = [mean_filter, gaussian, laplacian, sobel_x, sobel_y, scharr]
filter_name = ['mean_filter', 'gaussian', 'laplacian', 'sobel_x', 'sobel_y', 'scharr_x']fft_filters = [np.fft.fft2(x) for x in filters]
fft_shift = [np.fft.fftshift(y) for y in fft_filters]
mag_spectrum = [np.log(np.abs(z)+1) for z in fft_shift]for i in range(6):plt.subplot(2,3,i+1), plt.imshow(mag_spectrum[i], cmap='gray')plt.title([filter_name[i]]), plt.xticks([]), plt.yticks([])
plt.show()
相关文章:

Python-OpenCV中的图像处理-傅里叶变换
Python-OpenCV中的图像处理-傅里叶变换 傅里叶变换Numpy中的傅里叶变换Numpy中的傅里叶逆变换OpenCV中的傅里叶变换OpenCV中的傅里叶逆变换 DFT的性能优化不同滤波算子傅里叶变换对比 傅里叶变换 傅里叶变换经常被用来分析不同滤波器的频率特性。我们可以使用 2D 离散傅里叶变…...

8.10 用redis实现缓存功能和Spring Cache
什么是缓存? 缓存(Cache), 就是数据交换的缓冲区,俗称的缓存就是缓冲区内的数据,一般从数据库中获取,存储于本地代码。 通过Redis来缓存数据,减少数据库查询操作; 逻辑 每个分类的菜品保存一份缓存数据 数据库菜品数据有变更时清理缓存数据 如何将商品数据缓存起…...
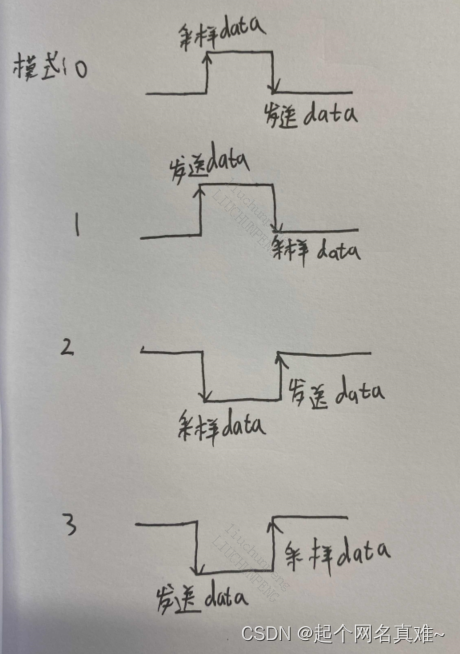
SPI协议个人记录
SPI协议 SPI(Serial Peripheral Interface)是一种同步串行接口技术,由Motorola公司推出。SPI总线系统是一种同步串行外设接口,允许MCU与各种外围设备以串行方式进行通信和数据交换。外围设备包括FLASHRAM、A/D转换器、网络控制器…...

【深度学习 video detect】Towards High Performance Video Object Detection for Mobiles
文章目录 摘要IntroductionRevisiting Video Object Detection BaselinePractice for Mobiles Model Architecture for MobilesLight Flow 摘要 尽管在桌面GPU上取得了视频目标检测的最近成功,但其架构对于移动设备来说仍然过于沉重。目前尚不清楚在非常有限的计算…...

时序预测 | MATLAB实现EEMD-LSTM、LSTM集合经验模态分解结合长短期记忆神经网络时间序列预测对比
时序预测 | MATLAB实现EEMD-LSTM、LSTM集合经验模态分解结合长短期记忆神经网络时间序列预测对比 目录 时序预测 | MATLAB实现EEMD-LSTM、LSTM集合经验模态分解结合长短期记忆神经网络时间序列预测对比效果一览基本介绍模型搭建程序设计参考资料 效果一览 基本介绍 时序预测 | …...
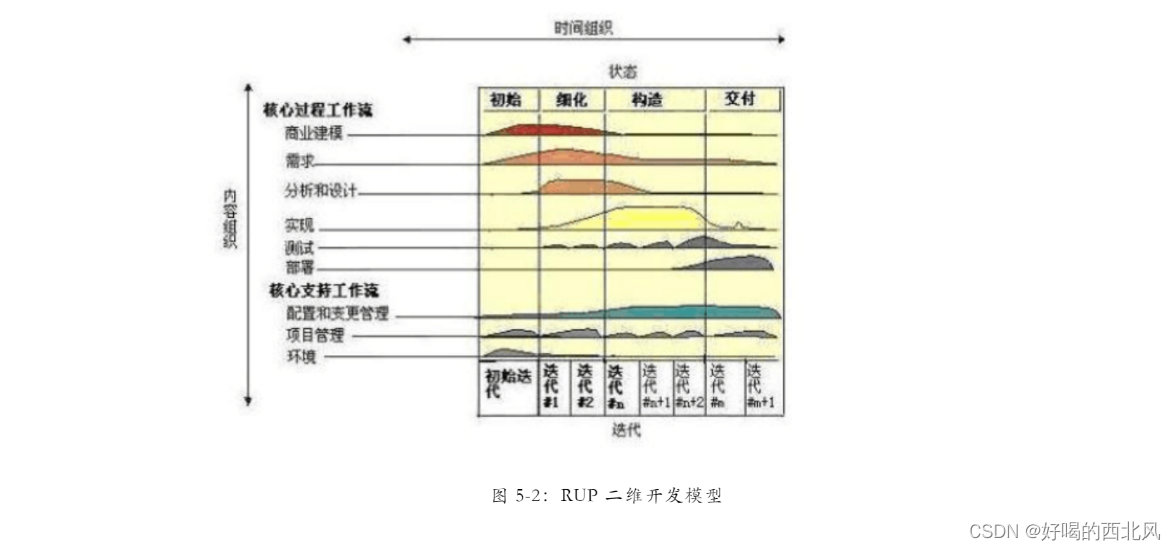
【软件工程】面向对象方法-RUP
RUP(Rational Unified Process,统一软件开发过程)。 RUP特点 以用况驱动的,以体系结构为中心的,迭代增量式开发 用况驱动 用况是能够向用户提供有价值结果的系统中的一种功能用况获取的是功能需求 在系统的生存周期中…...

Golang 的面向对象
文章目录 duck typingnil不一定是空接口组合代替继承接口转换回具体的类型使用switch匹配接口的原始类型 duck typing golang中实现某个接口不需要像其它语言使用 implemet 去继承实现,而是只要你的结构体包含接口所需的方法即可 package mainimport "fmt&qu…...
STABLE DIFFUSION模型及插件的存放路径
记录下学习SD的一些心得,使用的是秋叶大佬的集成webui,下载了之后点击启动器即可开启,文件夹中的内容如下 主模型存放在models文件下的stable-diffusion文件夹内,一些扩展类的插件是存放在extensions文件夹下...
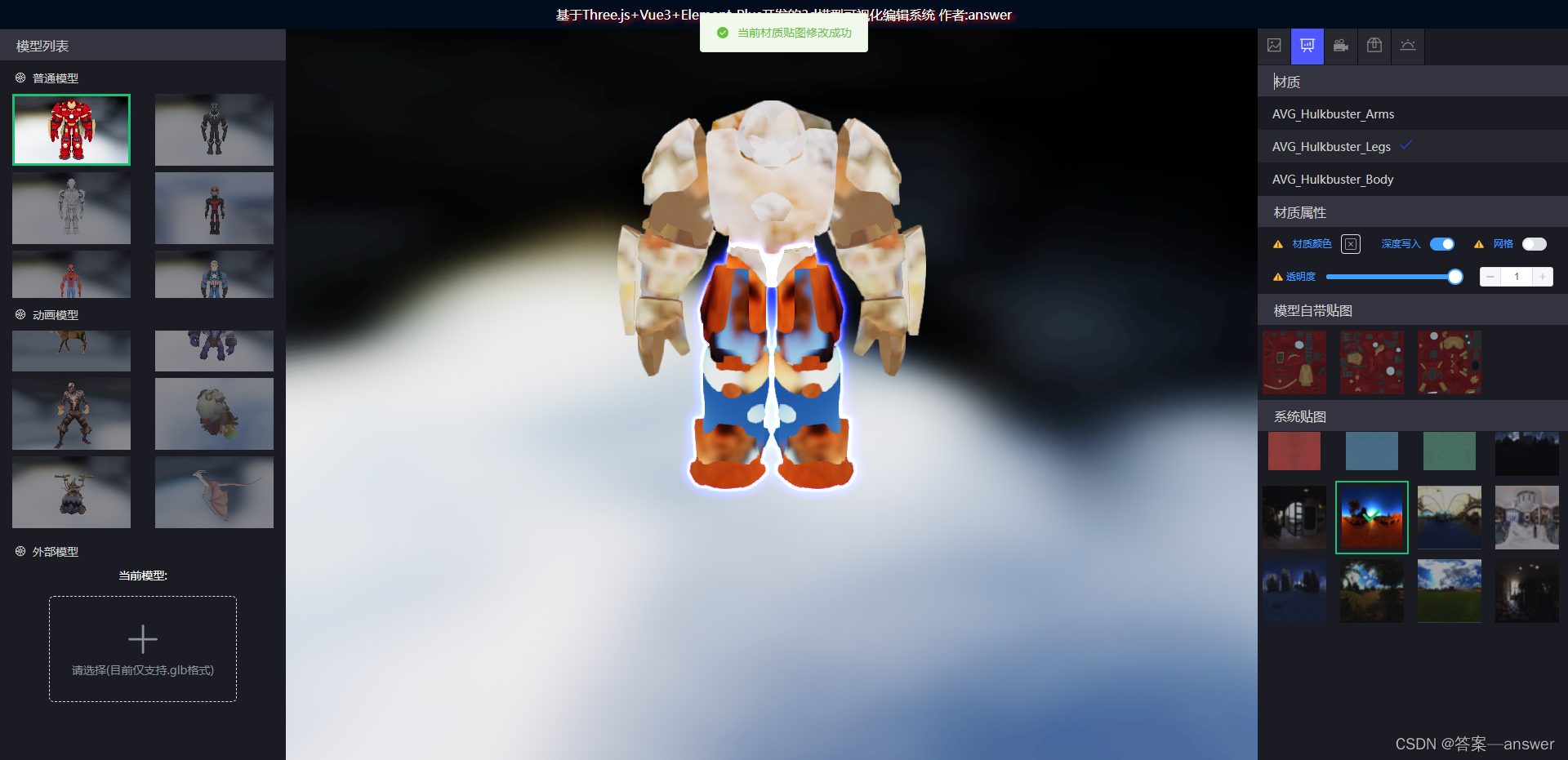
Three.js 设置模型材质纹理贴图和修改材质颜色,材质透明度,材质网格
相关API的使用: 1 traverse (模型循环遍历方法) 2. THREE.TextureLoader(用于加载和处理图片纹理) 3. THREE.MeshLambertMaterial(用于创建材质) 4. getObjectByProperty(通过材…...
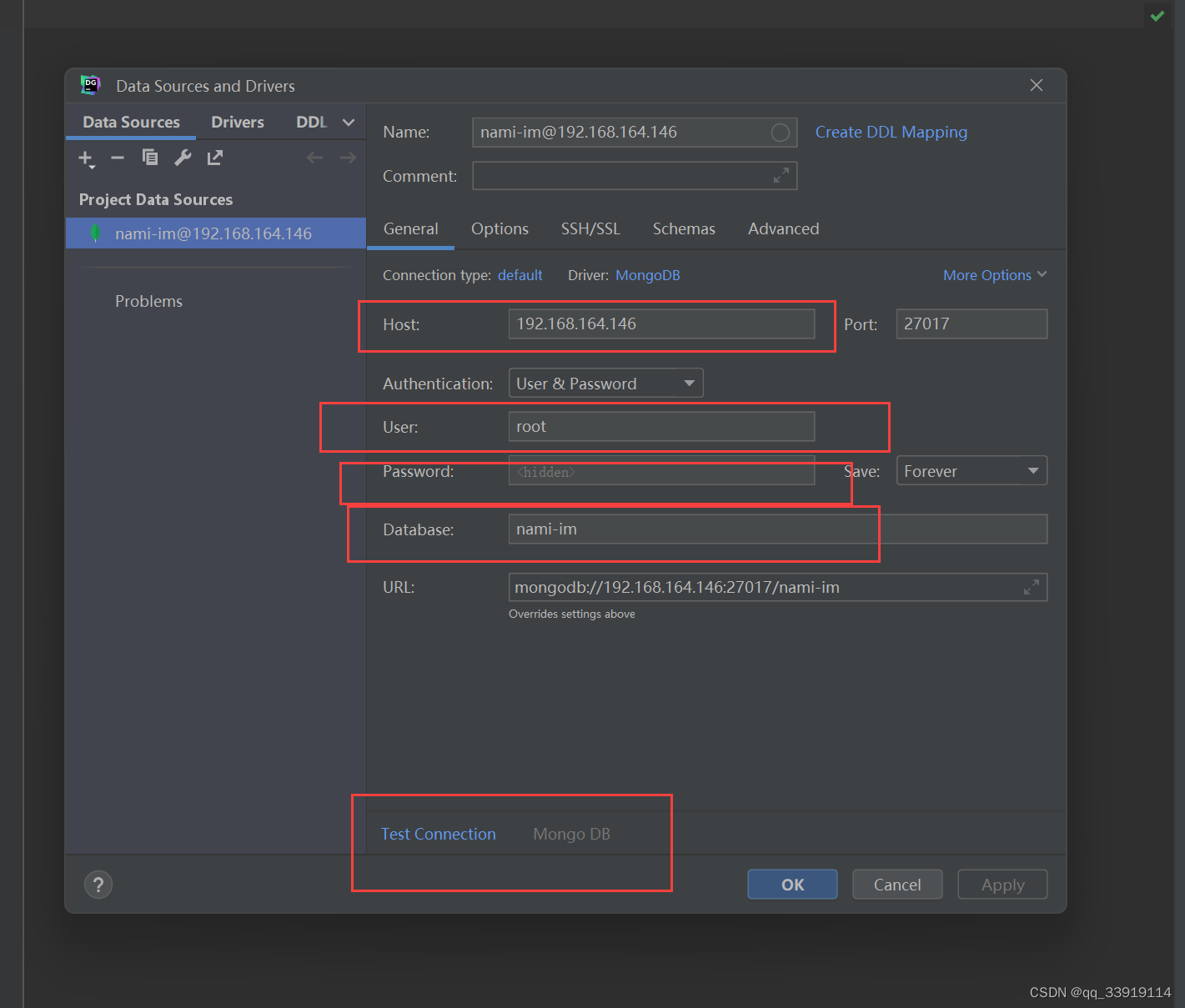
docker 安装mongodb 虚拟机安装mongodb
生产环境直接安装比较好,以及使用集群环境,本文仅测试交流使用,我用来写分布式im测试使用: nami-im: 分布式im, 集群 zookeeper netty kafka nacos rpc主要为gate(长连接服务) logic (业务&…...

在SockJS+Spring Websocket中convertAndSendToUser中的“用户”来自哪里?
目录 一、前言二、Principal三、使用 一、前言 我们知道可以使用客户端订阅的主题前缀从 stomp 服务器向客户端发送消息,例如 /topic/hello。我们还知道我们可以向特定用户发送消息,因为 spring 提供了convertAndSendToUser(username, destination, mes…...
【软件测试】我的2023面试经验谈
最近行业里有个苦涩的笑话:公司扛过了之前的三年,没扛过摘下最近的一年,真是让人想笑又笑不出来。年前听说政策的变化,大家都满怀希望觉得年后行情一片大好,工作岗位激增,至少能有更多的机会拥抱未来。然而…...
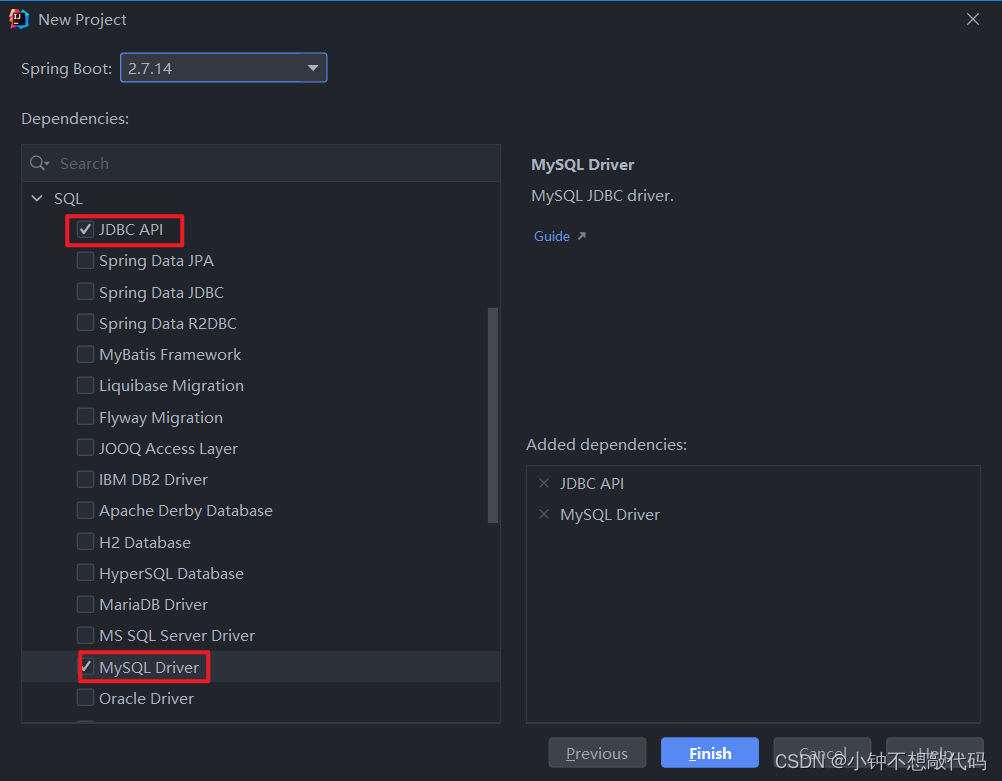
SpringBoot 整合JDBC
SpringData简介 Sping Data 官网:https://spring.io/projects/spring-data数据库相关的启动器 :可以参考官方文档:https://docs.spring.io/spring-boot/docs/2.6.5/reference/htmlsingle/#using-boot-starter 整合JDBC 创建测试项目测试数据…...
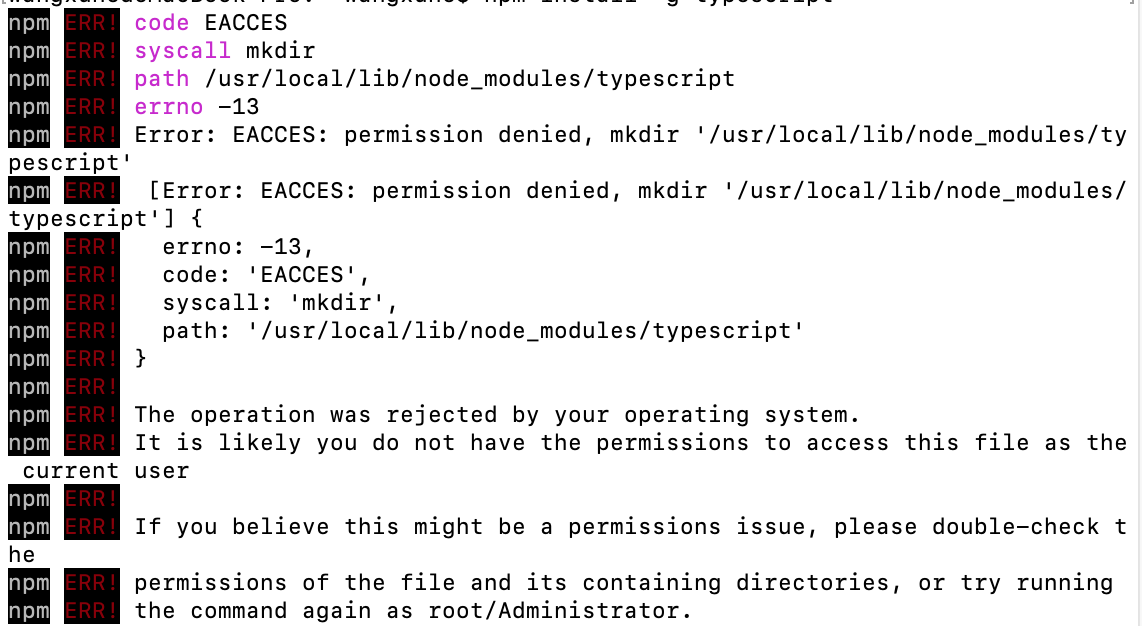
TypeScript使用npm安装报错问题
问题如图: 问题原因: 权限不足导致,可以输入如下命令: sudo npm install i -g typescript该命令会要求输入登录密码相关,稍等片刻,即可安装成功。检测安装的命令: tsc -v...

2023国赛数学建模思路 - 复盘:人力资源安排的最优化模型
文章目录 0 赛题思路1 描述2 问题概括3 建模过程3.1 边界说明3.2 符号约定3.3 分析3.4 模型建立3.5 模型求解 4 模型评价与推广5 实现代码 建模资料 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 描述 …...

学习pytorch 3 tensorboard的使用
tensorboard的使用 1. 安装2. add_scalar 查看函数图形3. 查看结果4. add_image() 查看训练步骤中间结果的图片 1. 安装 pytorch conda环境 pip install tensorboard pip install opencv-python2. add_scalar 查看函数图形 常用来查看 train val loss等函数图形 from torch…...

Linux 命令篇
一、启动网络命令 ip addr 查看网卡信息 service network start 启动网卡 service network stop 关闭网卡 service network restart 重启网络 二、pwd 命令 查看当前目录的路径 linux 下所有的绝对路径都是从根目录 "/" 开始 root:是linux下root用户的根目…...

OpenCV-SIFT算法详解
系列文章目录 文章目录 系列文章目录引言一、高斯金字塔二、高斯差分金字塔三、特征点处理四、特征点描述子总结 引言 SIFT算法是为了解决图片的匹配问题,想要从图像中提取一种对图像的大小和旋转变化保持鲁棒的特征,从而实现匹配。这一算法的灵感也十分…...

Java中的接口到底是什么?
要说Java的【接口】,可以将其类比为现实生活中的一种约定或规范。在Java中,接口定义了一组方法的集合,但没有提供这些方法的具体实现。 你可以将接口看作是一个合同,它规定了一个类必须实现的一组方法。这些方法描述了类所需具备…...
Jpa与Druid线程池及Spring Boot整合(一): spring-boot-starter-data-jpa 搭建持久层
Jpa与Druid线程池及Spring Boot整合(一) Jpa与Druid线程池及Spring Boot整合(二):几个坑 附录官网文档:core.domain-events域事件 (一)Jpa与Druid连接池及Spring Boot整合作为持久层,遇到系列问题,下面一 一记录: pom.xml 文件中加入必须的…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...
