2023国赛数学建模思路 - 复盘:人力资源安排的最优化模型
文章目录
- 0 赛题思路
- 1 描述
- 2 问题概括
- 3 建模过程
- 3.1 边界说明
- 3.2 符号约定
- 3.3 分析
- 3.4 模型建立
- 3.5 模型求解
- 4 模型评价与推广
- 5 实现代码
- 建模资料
0 赛题思路
(赛题出来以后第一时间在CSDN分享)
https://blog.csdn.net/dc_sinor?type=blog
1 描述
某大学数学系人力资源安排问题是一个整数规划的最优化问题,通过具体分析数学系现有的技术力量和各方面的约束条件,在问题一的求解中,可以列出一天最大直接收益的整数规划,求得最大的直接收益是42860元;而在问题二的求解中,由于教授一个星期只能工作四天,副教授一个星期只能工作五天,在这样的约束条件下,列出一个星期里最大直接收益的整数规划模型,求得其最大直接收益是198720元。
2 问题概括
数学系的教师资源有限,现有四个项目来源于四个不同的客户,工作的难易程度不一,各项目对有关技术人员的报酬不同。所以:
1.在满足工作要求的情况下,如何分配数学系现有的技术力量,使得其一天的直接收益最大?
2.在教授与副教授工作时间受到约束的条件下,如何分配数学系现有的技术力量,使得其在一个星期里的直接收益最大?
3 建模过程
3.1 边界说明
1.不同技术力量的人每天被安排工作的几率是相等的,且相同职称的个人去什么地方工作是随机的;
2.客户除了支付规定的工资额外,在工作期间里,还要支付所有相关的花费(如餐费,车费等);
3.当天工作当天完成.
3.2 符号约定

3.3 分析
由题意可知各项目对不同职称人员人数都有不同的限制和要求.对客户来说质量保证是关键,而教授相对稀缺,因此各项目对教授的配备有不能少于一定数目的限制.其中由于项目技术要求较高,助教不能参加.而两项目主要工作是在办公室完成,所以每人每天有50元的管理费开支.
由以上分析可得:最大直接收益=总收益-技术人员工资-、两地保管费.
3.4 模型建立



3.5 模型求解
相关数据表格如下:
数学系的职称结构及工资情况
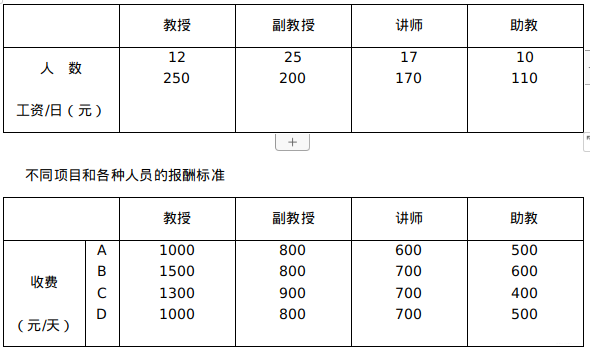
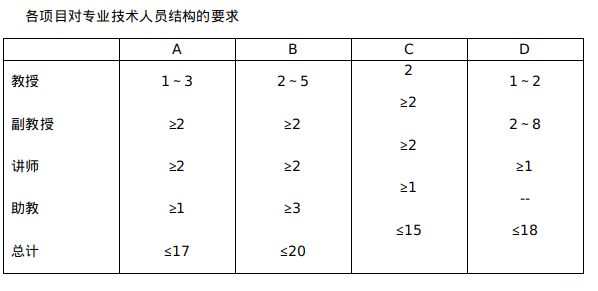
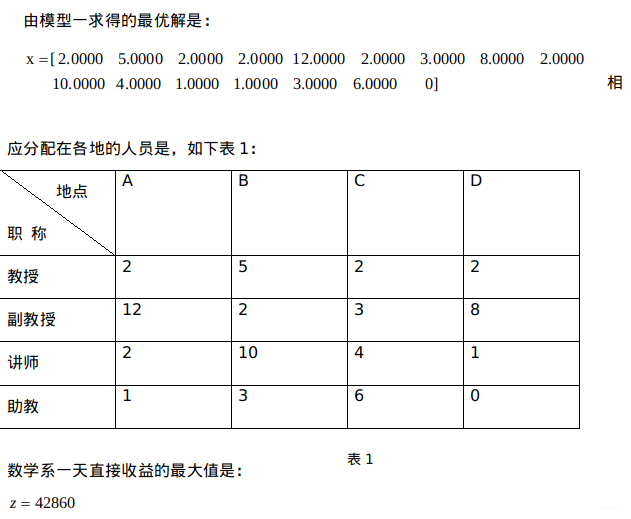
4 模型评价与推广
本模型通过合理的假设,充分考虑各方面的限制条件,得出的人员安排和直接收益
都是本模型的最优解与最优值,对武汉大学数学系的人力资源安排有一定的指导作用。但从模型假设中,我们可以知道对数
学系现有的技术力量的安排是随机的,在相同工作时段里,可能会出现部分人工作次数较多,而部分人较少的不公平情况。
所以在满足工作需求的情况下,分配工作时应该要人为地尽量使得每个人的工作次数不要相差太远,或者相等。
此模型通过对人力资源的调配,从量化的角度得出数学系的最大直接收益。利用此模型的方法可以求出所有类似本模型的线性规划模型。但是,本模型只是单目标的规划,可以在此基础上,增加目标要求。如在数学系的直接收益尽可能大的基础上,使得客户所花费的资金最少,等等。从而建立多目标规划模型。解决更为复杂的实际问题。
5 实现代码
f=[-1000;-800;-550;-450;-1500;-800;-650;-550;-1300;-900;-650;-350;-1000;-800;-650;-450];
A=zeros(9,16);
for i=1:1for j=1:16A(i,j)=1; end
end
for i=2:5for j=i-1:4:11+iA(i,j)=1;end
end
i0=0;
for i=6:9for j=i0+1:(i-5 )*4A(i,j)=1;endi0=j;
end
b=[64;17;20;15;18;12;25;17;10];
Aeq=zeros(1,16);
Aeq(1,3)=1;
beq=[2];
LB=[1;2;2;1;2;2;2;2;2;2;2;1;1;3;1;0];
UB=[3;5;2;2;inf;inf;inf;8;inf;inf;inf;inf;inf;inf;inf;0];
[x,fval]=linprog(f,A,b,Aeq,beq,LB,UB)f=[-1000;-1000;-1000;-1000;-1000;-1000;-1000;-1500;-1500;-1500;-1500;-1500;-1500;-1500;-1250;-1250;-1250;-1250;-1250;-1250;-1250;-950;-950;-950;-950;-950;-950;-950;-800;-800;-800;-800;-800;-800;-800;-800;-800;-800;-800;-800;-800;-800;-850;-850;-850;-850;-850;-850;-850;-750;-750;-750;-750;-750;-750;-750;-600;-600;-600;-600;-600;-600;-600;-700;-700;-700;-700;-700;-700;-700;-650;-650;-650;-650;-650;-650;-650;-650;-650;-650;-650;-650;-650;-650;-500;-500;-500;-500;-500;-500;-500;-600;-600;-600;-600;-600;-600;-600;-350;-350;-350;-350;-350;-350;-350;-450;-450;-450;-450;-450;-450;-450];
A=zeros(60,112);
for i=1;1for j=1:112A(i,j)=1;end
end
i0=0;
for i=2:4for j=i0+1:(i-1)*28A(i,j)=1;endi0=j;
end
for i=5:32for j=(i-4):28:80+iA(i,j)=1;end
end
for i=33:39for j= i-32:7:(i-11)A(i,j)=1;end
end
j0=j;
for i=40:46for j=j0+(i-39):7:(i-18)+j0A(i,j)=1;end
end
j0=j;
for i=47:53for j=j0+(i-46):7:j0+(i-25)A(i,j)=1;end
end
j0=j;
for i=54:60for j=j0+(i-53):7:j0+(i-32)A(i,j)=1;end
end
b=[362;48;125;119;17;17;17;17;17;17;17;20;20;20;20;20;20;20;15;15;15;15;15;15;15;18;18;18;18;18;18;18;12;12;12;12;12;12;12;25;25;25;25;25;25;25;17;17;17;17;17;17;17;10;10;10;10;10;10;10];
UB=[3;3;3;3;3;3;3;5;5;5;5;5;5;5;3;3;3;3;3;3;3;2;2;2;2;2;2;2;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;8;8;8;8;8;8;8;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;0;0;0;0;0;0;0];
LB=[1;1;1;1;1;1;1;2;2;2;2;2;2;2;1;1;1;1;1;1;1;1;1;1;1;1;1;1;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;1;1;1;1;1;1;1;1;1;1;1;1;1;1;3;3;3;3;3;3;3;1;1;1;1;1;1;1;0;0;0;0;0;0;0];
Aeq=zeros(7,112);
for i=1:7Aeq(i,i+14)=1;
end
beq=[2;2;2;2;2;2;2];
[x,fval]=linprog(f,A,b,Aeq,beq,LB,UB)
建模资料
资料分享: 最强建模资料


相关文章:

2023国赛数学建模思路 - 复盘:人力资源安排的最优化模型
文章目录 0 赛题思路1 描述2 问题概括3 建模过程3.1 边界说明3.2 符号约定3.3 分析3.4 模型建立3.5 模型求解 4 模型评价与推广5 实现代码 建模资料 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 描述 …...

学习pytorch 3 tensorboard的使用
tensorboard的使用 1. 安装2. add_scalar 查看函数图形3. 查看结果4. add_image() 查看训练步骤中间结果的图片 1. 安装 pytorch conda环境 pip install tensorboard pip install opencv-python2. add_scalar 查看函数图形 常用来查看 train val loss等函数图形 from torch…...

Linux 命令篇
一、启动网络命令 ip addr 查看网卡信息 service network start 启动网卡 service network stop 关闭网卡 service network restart 重启网络 二、pwd 命令 查看当前目录的路径 linux 下所有的绝对路径都是从根目录 "/" 开始 root:是linux下root用户的根目…...

OpenCV-SIFT算法详解
系列文章目录 文章目录 系列文章目录引言一、高斯金字塔二、高斯差分金字塔三、特征点处理四、特征点描述子总结 引言 SIFT算法是为了解决图片的匹配问题,想要从图像中提取一种对图像的大小和旋转变化保持鲁棒的特征,从而实现匹配。这一算法的灵感也十分…...

Java中的接口到底是什么?
要说Java的【接口】,可以将其类比为现实生活中的一种约定或规范。在Java中,接口定义了一组方法的集合,但没有提供这些方法的具体实现。 你可以将接口看作是一个合同,它规定了一个类必须实现的一组方法。这些方法描述了类所需具备…...
Jpa与Druid线程池及Spring Boot整合(一): spring-boot-starter-data-jpa 搭建持久层
Jpa与Druid线程池及Spring Boot整合(一) Jpa与Druid线程池及Spring Boot整合(二):几个坑 附录官网文档:core.domain-events域事件 (一)Jpa与Druid连接池及Spring Boot整合作为持久层,遇到系列问题,下面一 一记录: pom.xml 文件中加入必须的…...
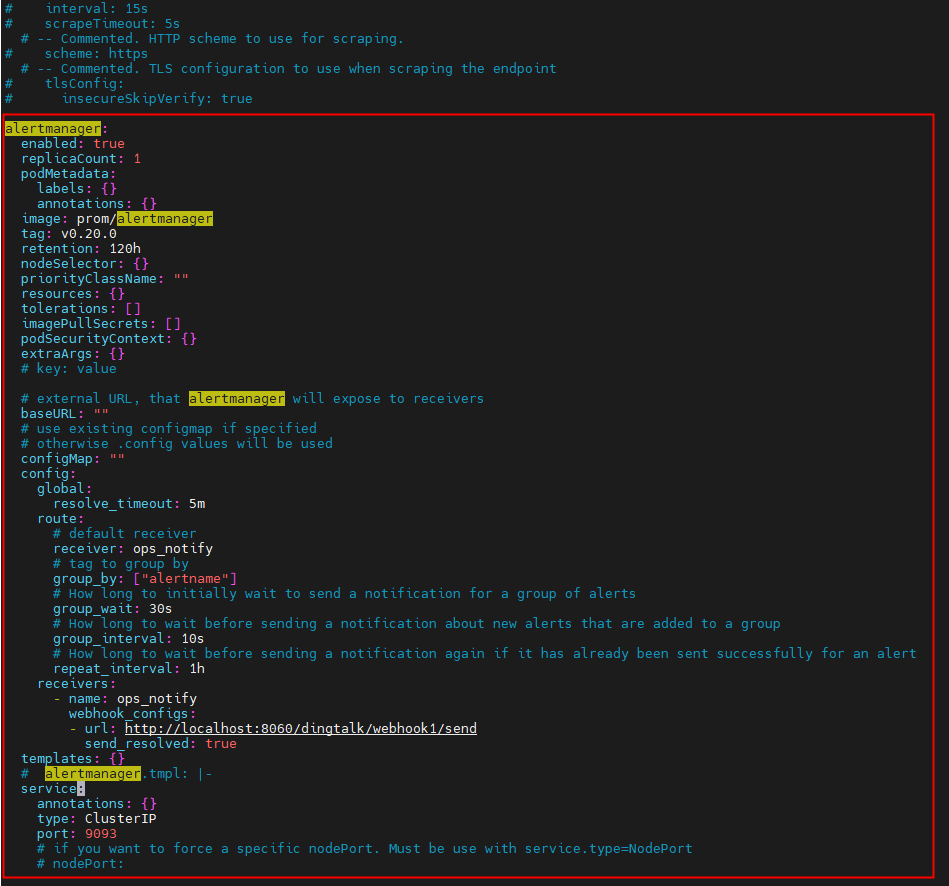
helm部署vmalert
先决条件 安装以下软件包:git, kubectl, helm, helm-docs,请参阅本教程。 在 CentOS 上启用 snap 并安装 helm 启用 snapd 使用以下命令将 EPEL 存储库添加到您的系统中: sudo yum install epel-release 按如下方式安装 Snap࿱…...

加工厂数字孪生3D可视化展示系统重塑管理模式
近年来“数字化转型”成立各行业聚焦的发展方向,在工业制造领域,智慧工业数字孪生可视化平台作为一种新型的技术手段,或将成为助力企业跑赢数字化转型最后一公里。 提高生产效率 传统的生产方式往往需要大量的人工干预,不仅耗时耗…...

php从静态资源到动态内容
1、从HTML到PHP demo.php:后缀由html直接改为php,实际上当前页面已经变成了动态的php应用程序脚本 demo.php: 允许通过<?php ... ?>标签,添加php代码到当前脚本中 php标签内部代码由php.exe解释, php标签之外的代码原样输出,仍由web服务器解析 <!DOCTYPE html>…...

JavaScript:模块化【CommonJS与ES6】
在 JavaScript 编程中,随着项目的复杂性增加,代码的组织和管理变得至关重要。模块化是一种强大的编程概念,它允许我们将代码划分为独立的模块,提高了可维护性和可扩展性。本文将详细介绍 CommonJS 和 ES6 模块,帮助你理…...
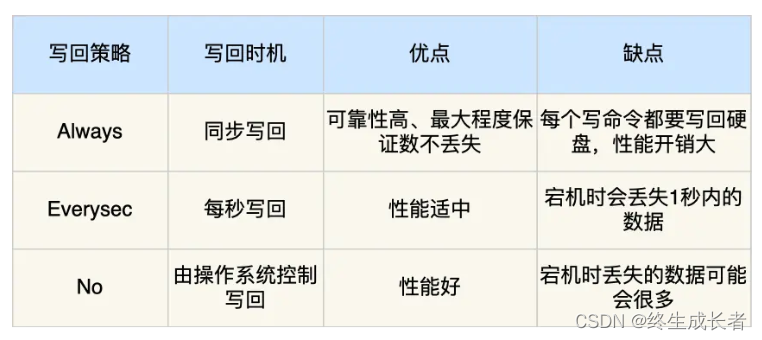
Redis—持久化
这里写目录标题 AOF三种写回策略写回策略的优缺点AOF 重写机制AOF后台重写AOF优缺点使用命令 RDBRDB 持久化的工作原理执行快照时,数据能被修改吗RDB 持久化的优点RDB 持久化的缺点 混合持久化大key对持久化的影响 AOF 保存写操作命令到日志的持久化方式࿰…...
【设计模式】代理模式
在代理模式(Proxy Pattern)中,一个类代表另一个类的功能。这种类型的设计模式属于结构型模式。 在代理模式中,我们创建具有现有对象的对象,以便向外界提供功能接口。 介绍 意图:为其他对象提供一种代理以…...

mac arm 通过brew搭建 php+nginx+mysql+xdebug
1.安装nginx brew install nginx //安装brew services start nginx //启动2.安装php brew install php7.4 //安装export PATH"/opt/homebrew/opt/php7.4/bin:$PATH" //加入环境变量 export PATH"/opt/homebrew/opt/php7.4/sbin:$PATH"brew serv…...

软信天成:告别手动编码,实现智能自动化云数据管理
数字化转型浪潮之下,各个企业都在大力投资新的基于云的流程、平台和环境,以期获取可扩展性、弹性、敏捷性和成本效益等优势。 这些趋势要求企业IT部门能够帮助组织,在对分析进行现代化改造的过程中达到云就绪或云优先状态。事实上࿰…...
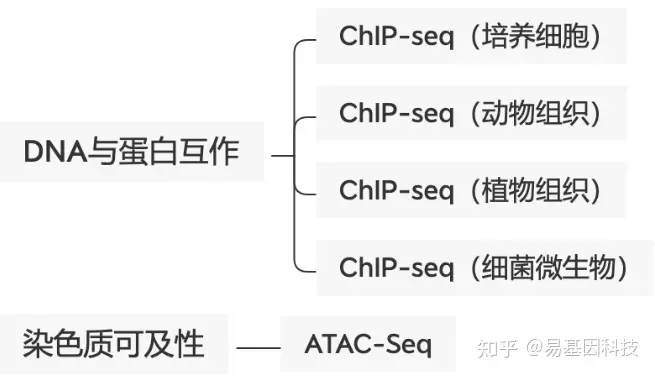
易基因:ChIP-seq等揭示转录因子NRF1调控原始生殖细胞发育、增殖和存活的表观遗传机制|科研进展
大家好,这里是专注表观组学十余年,领跑多组学科研服务的易基因。 原始生殖细胞(Primordial germ cell,PGC)是生殖细胞前体,可以产生卵母细胞和精子,确保生命延续。尽管PGC特化(PGC …...

35岁,体能断崖?你需要健康的生活习惯
大厂裁员,称35岁以后体能下滑,无法继续高效率地完成工作;体重上涨,因为35岁以后新陈代谢开始变慢;甚至坐久了会腰疼、睡眠困扰开始加重,在众多的归因中,35岁的到来,为一切的焦虑埋下…...

mysql 习题总结
1.select sex,avg(salsry) as 平均薪资 from emp group by sex; 2.select depart,sum(salsry) from emp group by depart; 3.select depart ,sum(salary) from emp group by depart order by sum(salary) desc limit 1,1; 4.select name from emp group by name having count(n…...

IL汇编语言做一个窗体
网上看到一段代码, .assembly extern mscorlib {} .assembly Classes { .ver 1:0:1:0 } .namespace MyForm { .class public TestForm extends [System.Windows.Forms]System.Windows.Forms.Form { .field private class [System]…...
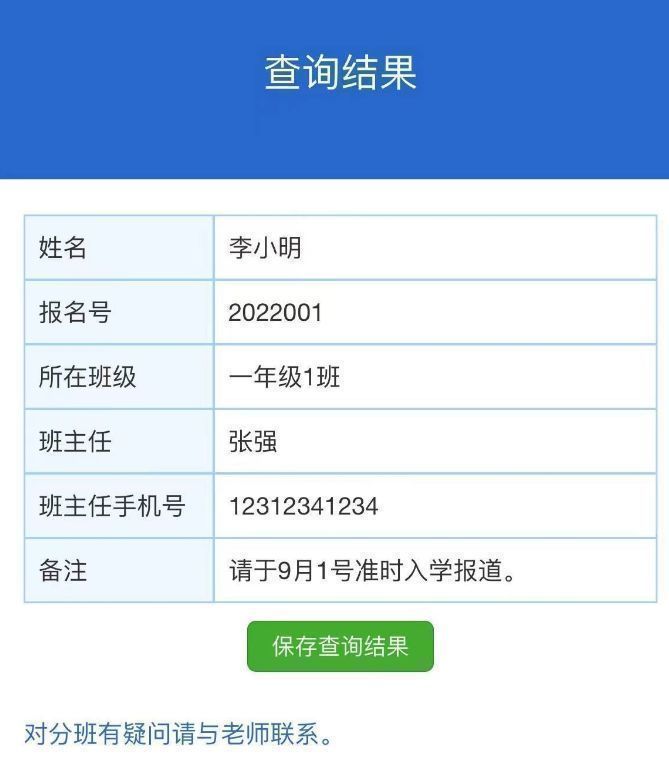
不用技术代码,分班查询系统怎么做?
暑假即将结束,新学期开始将面临分班信息公布的工作!对于分班信息公布,涉及到学生的个人信息,包括姓名、学号、班级等。在发布这些信息时,必须确保数据的保密性,防止未经授权的人员获取到学生的个人信息。因…...

【Mybatis】调试查看执行的 SQL 语句
1. 问题场景: 记录日常开发过程中 Mybatis 调试 SQL 语句,想要查看Mybatis 中执行的 SQL语句,导致定位问题困难 2. 解决方式 双击shift找到mybatis源码中的 MappedStatement的getBoundSql()方法 public BoundSql getBoundSql(Object para…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...
