OpenCV-SIFT算法详解
系列文章目录
文章目录
- 系列文章目录
- 引言
- 一、高斯金字塔
- 二、高斯差分金字塔
- 三、特征点处理
- 四、特征点描述子
- 总结
引言
SIFT算法是为了解决图片的匹配问题,想要从图像中提取一种对图像的大小和旋转变化保持鲁棒的特征,从而实现匹配。这一算法的灵感也十分的直观:人眼观测两张图片是否匹配时会注意到其中的典型区域(特征点部分),如果我们能够实现这一特征点区域提取过程,再对所提取到的区域进行描述就可以实现特征匹配了。于是问题就演变成了以下几个子问题:
应该选取什么样的点作为特征点呢?:人眼对图像中的高频区域更加的敏感,由此我们应该选择变化剧烈的边缘或者角点进行检测,这里我们选择检测角点。(这里的intuition不是很明白,但感觉来说可能是我们提取的是特征点进行匹配,而边缘往往是由多个点组成。)
怎样使得选取的特征点有尺度不变性呢?:使用高斯金字塔获取不同尺寸下的图像变体,由这些变体获得尺度不变特征。
怎样使得选取的特征点有缩放不变性呢?:使用高斯金字塔获取不同尺寸下的图像变体,每个变体里都提取特征点再缩放回原大小以获得图像不同尺寸下的特征点。
怎样使得选取的特征点有旋转不变性呢?:后续采取将特征点区域旋转到主方向的设定以获得旋转不变性。
如何描述特征点区域呢?: 使用特征点区域内每个方向的梯度赋值,类似HOG算子。
以上几个问题在SIFT算法里都用了很有意思的trick,后续会一一介绍。
一、高斯金字塔
引入高斯金字塔的目的在引言中已经介绍过了–解决图片缩放及尺度变化下特征提取的问题,高斯金字塔的Intuition有两个:1. 人看物体时近大远小,可以对图片下采样实现(金字塔->组);2. 人看物体时近处清晰,远处模糊,可以对图像高斯平滑实现(高斯->层);具体的推导可以参见我的另一篇博客:
Opencv学习笔记(六)图像金字塔
在SIFT里,高斯金字塔的层数和组数有着如下设定:
组数: O = [ l o g 2 m i n ( M , N ) ] − 3 O=[log_2min(M,N)]-3 O=[log2min(M,N)]−3
层数: S = n + 3 S=n+3 S=n+3
组数的设定是来自于提出SIFT算法的原始论文给出的经验值,理论上来说知要 O ≤ [ l o g 2 m i n ( M , N ) ] O\leq[log_2min(M,N)] O≤[log2min(M,N)]即可,层数的设定则是有着理论依据的,这里的 n n n是我们想要提取特征点的图片层数,由于提取出高斯金字塔后需要计算层间差分以获得高斯差分金字塔(DOG, Difference of Gausssian),高斯金字塔层数需要比DOG层数多1,而计算特征值时要求在尺度层面,即上下相邻层间计算,则DOG层数要比特征层数多2,则要求 S = n + 3 S=n+3 S=n+3。
附:在SIFT中对于高斯金字塔有几个需要补充的知识点。
SIFT算法中的S指的是"scale"即尺度的概念,这一概念有别于传统的图像尺寸,而是一种连续变化的参数,在高斯金字塔里的 σ \sigma σ就是这样一个尺度空间的参数,更特殊的,高斯核是唯一可以产生连续多尺度变化的线性核,这就是为什么我们用高斯金字塔,这一部分内容涉及到尺度空间的概念,可以自行了解。
图像金子塔一文中提到了两个基础参数,层间尺度变化系数 k k k和初始尺度 σ 0 \sigma_0 σ0,在原始算法中规定 k = 2 o + r n , r = 0 , 1… , n + 2 k=2^{o+\frac{r}{n}},r={0,1…,n+2} k=2o+nr,r=0,1…,n+2,由于每组的起始层是由前一组倒数第三层降采样得到,实际上保证了每组开始的尺度为 σ 0 , 2 σ 0 , 3 σ 0 . . . \sigma_0,2\sigma_0,3\sigma_0… σ0,2σ0,3σ0…。此外我们提到 σ 0 = 1.6 \sigma_0=1.6 σ0=1.6,而实际拍摄图片时相机已经原始景物进行了一次尺度变换,此变换的系数原文设定经验值为 σ ′ = 0.5 \sigma’=0.5 σ′=0.5,由此我们得到 σ 0 = 1. 6 2 − σ ′ 2 = 1.52 \sigma_0=\sqrt{1.62-\sigma’2}=1.52 σ0=1.62−σ′2
=1.52。这一式子的来历为:高斯滤波体现为高斯核与原图进行卷积 f ( x ) ⨂ G ′ ( x ) f(x)\bigotimes G’(x) f(x)⨂G′(x),两次高斯滤波的级联相当于 f ( x ) ⨂ ( G ′ ( x ) ⨂ G ( x ) ) f(x)\bigotimes (G’(x) \bigotimes G(x)) f(x)⨂(G′(x)⨂G(x)),而两个高斯卷积的结果仍为高斯卷积,且方差满足平方和关系,可用时域卷积或者傅里叶变换证明,详见参考文献。
二、高斯差分金字塔
通过高斯金字塔,我们获取了不同尺度的图片,接下来的问题是如何获取高频区域呢,一个很简单的思路就是按照边缘检测的算法使用差分滤波器如拉普拉斯滤波器、sobel滤波器在图片上滑动找到灰度值变化剧烈的区域。而经前人研究,归一化的高斯拉普拉斯算子的极大值极小值相较于其他特征提取函数可以获得最稳定的图像特征,因此我们打算使用归一化的高斯拉普拉斯算子在多尺度图片上提取特征,但是使用这种方式提取复杂度会很高,又尺度归一化高斯拉普拉斯算子和DOG函数有着如下关系:
G ( x , y , k σ ) − G ( x , y , σ ) ≈ ( k − 1 ) σ 2 ∇ 2 G G(x,y,k\sigma)-G(x,y,\sigma)\approx(k-1)\sigma^2 \nabla^2 G G(x,y,kσ)−G(x,y,σ)≈(k−1)σ2∇2G
证明如下:
忽略高斯函数系数:
G ( x , y , σ ) = 1 σ 2 e x p ( − x 2 + y 2 2 σ 2 ) ∂ G ∂ x = − x σ 4 e x p ( − x 2 + y 2 2 σ 2 ) ∂ 2 G ∂ x 2 = − σ 2 + x 2 σ 6 e x p ( − x 2 + y 2 2 σ 2 ) ∇ 2 G ( x , y ) = ∂ 2 G ∂ x 2 + ∂ 2 G ∂ y 2 = − 2 σ 2 + x 2 + y 2 σ 6 e x p ( − x 2 + y 2 2 σ 2 ) ∂ G ∂ σ = − 2 σ 2 + x 2 + y 2 σ 5 e x p ( − x 2 + y 2 2 σ 2 ) ⇒ σ ∇ 2 G = ∂ G ∂ σ
G(x,y,σ)=1σ2exp(−x2+y22σ2)∂G∂x=−xσ4exp(−x2+y22σ2)∂2G∂x2=−σ2+x2σ6exp(−x2+y22σ2)∇2G(x,y)=∂2G∂x2+∂2G∂y2 =−2σ2+x2+y2σ6exp(−x2+y22σ2)∂G∂σ=−2σ2+x2+y2σ5exp(−x2+y22σ2)⇒σ∇2G=∂G∂σ
G(x,y,σ)=σ21exp(−2σ2x2+y2)∂x∂G=−σ4xexp(−2σ2x2+y2)∂x2∂2G=σ6−σ2+x2exp(−2σ2x2+y2)∇2G(x,y)=∂x2∂2G+∂y2∂2G =σ6−2σ2+x2+y2exp(−2σ2x2+y2)∂σ∂G=σ5−2σ2+x2+y2exp(−2σ2x2+y2)⇒σ∇2G=∂σ∂G
又对于差分高斯金字塔有:
D O G = G ( x , y , k σ ) − G ( x , y , σ ) ( k − 1 ) σ ≈ ∂ G ∂ σ D O G ≈ ( k − 1 ) σ 2 ∇ 2 G \begin{aligned} &DOG=\frac{G(x,y,k\sigma)-G(x,y,\sigma)}{(k-1)\sigma}\approx \frac{\partial G}{\partial \sigma}\ & DOG \approx(k-1)\sigma2\nabla2G \end {aligned} DOG=(k−1)σG(x,y,kσ)−G(x,y,σ)≈∂σ∂GDOG≈(k−1)σ2∇2G
由此我们不再需要在高斯金子塔上进行卷积操作,只需要计算在尺度层面 σ \sigma σ进行层间差分得到高斯差分金字塔(DOG),即完成了特征提取的操作。
在这里插入图片描述
三、特征点处理
得到DOG后,我们理论上来说就已经获得了特征值,但我们需要对特征值进行一些处理,就像我们在cannny边缘检测中使用的非极大值抑制等思路,去掉没那么特征的特征值。
1.阈值化
简单的阈值化去除掉变换没有那么剧烈的点,这些点就有可能是噪声引起的,算是在高斯拉普拉斯之外又加了一层去噪措施。
v a l = { v a l a b s ( v a l ) > 0.5 T n 0 o t h e r w i s e val=
{val0abs(val)>0.5Tnotherwise
val={val0abs(val)>0.5nTotherwise
这里的 T T T为经验值0.04, n n n为之前提过的提取特征点数目。
2.非极大值抑制
非极大值一致的思路就和在其他算法中的一样,我们要求选取出的特征值应该是其领域范围内的极值,不同之处在于其他算法要求的只是图像这一二维平面内的极值,而这里要求还要在尺度 σ \sigma σ这一层面上也是极值,这也承接了前文DOG层数要比提取特征所用层数多2的设定。
在这里插入图片描述
3. 二阶泰勒修正
由于我们的图片在 x , y , σ x,y,\sigma x,y,σ方向上都只能取到离散值,即使通过前两个步骤取到了一些特征点,但这些特征点都不够精确,我们需要引入二阶泰勒函数对齐进行修正,使得特征点可以出现在亚像素(亚尺度)位置。
在这里插入图片描述
f ( X ) = f ( X 0 ) + ∂ f T ∂ X X ^ + 1 2 X T ^ ∂ 2 f ∂ X 2 X ^ f(X)=f(X_0)+\frac{\partial f^T}{\partial X}\hat{X}+\frac{1}{2}\hat{XT}\frac{\partial2 f}{\partial X^2}\hat{X} f(X)=f(X0)+∂X∂fTX+21XT∂X2∂2fX^
上式给出了特征点 X 0 X_0 X0附近函数的近似值 f ( x ) f(x) f(x),其中 X ^ = X − X 0 \hat{X}=X-X_0 X^=X−X0,对该式求取一阶导数零点,即可得函数实际极值点位置与 X 0 X_0 X0的距离,从而对离散特征点修正到亚尺度处。
f ′ ( X ) = ∂ f T ∂ X + ∂ f 2 ∂ X 2 X ^ f’(X)=\frac{\partial f^T}{\partial X}+\frac{\partial f^2}{\partial X^2}\hat{X} f′(X)=∂X∂fT+∂X2∂f2X^
X ^ e x = − ∂ 2 f − 1 ∂ X 2 ∂ f ∂ X \hat{X}{ex}=-\frac{\partial^2 f^{-1}}{\partial X^2}\frac{\partial f}{\partial X} X^ex=−∂X2∂2f−1∂X∂f
带入前式可求取新的特征点的灰度值:
f ( X ′ ) = f ( X 0 ) + 1 2 ∂ f T ∂ X ′ X ^ e x f(X’)=f(X_0)+\frac{1}{2}\frac{\partial f^T}{\partial X’}\hat{X}{ex} f(X′)=f(X0)+21∂X′∂fTX^ex
需要注意的是,上式是一个不断迭代的过程,也即根据当前特征点二阶泰勒求取新的特征点这一过程会不断重复直到满足终止条件,如 X ^ \hat{X} X^过小。另需注意当所得解超出离散极值点一定范围时需要舍去,因为二阶泰勒拟合只在其附近有效。
附:一个挺有意思的点在于这里的迭代目的和梯度下降法里的迭代并不是同一个目的,梯度下降里我们求取的是函数在某点的梯度,因为我们很难对复杂非线性的神经网络求除其一阶导数零点,即使求取到了也可能落入局部极值;而这里我们是直接求到了函数的一阶零点,迭代的目的是因为函数本身是一种近似,泰勒展开只取到了第二项,需要不断对原函数进行近似。这两种迭代的目的并不相同。
4.低对比度去除
目的和之间的阈值化类似,同样是去除掉没那么剧烈变化的特征点。要求:
∣ f ( x ) ∣ ≥ T n |f(x)|\geq\frac{T}{n} ∣f(x)∣≥nT
5.边缘效应去除
引言中提过我们想要提取的特征点为角点而非边缘,而前述一系列措施只能保证取到灰度值变换剧烈的点,而边缘点同样符合这一特征,因此我们将通过以下方式去除边缘点。
计算黑森矩阵 H ( x , y ) = [ D x x ( x , y ) D x y ( x , y ) D y x ( x , y ) D y y ( x , y ) ] H(x,y)=
[Dxx(x,y)Dyx(x,y)Dxy(x,y)Dyy(x,y)]H(x,y)=[Dxx(x,y)Dyx(x,y)Dxy(x,y)Dyy(x,y)]
若矩阵行列式 D e t ( H ) < 0 Det(H)<0 Det(H)<0,舍去该特征点
若矩阵行列式和迹不满足: T r ( H ) D e t ( H ) < ( γ 0 + 1 ) 2 γ 0 \frac{Tr(H)}{Det(H)}<\frac{(\gamma_0+1)^2}{\gamma_0} Det(H)Tr(H)<γ0(γ0+1)2,舍去该特征点, γ 0 \gamma_0 γ0为有实际意义的经验值,通常设定为10。
接下来解释以下这几个步骤的意义,角点和边缘点的区别在于边缘在图像中表现为一条线,垂直于线的方向频率高,沿着线的方向频率比较低;而角点则在多(大于2)个方向方向出现强高频分量。黑森矩阵实际上是函数的二阶偏导构成的矩阵,可以反应函数的曲率变化状况。又对于二次型矩阵有如下性质:
假定二次型矩阵 H H H两个特征值为 α , β \alpha,\beta α,β,则 D e t ( H ) = α β Det(H)=\alpha\beta Det(H)=αβ, T r ( H ) = α + β Tr(H)=\alpha+\beta Tr(H)=α+β;
实二次型矩阵的特征值异号时,该矩阵为不定矩阵,黑森矩阵为不定矩阵时,该临界点为非极值点;
黑森矩阵的特征值标定了函数在相应特征向量方向上变化的快慢。
由性质1,2我们可以推导处当 D e t ( H ) < 0 Det(H)<0 Det(H)<0时,特征点为非极值点,舍去;
由性质1,3我们可以推导出当 T r ( H ) D e t ( H ) = ( α + β ) 2 α 2 β 2 \frac{Tr(H)}{Det(H)}=\frac{(\alpha+\beta)2}{\alpha2\beta^2} Det(H)Tr(H)=α2β2(α+β)2过小时,由两特征特征向量的比值 γ \gamma γ构成的式子 ( γ + 1 ) 2 γ \frac{(\gamma+1)^2}{\gamma} γ(γ+1)2同样较小,且对勾函数在 γ > 1 \gamma>1 γ>1时单增,我们可以根据 T r ( H ) D e t ( H ) \frac{Tr(H)}{Det(H)} Det(H)Tr(H)大小判断特征向量的相对大小,该值过小,说明函数在该点不同方向上的变化非常不均匀,类似于边缘,舍去。
四、特征点描述子
通过前述步骤,我们已经获得了不同尺寸层面上的稳定特征点,接下来需要对其进行描述。
- 确定特征点区域方向
引言中提到为了使特征点拥有旋转不变性,我们会将特征点区域统一旋转到特定方向,这一方向即为特征点区域的主方向,因此我们需要先确定主方向。
计算方式为:统计在离该特征点尺度 σ ∗ \sigma^* σ∗最近的尺度层 σ o c t 上 , \sigma_{oct}上, σoct上,以特征点为中心 3 σ ′ = 3 ∗ 1.5 σ o c t 3\sigma’=31.5\sigma_{oct} 3σ′=3∗1.5σoct范围内的像素的梯度幅值及方向,对于范围内的梯度幅值用 1.5 σ ∗ 1.5\sigma^ 1.5σ∗高斯核滤波以实现距离加权。得到一系列梯度幅值和方向对 p a i r s = { a m p , a n g } pairs={amp,ang} pairs={amp,ang}后,将 360 ° 360° 360°方向划分为多个bins,将包含相应 a n g ang ang的 p a i r s pairs pairs中的 a m p amp amp值累加到对应的bins上,如果 a n g ang ang在两个bins划分间则根据距离分配 a m p amp amp。(此处和HOG算法类似,可自行查阅)。最终可以获得特征点区域内幅值-方向直方图,选取其中幅值最大的方向作为主方向。
在这里插入图片描述
附:这里的几个参数像是统计区域的半径,高斯加权的方差,有着不同的设置方式,但内在思路是一致的。此外如果在主方向之外出现了幅值达到了主方向幅值80%的其他方向,我们会将其作为辅方向,后续匹配时会出现两个位置、尺度相同但方向不同的两个特征点区域。
2. 特征点区域描述子
获得了特征点区域的主方向之后,我们就可以利用该值计算出有旋转不变性的描述子了。首先还是和前一步类似,统计该特征点所在尺度层面一定区域内的梯度幅值和方向,实施起来略有不同。
首先在特征点所处尺度层面内划定特征区域,半径为:
r = 3 2 σ o c t ( d + 1 ) 2 r=\frac{3\sqrt{2}\sigma_{oct}(d+1)}{2} r=232σoct(d+1),其中 d d d为我们在一个维度上划分的子块数目,通常为4;
将该区域划分为共 d ∗ d d*d d∗d个子块,每个子块内包含多个像素点 ;
将划定出来的区域旋转到该区域的主方向(前一步已求出);
在每个子块内构筑幅值-方向直方图,统计8个方向的梯度幅值。由此该区域可用 8 ∗ d ∗ d 8*d*d 8∗d∗d维向量表示,由此完成了特征点区域描述子的构建;在这里插入图片描述
附:需要注意的是以上的计算都是发生在相应的高斯金字塔尺度层面上,而非原图或者DOG上,此外由于旋转产生的像素值丢失通过插值算法解决,可以自行了解。如果想在原图上可视化SIFT特征,需要将我们获得的稳定特征点坐标变换回原始的图像尺寸上,简单的乘以原下采样倍数即可。
总结
至此SIFT算法就讲解完毕了,匹配的部分根据提的特征采用其他的聚类算法即可,总的来说这个算法还是有一定难度,本文也只是针对其他博客没有提到的细节引入了数学推导,使得整个思考过程更加连贯,更加详细的数学证明如有限差分法还请移步参考。
https://blog.csdn.net/Dr_maker/article/details/121442210
相关文章:

OpenCV-SIFT算法详解
系列文章目录 文章目录 系列文章目录引言一、高斯金字塔二、高斯差分金字塔三、特征点处理四、特征点描述子总结 引言 SIFT算法是为了解决图片的匹配问题,想要从图像中提取一种对图像的大小和旋转变化保持鲁棒的特征,从而实现匹配。这一算法的灵感也十分…...

Java中的接口到底是什么?
要说Java的【接口】,可以将其类比为现实生活中的一种约定或规范。在Java中,接口定义了一组方法的集合,但没有提供这些方法的具体实现。 你可以将接口看作是一个合同,它规定了一个类必须实现的一组方法。这些方法描述了类所需具备…...
Jpa与Druid线程池及Spring Boot整合(一): spring-boot-starter-data-jpa 搭建持久层
Jpa与Druid线程池及Spring Boot整合(一) Jpa与Druid线程池及Spring Boot整合(二):几个坑 附录官网文档:core.domain-events域事件 (一)Jpa与Druid连接池及Spring Boot整合作为持久层,遇到系列问题,下面一 一记录: pom.xml 文件中加入必须的…...
helm部署vmalert
先决条件 安装以下软件包:git, kubectl, helm, helm-docs,请参阅本教程。 在 CentOS 上启用 snap 并安装 helm 启用 snapd 使用以下命令将 EPEL 存储库添加到您的系统中: sudo yum install epel-release 按如下方式安装 Snap࿱…...

加工厂数字孪生3D可视化展示系统重塑管理模式
近年来“数字化转型”成立各行业聚焦的发展方向,在工业制造领域,智慧工业数字孪生可视化平台作为一种新型的技术手段,或将成为助力企业跑赢数字化转型最后一公里。 提高生产效率 传统的生产方式往往需要大量的人工干预,不仅耗时耗…...

php从静态资源到动态内容
1、从HTML到PHP demo.php:后缀由html直接改为php,实际上当前页面已经变成了动态的php应用程序脚本 demo.php: 允许通过<?php ... ?>标签,添加php代码到当前脚本中 php标签内部代码由php.exe解释, php标签之外的代码原样输出,仍由web服务器解析 <!DOCTYPE html>…...

JavaScript:模块化【CommonJS与ES6】
在 JavaScript 编程中,随着项目的复杂性增加,代码的组织和管理变得至关重要。模块化是一种强大的编程概念,它允许我们将代码划分为独立的模块,提高了可维护性和可扩展性。本文将详细介绍 CommonJS 和 ES6 模块,帮助你理…...
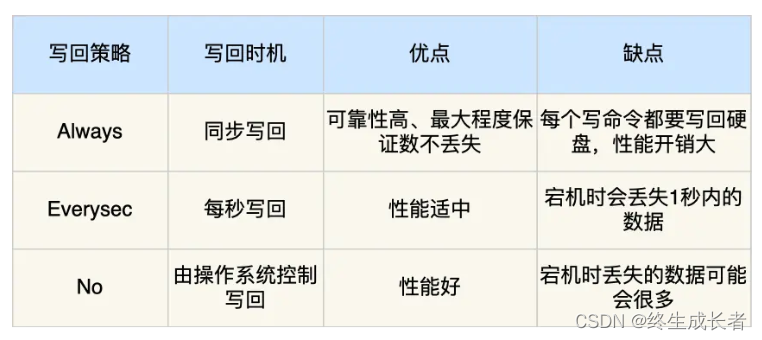
Redis—持久化
这里写目录标题 AOF三种写回策略写回策略的优缺点AOF 重写机制AOF后台重写AOF优缺点使用命令 RDBRDB 持久化的工作原理执行快照时,数据能被修改吗RDB 持久化的优点RDB 持久化的缺点 混合持久化大key对持久化的影响 AOF 保存写操作命令到日志的持久化方式࿰…...
【设计模式】代理模式
在代理模式(Proxy Pattern)中,一个类代表另一个类的功能。这种类型的设计模式属于结构型模式。 在代理模式中,我们创建具有现有对象的对象,以便向外界提供功能接口。 介绍 意图:为其他对象提供一种代理以…...

mac arm 通过brew搭建 php+nginx+mysql+xdebug
1.安装nginx brew install nginx //安装brew services start nginx //启动2.安装php brew install php7.4 //安装export PATH"/opt/homebrew/opt/php7.4/bin:$PATH" //加入环境变量 export PATH"/opt/homebrew/opt/php7.4/sbin:$PATH"brew serv…...

软信天成:告别手动编码,实现智能自动化云数据管理
数字化转型浪潮之下,各个企业都在大力投资新的基于云的流程、平台和环境,以期获取可扩展性、弹性、敏捷性和成本效益等优势。 这些趋势要求企业IT部门能够帮助组织,在对分析进行现代化改造的过程中达到云就绪或云优先状态。事实上࿰…...
易基因:ChIP-seq等揭示转录因子NRF1调控原始生殖细胞发育、增殖和存活的表观遗传机制|科研进展
大家好,这里是专注表观组学十余年,领跑多组学科研服务的易基因。 原始生殖细胞(Primordial germ cell,PGC)是生殖细胞前体,可以产生卵母细胞和精子,确保生命延续。尽管PGC特化(PGC …...

35岁,体能断崖?你需要健康的生活习惯
大厂裁员,称35岁以后体能下滑,无法继续高效率地完成工作;体重上涨,因为35岁以后新陈代谢开始变慢;甚至坐久了会腰疼、睡眠困扰开始加重,在众多的归因中,35岁的到来,为一切的焦虑埋下…...

mysql 习题总结
1.select sex,avg(salsry) as 平均薪资 from emp group by sex; 2.select depart,sum(salsry) from emp group by depart; 3.select depart ,sum(salary) from emp group by depart order by sum(salary) desc limit 1,1; 4.select name from emp group by name having count(n…...

IL汇编语言做一个窗体
网上看到一段代码, .assembly extern mscorlib {} .assembly Classes { .ver 1:0:1:0 } .namespace MyForm { .class public TestForm extends [System.Windows.Forms]System.Windows.Forms.Form { .field private class [System]…...
不用技术代码,分班查询系统怎么做?
暑假即将结束,新学期开始将面临分班信息公布的工作!对于分班信息公布,涉及到学生的个人信息,包括姓名、学号、班级等。在发布这些信息时,必须确保数据的保密性,防止未经授权的人员获取到学生的个人信息。因…...

【Mybatis】调试查看执行的 SQL 语句
1. 问题场景: 记录日常开发过程中 Mybatis 调试 SQL 语句,想要查看Mybatis 中执行的 SQL语句,导致定位问题困难 2. 解决方式 双击shift找到mybatis源码中的 MappedStatement的getBoundSql()方法 public BoundSql getBoundSql(Object para…...
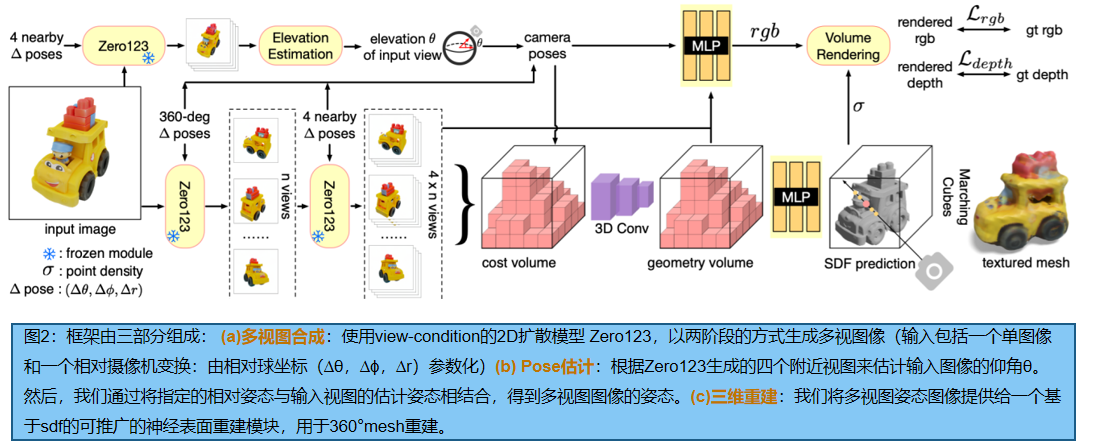
【多视重建】从Zero-123到One-2-3-45:多视角生成
文章目录 摘要一、引言二、相关工作三、Zero-1-to-33.1.学习如何控制照相机的视角3.2.视角作为条件的扩散3.3三维重构3.4 数据集 四、One-2-3-454.1 Zero123: 视角条件的 2D Diffusion4.2 NeRF优化:将多视图预测提升到三维图像4.3 基于不完美多视图的 神经表面重建*…...
Unity开发Vision Pro——参考文档)
(四)Unity开发Vision Pro——参考文档
4.参考文档 4.1 支持的功能和组件 4.1.1 支持的 Unity 功能和组件 大多数 Unity 组件无需修改即可在此平台上运行 - 包括大多数自定义 MonoBehaviours、动画逻辑、物理、输入处理、资产管理、AI 等。然而,需要渲染的组件需要特殊的支持。因此,一些组件…...
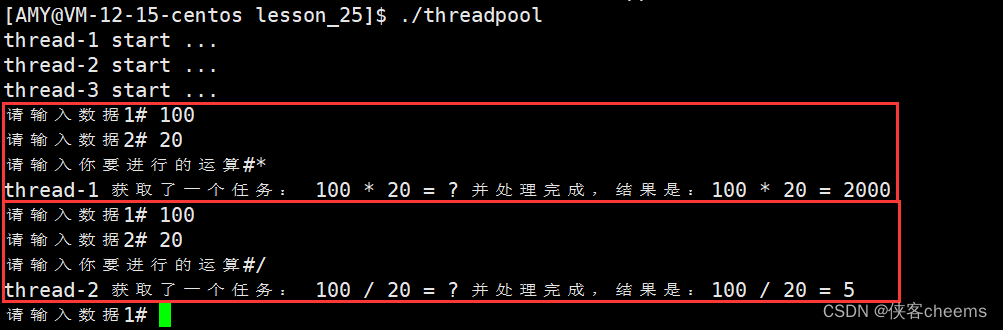
【Linux】简单线程池的设计与实现 -- 单例模式
前言对锁的封装整体代码LockGuard - RALLRALLMutex封装 对线程创建的封装整体代码成员函数解释声明 业务处理封装-加减乘除(可有可无)整体代码成员函数解释声明 线程池的设计与实现整体代码成员函数解释声明 展示 前言 线程池: 一种线程使用模式。线程过…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...
