卫星--夏令营
几何问题:就是用几何数学知识解题即可
但是越是数学+编程题,越容易忽略数学题中的细节
1.地球![]() 半径你算进去了吗?
半径你算进去了吗?
2.sin三角函数,M_PI标准圆周率在cmath文件里
3.有可能给出的夹角超过180°呢,没给数据要求,就要自己考虑到
#include <iostream>
#include<cmath>
#include<cstdio>
using namespace std;const int r = 6440;int main()
{double s, a;char f[4];while (cin >> s >> a >> f){if (f[0] == 'm') a /= 60;a = a * M_PI / 180;double zz = a * (s + r);double rr = 2 * (s + r) * sin(a / 2);if (a > M_PI) zz = 2 * (s + r) * M_PI - zz;printf("%.6lf %.6lf\n", zz,rr);}return 0;
}
相关文章:

卫星--夏令营
几何问题:就是用几何数学知识解题即可 但是越是数学编程题,越容易忽略数学题中的细节 1.地球半径你算进去了吗? 2.sin三角函数,M_PI标准圆周率在cmath文件里 3.有可能给出的夹角超过180呢,没给数据要求,就要自己考…...
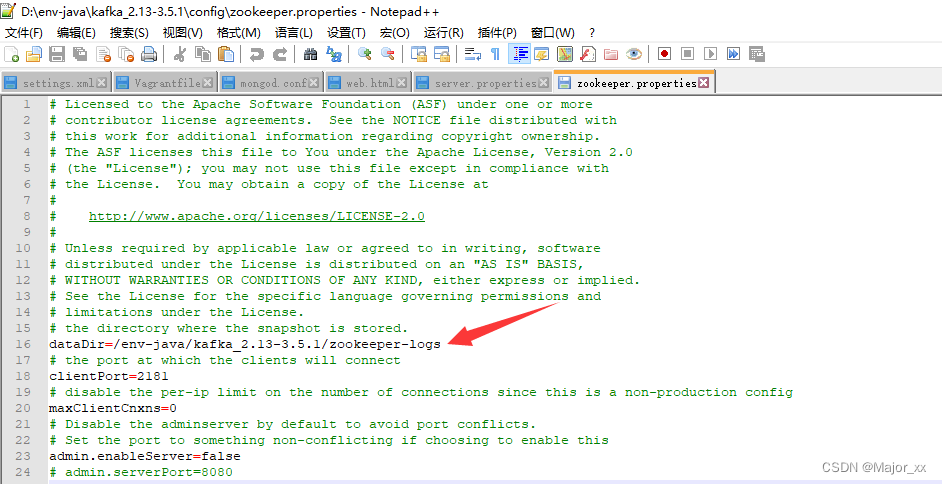
Kafka的下载安装以及使用
一、Kafka下载 下载地址:https://kafka.apache.org/downloads 二、Kafka安装 因为选择下载的是 .zip 文件,直接跳过安装,一步到位。 选择在任一磁盘创建空文件夹(不要使用中文路径),解压之后把文件夹内容…...
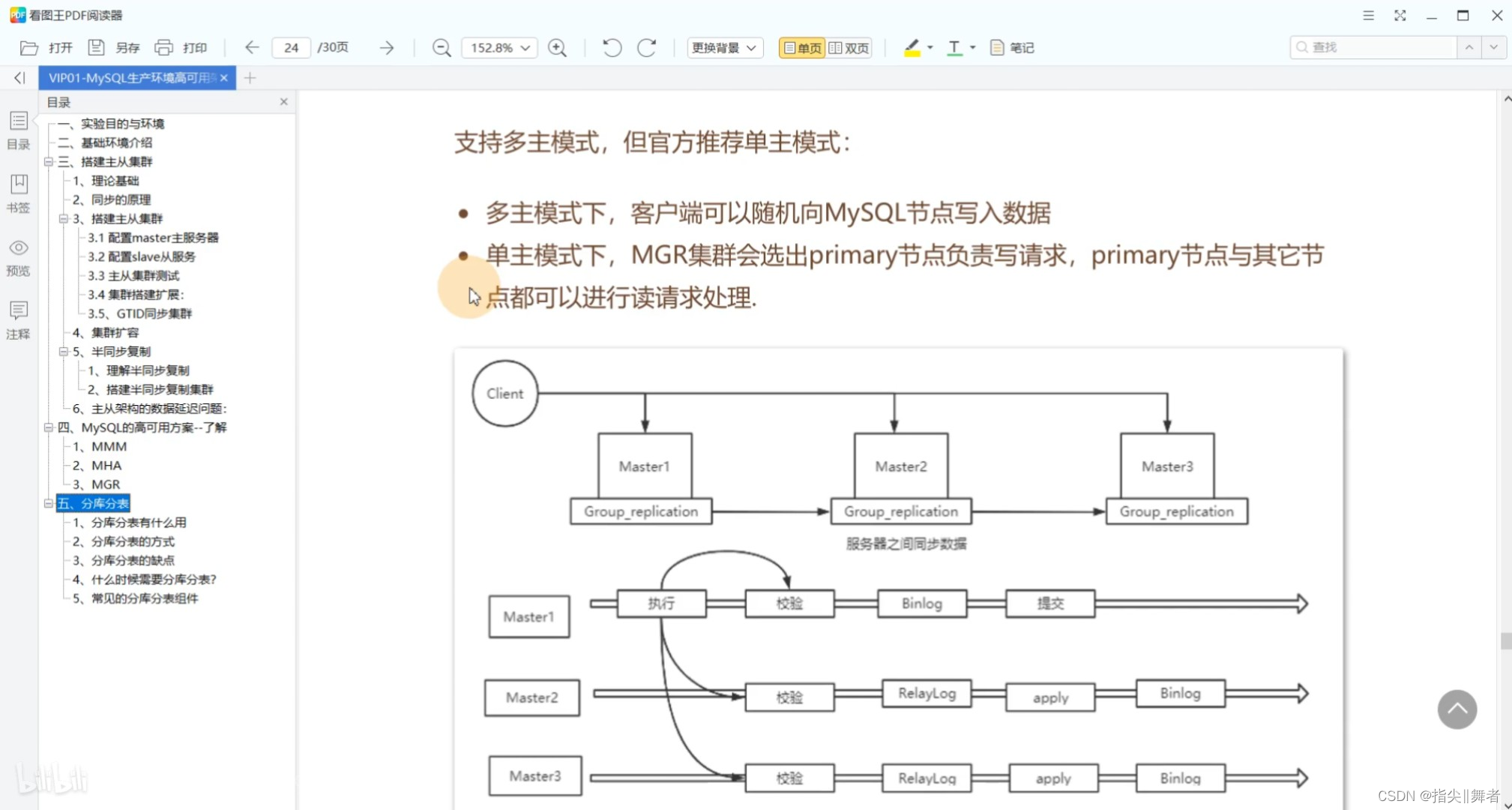
数据库相关面试题
巩固基础,砥砺前行 。 只有不断重复,才能做到超越自己。 能坚持把简单的事情做到极致,也是不容易的。 mysql怎么优化 : MySQL的优化可以从以下几个方面入手: 数据库设计优化:合理设计表结构,选择合适的数…...
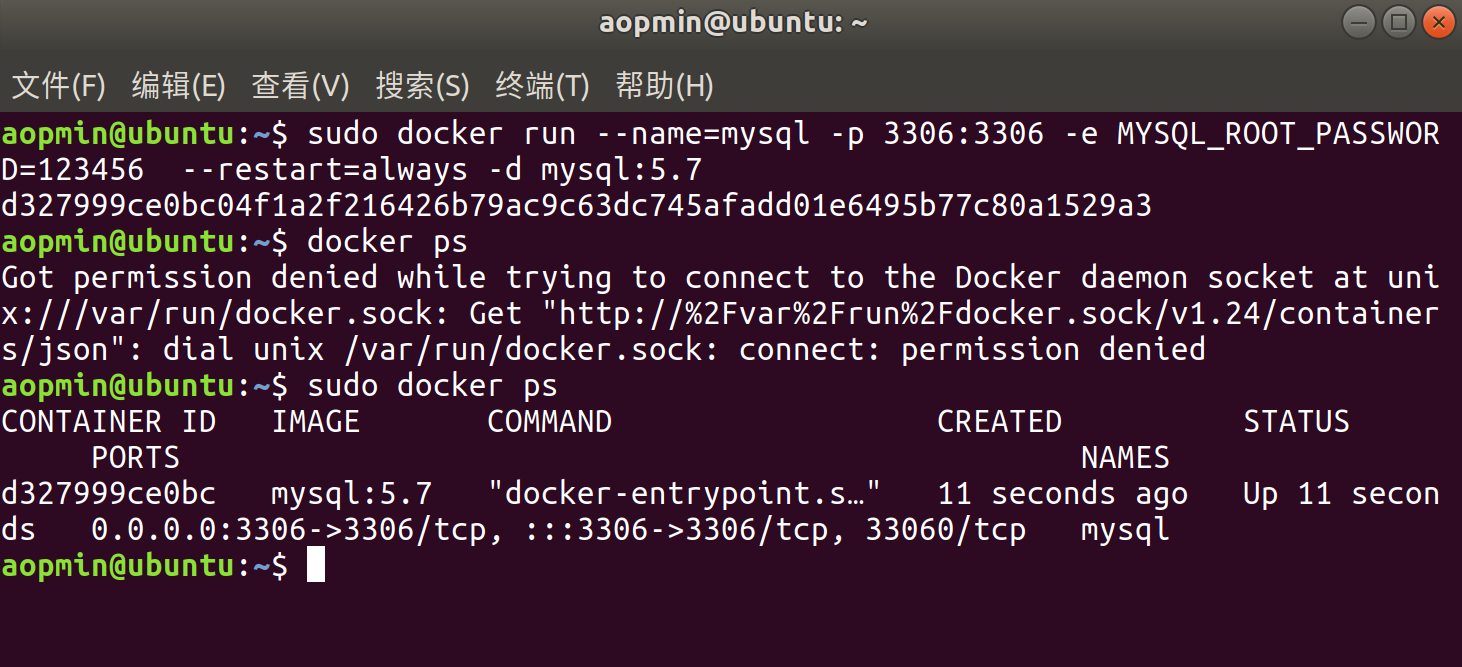
Ubuntu常用配置
文章目录 1. 安装VMware虚拟机软件2. 下载Ubuntu镜像3. 创建Ubuntu虚拟机4. 设置屏幕分辨率5. 更改系统语言为中文6. 切换中文输入法7. 修改系统时间8. 修改锁屏时间9. 通过系统自带的应用商店安装软件10. 安装JDK11. 安装 IntelliJ IDEA12. 将左侧任务栏自动隐藏13. 安装docke…...

win10MySQLServer安装过程+解决MySQL服务无法启动问题
本次使用的版本是 Server version: 8.0.33 MySQL Community Server 安装详解 首先去官网下载社区版,比如我用的是mysql-8.0.33-winx64.zip,解压到文件夹:D:\Program Files\mysql-8.0.33-winx64 用管理员身份运行cmd,进到bin目录…...
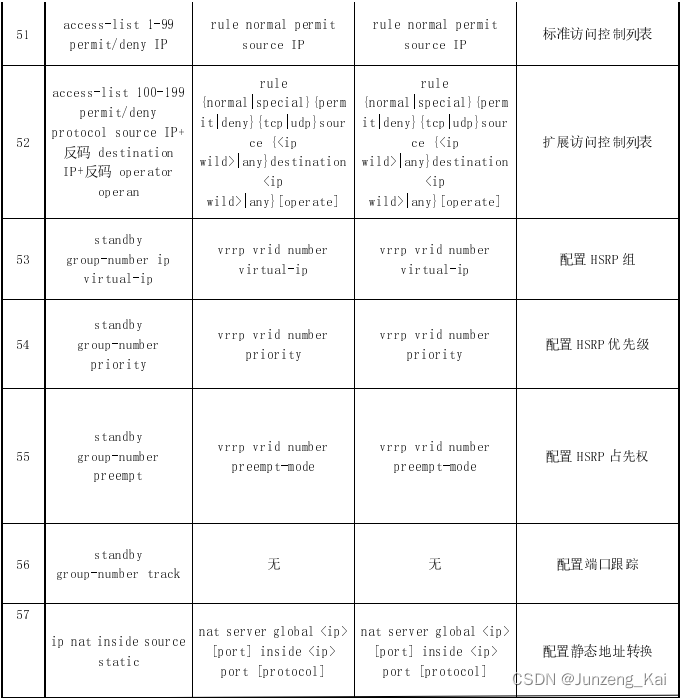
网络:CISCO、Huawei、H3C命令对照
思科、华为、锐捷命令对照表 编号思科华为锐捷命令解释1 2writesavesave保存3456 如果你所处的视图为非系统视图,需要查看配置的时候,需要在该配置命令前加do。 在特定的视图之下,有对应的特定命令。例如,在接口视图下的ip addre…...

题目:2319.判断矩阵是否是 X 矩阵
题目来源: leetcode题目,网址:2319. 判断矩阵是否是一个 X 矩阵 - 力扣(LeetCode) 解题思路: 遍历矩阵,对于每一个节点,先判断是否处于主对角线或副对角线上,然后判…...

2023年大厂前端面试题汇总
一、58同城前端面试题27道 1. css盒模型 2. css画三角形 3. 盒子水平垂直居中(所有方式) 4. 重绘、重排 重绘就是重新绘制(repaint):是在一个元素的外观被改变所触发的浏览器行为,浏览器会根据元素的新属性…...

如何在Linux中查找Nginx安装目录
一、通过which命令查找 $ which nginx /usr/sbin/nginxwhich命令会在系统环境变量PATH中查找nginx可执行文件,并返回路径。因此,通过which命令可以很容易地找到系统中nginx的安装位置。 二、通过whereis命令查找 $ whereis nginx nginx: /usr/sbin/ng…...

【NLP】训练LLM的不同方式
一、说明 在大型语言模型(LLM)领域,有各种各样的 训练机制,具有不同的手段,要求和目标。由于它们服务于不同的目的,因此重要的是不要将它们相互混淆,并了解它们适用的不同场景。 在本文中&#…...
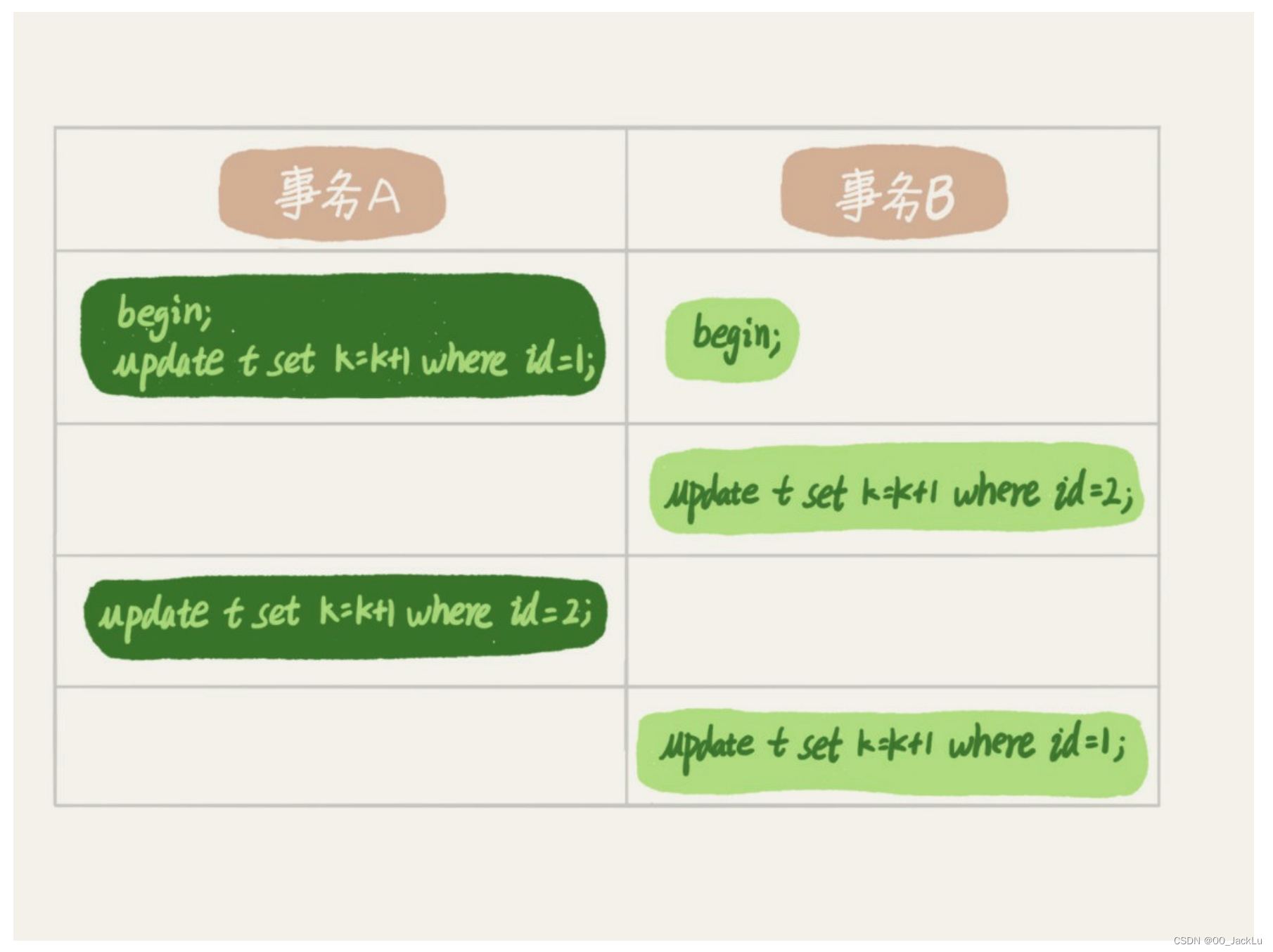
MySQL 45讲笔记(1-10讲)
1. SQL语句如何开始执行? MySQL分为Server和存储引擎两部分: Server层包含连接器、存储缓存、分析器、执行器等,以及所有的内置函数(事件、日期)等等,还有视图、触发器。 存储引擎是负责数据的存储和提取&a…...
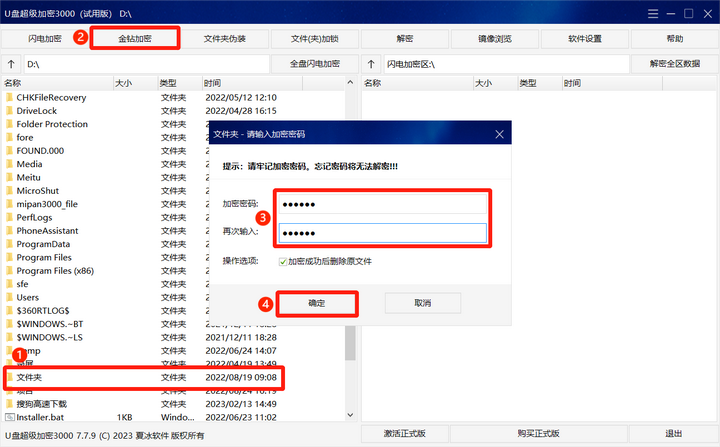
U盘数据如何保密?U盘数据加密软件合集
当我们将重要数据存放在U盘中时,必须要保障U盘的安全,以避免数据泄露。那么,U盘数据该如何保密呢?下面我们就来盘点一下那些好用的U盘数据保护方法。 U盘写保护 起初U盘写保护是专门为U盘防病毒而设计的,写保护后会将…...
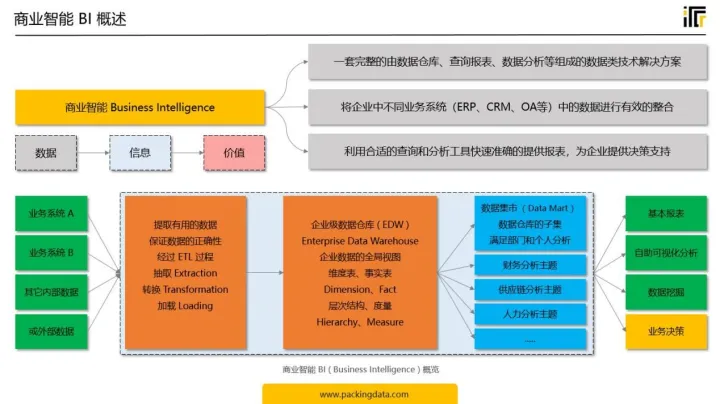
此文详解,数据仓库管理建设的经验
目前由于数据分散在不同的存储环境或数据库中,对于新业务需求的开发需要人工先从不同的数据库中同步、集中、合并等处理,造成资源和人力的浪费。同时,目前的系统架构,无法为未来数据驱动业务创新的理念提供友好的支撑。需要建设新…...
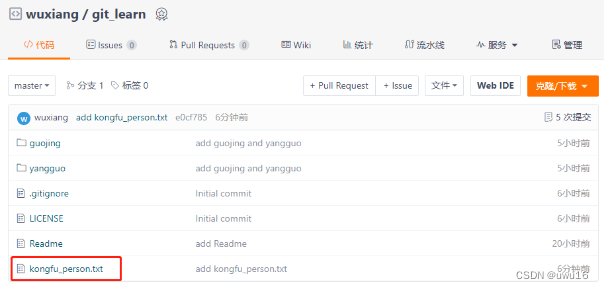
01 - 工作区、暂存区、版本库、远程仓库 - 以一次连贯的提交操作为例
查看所有文章链接:(更新中)GIT常用场景- 目录 文章目录 1. 工作区、暂存区、版本库、远程仓库1.1 工作区1.2 工作区 > 暂存区:git add1.3 暂存区 > 版本库:git commit1.4 push到远程仓库 1. 工作区、暂存区、版本…...

cesium学习记录06-视图、场景与相机
一、视图(Viewer) viewer是cesium的核心类,是一切的开端。通过new Cesium.Viewer(container, options)来创建一个Viewer对象,而通过这个 Viewer对象,可以添加图层、实体、相机控制等,以及设置一些全局属性…...

flutter开发实战-MethodChannel实现flutter与原生Android双向通信
flutter开发实战-MethodChannel实现flutter与原生Android双向通信 最近开发中需要原生Android与flutter实现通信,这里使用的MethodChannel 一、MethodChannel MethodChannel:用于传递方法调用(method invocation)。 通道的客户端和宿主端通过传递给通…...
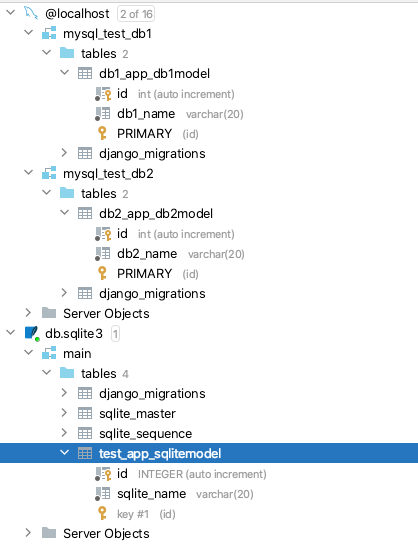
django使用多个数据库实现
一、说明: 在开发 Django 项目的时候,很多时候都是使用一个数据库,即 settings 中只有 default 数据库,但是有一些项目确实也需要使用多个数据库,这样的项目,在数据库配置和使用的时候,就比较麻…...

Linux常见面试题,应对面试分享
操作系统基础 1.cpu占⽤率太⾼了怎么办? 排查思路是什么,怎么定位这个问题,处理流程 其他程序: 1.通过top命令按照CPU使⽤率排序找出占⽤资源最⾼的进程 2.lsof查看这个进程在使⽤什么⽂件或者有哪些线程 3.询问开发或者⽼⼤,是什么业务在使⽤这个进程…...
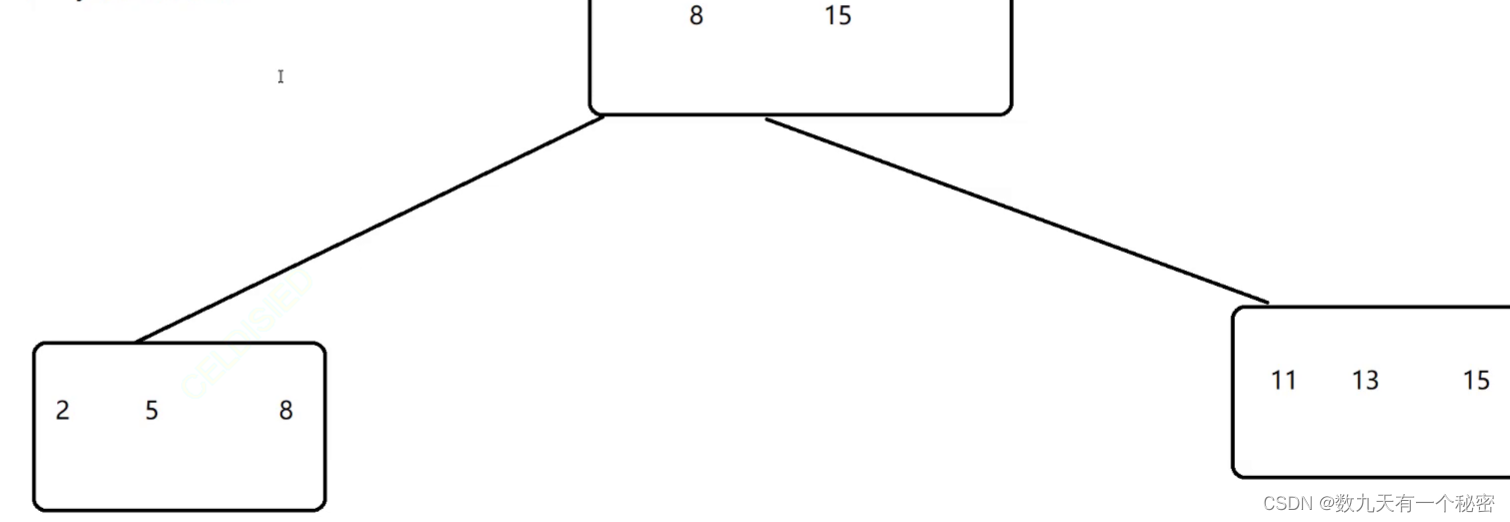
mysql索引的数据结构(Innodb)
首选要注意,这里的数据结构是存储在硬盘上的数据结构,不是内存中的数据结构,要重点考虑io次数. 一.不适合的数据结构: 1.Hash:不适合进行范围查询和模糊匹配查询.(有些数据库索引会使用Hash,但是只能精准匹配) 2.红黑树:可以范围查询和模糊匹配,但是和硬盘io次数比较多. 二…...

【MySQL】Java实现JDBC编程
文章目录 1. JDBC2. 添加驱动包3. 编程3.1 创建数据源3.2 与数据库建立连接3.3 构造SQL语句3.4 执行SQL语句3.5 释放资源,关闭连接 1. JDBC 数据库编程必须掌握至少一门编程语言,一种数据库,会导入数据库驱动包。 操作和连接不同数据库都需要…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...
