休息是不可能休息的
654.最大二叉树
分析:相比较遍历顺序构建二叉树,这个相对简单。
思路:每次找到数组最大值,然后分割数组
class Solution {
public:TreeNode*judge(vector<int>&nums){if(nums.size()==0) return nullptr;int maxNum=0,index=0;for(int i=0;i<nums.size();i++){//获取最大值和下标if(nums[i]>maxNum){maxNum=nums[i];index=i;}}TreeNode*root=new TreeNode(maxNum);if(nums.size()==1) return root;//切割左子树和右子树vector<int> leftNums(nums.begin(),nums.begin()+index);vector<int> rightNums(nums.begin()+index+1,nums.end());root->left=judge(leftNums);root->right=judge(rightNums);return root;}TreeNode* constructMaximumBinaryTree(vector<int>& nums) {//思路:每次找到数组中最大值,然后进行左右切割return judge(nums);}
};617.合并二叉树
思路一:创建一个新的二叉树,每次同时传入二叉树的同一位置
class Solution {
public:TreeNode* judge(TreeNode*root1,TreeNode*root2){if(root1==nullptr && root2==nullptr) return nullptr;TreeNode*newNode=new TreeNode();if(root1!=nullptr && root2!=nullptr){newNode->val=root1->val+root2->val;newNode->left=judge(root1->left,root2->left);newNode->right=judge(root1->right,root2->right);} if(root1==nullptr && root2!=nullptr){newNode->val=root2->val;newNode->left=judge(nullptr,root2->left);newNode->right=judge(nullptr,root2->right);} if(root1!=nullptr && root2==nullptr){newNode->val=root1->val;newNode->left=judge(root1->left,nullptr);newNode->right=judge(root1->right,nullptr);} return newNode;}TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {//思路:直接同时遍历两个二叉树,子节点不存在传入下一个为空指针if(root1==nullptr) return root2;if(root2==nullptr) return root1;if(root1==nullptr && root2==nullptr) return nullptr;return judge(root1,root2);}
};思路二:以其中一棵二叉树作为返回值,尽量不创建节点
class Solution {
public:TreeNode* judge(TreeNode*root1,TreeNode*root2){if(root1==nullptr && root2==nullptr) return nullptr;if(root1!=nullptr && root2!=nullptr){root1->val+=root2->val;root1->left=judge(root1->left,root2->left);root1->right=judge(root1->right,root2->right);} else if(root1==nullptr && root2!=nullptr){TreeNode*newNode=new TreeNode();newNode->val=root2->val;newNode->left=judge(nullptr,root2->left);newNode->right=judge(nullptr,root2->right);return newNode;} return root1;}TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {//思路:直接同时遍历两个二叉树,子节点不存在传入下一个为空指针if(root1==nullptr) return root2;if(root2==nullptr) return root1;if(root1==nullptr && root2==nullptr) return nullptr;root1->val+=root2->val;root1->left=judge(root1->left,root2->left);root1->right=judge(root1->right,root2->right);return root1;}
};700.二叉搜索树中的搜索
思路:判断大小,搜索
class Solution {
public:TreeNode* searchBST(TreeNode* root, int val) {//思路:找到节点,然后返回//分析:左子节点比父节点小,右子节点比父节点大if(root==nullptr)return root;TreeNode*newNode=root;;if(newNode->val>val)newNode=searchBST(newNode->left,val);else if(newNode->val<val)newNode=searchBST(newNode->right,val);return newNode;}
};98.验证二叉搜素树
思考:从二叉搜索树的特性入手,二叉搜索树的中序遍历必然是递增序列
分析:细节方面很要注意
class Solution {
public:vector<int>ans;void judge(TreeNode*root){if(root==nullptr) return;judge(root->left);ans.push_back(root->val);judge(root->right);}bool isValidBST(TreeNode* root) {//思路:直接分析//思路二:中序遍历的数组一定递增judge(root);if(ans.size()==1) return true;int pre=ans[0];for(int i=1;i<ans.size();i++){if(ans[i]<=pre)return false;pre=ans[i];}return true;}
};530.二叉搜索树的最小绝对差
思路:把所有节点加入数组,排序后两两计算最小差值
class Solution {
public:vector<int>ans;void judge(TreeNode*root){if(root==nullptr) return;ans.push_back(root->val);judge(root->left);judge(root->right);}int getMinimumDifference(TreeNode* root) {//思路:把父节点的值传入子节点,然后更新最小差值//问题:题目要求是任意节点,所以考虑先加入数组,排序后两两计算judge(root);sort(ans.begin(),ans.end());int minSub=INT_MAX;for(int i=1;i<ans.size();i++){int mid=abs(ans[i-1]-ans[i]);minSub=min(minSub,mid);}return minSub;}
};501.二叉搜索树中的众数
分析:众数就是出现多次的数
思路:使用哈希表,递归遍历所有节点
class Solution {
public:vector<int>res;unordered_map<int,int>map;void judge(TreeNode*root){if(root==nullptr)return;map[root->val]++;//记录出现的次数judge(root->left);judge(root->right);}vector<int> findMode(TreeNode* root) {judge(root);int maxNum=0;for(auto it:map){//第一次遍历获取出现最大频率if(it.second>maxNum) maxNum=it.second;}for(auto it:map){//找到众数if(it.second==maxNum) res.push_back(it.first);}return res;}
};236.二叉树的最近公共树祖先
思路一:通过左0右1获取两个节点的遍历路径,然后截取两个节点相同的遍历路径,使用相同的遍历路径直接获得最近公共树祖先
class Solution {
public:string midP="",midQ="";void judge(TreeNode*root,string judgeDist,TreeNode*p,TreeNode*q,string midP1,string midQ1){if(root==nullptr) return;midP1+=judgeDist;midQ1+=judgeDist;if(root==p) midP=midP1;if(root==q) midQ=midQ1;judge(root->left,"0",p,q,midP1,midQ1);judge(root->right,"1",p,q,midP1,midQ1); }TreeNode*search(TreeNode*root,queue<char> mid,int start){TreeNode*cur;if(mid.size()==0)return root;//分两种情况if(mid.front()=='1'){mid.pop();cur=search(root->right,mid,start+1);} else{mid.pop();cur=search(root->left,mid,start+1);} return cur;}TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {//思路:遍历二叉树,给左右子节点分别编号,找到两个节点之后匹配编号的相同位数,//然后用相同位数走到的那个节点就是最近公共祖先int i;queue<char>que;judge(root,"",p,q,"","");//cout<<midP.size()<<midQ.size();for(i=0;i<midP.size();i++){if(midP[i]!=midQ[i]) break;elseque.push(midP[i]);}//cout<<1;if(i==0) return root;string mid=midP.substr(0,i);cout<<mid.size()<<endl;return search(root,que,0);}
};235.二叉搜索树的最近公共祖先
思路一:比较出节点值大小,然后从根节点开始判断两个节点的位置
class Solution {
public:TreeNode* judge(TreeNode*root,TreeNode*first,TreeNode*second){//祖先节点在当前root上或者两个节点在当前root的两边if((first->val<=root->val && second->val>root->val) || (first->val<root->val && second->val>=root->val)) return root;TreeNode*res;//当前两个节点在同一边if(first->val<root->val && second->val<root->val)res=judge(root->left,first,second);else if(first->val>root->val && second->val>root->val)res=judge(root->right,first,second);return res;}TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {//思路:找到一个在两个节点中间的节点,或者等于较小值//比较出最小值if(p->val>q->val) return judge(root,q,p);return judge(root,p,q);}
};701.二叉搜索树的插入操作
思路一:直接遍历插入
class Solution {
public:void judge(TreeNode*root,int val){if(root->val>val){//需要插入左边if(root->left) judge(root->left,val);else{TreeNode*newNode=new TreeNode(val);root->left=newNode;}}else{//需要插入右边if(root->right) judge(root->right,val);else{TreeNode*newNode=new TreeNode(val);root->right=newNode;}}}TreeNode* insertIntoBST(TreeNode* root, int val) {if(root==nullptr){//考虑没有节点的情况return new TreeNode(val);}judge(root,val);return root;}
};450.删除二叉搜索树的节点
分析:这题做的好复杂,感觉饶了很多弯子,100多行居然还超过了68%哈哈哈哈哈
思路一:
1.考虑特殊情况,根节点不存在和要删除根节点。
2.考虑二叉树中没有要删除的节点。
3.递归遍历寻找left,或者right是否为要删除的节点,当找到时,将root和要删除的子节点传入res删除函数,其中变量judgeB判断是左子节点还是右子节点。
4.在删除节点时,需要判断该节点是否有左右子节点,都有的情况下需要使用add函数,将要删除的节点的左子节点放到右子节点的下面。使用add递归添加
class Solution {
public:bool judgeA=false;void add(TreeNode*root,TreeNode*node){//用于删除节点时,组合该节点的两个子节点if(node==nullptr) return;if(root->val>node->val){//插入节点在左边if(root->left)add(root->left,node);elseroot->left=node;}else{//插入节点在右边if(root->right)add(root->right,node);elseroot->right=node;}}void res(TreeNode*root,TreeNode*node, bool judgeB){//用于删除节点if(judgeB)//左子节点{if(node->left==nullptr && node->right==nullptr){//key值节点为叶子节点root->left=nullptr;return;}else if(node->left && node->right){//key值节点有左右节点root->left=node->right;add(node->right,node->left);return;}else if(node->left && !node->right)root->left=node->left;elseroot->left=node->right;}else{if(node->left==nullptr && node->right==nullptr){//key值节点为叶子节点root->right=nullptr;return;}else if(node->left && node->right){//key值节点有左右节点root->right=node->right;add(node->right,node->left);return;}else if(node->left && !node->right)root->right=node->left;elseroot->right=node->right;}}void judge(TreeNode*root,int key){//用于查找删除节点if(root==nullptr)return;if(root->val>key){//当父节点大于key,说明key在左边if(root->left->val==key){//当左子节点等于key时res(root,root->left,true);}elsejudge(root->left,key);}else if(root->val<key){if(root->right->val==key){res(root,root->right,false);}elsejudge(root->right,key);}}void judgeMax(TreeNode*root,int key){//用于判断二叉树中是否存在目标节点if(root==nullptr) return;if(root->val==key) judgeA=true;if(root->val>key) judgeMax(root->left,key);if(root->val<key) judgeMax(root->right,key);}TreeNode* deleteNode(TreeNode* root, int key) {//思路:遍历二叉树,找到节点时,判断当前节点左右两边情况//if(root==nullptr) return root;if(root->val==key){if(root->left && root->right){add(root->right,root->left);return root->right;}else if(root->left) return root->left;else if(root->right) return root->right;elsereturn nullptr;}judgeMax(root,key);if(judgeA==false){cout<<123;return root;} judge(root,key);return root;}
};相关文章:

休息是不可能休息的
654.最大二叉树 分析:相比较遍历顺序构建二叉树,这个相对简单。 思路:每次找到数组最大值,然后分割数组 class Solution { public:TreeNode*judge(vector<int>&nums){if(nums.size()0) return nullptr;int maxNum0,in…...

Java面向对象(内部类)(枚举)(泛型)
内部类 内部类是五大成员之一(成员变量、方法、构造方法、代码块、内部类); 一个类定义在另一个类的内部,就叫做内部类; 当一个类的内部,包含一个完整的事物,且这个事务不必单独设计…...

macOS - 安装 GNU make、cmake
文章目录 关于 cmake使用 brew 安装 关于 GNU make方式一:brew方式二:下载源码 关于 cmake 官网:https://cmake.org/ 使用 brew 安装 brew 安装 cmake: https://formulae.brew.sh/formula/cmake安装使用 brew : https://blog.csdn.net/lovec…...

vue中style scoped属性的作用
一、为什么要给style 节点加 scoped 属性(vue) 1、作用:当style标签里面有scoped属性时,它的css只作用于当前组建的元素。在单页面项目中可以使组件之间互不污染,实现模块化(实现组件的私有化,不…...

【ARM 嵌入式 编译系列 10.2 -- 符号表与可执行程序分离详细讲解】
文章目录 符号表与可执行程序分离方法一 使用eu-strip方法二 使用 objcopy上篇文章:ARM 嵌入式 编译系列 10.1 – GCC 编译缩减可执行文件 elf 文件大小 下篇文章:ARM 嵌入式 编译系列 10.3 – GNU elfutils 工具小结 符号表与可执行程序分离 接着上篇文章 ARM 嵌入式 编译…...

Gin各种参数接收
Gin参数接收 文章目录 Gin参数接收1.各个参数的接收方法Gin中发送JSON数据Gin接收querystring数据Gin接收Form的参数Gin接收URI参数 2.参数绑定方式接收(更加方便)推荐一款软件 1.各个参数的接收方法 声明: 这里的c都是c *gin.Context中的c Gin中发送JSON数据 在传输或接受JS…...
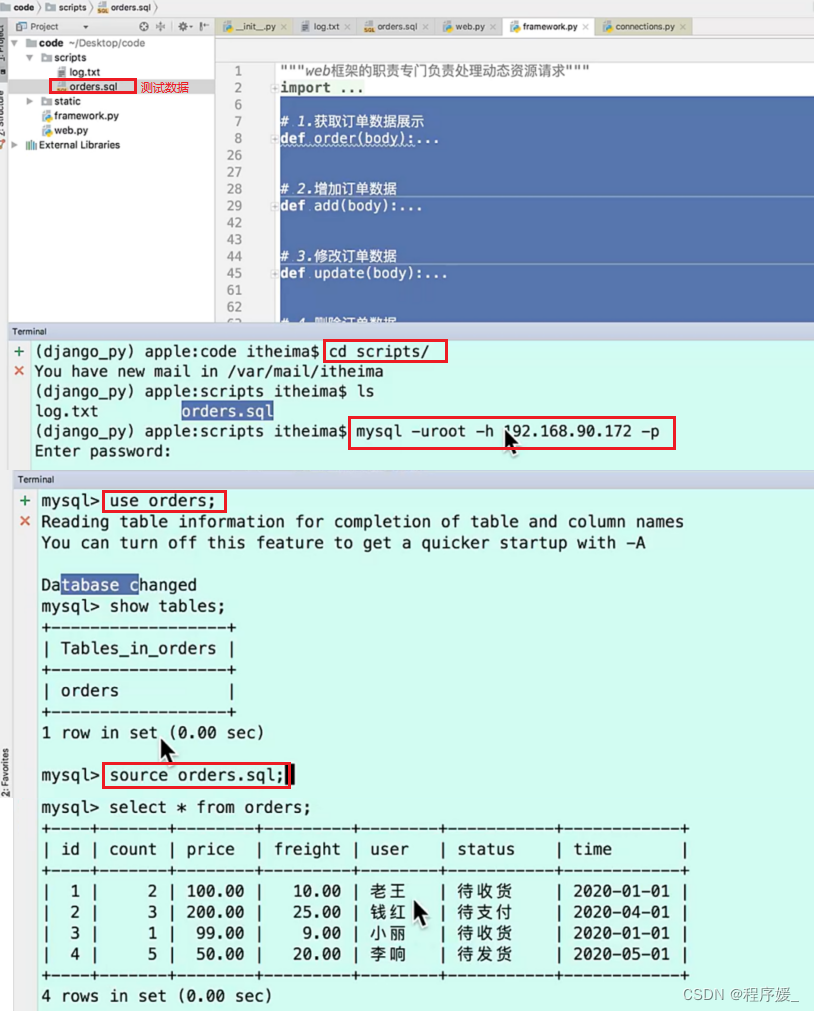
【Python】进阶之 MySQL入门教程
文章目录 数据库概述Mysql概述Mysql安装与使用Navicat安装和使用Mysql终端指令操作Mysql和python交互订单管理案例实现 数据库概述 数据库的由来 发展历程说明人工管理阶段用纸带等进行数据的存储文件系统阶段数据存储在文件中数据库阶段解决了文件系统问题高级数据库阶段分布式…...
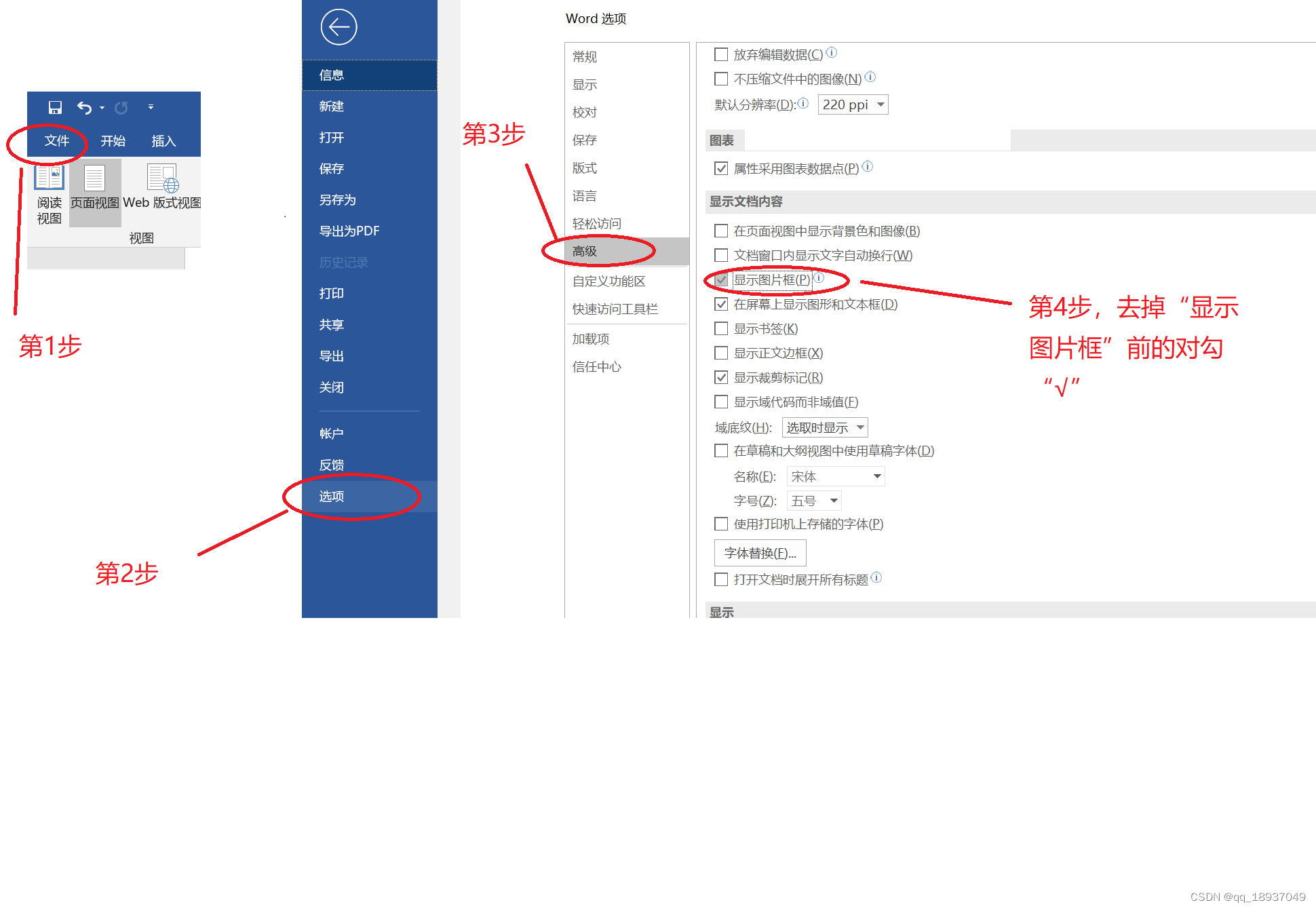
Word 2019打开.doc文档后图片和公式不显示(呈现为白框)的解决办法
Word 2019打开.doc文档后图片和公式不显示(呈现为白框)的解决办法 目录 Word 2019打开.doc文档后图片和公式不显示(呈现为白框)的解决办法一、问题描述二、解决方法1.打开 WORD 2019,点击菜单中的“文件”;…...

三个整数排序
描述 给定三个整数,请将它们按从小到大的顺序输出。 输入 输入为一行,包含三个整数,用空格分隔。 输出 输出为一行,包含三个整数,用空格分隔,表示排序后的结果。 输入样例 1 9 3 7 输出样例 1 3 …...

Nginx反向代理出现错误 502 bad gateway 案例解析
场景描述 Nginx uwsgi flask Flask框架写的程序,使用uwsgi启动,Nginx作为反向代理调用Flask应用。 Flask应用有些操作时间比较长,会超过1分钟,在网页端访问会出现错误: 502 bad gateway。 Nginx的错误日志中会出现错误…...
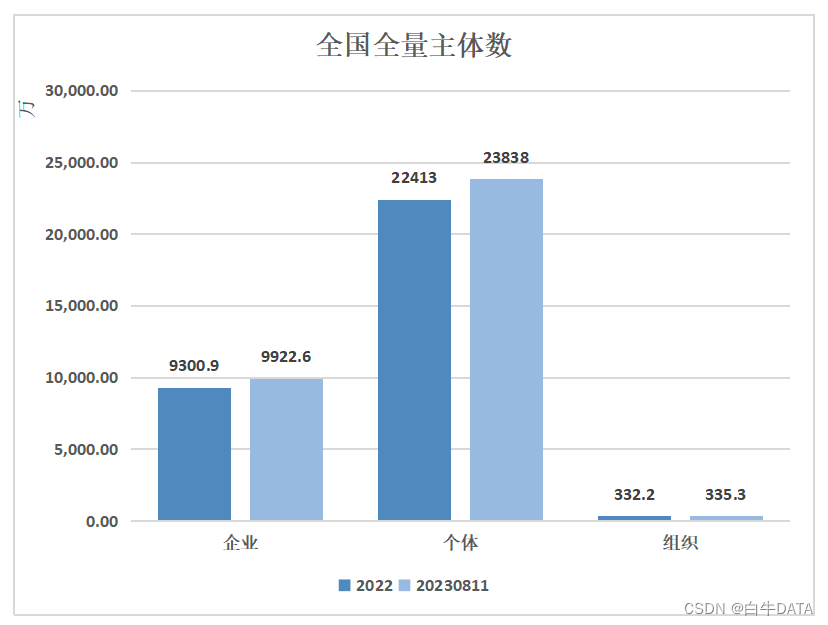
截止到目前全量主体总数有多少?
企业主体类型 企业主体类型有很多种,一般我们会分为公司(有限责任)、合伙企业、个人独资企业、个体经营户这些类别。 今天我们按照企业,个体,组织的分类方式来看各个主体的总数。 企业:统一社会信用代码…...

HTTP--Request详解
请求消息数据格式 请求行 请求方式 请求url 请求协议/版本 GET /login.html HTTP/1.1 请求头 客户端浏览器告诉服务器一些信息 请求头名称: 请求头值 常见的请求头: User-Agent:浏览器告诉服务器,我访问你使用的浏览器版本信息 可…...
 : TCP多线程一个server对应多个client)
Linux C++ 网络编程基础(2) : TCP多线程一个server对应多个client
目录 一、linux posix线程相关函数介绍二、tcp server基础版本三、tpc服务端多线程版本四、tpc客户端代码tcp编程时, 一个server可以对应多个client, server端用多线程可以实现. linux下多线程可以使用POSIX的线程函数, 下面给出服务端和客户端的代码. 一、linux posix线程相关…...

如何构建一个 NodeJS 影院微服务并使用 Docker 部署
文章目录 前言什么是微服务?构建电影目录微服务构建微服务从 NodeJS 连接到 MongoDB 数据库总结 前言 如何构建一个 NodeJS 影院微服务并使用 Docker 部署。在这个系列中,将构建一个 NodeJS 微服务,并使用 Docker Swarm 集群进行部署。 以下…...
--01)
BEVFusion(ICRA-2023)--01
说明:论文 BEVFusion: Multi-Task Multi-Sensor Fusion with Unified Bird’s-Eye View Representation 原代码运行记录 原始环境:python 3.9 torch 1.12 (失败) 报错: python setup.py develop/mmdet3d/ops/ball_qu…...

Java——Iterator迭代器
在程序开发中,经常需要遍历集合中的所有元素。针对这种需求,JDK专门提供了一个接口java.util.Iterator。Iterator接口也是Java集合中的一员,但它与Collection、Map接口有所不同,Collection接口与Map接口主要用于存储元素ÿ…...
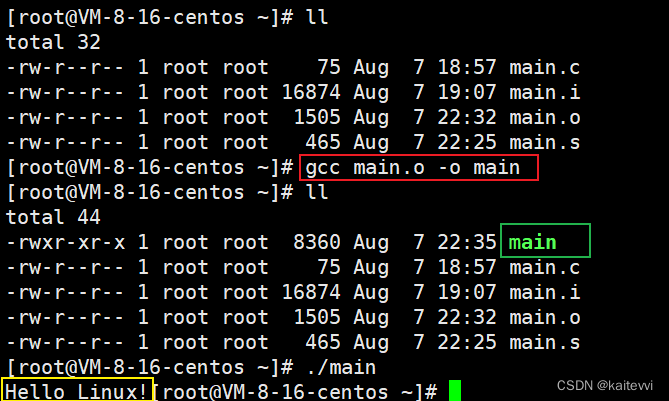
GCC编译过程:预处理->编译->汇编->链接
目录 引言 概括介绍 一、预处理 二、编译 三、汇编 四、链接 总结 引言 当使用集成开发环境(IDE)进行C语言编程时,点击"编译"按钮后,整个C程序从源代码到可执行文件的生成过程会自动完成。IDE会在后台为我们执行C…...

JVM笔记 —— 出现内存溢出错误时时如何排查
一、出现内存溢出的几种情况 内存溢出错误分为StackOverflowError和OutOfMemoryError,前者是栈中出现溢出,后者一般是堆或方法区出现溢出,简称OOM 1. 栈溢出 StackOverflowError 栈溢出一般都是因为没有正确的结束递归导致的,无…...

多级嵌套引入组件导致Vue提示子组件未注册问题
发生此问题的时候是页面解析的时报错的, 所以可以放在beforeCreate中执行注册组件这个时候是在页面运行时执行的,运行时编译就结束了 第一种:可以在父组件中动态注册组件 export default{beforeCreate(){//require是commonJS,commonJS导入ES…...

vue3+element-plus组件下拉列表,数组数据转成树形数据
引入组件 可以直接在项目中引入element-plus表格组件,如果需要变成下拉列表样式需要添加以下属性: row-key 必填 最好给数字或唯一属性 , 给每个节点设置id 不填的话 没有办法实现展开效果 load 这个是动态添加数据的 前提(开启…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...

嵌入式常见 CPU 架构
架构类型架构厂商芯片厂商典型芯片特点与应用场景PICRISC (8/16 位)MicrochipMicrochipPIC16F877A、PIC18F4550简化指令集,单周期执行;低功耗、CIP 独立外设;用于家电、小电机控制、安防面板等嵌入式场景8051CISC (8 位)Intel(原始…...
