LeetCode 1289. 下降路径最小和 II:通俗易懂地讲解O(n^2) + O(1)的做法
【LetMeFly】1289.下降路径最小和 II:通俗易懂地讲解O(n^2) + O(1)的做法
力扣题目链接:https://leetcode.cn/problems/minimum-falling-path-sum-ii/
给你一个 n x n 整数矩阵 arr ,请你返回 非零偏移下降路径 数字和的最小值。
非零偏移下降路径 定义为:从 arr 数组中的每一行选择一个数字,且按顺序选出来的数字中,相邻数字不在原数组的同一列。
示例 1:
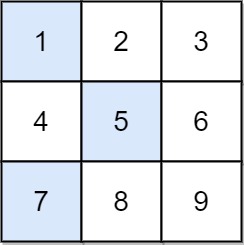
输入:arr = [[1,2,3],[4,5,6],[7,8,9]] 输出:13 解释: 所有非零偏移下降路径包括: [1,5,9], [1,5,7], [1,6,7], [1,6,8], [2,4,8], [2,4,9], [2,6,7], [2,6,8], [3,4,8], [3,4,9], [3,5,7], [3,5,9] 下降路径中数字和最小的是 [1,5,7] ,所以答案是 13 。
示例 2:
输入:grid = [[7]] 输出:7
提示:
n == grid.length == grid[i].length1 <= n <= 200-99 <= grid[i][j] <= 99
方法一:动态规划
这道题其实思路很简单:
- gird[i][j]来自gird[i - 1]的哪一个?当然是gird[i - 1]中最小的那一个。
- 如果grid[i - 1]中最小的那个元素恰好是j怎么办?那么gird[i][j]就来自gird[i - 1]中第二小的那一个。
不难发现,我们只关注上一行最小的两个元素(的位置)
具体实现
写一个函数findMin2(v),用来寻找数组v中最小的两个元素的位置。
用 i i i从第2行开始遍历地图grid:
- 用 j j j遍历 g i r d [ i ] gird[i] gird[i]:
- 如果 j j j等于上一行最小元素的下标: g r i d [ i ] [ j ] + = g r i d [ i − 1 ] [ 第二小元素的下标 ] grid[i][j] += grid[i - 1][第二小元素的下标] grid[i][j]+=grid[i−1][第二小元素的下标]
- 否则 g r i d [ i ] [ j ] + = g r i d [ i − 1 ] [ 最小元素的下标 ] grid[i][j] += grid[i - 1][最小元素的下标] grid[i][j]+=grid[i−1][最小元素的下标]
最终返回最后一行的最小元素即可。
- 时间复杂度 O ( n 2 ) O(n^2) O(n2),其中 s i z e ( g i r d ) = n × n size(gird) = n\times n size(gird)=n×n
- 空间复杂度 O ( 1 ) O(1) O(1)
AC代码
C++
class Solution {
private:pair<int, int> findMin2(vector<int>& v) { // 只接收长度大于等于2的vpair<int, int> ans;int m = v[0], loc = 0;for (int i = 0; i < v.size(); i++) {if (v[i] < m) {m = v[i], loc = i;}}ans.first = loc;loc = ans.first ? 0 : 1, m = v[loc]; // 如果第一个元素是最小的,那么找第二个最小元素的时候就从上一行的第二个元素开始for (int i = 0; i < v.size(); i++) {if (v[i] < m && i != ans.first) {m = v[i], loc = i;}}ans.second = loc;return ans;}
public:int minFallingPathSum(vector<vector<int>>& grid) {int n = grid.size();for (int i = 1; i < n; i++) {pair<int, int> last2min = findMin2(grid[i - 1]); // i >= 1说明grid[i - 1].size() >= 2for (int j = 0; j < n; j++) {grid[i][j] += (j == last2min.first ? grid[i - 1][last2min.second] : grid[i - 1][last2min.first]);}}return *min_element(grid.back().begin(), grid.back().end());}
};
Python
# from typing import Listclass Solution:def findMin2(self, v: List[int]) -> List[int]:ans = [0, 0]m, loc = v[0], 0for i in range(len(v)):if v[i] < m:m, loc = v[i], ians[0] = locloc = 0 if ans[0] else 1m = v[loc]for i in range(len(v)):if v[i] < m and i != ans[0]:m, loc = v[i], ians[1] = locreturn ansdef minFallingPathSum(self, grid: List[List[int]]) -> int:n = len(grid)for i in range(1, n):last2min = self.findMin2(grid[i - 1])for j in range(n):grid[i][j] += grid[i - 1][last2min[0]] if j != last2min[0] else grid[i - 1][last2min[1]]return min(grid[-1])
同步发文于CSDN,原创不易,转载请附上原文链接哦~
Tisfy:https://letmefly.blog.csdn.net/article/details/132201281
相关文章:

LeetCode 1289. 下降路径最小和 II:通俗易懂地讲解O(n^2) + O(1)的做法
【LetMeFly】1289.下降路径最小和 II:通俗易懂地讲解O(n^2) O(1)的做法 力扣题目链接:https://leetcode.cn/problems/minimum-falling-path-sum-ii/ 给你一个 n x n 整数矩阵 arr ,请你返回 非零偏移下降路径 数字和的最小值。 非零偏移下…...

Coin Change
一、题目 Suppose there are 5 types of coins: 50-cent, 25-cent, 10-cent, 5-cent, and 1-cent. We want to make changes with these coins for a given amount of money. For example, if we have 11 cents, then we can make changes with one 10-cent coin and one 1-c…...
2023 8 -14链表OJ
💕人面只今何处去,桃花依旧笑春风💕 作者:Mylvzi 文章主要内容:详解链表OJ题 题目一:环形链表(判断链表是否带环) 题目描述: 画图分析: 代码实现&#x…...
大数据必回之LSM树
LSM树(Log-Structured-Merge-Tree)并不像B、红黑树一样是一颗严格的树状数据结构,它其实是一种存储结构,像HBase、RocksDB这些NoSQL存储都是采用LSM树。它是一种分层、有序、面向磁盘的数据结构,核心思想是顺序写性能远…...

Vue中的Object.defineProperty详解
Vue中的Object.defineProperty是一个比较重要的方法,它是可以定义对象中属性的一个方法,相比于在对象中直接定义的对象,它更具有灵活性。 直接定义对象中的属性是这样的: let person {name:张三,address:广东,age:12,} 而Object.…...
MySQL高阶知识点(一)一条SQL【更新】语句是如何执行的
一条SQL【更新】语句是如何执行的 首先,可以确定的说,【查询】语句的那一套流程,【更新】语句也是同样会走一遍,与查询流程不一样的是, 更新语句涉及到【事务】,就必须保证事务的四大特性:ACID&…...

threejs实现模型gltf的动画效果
确保加载模型后模型有animations属性。加载完模型后,在模型中定义mixer的变量值。 // 4、加入加载器 const loader new GLTFLoader(); loader.load("./model/gltf/RobotExpressive/RobotExpressive.glb", function (gltf) {// 赋值动画给mixermixer ne…...

Harmony创建项目ohpm报错
Harmony创建FA模型的项目时报如下错: The registry is empty - edit .ohpmrc file or use "ohpm config set registry your_registry" command to set registry.解决方法: File -> Settings -> Build,Execution,Deployment -> Ohpm …...

44 | 酒店预订及取消的数据分析
1.背景介绍 数据集来自Kaggle网站上公开的Hotel booking demand项目 该数据集包含了一家城市酒店和一家度假酒店的预订信息,包括预订时间、入住时间、成人、儿童或婴儿数量、可用停车位数量等信息。 数据集容量约为12万32 本次数据分析主要包含如下内容: 总览数据,完成对…...

物联网和不断发展的ITSM
物联网将改变社会,整个技术行业关于对机器连接都通过嵌入式传感器、软件和收集和交换数据的电子设备每天都在更新中。Gartner 预测,全球将有4亿台互联设备投入使用。 无论企业采用物联网的速度如何,连接设备都将成为新常态,IT服务…...

加了ComponentScan,但是feign接口无法注入的原因
正文 正确的注入 如果发现无法注入:看看启动类Application是否有加入注解:EnableFeignClients(AppConstant.BASE_PACKAGES) 注意:EnableFeignClients和ComponentScan是两个独立的扫描,所以,如果只配置了ComponentSca…...

C#Winform中DataGridView控件显示行号实例
本文演示C#Winform中如何给DataGridView控件显示行号。 首先创建winform项目,添加DataGridView控件,给控件添加两列。 修改CS代码: using System.Windows.Forms;namespace DataGridviewDemo {public partial class Form1 : Form{public Form1(){InitializeComponent();//添…...
Stable Diffusion WebUI安装和使用教程(Windows)
目录 下载Stable Diffusion WebUI运行安装程序,双击webui.bat界面启动插件安装(github)模型下载(有些需要魔法)安装过程遇到的大坑总结参考的博客 整个过程坑巨多,我花了一个晚上的时间才全部搞定,本教程针对有编程基础…...

LeetCode 35题:搜索插入位置
题目 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 示例 1: 输入: nums [1,3,5,6], target 5 输出: 2示例 2:…...

Linux系统中常见的几种软件包管理器
软件包管理器 DPKGAPT(APT-GET)RPMYUMDNF Linux软件包管理工具是一组命令的集合,其作用是在操作系统中提供安装、更新、删除及卸载软件的方法,同时提供对系统中所有软件状态信息的查询。不同的Linux发行版会有不同的包管理器&…...

python异步IO完全指南
原地址:https://flyingbyte.cc/post/async_io/ python异步IO完全指南 做为一种并行编程的範式,异步IO在Python中非常受重视,从Python3.4到3.7快速演进。 我们已经有多线程,多进程,并发(concurrency&#x…...

打造企业或者个人IP引流法
打造企业或者个人IP引流法. 大家好,我是百收网SEO编辑:狂潮老师,今天给大家分享企业IP打造的方法 首先我们想让人知道你的企业叫什么,怎么找到你的企业 这个时候我们就需要去各大平台发布信息,客户想了解直接去搜索…...

TMC Self-Managed 提升跨多云环境安全性
作为云原生技术栈的关键技术之一,Kubernetes 被企业用户广泛试用并开始支撑实际业务应用运行,实现技术先进性带来的生产力提升。但与此同时,随着 Kubernetes 技术的不断广泛与深化使用,企业用户也开始面临诸多技术上的挑战&#x…...
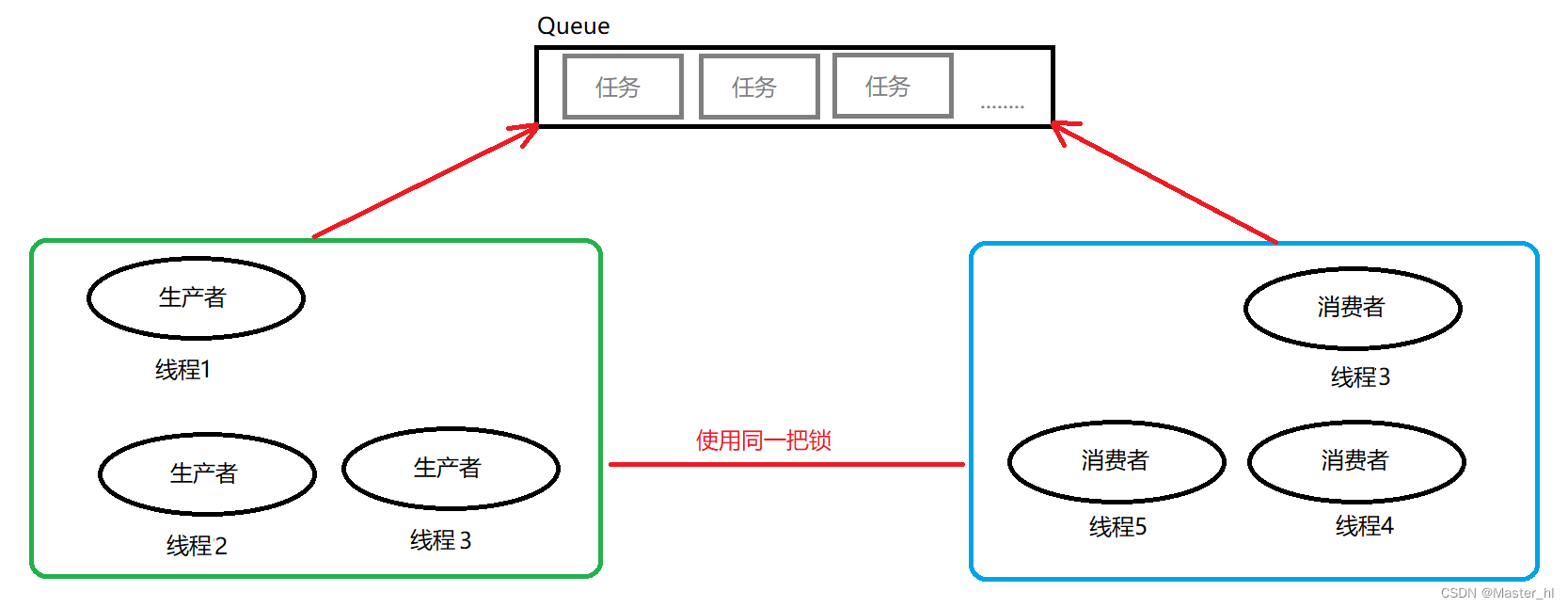
并发编程 - 线程间三种常见的通信手段
线程间通信是指多个线程之间通过某种机制进行协调和交互,例如:线程等待和通知机制就是线程通讯的主要手段之一。 在 Java 中有以下三种实现线程等待的手段 : Object 类提供的 wait(),notify() 和 notifyAll() 方法;C…...

iperf3命令使用说明
iperf3 是一款网络性能测试工具,用于在TCP和UDP数据流之间测量最大带宽。它可以帮助您测试网络连接的速度、延迟、丢包等参数。以下是一些常用的选项和参数的解释: 通用选项: -s 或 --server:运行服务器模式。-c 或 --client &l…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...
