线段树-模板-区间查询-区间修改
【模板】线段树 2
传送门:https://www.luogu.com.cn/problem/P3373
题单:https://www.luogu.com.cn/training/16376#problems
题目描述
如题,已知一个数列,你需要进行下面三种操作:
- 将某区间每一个数乘上 x x x;
- 将某区间每一个数加上 x x x;
- 求出某区间每一个数的和。
输入格式
第一行包含三个整数 n , q , m n,q,m n,q,m,分别表示该数列数字的个数、操作的总个数和模数。
第二行包含 n n n 个用空格分隔的整数,其中第 i i i 个数字表示数列第 i i i 项的初始值。
接下来 q q q 行每行包含若干个整数,表示一个操作,具体如下:
操作 1 1 1: 格式:1 x y k 含义:将区间 [ x , y ] [x,y] [x,y] 内每个数乘上 k k k
操作 2 2 2: 格式:2 x y k 含义:将区间 [ x , y ] [x,y] [x,y] 内每个数加上 k k k
操作 3 3 3: 格式:3 x y 含义:输出区间 [ x , y ] [x,y] [x,y] 内每个数的和对 m m m 取模所得的结果
输出格式
输出包含若干行整数,即为所有操作 3 3 3 的结果。
样例 #1
样例输入 #1
5 5 38
1 5 4 2 3
2 1 4 1
3 2 5
1 2 4 2
2 3 5 5
3 1 4
样例输出 #1
17
2
提示
【数据范围】
对于 30 % 30\% 30% 的数据: n ≤ 8 n \le 8 n≤8, q ≤ 10 q \le 10 q≤10。
对于 70 % 70\% 70% 的数据:$n \le 10^3 , , ,q \le 10^4$。
对于 100 % 100\% 100% 的数据: 1 ≤ n ≤ 1 0 5 1 \le n \le 10^5 1≤n≤105, 1 ≤ q ≤ 1 0 5 1 \le q \le 10^5 1≤q≤105。
除样例外, m = 571373 m = 571373 m=571373。
(数据已经过加强 _)
样例说明:
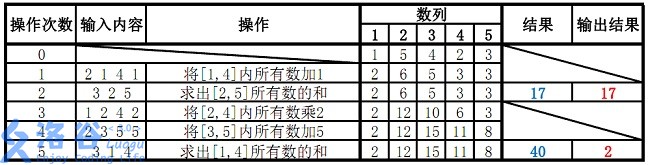
故输出应为 17 17 17、 2 2 2( 40 m o d 38 = 2 40 \bmod 38 = 2 40mod38=2)。
代码
#include <bits/stdc++.h>#define MAXN 100010
#define ll long longusing namespace std;int n, m, mod;
int a[MAXN];struct Segment_Tree {ll sum, add, mul;int l, r;
}s[MAXN * 4];void update(int pos) {s[pos].sum = (s[pos << 1].sum + s[pos << 1 | 1].sum) % mod;return;
}void pushdown(int pos) { //pushdown的维护s[pos << 1].sum = (s[pos << 1].sum * s[pos].mul + s[pos].add * (s[pos << 1].r - s[pos << 1].l + 1)) % mod;s[pos << 1 | 1].sum = (s[pos << 1 | 1].sum * s[pos].mul + s[pos].add * (s[pos << 1 | 1].r - s[pos << 1 | 1].l + 1)) % mod;s[pos << 1].mul = (s[pos << 1].mul * s[pos].mul) % mod;s[pos << 1 | 1].mul = (s[pos << 1 | 1].mul * s[pos].mul) % mod;s[pos << 1].add = (s[pos << 1].add * s[pos].mul + s[pos].add) % mod;s[pos << 1 | 1].add = (s[pos << 1 | 1].add * s[pos].mul + s[pos].add) % mod;s[pos].add = 0;s[pos].mul = 1;return;
}void build_tree(int pos, int l, int r) { //建树s[pos].l = l;s[pos].r = r;s[pos].mul = 1;if (l == r) {s[pos].sum = a[l] % mod;return;}int mid = (l + r) >> 1;build_tree(pos << 1, l, mid);build_tree(pos << 1 | 1, mid + 1, r);update(pos);return;
}void ChangeMul(int pos, int x, int y, int k) { //区间乘法if (x <= s[pos].l && s[pos].r <= y) {s[pos].add = (s[pos].add * k) % mod;s[pos].mul = (s[pos].mul * k) % mod;s[pos].sum = (s[pos].sum * k) % mod;return;}pushdown(pos);int mid = (s[pos].l + s[pos].r) >> 1;if (x <= mid) ChangeMul(pos << 1, x, y, k);if (y > mid) ChangeMul(pos << 1 | 1, x, y, k);update(pos);return;
}void ChangeAdd(int pos, int x, int y, int k) { //区间加法if (x <= s[pos].l && s[pos].r <= y) {s[pos].add = (s[pos].add + k) % mod;s[pos].sum = (s[pos].sum + k * (s[pos].r - s[pos].l + 1)) % mod;return;}pushdown(pos);int mid = (s[pos].l + s[pos].r) >> 1;if (x <= mid) ChangeAdd(pos << 1, x, y, k);if (y > mid) ChangeAdd(pos << 1 | 1, x, y, k);update(pos);return;
}ll AskRange(int pos, int x, int y) { //区间询问if (x <= s[pos].l && s[pos].r <= y) {return s[pos].sum;}pushdown(pos);ll val = 0;int mid = (s[pos].l + s[pos].r) >> 1;if (x <= mid) val = (val + AskRange(pos << 1, x, y)) % mod;if (y > mid) val = (val + AskRange(pos << 1 | 1, x, y)) % mod;return val;
}int main() {scanf("%d%d%d", &n, &m, &mod);for (int i = 1; i <= n; i++) {scanf("%d", &a[i]);}build_tree(1, 1, n);for (int i = 1; i <= m; i++) {int opt, x, y;scanf("%d%d%d", &opt, &x, &y);if (opt == 1) {int k;scanf("%d", &k);ChangeMul(1, x, y, k);}if (opt == 2) {int k;scanf("%d", &k);ChangeAdd(1, x, y, k);}if (opt == 3) {printf("%lld\n", AskRange(1, x, y));}}return 0;
}
相关文章:

线段树-模板-区间查询-区间修改
【模板】线段树 2 传送门:https://www.luogu.com.cn/problem/P3373 题单:https://www.luogu.com.cn/training/16376#problems 题目描述 如题,已知一个数列,你需要进行下面三种操作: 将某区间每一个数乘上 x x x&a…...

微服务架构和分布式架构的区别
微服务架构和分布式架构的区别 有:1、含义不同;2、概念层面不同;3、解决问题不同;4、部署方式不同;5、耦合度不同。其中,含义不同指微服务架构是一种将一个单一应用程序开发为一组小型服务的方法ÿ…...
Ajax-概念、Http协议、Ajax请求及其常见问题
Ajax Ajax概念Ajax优缺点HTTP协议请求报文响应报文 Ajax案例准备工作express基本使用创建一个服务器 发送AJAX请求GET请求POST请求JSON响应 Ajax请求出现的问题IE缓存问题Ajax请求超时与网络异常处理Ajax手动取消请求Ajax重复发送请求问题 Ajax概念 AJAX 全称为Asynchronous J…...
react 09之状态管理工具1 redux+ react-thunk的使用实现跨组件状态管理与异步操作
目录 react 09之状态管理工具1 redux react-thunk的使用实现跨组件状态管理与异步操作store / index.js store的入口文件index.js 在项目入口文件 引入store / actionType.js 定义action的唯一标识store / reducers / index.jsstore / actions / form.jsstore / reducers / for…...
opencv实战项目 手势识别-实现尺寸缩放效果
手势识别系列文章目录 手势识别是一种人机交互技术,通过识别人的手势动作,从而实现对计算机、智能手机、智能电视等设备的操作和控制。 1. opencv实现手部追踪(定位手部关键点) 2.opencv实战项目 实现手势跟踪并返回位置信息&…...

Netty对HPACK头部压缩的支持
前言 HTTP2终于支持对头部进行压缩传输了,Netty很早就支持HTTP2了,看下Netty对HPACK的实现源码,可以对HPACK理解的更深一下。 HpackDecoder Netty内置的编解码器Http2FrameCodec专门用来对HTTP2的各种Frame进行编解码,其中就包…...

C++:替换string中的字符
1.按照位置进行替换 string的成员函数replace可以满足这种需求,其变体有很多种,请参考官方文档,以下列举常用的两种: #include <iostream> #include <string> using namespace std;int main() {string s = "hello world";s.replace(s.begin(), s.b…...

【ChatGPT】自我救赎
ChatGPT辅助学习C之【在C中如果大数据类型转小数据类型会发生什么呢?】,今天问ChatGPT一个问题,让它解析下面这个C程序: #include <iostream> #include <cstdio> using namespace std; int main() {int a;long long b532165478…...
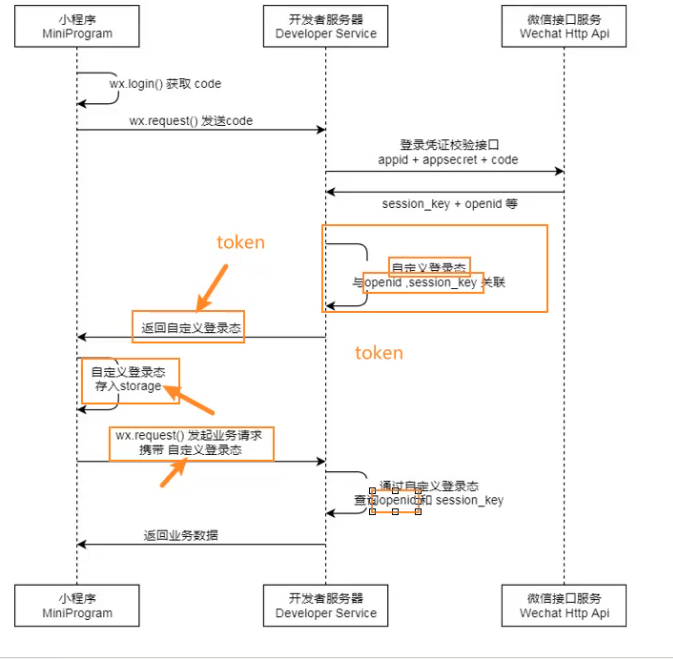
微信小程序(由浅到深)
文章目录 一. 项目基本配置1. 项目组成2. 常见的配置文件解析3. app.json全局的五大配置4.单个页面中的page配置5. App函数6.tabBar配置 二. 基本语法,事件,单位1. 语法2. 事件3. 单位 三. 数据响应式修改四 . 内置组件1. button2. image3. input4. 组件…...
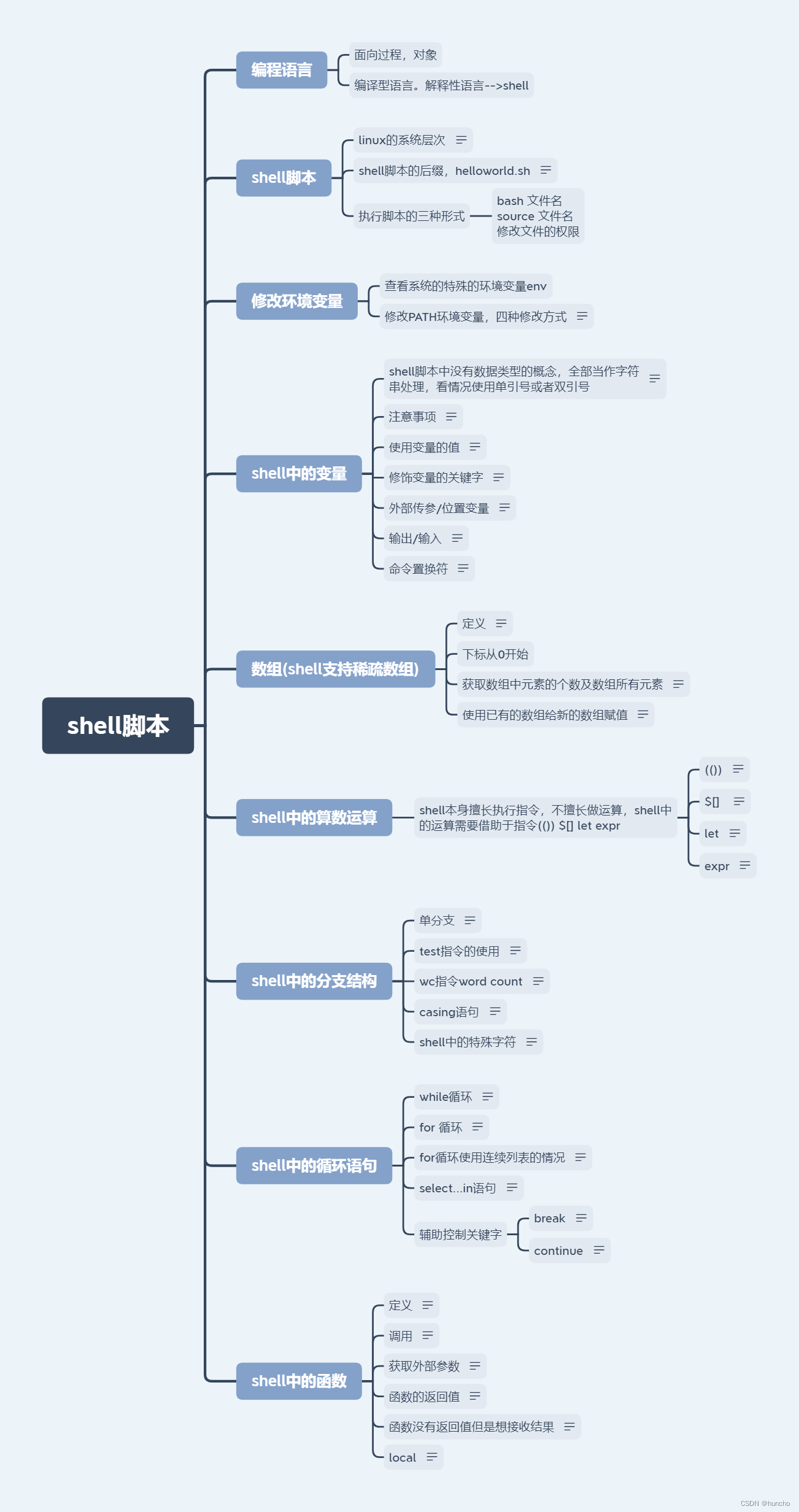
冒泡排序 简单选择排序 插入排序 快速排序
bubblesort 两个for循环,从最右端开始一个一个逐渐有序 #include <stdio.h> #include <string.h> #include <stdlib.h>void bubble(int *arr, int len); int main(int argc, char *argv[]) {int arr[] {1, 2, 3, 4, 5, 6, 7};int len sizeof(…...
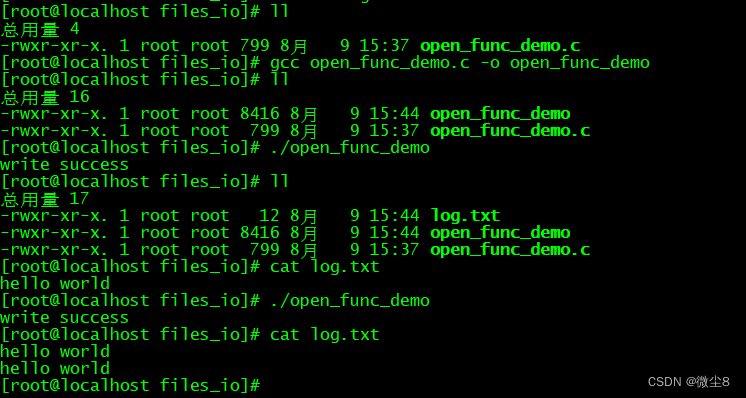
linux文件I/O之 open() 函数用法
#include <sys/types.h> #include <sys/stat.h> #include <fcntl.h> typedef unsigned int mode_t ; int open(const char *pathname, int flags); int open(const char *pathname, int flags, mode_t mode); 函数功能 打开或创建一个文件 返回值 成功…...

用Java操作MySQL数据库
新建Maven项目 创建Maven项目 添加依赖 在pom.xml的标签里加上下面的内容 如果是MySQL 5.8那么的版本号是5.x.x, 例如5.1.49 如果是MySQL 8.0那么的版本号是8.x.x, 例如 8.0.28 <dependencies><!-- https://mvnrepository.com/artifact/mysql/mysql-connector-java …...
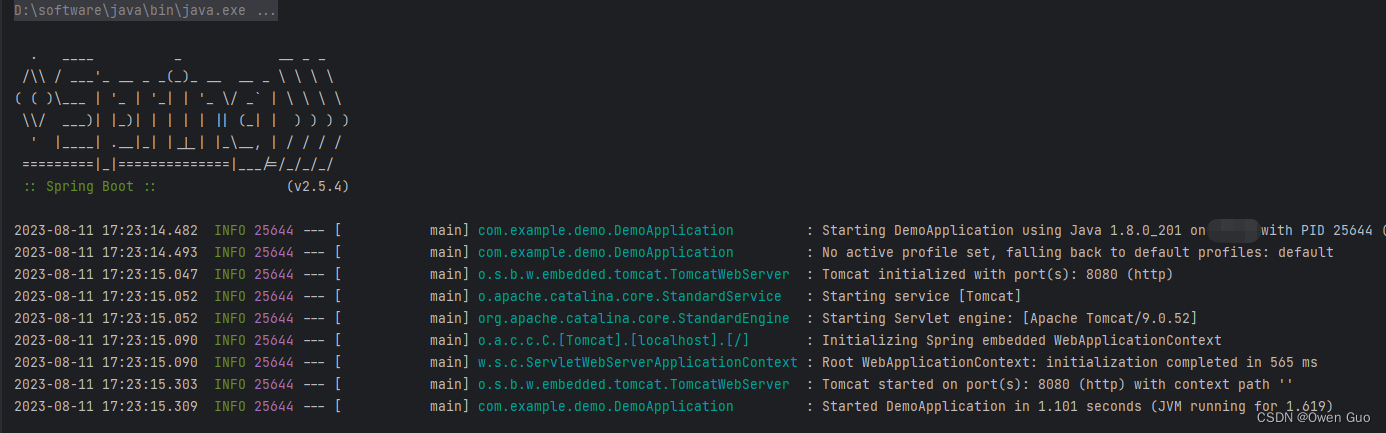
SpringBoot启动报错:java: 无法访问org.springframework.boot.SpringApplication
报错原因:jdk 1.8版本与SpringBoot 3.1.2版本不匹配 解决方案:将SpringBoot版本降到2系列版本(例如2.5.4)。如下图: 修改版本后切记刷新Meavn依赖 然后重新启动即可成功。如下图:...

Vue3 setup语法糖 解决富文本编辑器上传图片64位码过长问题 quill-image-extend-module
引言: 富文本编辑器传图片会解码成64位,非常长导致数据库会报错第一种方法:将数据库类型改成 mediumtext第二种办法:本文中的方法 说明,本周文所用语法糖为Vue3 setup语法,即<script setup> 思路 拦…...
、国测局坐标(火星坐标,GCJ02)、和WGS84坐标系之间的转换)
百度坐标(BD09)、国测局坐标(火星坐标,GCJ02)、和WGS84坐标系之间的转换
<!DOCTYPE html> <html><head><meta charset="UTF-8"><title></title></head><body><script>/*** * 百度坐标(BD09)、国测局坐标(火星坐标,GCJ02)、和WGS84坐标系之间的转换*///定义一些常量var x_PI = …...

论文浅尝 | CI4MRC:基于因果推断去除机器阅读理解中的名字偏差
笔记整理:朱珈徵,天津大学硕士,研究方向:问答 链接:https://aclanthology.org/2023.findings-acl.812/ 动机 机器阅读理解(Machine Reading Comprehension,MRC)是根据给定的文章回答…...

【校招VIP】测试计划之黑盒测试白盒测试
考点介绍: 黑盒测试&白盒测试是大厂和三四线公司校招的必考点。黑盒是以结果说话,白盒往往需要理解实现逻辑。现在商业项目的接口测试往往以白盒为主,也就是需要测试同学自己观察和修改数据库的值进行用例的测试。 但是无论采用哪种测试方…...

学习笔记整理-JS-01-语法与变量
文章目录 一、语法与变量1. 初识JavaScript2. JavaScript的历史3. JavaScript与ECMAScript的关系4. JavaScript的体系5. JavaScript的语言风格和特性 二、语法1. JavaScript的书写位置2. 认识输出语句3. REPL环境,交互式解析器4. 变量是什么5. 重点内容 一、语法与变…...

PHP之PHPExcel
include PHPExcel.php; include PHPExcel/Writer/Excel2007.php; //或者include PHPExcel/Writer/Excel5.php; 用于输出.xls的 //创建一个excel $objPHPExcel new PHPExcel(); // 输出Excel表格到浏览器下载 header(Content-Type: application/vnd.ms-excel); header(Content-…...
Redis系列(一):深入了解Redis数据类型和底层数据结构
Redis有以下几种常用的数据类型: redis数据是如何组织的 为了实现从键到值的快速访问,Redis 使用了一个哈希表来保存所有键值对。 Redis全局哈希表(Global Hash Table)是指在Redis数据库内部用于存储所有键值对的主要数据结构。…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...

spring Security对RBAC及其ABAC的支持使用
RBAC (基于角色的访问控制) RBAC (Role-Based Access Control) 是 Spring Security 中最常用的权限模型,它将权限分配给角色,再将角色分配给用户。 RBAC 核心实现 1. 数据库设计 users roles permissions ------- ------…...
