Tree相关
1.树相关题目
1.1 二叉树的中序遍历(简单):递归
题目:使用中序遍历二叉树
思想:按照访问左子树——根节点——右子树的方式遍历这棵树,而在访问左子树或者右子树的时候我们按照同样的方式遍历,直到遍历完整棵树
总结:对于一棵树而言,从根节点出发,有左子树和右子树;而对于左子树和右子树而言,根节点下的第一个左子树节点可以看作一个新的根节点,依次类推,因此在树种大部分会使用到递归这个概念
代码:定义 inorder(root) 表示当前遍历到 root 节点的答案
public class TreeNode{int val;TreeNode left;TreeNode right;TreeNode(){}TreeNode(int val){this.val = val;}TreeNode(int val,TreeNode tight,TreeNode left){this.val = val;this.left = left;this.right = right; }
}
class Solution{public List<Integer> inorderTraversal(TreeNode root){List<Integer> list = new ArrayList<>();inorder(root,list);return list;}public void inorder(TreeNode root,List<Integer> list){if(root == null){return;}//遍历左子树inorder(root.left,list);//加入中间节点list.add(root.val);//遍历右子树inorder(root.right,list);}
}1.2 不同的二叉搜索树Ⅰ(中等):动态规划
题目:给一个节点,求出有多少种不同的二叉搜索树
思想:因此在生成所有可行的二叉搜索树的时候,假设当前序列长度为 n,如果我们枚举根节点的值为 i,那么根据二叉搜索树的性质我们可以知道左子树的节点值的集合为 1…i−1[1…i−1],右子树的节点值的集合为 i+1…n[i+1…n]。使用动态规划来求解本题;则根为 i 的所有二叉搜索树的集合是左子树集合和右子树集合的笛卡尔积,对于笛卡尔积中的每个元素,加上根节点之后形成完整的二叉搜索树
笛卡尔积:笛卡尔积是一种数学运算,它将两个集合的元素分别组合起来,生成一个新的集合。新集合中的每个元素都是由两个集合中的一个元素组成的有序对,其中第一个元素来自第一个集合,第二个元素来自第二个集合。简单来说,就是将两个集合中的元素进行组合,生成所有可能的组合情况。
例如,有两个集合A={1,2}和B={a,b},它们的笛卡尔积为{(1,a),(1,b),(2,a),(2,b)}。其中,第一个元素为1或2,第二个元素为a或b,共有4种组合情况。
总结:对于一组任意序列而言,能够产生的二叉搜索树是很多的;根据二叉搜索树的定义约束,我们可以任意选用根节点,然后选择根节点的左边和右边序列组成所有可能的左子树和右子树,最终连接即可;公式为:
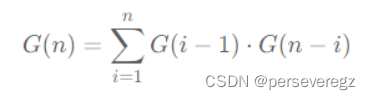
代码:
class Solution {public int numTrees(int n) {//G为n+1是为了存G[0]int[] G = new int[n+1];G[0] = 1;G[1] = 1;
//由于G[n] = Σ(G[i -1]*G[n-i]);//将i当作n,对应求和中的上限nfor(int i =2 ; i <= n; ++i){//将j当作i。对应求和中的遍历ifor(int j = 1; j <= i ; ++j){G[i] += G[j - 1] * G[i - j]; }}return G[n];}
}1.3 不同的二叉搜索树Ⅱ(中等):回溯
题目:给一个节点,将这个节点有多少种二叉搜索树全部展示出来
思想:二叉搜索树BST的性质为:根节点的值大于左子树所有节点的值,小于右子树所有节点的值,且左子树和右子树也同样为二叉搜索树;因此在生成所有可行的二叉搜索树的时候,假设当前序列长度为 n,如果我们枚举根节点的值为 i,那么根据二叉搜索树的性质我们可以知道左子树的节点值的集合为 1…i−1[1…i−1],右子树的节点值的集合为 i+1…n[i+1…n]。而左子树和右子树的生成相较于原问题是一个序列长度缩小的子问题;采用回溯的方法来解决这道题目
总结:与第一题类似,我们展示所有的二叉搜索树也可以选用不同的根节点,将根节点两边序列分别递归得到左右子树,组合为一个树即可
代码:
public class TreeNode{int val;TreeNode left;TreeNode right;TreeNode(){}TreeNode(int val){this.val = val;}TreeNode(int val,TreeNode tight,TreeNode left){this.val = val;this.left = left;this.right = right; }
}
class Solution {public List<TreeNode> generateTrees(int n) {if (n == 0) {return new LinkedList<TreeNode>();}return generateTrees(1, n);}
public List<TreeNode> generateTrees(int start, int end) {List<TreeNode> allTrees = new LinkedList<TreeNode>();if (start > end) {allTrees.add(null);return allTrees;}
// 枚举可行根节点;每一个都可以做根节点for (int i = start; i <= end; i++) {//用相同的方法做两次相同的行为// 获得所有可行的左子树集合List<TreeNode> leftTrees = generateTrees(start, i - 1);
// 获得所有可行的右子树集合List<TreeNode> rightTrees = generateTrees(i + 1, end);
//将可行的左子树、右子树、根节点组合// 从左子树集合中选出一棵左子树,从右子树集合中选出一棵右子树,拼接到根节点上for (TreeNode left : leftTrees) {for (TreeNode right : rightTrees) {TreeNode currTree = new TreeNode(i);currTree.left = left;currTree.right = right;allTrees.add(currTree);}}}return allTrees;}
}1.4 验证二叉搜索树(中等)
题目:给一个二叉树的根节点,判断是否是有效的二叉搜索树
思想:如果该二叉树的左子树不为空,则左子树上所有节点的值均小于它的根节点的值; 若它的右子树不空,则右子树上所有节点的值均大于它的根节点的值;它的左右子树也为二叉搜索树
总结:二叉搜索树的性质是左边子树值均小于根节点,右边子树值均大于根节点,且其左右子树也满足该性质,左右子树的判断进行递归即可;此题的思想一样是:利用根节点的左右两端小于/大于的情况,生成判断isValidBST(root,Long.MIN_VALUE,Long.MAX_VALUE)
代码:什么是递归?就是大的用的方法,小的也用到了,那就一起用
class Solution {public boolean isValidBST(TreeNode root) {return isValidBST(root,Long.MIN_VALUE,Long.MAX_VALUE);}
public boolean isValidBST(TreeNode root,long lower,long upper){if(root == null){return true;}if(root.val <= lower || root.val >= upper){return false;}
//对于root的左节点而言,都小于根节点;对于root的右节点而言,都大于根节点return isValidBST(root.left,lower,root.val) && isValidBST(root.right,root.val,upper);}
}1.5 二叉树的层序遍历(中等):广度优先搜索+队列
题目:给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)
思想:创建一个队列,从根节点开始入队出队,然后是左右子节点入队出队;如果队列不为空:若队列长度为s,则遍历s输出即可
总结:使用队列的方式:先将根节点入队,然后让左右子节点以此入队出队即可;先判断队列是否为空,然后根据队列长度输出元素
代码:
class Solution {public List<List<Integer>> levelOrder(TreeNode root) {List<List<Integer>> res = new ArrayList<>();if(root == null){return res;}//创建一个队列Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);//判断是否为空while(!queue.isEmpty()){List<Integer> list = new ArrayList<>();int len = queue.size();//根据长度出队for(int i = 1; i <= len; ++i){TreeNode currRoot = queue.poll();if(currRoot.left != null){queue.offer(currRoot.left);}if(currRoot.right != null){queue.offer(currRoot.right);}list.add(currRoot.val);}res.add(list);}return res;}
}1.6 相同的树(简单):深度优先搜索+递归
题目:给你两棵二叉树的根节点 p 和 q ,编写一个函数来检验这两棵树是否相同
思想:
-
判断是否为空
-
如果两个二叉树都为空,则两个二叉树相同
-
如果两个二叉树中有且只有一个为空,则两个二叉树一定不相同。
-
-
如果两个二叉树都不为空,判断根节点与左右子树
-
那么首先判断它们的根节点的值是否相同,若不相同则两个二叉树一定不同,
-
若相同,再分别判断两个二叉树的左子树是否相同以及右子树是否相同
-
这是一个递归的过程,因此可以使用深度优先搜索,递归地判断两个二叉树是否相同
-
总结:判断树是否相同:利用深度优先搜索;判断是否都为空、根节点是否相同、子树是否相同
代码:什么是递归?就是大的用的方法,小的也用到了,那就一起用
什么是深度优先搜索?从上往下依次搜索
lass Solution {public boolean isSameTree(TreeNode p, TreeNode q) {//是否为空if(p == null && q == null){return true;}//是否只有一个为空else if(p == null || q == null){return false;}//根节点是否相同else if(p.val != q.val){return false;}//左右子树是否相同else{return isSameTree(p.left,q.left) && isSameTree(p.right,q.right);}}
}1.7 从前序与中序遍历序列构造二叉树(中等):递归
题目:给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的前序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。
思想:只要我们在中序遍历中定位到根节点,那么我们就可以分别知道左子树和右子树中的节点数目。由于同一颗子树的前序遍历和中序遍历的长度显然是相同的,因此我们就可以对应到前序遍历的结果中,对上述形式中的所有左右括号进行定位
总结:前序遍历和中序遍历都给出了所有树节点;前序第一个节点就是根节点,将其找到,在中序遍历中就能得到根节点的左右子树节点的个数,然后根据其个数将其递归组合为一个二叉树即可
代码:
class Solution {private Map<Integer, Integer> indexMap;
public TreeNode buildTree(int[] preorder, int[] inorder) {int n = preorder.length;// 构造哈希映射,帮助我们快速定位根节点indexMap = new HashMap<Integer, Integer>();for (int i = 0; i < n; i++) {indexMap.put(inorder[i], i);}return myBuildTree(preorder, inorder, 0, n - 1, 0, n - 1);}public TreeNode myBuildTree(int[] preorder, int[] inorder, int preorder_left, int preorder_right, int inorder_left, int inorder_right) {if (preorder_left > preorder_right) {return null;}
// 前序遍历中的第一个节点就是根节点int preorder_root = preorder_left;// 在中序遍历中定位根节点int inorder_root = indexMap.get(preorder[preorder_root]);// 先把根节点建立出来TreeNode root = new TreeNode(preorder[preorder_root]);// 得到左子树中的节点数目int size_left_subtree = inorder_root - inorder_left;// 递归地构造左子树,并连接到根节点//先序遍历中「从 左边界+1 开始的 size_left_subtree」个元素就对应了中序遍历中「从 左边界 开始到 根节点定位-1」的元素root.left = myBuildTree(preorder, inorder, preorder_left + 1, preorder_left + size_left_subtree, inorder_left, inorder_root - 1);// 递归地构造右子树,并连接到根节点// 先序遍历中「从 左边界+1+左子树节点数目 开始到 右边界」的元素就对应了中序遍历中「从 根节点定位+1 到 右边界」的元素root.right = myBuildTree(preorder, inorder, preorder_left + size_left_subtree + 1, preorder_right, inorder_root + 1, inorder_right);return root;}
}1.8 平衡二叉树(简单):自顶向下+递归
题目:给定一个二叉树,判断它是否是高度平衡的二叉树;
-
高度平衡:一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1
-
二叉树的高度:其左右子树的最大高度+1
思想:一棵二叉树是平衡二叉树,当且仅当其所有子树也都是平衡二叉树,因此可以使用递归的方式判断二叉树是不是平衡二叉树,递归的顺序可以是自顶向下或者自底向上

总结:在做树的题时,都要先将root == null的情况一判断;然后根据题目去求解;比如平衡二叉树按照定义来做:左右子树高度差小于等于1,左右子树也都为平衡二叉树;节点高度是左右子树最大高度 + 1
代码:
class Solution {public boolean isBalanced(TreeNode root) {if(root == null){return true;}//平衡二叉树://左右子树高度差 <= 1 且 左右子树也均为平衡二叉树return Math.abs(height(root.left) - height(root.right)) <= 1 && isBalanced(root.left) && isBalanced(root.right);}
public int height(TreeNode root){if(root == null){return 0;}//二叉树的高度为:左右子树最大高度 + 1return Math.max(height(root.left),height(root.right)) + 1;}
}1.9 二叉树的最小深度(简单):深度优先搜索/广度优先搜索 + 递归
题目:给定一个二叉树,找出其最小深度;最小深度是从根节点到最近叶子节点的最短路径上的节点数量
思想:深度优先搜索:
-
如果根节点为空,返回0
-
如果只有根节点,返回1
-
如果有左右子树,则最小深度就是左右子树的最小深度 + 1
-
-
总结:深度优先搜索可以将问题拆分为小问题,然后利用递归来解决
代码:
class Solution {public int minDepth(TreeNode root) {//如果没有根节点,返回0if(root == null){return 0;}
//如果只有根节点,返回1if(root.left == null && root.right == null){return 1;}
int min_Depth = Integer.MAX_VALUE;//如果有子树:分别比较左右子树深度哪个更小,然后将其加1并返回if(root.left != null){min_Depth = Math.min(minDepth(root.left),min_Depth);}if(root.right != null){min_Depth = Math.min(minDepth(root.right),min_Depth);}
return min_Depth + 1;}
}1.10 二叉树展开为链表(中等):前序遍历
题目:给你二叉树的根结点 root ,请你将它展开为一个单链表;
-
展开后的单链表应该同样使用
TreeNode,其中right子指针指向链表中下一个结点,而左子指针始终为null。 -
展开后的单链表应该与二叉树先序遍历顺序相同。
思想:先前序遍历得到单链表的顺序,然后将各节点的左节点指向null,右节点指向下一个前序遍历中的节点
总结:深度优先搜索可以将问题拆分为小问题,然后利用递归来解决
代码:
class Solution {public void flatten(TreeNode root) {//先拿到前序遍历后的节点(注意此时不是要值,因此可以不用取树的值),作为单链表展开后的顺序List<TreeNode> list = new ArrayList<>();preorder(root,list);
//将单链表左节点设为null,右节点赋为先序遍历的下一个值//这里长度为 list.size() - 1,因为倒数第二个节点可以有左右子节点,但倒数第一个节点肯定是没有左右子节点的for(int i = 0; i < list.size() - 1; i++){TreeNode prev = list.get(i);prev.left = null;prev.right = list.get(i + 1);}}
public void preorder(TreeNode root,List<TreeNode> list){if(root == null){return;}list.add(root);preorder(root.left,list);preorder(root.right,list);}
}1.11 二叉树的最近公共祖先(中等):递归
题目:给定一个二叉树, 找到该树中两个指定节点的最近公共祖先
-
最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
思想:两种情况:
-
公共祖先不是自己
-
公共祖先是自己
因此可以先定义一个函数:fx:表示x节点的子树中是否包含p或者q

总结:首先需要读懂题意,然后才能入手解决这种较为复杂的问题,可以设置一个专门判断是否存在节点p、q的函数,从而根据两种情况递归的使用该函数,最终得到结果
代码:
class Solution {
//用来保存最近公共祖先private TreeNode res;
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {isSon(root,p,q);return this.res;}
//定义一个函数,用来检查root中是否包含p或者q,是则返回true(该方法无法直接找到公共祖先,而是找到包含p或者q的节点)public boolean isSon(TreeNode root,TreeNode p,TreeNode q){if(root == null){return false;}//root的左子节点包含p或qboolean lson = isSon(root.left,p,q);//root的右子节点包含p或者qboolean rson = isSon(root.right,p,q);//如果root的左右子节点各包含了p、q,说明root就是最近公共祖先节点if(lson && rson){this.res = root;}//如果root本身就是q或者q,则root就是最近公共祖先if((root.val == p.val || root.val == q.val) && (lson || rson)){this.res = root;}//若左子树、右子树、节点本身就包含p或者q,就返回truereturn lson || rson || (root.val == p.val || root.val == q.val);}
}1.12 填充每个节点的下一个右侧节点指针(中等):层次遍历
题目:给定一个 完美二叉树 ,其所有叶子节点都在同一层,每个父节点都有两个子节点,填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。
思想:对二叉树进行层次遍历,然后对其节点进行右侧指针连接
总结:只需进行层次遍历,便能够得到每个节点,然后队列出队时,只要不是倒数第一个元素就将队列头部元素赋给出队元素指针即可
代码:
补充:Java中Queue共有6个方法:
1、offer函数和add函数的区别
在一个满的队列中加入一个新项,多出的项就会被拒绝。
add() :在队列中添加元素;若队列已满抛出 unchecked 异常
offer() :在队列中添加元素;若队列已满返回 false。
2、poll函数和remove函数的区别
remove():从队列中删除第一个元素;若集合为空返回异常
poll() :从队列中删除第一个元素;若集合为空返回null
3、peek函数和element函数的区别
element() :在队列头部查询元素;若集合为空返回异常
peek() :在队列头部查询元素;若集合为空返回null
class Solution {public Node connect(Node root) {if(root == null){return root;}
//创建队列用来进行层次遍历时的入队出队Queue<Node> queue = new LinkedList<>();queue.add(root);
//循环:先判断queue是否为空,不为空则遍历queue所有元素出队操作while(!queue.isEmpty()){int len = queue.size();for(int i = 0; i < len; i++){
Node node = queue.poll();
//在层序遍历中加入:连接右侧指针操作if(i < len - 1){//查询此时queue中的头部元素,将其赋给node指针nextnode.next = queue.peek();}
if(node.left != null){queue.add(node.left);}if(node.right != null){queue.add(node.right);}}}return root;}
}1.13 二叉树的右视图(中等):深度优先搜索/广度优先搜索
题目:给定一个二叉树的 根节点 root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值
思想:对树进行深度优先搜索,搜索过程中,先访问右子树,则第一个节点就是最右边的节点;知道树的层数,就能得到最终的结果数组
总结:要注意当右侧没有节点时,左子树节点的值也是右侧视图能够看到的节点
代码:
class Solution {public List<Integer> rightSideView(TreeNode root) {//创建存入右侧节点的数组List<Integer> res = new ArrayList<>();dfs(res, root, 0);return res;}
public void dfs(List<Integer> res, TreeNode root, int level){if(root != null){//只有在当前深度才能加入节点值if(res.size() == level){res.add(root.val);}//右视图,则先遍历右边节点,然后将其插入数组dfs(res, root.right, level + 1);//如果没有右节点,那么左节点就是右侧视图的第一个节点dfs(res, root.left, level + 1);}}
}相关文章:

Tree相关
1.树相关题目 1.1 二叉树的中序遍历(简单):递归 题目:使用中序遍历二叉树 思想:按照访问左子树——根节点——右子树的方式遍历这棵树,而在访问左子树或者右子树的时候我们按照同样的方式遍历࿰…...

git日常操作-案例
文章目录 查看远程有那些分支 查看远程有那些分支 git ls-remote --heads origin...

cmake链接.lib库
当使用CMake编写CMakeLists.txt文件来链接其他文件夹的.lib库文件时,你需要做以下几个步骤: 设置库文件路径: 使用 link_directories() 函数设置要搜索库文件的路径。例如: link_directories(${CMAKE_SOURCE_DIR}/path/to/libra…...
)
SkyWalking 部署(包含ES)
SkyWalking安装 结构 首先SkyWalking主要需要oapService、webApp、Elasticsearch(可选存储)三个,接下来讲一下这三个的安装步骤,安装过程中出现了一些细小的配置错误,导致用了快两天才弄好,麻木了&#x…...

Android学习之路(2) 设置视图
一、设置视图宽高 在Android开发中,可以使用LayoutParams类来设置视图(View)的宽度和高度。LayoutParams是一个用于布局的参数类,用于指定视图在父容器中的位置和大小。 下面是设置视图宽度和高度的示例代码: …...

SIP/VoIP之常见的视频问题
除了语音通话外,视频通话也是SIP协议通话中重要的功能,在实际应用中,经常会遇到一些视频问题,如下(以h264为例) 一、 己方未显示对方视频图像 排查方法: 查看网络抓包中有没有发给已方的视频…...
docker的服务/容器缺少vim问题
背景/问题: docker的服务/容器缺少vim问题 bash: vim: command not found 在docker的mysql服务中安装Vim 1、执行apt-get update root6d8d17e320a0:/# apt-get update问题:文件下载失败 Err:1 http://security.debian.org/debian-security buster/updates InRe…...
HCIP-OpenStack
1、OpenStack概述 OpenStack是一种云操作系统,OpenStack是虚拟机、裸金属和容器的云基础架构。可控制整个数据中心的大型计算、存储和网络资源池,所有资源都通过API或Web界面进行管理。 为什么称OpenStack是云操作系统? 云一般指云计算&…...

前端:Vue.js学习
前端:Vue.js学习 1. 第一个Vue程序2. Vue指令2.1 v-if、v-else-if、v-else2.2 v-for2.3 事件绑定 v-on:2.4 v-model 数据双向绑定2.5 v-bind 绑定属性 3. Vue组件4. Vue axios异步通信5. 计算属性6. 插槽 slots7. 自定义事件内容分发 1. 第一个Vue程序 首先把vue.js拷贝到本地…...

MySQL到Oracle快速上手
第一次做Oracle项目的时候对一些语法区别不太清楚,这里列出一些开发中发现的与MYSQL不同的点 一个用户相当于一个数据库 表空间 表空间是用于存储表、索引和其他数据库对象的逻辑存储结构。每个表空间由一个或多个数据文件组成,这些文件可以位于不同的物…...
机器人CPP编程基础-01第一个程序Hello World
很多课程先讲C/C或者一些其他编程课,称之为基础课程。然后到本科高年级进行机器人专业课学习,这样时间损失非常大,效率非常低。 C/单片机/嵌入式/ROS等这些编程基础可以合并到一门课中进行实现,这些素材已经迭代三轮以上…...
前后端分离------后端创建笔记(03)前后端对接(下)
本文章转载于【SpringBootVue】全网最简单但实用的前后端分离项目实战笔记 - 前端_大菜007的博客-CSDN博客 仅用于学习和讨论,如有侵权请联系 源码:https://gitee.com/green_vegetables/x-admin-project.git 素材:https://pan.baidu.com/s/…...

Leet code1049 最后一块石头的重量II
1049 最后一块石头的重量II 【问题描述】 有一堆石头,用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。 每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x < y。那么粉…...

Rust语法:变量,函数,控制流,struct
文章目录 变量可变与不可变变量变量与常量变量的Shadowing标量类型整数 复合类型 函数控制流if elseloop & whilefor in structstruct的定义Tuple Structstruct的方法与函数 变量 可变与不可变变量 Rust中使用let来声明变量,但是let声明的是不可变变量&#x…...

LVS简介及LVS-DR搭建
目录 一. LVS简介: 1.简介 2. LVS工作模式: 3. LVS调度算法: 4. LVS-DR集群介绍: 二.LVS-DR搭建 1.RS配置 1)两台RS,需要下载好httpd软件并准备好配置文件 2)添加虚拟IP(vip&…...

Java基础篇--日期时间类
目录 前言 Instant(时间戳)类 LocalData(日期)类 LocalTime(时间)类 LocalDataTime(日期时间)类 Duration(时间间隔)类 Period(日期间隔)类 Clock(获取时区)类 前言 在开发中经常需要处理日期和时间,Java提供…...

Vue生命周期函数 详解
以下是Vue生命周期函数的流程图和每个周期的代码详解: 流程图: beforeCreate -> created -> beforeMount -> mounted -> beforeUpdate -> updated -> beforeDestroy -> destroyed详解: beforeCreate: 触发时…...
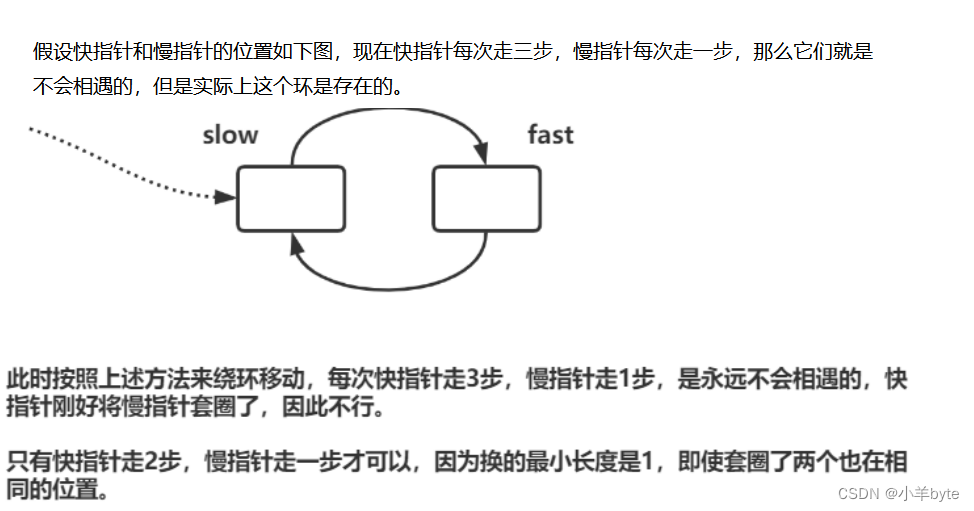
判断链表有环的证明
目录 1.问题 2.证明 3.代码实现 1.问题 给你一个链表的头节点 head ,判断链表中是否有环。 如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用…...
百度屏蔽词有哪些?其中就有移民关键词指数被屏蔽?
我是百收网SEO,点点上面的头像,欢迎关注我哦! 今日tombkeeper消息爆料:百度指数已经屏蔽“移民”等关键词指数。 大家好,我是百收网SEO商学院的狂潮微课老师,今天我们来讲解第 12 节课关键词优化难度分析…...

代码随想录day02
977.有序数组的平方 ● 力扣题目链接 ● 给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。 思路 ● 暴力排序,时间复杂度O(n nlogn) ● 使用双指针,时间复杂度O(n) …...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案
目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后,迭代器会失效,因为顺序迭代器在内存中是连续存储的,元素删除后,后续元素会前移。 但一些场景中,我们又需要在执行删除操作…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...

Spring Security 认证流程——补充
一、认证流程概述 Spring Security 的认证流程基于 过滤器链(Filter Chain),核心组件包括 UsernamePasswordAuthenticationFilter、AuthenticationManager、UserDetailsService 等。整个流程可分为以下步骤: 用户提交登录请求拦…...
