2023河南萌新联赛第(五)场:郑州轻工业大学C-数位dp
链接:登录—专业IT笔试面试备考平台_牛客网
给定一个正整数 n,你可以对 n 进行任意次(包括零次)如下操作:
- 选择 n 上的某一数位,将其删去,剩下的左右部分合并。例如 123,你可以选择删去第二位 2,得到新数 13。
在对 nnn 进行操作后,请问有多少种不同的 n,使得n 不是 3 的倍数?
由于结果可能非常大,请输出对 1000000007 取模的结果。
思路:
线性dp去求解
从前往后去枚举看有多少个时符合条件的
数组dp[i][j]记录当枚举刀第i个其中所以mod3结果是j的数j=0,1,2
然后去转移
比如1223
取123时 你的2可以从第三位和第二位的2继承过来的
dp的转移就是在前面已有的数字末尾加上一个数,如果这个数字是前面没有出过的话就在该位上加上1
第一位 1(0*2+1=1)
第二位 1,12,2(1*2+1=3)
第三位 1,12,2,12,122,22(3*2+0=6)
如果前面出现过的话你发现会和之前的产生重复就是第3位12出现了两次
我们发现第三位的12其实一次从第一位的1加上2继承下去,一次从第二位的1加上一个2继承下去
本质上就是从前一位多继承了一次,因此减去前一位的数就行了,也就是去重一下
第一位 1(0*2+1=1)
第二位 1,12,2(1*2+1=3)
第三位 1,12,2,122,22(3*2+0-1=5)
第四位1,12,2,122,22,13,123,23,1223,223,3(5*2+1=11)
最后在开3位记录是否被3整除是多少就行了
#include<iostream>
#include<algorithm>
#include<numeric>//accumulate(be,en,0)
#include<cstring>//rfind("string"),s.find(string,begin)!=s.npos,find_first _of(),find_last_of()
#include<string>//to_string(value),s.substr(int begin, int length);
#include<cstdio>
#include<cmath>
#include<vector>//res.erase(unique(res.begin(), res.end()), res.end()),reverse(q.begin(),q.end());
#include<queue>//priority_queue(big) /priority_queue<int, vector<int>, greater<int>> q(small)
#include<stack>
//#include<map>//unordered_map
#include<set>//iterator,insert(),erase(),lower(>=)/upper_bound(>)(value)/find()return end()
#include<unordered_map>
#include<unordered_set>
#include<bitset>//size,count(size of 1),reset(to 0),any(have 1?)
//#include<ext/pb_ds/assoc_container.hpp>//gp_hash_table
//#include<ext/pb_ds/hash_policy.hpp>
//using namespace __gnu_pbds;
#define int long long//__int128 2^127-1(GCC)
#define PII pair<int,int>
using namespace std;
const int inf = 0x3f3f3f3f3f3f3f3f, N = 2e5 + 5, mod = 1e9 + 7;
int dp[N][3];
signed main()
{ios_base::sync_with_stdio(0); cin.tie(0), cout.tie(0);string s;cin >> s;s = ' ' + s;int n = s.length();int pre[10] = { 1 };dp[0][0] = 1;for (int i = 1; i < n; i++) {int x = s[i] - '0';int m = pre[x];for (int j = 0; j < 3; j++)dp[i][(j + x) % 3] = (dp[i - 1][(j + x) % 3] + dp[i - 1][j]) % mod;if (m){for (int j = 0; j < 3; j++)dp[i][(j + x) % 3] = (dp[i][(j + x) % 3] + mod - dp[m - 1][j]) % mod;}pre[x] = i;}cout << (dp[n - 1][1] + dp[n - 1][2]) % mod << '\n';}相关文章:
场:郑州轻工业大学C-数位dp)
2023河南萌新联赛第(五)场:郑州轻工业大学C-数位dp
链接:登录—专业IT笔试面试备考平台_牛客网 给定一个正整数 n,你可以对 n 进行任意次(包括零次)如下操作: 选择 n 上的某一数位,将其删去,剩下的左右部分合并。例如 123,你可以选择…...

找不到mfc140u.dll怎么办?mfc140u.dll丢失怎样修复?简单三招搞定
最近我遇到了一个问题,发现我的电脑上出现了mfc140u.dll文件丢失的错误提示。这个错误导致一些应用程序无法正常运行,让我感到非常困扰。经过一番研究和尝试,我终于成功修复了这个问题,并从中总结出了一些心得。 mfc140u.dll丢失原…...
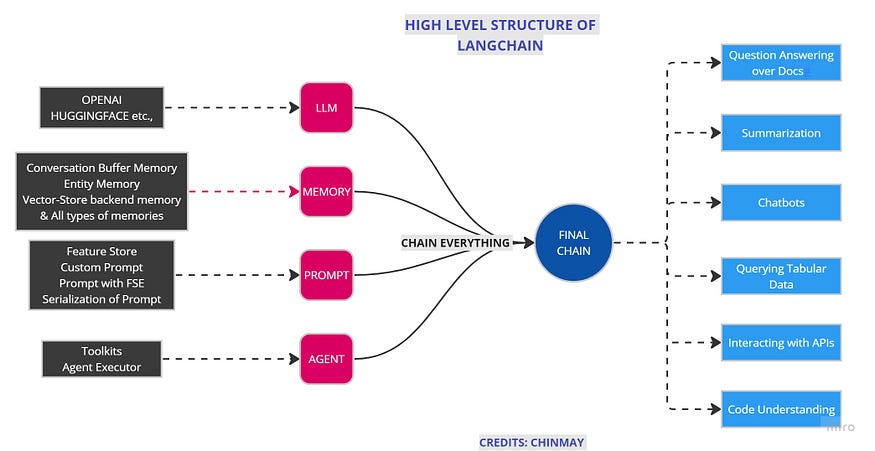
了解 Langchain️是个啥?:第 1 部分
一、说明 在日常生活中,我们主要致力于构建端到端的应用程序。我们可以使用许多自动 ML 平台和 CI/CD 管道来自动化 ml 管道。我们还有像Roboflow和Andrew N.G.的登陆AI这样的工具来自动化或创建端到端的计算机视觉应用程序。 如果我们想在OpenAI或拥抱脸的帮助下创…...
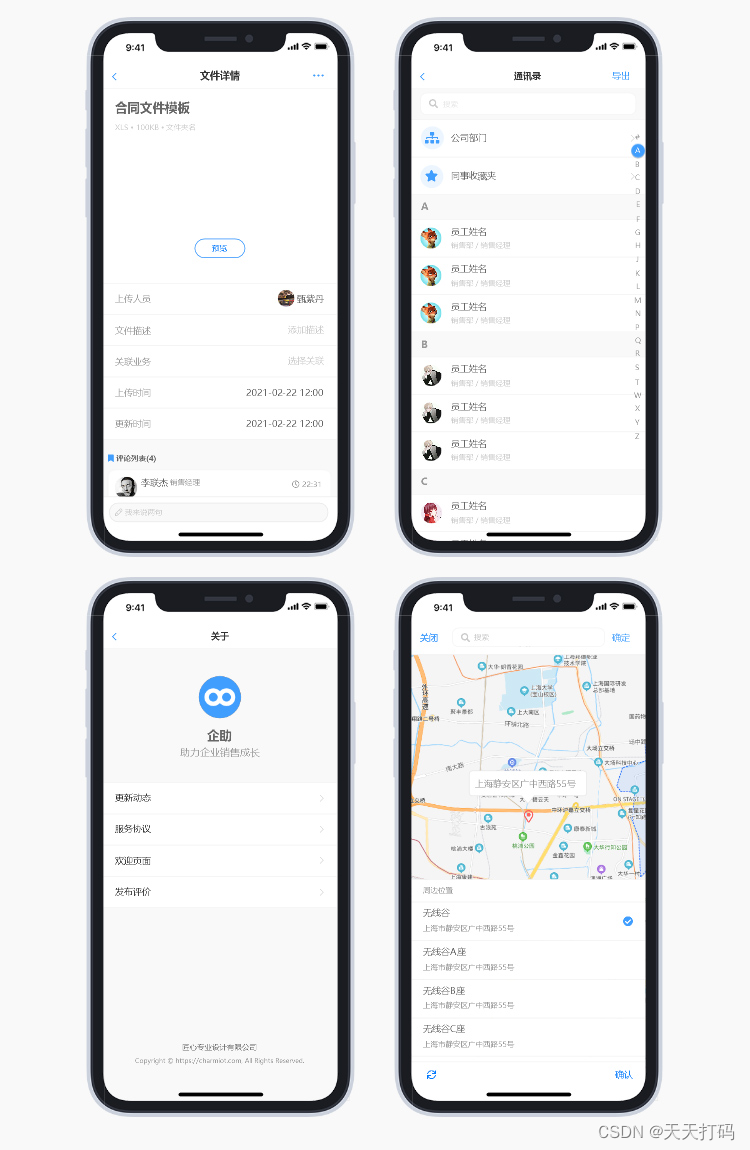
Axure RP移动端高保真CRM办公客户管理系统原型模板及元件库
Axure RP移动端高保真CRM办公客户管理系统原型模板及元件库,一套典型的移动端办公工具型APP Axure RP原型模板,可根据实际的产品需求进行扩展,也可以作为移动端原型设计的参考案例。为提升本作品参考价值,在模板设计过程中尽量追求…...

【JAVA】我们常常谈到的方法是指什么?
个人主页:【😊个人主页】 系列专栏:【❤️初识JAVA】 文章目录 前言方法方法的分类方法的定义方法调用方法重载 前言 在之前的文章中我们总是会介绍到类中的各式各样的方法,也许在应用中我们对它已经有了初步的了解,今…...

今天来给大家聊一聊什么是Hierarchical-CTC模型
随着人工智能领域的不断发展,语音识别技术在日常生活和工业应用中扮演着越来越重要的角色。为了提高识别准确性和效率,研究人员不断探索新的模型和算法。在这个领域中,Hierarchical-CTC模型引起了广泛的关注和兴趣。本文将介绍什么是Hierarch…...

cout还是printf?C++教程 - How to C++系列专栏第4篇
关于专栏 这个专栏是优质的C教程专栏,如果你还没看过第一篇,点击这里去第0篇 本专栏一致使用操作系统:macOS Ventura,代码编辑器:CLion,C编译器:Clang 感谢一路相伴的朋友们,感谢…...
Linux NTP原理及配置使用
一、NTP简介 1.NTP简介 NTP(Network Time Protocol,网络时间协议)是用来使网络中的各个计算机时间同步的一种协议。它的用途是把计算机的时钟同步到世界协调时UTC,其精度在局域网内可达0.1ms,在互联网上绝大多数的…...

SAP系统是什么呢?它有哪些优势?
SAP系统是全球知名的企业资源规划(ERP)解决方案供应商。它集成了财务、供应链管理、人力资源管理、销售和客户关系管理等多个功能模块,为企业提供全面、集成的管理体验。SAP系统已成为各行各业企业管理的智慧选择,极大地提升了管理…...
)
js数组学习(ES6+)
文章目录 js(ES6)数组学习1.Array.prototype.forEach(fn)2.Array.prototype.map(fn)3.Array.prototype.filter(fn)4.Array.prototype.reduce(fn)5.Array.prototype.some(fn) every6.Array.prototype.find(fn)7.Array.prototype.includes(item) js(ES6)数组学习 1.Array.protot…...
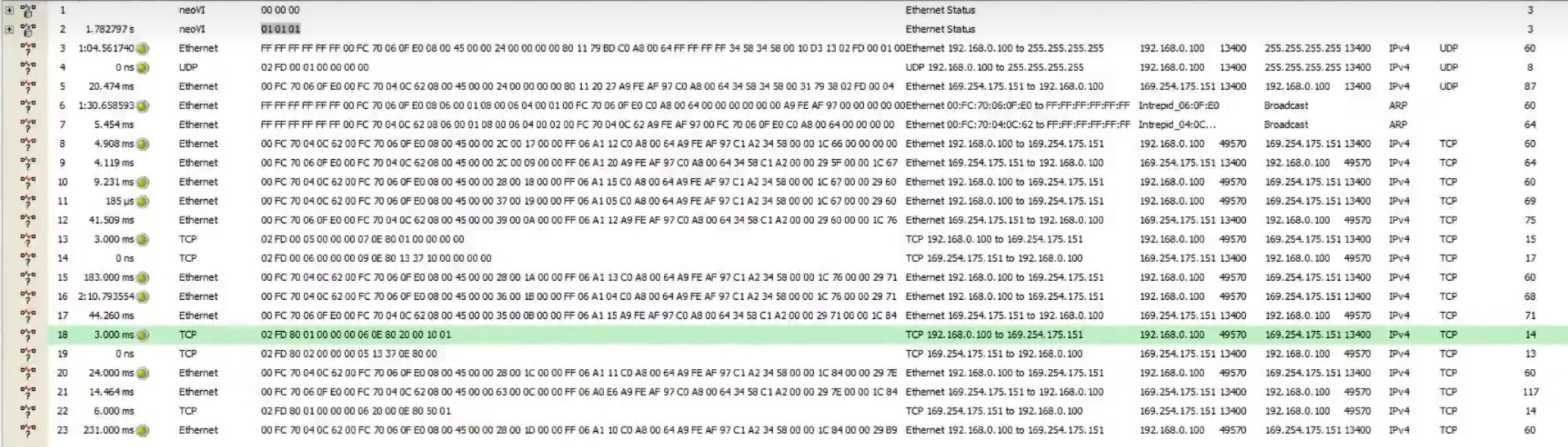
DoIP诊断入门
简介 DoIP(Diagnosis over Internet Protocol)是一种用于车辆诊断的网络通信协议。它基于现代互联网技术,允许通过以太网或IP网络进行车辆诊断和通信。 DoIP的背景是现代车辆中使用的电子控制单元(ECU)数量不断增加&…...

Amazon CloudFront 部署小指南(五)- 使用 Amazon 边缘技术优化游戏内资源更新发布...
内容简介 游戏内资源包括玩家的装备/弹药/材料等素材,对游戏内资源的发布和更新是游戏运营商的一个常规业务流程,使用频率会十分高,所以游戏运营商希望该流程可以做到简化和可控。针对这个需求,我们设计了 3 个架构,面…...

undefined reference to `dlopen‘ ‘SSL_library_init‘ `X509_certificate_type‘
使用Crow的时候需要注意crow依赖asio依赖OpenSSL,asio要求1.22以上版本,我使用的是1.26.0; 这个版本的asio要求OpenSSL是1.0.2,其他版本我得机器上编不过,ubuntu上默认带的OpenSSL是1.1.1; 所以我下载了OPENSSL1.2.0重…...

DHCPv6之GitHub项目Android侧验证
一、adb里面安装busybox 1、下载busybox 下载网址:Index of /downloads/binaries/1.21.1 (busybox.net),目前最新是1.21.1版本 根据项目选择busybox-armv7l ,右键另存为下载到本地目录,下载后去掉文件的后缀名,变成如…...

简单易懂的 Postman Runner 参数自增教程
目录 什么是 Postman Runner? Postman Runner 如何实现参数自增? 步骤一:设置全局参数 步骤二:将全局参数带入请求参数 步骤三:实现参数自增 资料获取方法 什么是 Postman Runner? Postman Runner 是…...
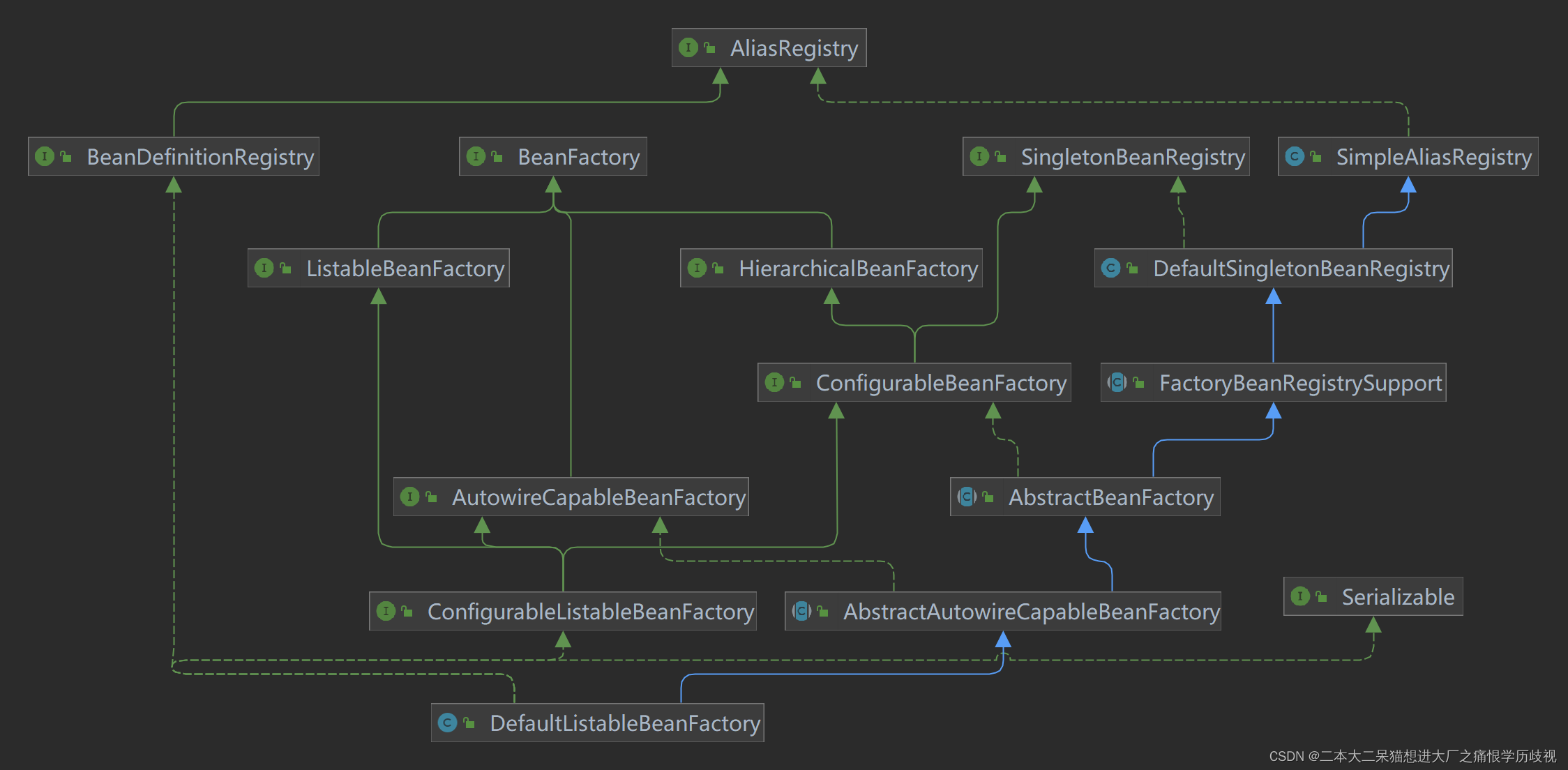
BeanFactory与Applicationcontext(1)
BeanFactory是接口,提供了IOC容器最基本的形式,给具体的IOC容器的实现提供了规范。BeanFactory是spring的“心脏”,核心容器,它也是Applicationcontext的父接口。 BeanFactory实质上并未提供过多的方法,spring容器的I…...

C++初阶之模板深化讲解
模板深化讲解 非类型模板模板的特化1.函数模板特化2.类模板特化 模板分离编译1.什么是分离编译2.模板的分离编译 模板总结 非类型模板 非类型模板(Non-Type Template)是 C 中的一种模板形式,它允许你在模板中传递除了类型以外的其他值&#x…...

Redis数据结构——整数集合
定义 整数集合是集合的实现方式之一,当一个集合只包含整数值元素时,并且这个集合的元素数量不多时,Redis就会使用整数集合作为集合的底层实现。 整数集合就是存放整数的一个数组,整数集合的结构体定义: typeof struc…...

背上大书包准备面试之CSS篇
目录 H5 新特性 css3新特性? 为什么要初始化css样式? 浏览器兼容性问题? css sprites(css精灵图)? css盒模型是什么样的? 页面中一个块元素的宽度包含了盒模型中的哪些部分?…...

linux系列基本介绍
虽然我们常说Linux操作系统,这种叫法是不正确的,严格意义上讲,Linux并不是操作系统,而是属于操作系统的一个内核,inux内核提供了操作系统的核心功能,如进程管理、内存管理、文件系统等。 Linux有很多不同的…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...
