DP——动态规划
DP——动态规划
- 动态规划算法
- 动态规划的一般步骤
- 特殊DP——背包
- 0-1背包问题
- 完全背包问题
- 总结
动态规划算法
当涉及到解决具有重叠子问题的优化问题时,动态规划是一种常用的算法技术。它通过将问题分解为一系列重叠子问题,并使用递归或迭代的方式来解决这些子问题,最终得到问题的最优解。
动态规划的核心思想是将原始问题分解为更小的子问题,并通过解决这些子问题来构建原始问题的解。在解决子问题时,动态规划会将子问题的解保存起来,以便在需要时进行重复使用,从而避免了重复计算。
动态规划的一般步骤
要实现动态规划算法,可以按照以下步骤进行:
确定问题的状态:首先,需要确定问题的状态,这些状态应该能够唯一地表示问题的子问题。状态可以是一个或多个变量的组合,可以是一个数字、一个数组、一个矩阵等,具体取决于问题的性质。
-
定义状态转移方程:根据问题的定义和性质,确定问题的状态之间的转移关系,即如何从一个状态转移到另一个状态。这个方程通常是基于递推关系或者最优子结构性质来定义的。
-
确定初始条件:确定最小子问题的解,即初始状态的值。这些初始条件是问题的边界条件,用于开始递推计算。
-
确定计算顺序:确定计算子问题解的顺序,通常是从最小子问题开始,逐步计算更大的子问题,直到计算出原始问题的解。这个顺序可以是自顶向下的递归方式,也可以是自底向上的迭代方式。
-
计算最优解:根据状态转移方程和初始条件,计算出原始问题的最优解。可以使用递归或迭代的方式进行计算。
-
构建最优解:根据计算出的最优解和保存的中间结果,构建出原始问题的最优解。这一步通常是通过回溯或者追踪中间结果的方式进行。
需要注意的是,动态规划算法的实现可以使用递归或迭代的方式,具体取决于问题的性质和计算效率的要求。在实现过程中,可以使用数组、矩阵或者哈希表等数据结构来保存中间结果,以便在需要时进行查找和使用。
特殊DP——背包
背包问题是一个经典的优化问题,它可以通过动态规划算法进行求解。在背包问题中,有一个背包和一组物品,每个物品都有自己的重量和价值。目标是选择一些物品放入背包中,使得放入背包的物品总重量不超过背包的容量,同时使得放入背包的物品总价值最大化。
背包问题可以分为两种类型:0-1背包问题和无限背包问题。
0-1背包问题
每个物品只能选择放入背包一次或不放入。即物品的选择是一个二进制的决策。这种情况下,动态规划的状态可以定义为“在前i个物品中,背包容量为j时的最大价值”。状态转移方程可以表示为: dp[i][j] = max(dp[i-1][j], dp[i-1][j-w[i]] + v[i]) 其中,dp[i][j]表示前i个物品中,背包容量为j时的最大价值,w[i]表示第i个物品的重量,v[i]表示第i个物品的价值。
完全背包问题
每个物品可以选择放入背包多次,即物品的选择是一个非负整数。这种情况下,动态规划的状态可以定义为“在前i个物品中,背包容量为j时的最大价值”。状态转移方程可以表示为: dp[i][j] = max(dp[i-1][j], dp[i][j-w[i]] + v[i]) 其中,dp[i][j]表示前i个物品中,背包容量为j时的最大价值,w[i]表示第i个物品的重量,v[i]表示第i个物品的价值。
动态规划算法的实现步骤如下:
-
定义问题的状态:确定状态的定义,即dp数组的含义和维度。
-
初始化:根据问题的定义,初始化dp数组的初始值。
-
状态转移:根据状态转移方程,使用循环遍历物品和背包容量,更新dp数组的值。
-
返回结果:根据问题的定义,从dp数组中获取最优解的值。
-
可选的步骤:如果需要构建最优解的具体物品组合,可以使用额外的数据结构(如二维数组或哈希表)来保存选择的信息,然后根据这些信息构建最优解。
通过以上步骤,可以使用动态规划算法解决背包问题,并得到最优的物品选择方案和总价值。
总结
总结起来,实现动态规划算法的关键在于确定问题的状态和状态转移方程,并按照计算顺序进行递推或迭代计算,最终得到原始问题的最优解。
相关文章:

DP——动态规划
DP——动态规划 动态规划算法动态规划的一般步骤特殊DP——背包0-1背包问题完全背包问题 总结 动态规划算法 当涉及到解决具有重叠子问题的优化问题时,动态规划是一种常用的算法技术。它通过将问题分解为一系列重叠子问题,并使用递归或迭代的方式来解决…...
【Windows 11】安装 Android子系统 和 Linux子系统
本文使用电脑系统: 文章目录 一、安卓子系统1.1 安装 WSA1.2 使用 二、Linux子系统2.1 安装 WSL 以及WSL 相关概念2.2 安装一个Linux发行版2.21 从Microsoft Store 安装2.22 用命令安装 2.23 拓展 三、拓展3.1 存储位置3.2 虚拟化技术3.3 Windows 虚拟内存3.3 wsl …...
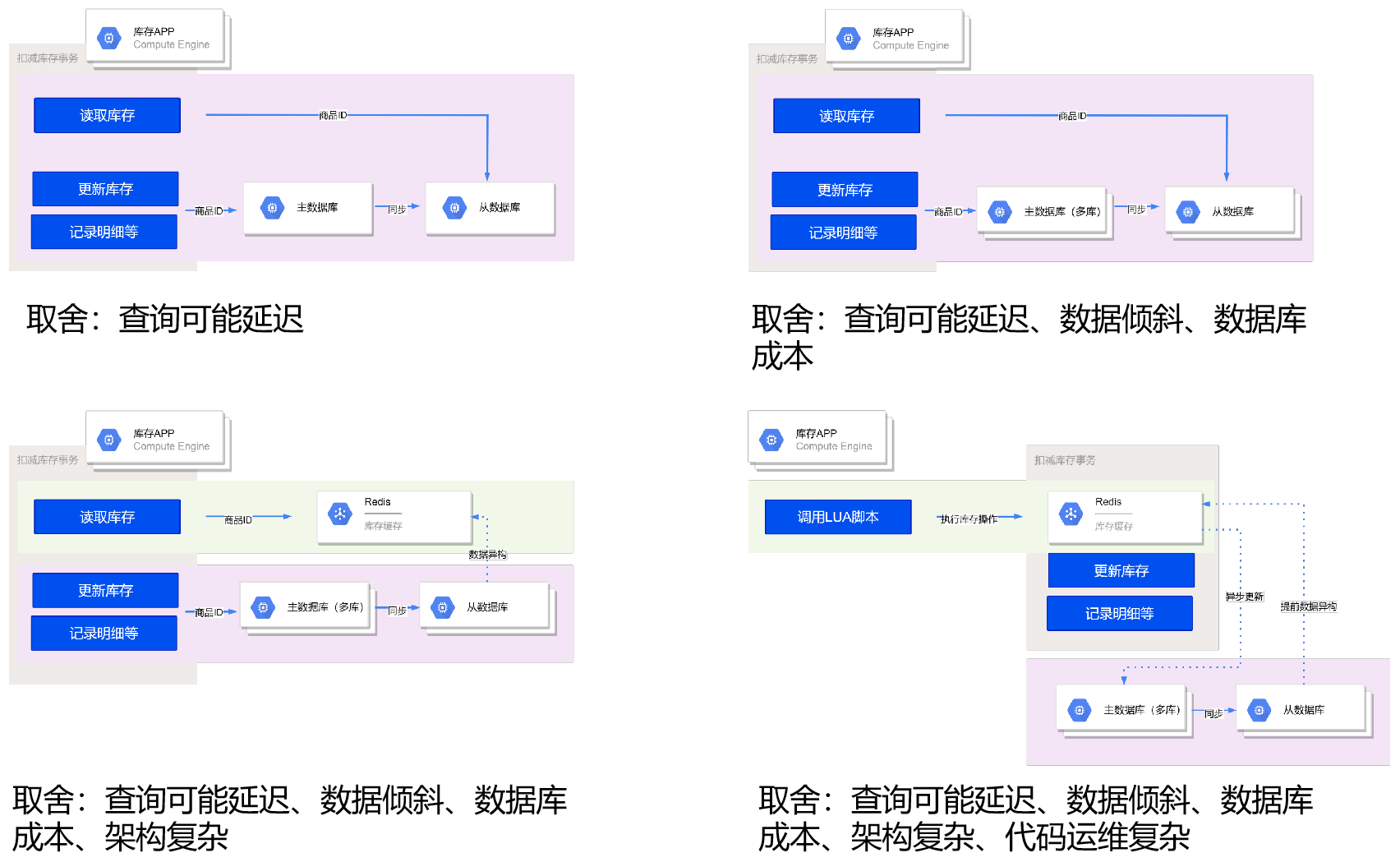
秒杀库存解决方案
电商系统中秒杀是一种常见的业务场景需求,其中核心设计之一就是如何扣减库存。本篇主要分享一些常见库存扣减技术方案,库存扣减设计选择并非一味追求性能更佳,更多的应该考虑根据实际情况来进行架构取舍。在商品购买的过程中,库存…...

[免费在线] 将 PDF 转换为 Excel 或 Excel 转换为 PDF | 5 工具
有了免费的在线 PDF 转换器,您可以轻松免费在线将 PDF 转换为 Excel 或 Excel 转换为 PDF。这篇文章为您筛选了 5 个最常用的工具。要从存储介质恢复错误删除或丢失的 PDF 文档、Excel 电子表格、Word 文件或任何其他文件,您可以使用免费的数据恢复程序 …...
PLC求解弹簧质量模型微分方程数值解(RK4梯形图程序)
微分方程的数值求解,属于数学分析类课程涉及的内容。大家可以参看相关书籍对Runge-Kutta法的介绍,弹簧质量阻尼模型详细的微分方程介绍可以查看下面文章,链接如下: 弹簧质量阻尼系统前馈PID位置控制(PLC闭环仿真SCL+ST代码)_RXXW_Dor的博客-CSDN博客带前馈控制的博途PID程…...

CSDN编程题-每日一练(2023-08-14)
CSDN编程题-每日一练(2023-08-14) 一、题目名称:小股炒股二、题目名称:王子闯闸门三、题目名称:圆小艺 一、题目名称:小股炒股 时间限制:1000ms内存限制:256M 题目描述: …...

【SA8295P 源码分析】69 - Android 侧添加支持 busybox telnetd 服务
【SA8295P 源码分析】69 - Android 侧添加支持 busybox telnetd 服务 一、下载 busybox-1.36.1.tar.bz2 源码包二、编译 busybox 源码三、将编译后的 busybox 打包编入Android 镜像中系列文章汇总见:《【SA8295P 源码分析】00 - 系列文章链接汇总》 本文链接:《【SA8295P 源码…...

OpenCV图像处理——模版匹配和霍夫变换
目录 模版匹配原理实现 霍夫变换霍夫线检测 模版匹配 原理 实现 rescv.matchTemplate(img,template,method)import numpy as np import cv2 as cv import matplotlib.pyplot as pltimgcv.imread(./汪学长的随堂资料/6/模板匹配/lena.jpg) templatecv.imread(./汪学长的随堂资…...
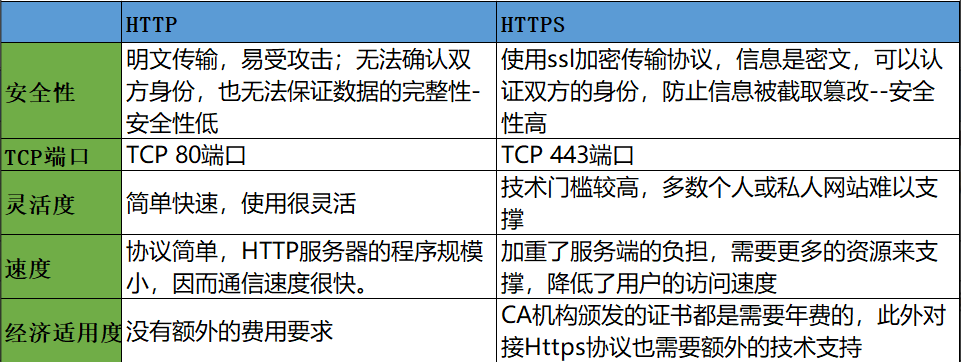
面试官的几句话,差点让我挂在HTTPS上
♥ 前 言 作为软件测试,大家都知道一些常用的网络协议是我们必须要了解和掌握的,比如 HTTP 协议,HTTPS 协议就是两个使用非常广泛的协议,所以也是面试官问的面试的时候问的比较多的两个协议;而且因为这两个协议有相…...

C语言char**,char*,char s[]赋值
目录 前言 赋值方法 char s[]: char* char** 问题 修改字符串常量 前言 char**,char*,char s[]赋值的方式是不同的,当你搞混的时候,系统会报出段错误(Segmentation Fault),所…...

一、Kubernetes介绍与集群架构
Kubernetes介绍与集群架构 一、认识容器编排工具 docker machine 主要用于准备docker host现已弃用建议使用docker desktop docker compose Compose 是一个用于定义和运行多容器 Docker 应用程序的工具。使用 Compose,您可以使用 YAML 文件来配置应用程序的服务。…...
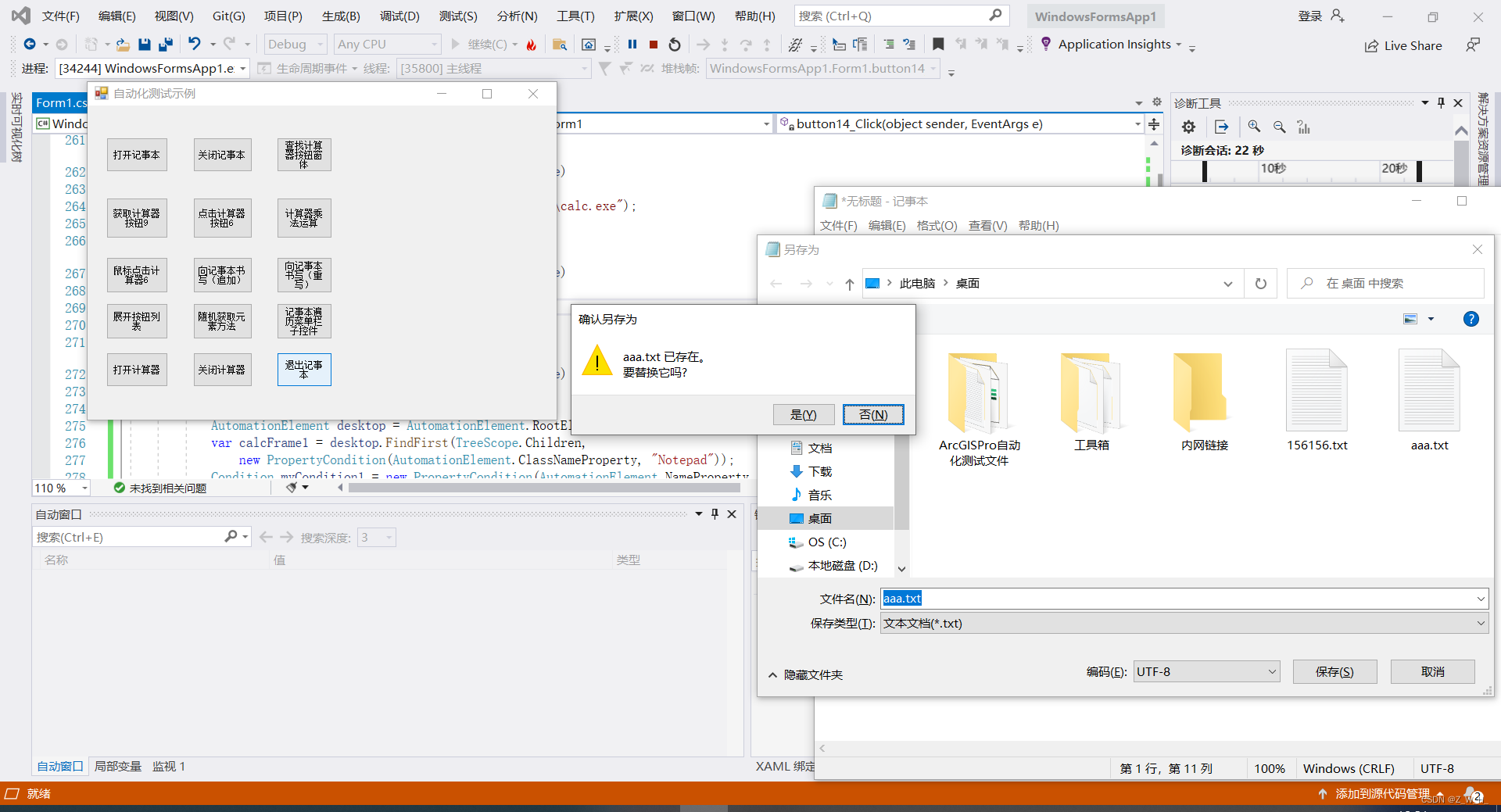
基于C#UI Automation自动化测试
步骤 UI Automation 只适用于,标准的win32和 WPF程序 需要添加对UIAutomationClient、 UIAutomationProvider、 UIAutomationTypes的引用 代码 using System; using System.Collections.Generic; using System.ComponentModel; using System.Data; using System.D…...

深入了解Linux运维的重要性与最佳实践
Linux作为开源操作系统的代表,在企业级环境中的应用越来越广泛。而在保障Linux系统的正常运行和管理方面,Linux运维显得尤为关键。本文将介绍Linux运维的重要性以及一些最佳实践,帮助读者更好地了解和掌握Linux系统的运维技巧。 首先…...

90 | Python人工智能篇 —— 深度学习算法 Keras基于卷积神经网络的情感分类
情感分类是自然语言处理(NLP)领域的一个重要任务,它旨在将文本划分为积极、消极或中性等不同情感类别。深度学习技术,尤其是卷积神经网络(CNN),在情感分类任务中取得了显著的成果。Keras作为一个高级的深度学习框架,提供了便捷易用的工具来构建和训练情感分类模型。 文…...
-[记忆的类型Ⅲ])
自然语言处理从入门到应用——LangChain:记忆(Memory)-[记忆的类型Ⅲ]
分类目录:《自然语言处理从入门到应用》总目录 对话令牌缓冲存储器ConversationTokenBufferMemory ConversationTokenBufferMemory在内存中保留了最近的一些对话交互,并使用标记长度来确定何时刷新交互,而不是交互数量。 from langchain.me…...

【ARM 嵌入式 编译系列 10.3 -- GNU elfutils 工具小结】
文章目录 什么是 GNU elfutils?GNU elfutils 常用工具有哪些?objcopy 常用参数有哪些?GNU binutils和GNU elfutils区别是什么? 上篇文章:ARM 嵌入式 编译系列 10.2 – 符号表与可执行程序分离详细讲解 什么是 GNU elfu…...

黑马项目一阶段面试 项目介绍篇
我完成了一个外卖项目,名叫苍穹外卖,是跟着黑马程序员的课程来自己动手写的。 项目基本实现了外卖客户端、商家端的后端完整业务。 商家端分为员工管理、文件上传、菜品管理、分类管理、套餐管理、店铺营业状态、订单下单派送等的管理、数据统计等&…...

重构内置类Function原型上的call方法
重构内置类Function原型上的call方法 // > 重构内置类Function原型上的call方法 ~(function () {/*** call: 改变函数中的this指向* params* context 可以不传递,传递必须是引用类型的值,因为后面要给它加 fn 属性**/function myCall(context) {/…...

Nginx之lnmp架构
目录 一.什么是LNMP二.LNMP环境搭建1.Nginx的搭建2.安装php3.安装数据库4.测试Nginx与PHP的连接5.测试PHP连接数据库 一.什么是LNMP LNMP是一套技术的组合,Llinux,Nnginx,Mmysql,Pphp 首先Nginx服务是不能处理动态资源请求&…...
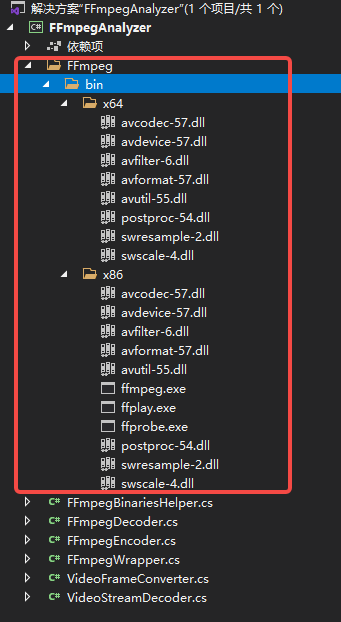
C# 使用FFmpeg.Autogen对byte[]进行编解码
C# 使用FFmpeg.Autogen对byte[]进行编解码,参考:https://github.com/vanjoge/CSharpVideoDemo 入口调用类: using System; using System.IO; using System.Drawing; using System.Runtime.InteropServices; using FFmpeg.AutoGen;namespace F…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...
