第三章 图论 No.12欧拉回路与欧拉路径
文章目录
- 定义
- 欧拉路径的性质:1123. 铲雪车
- 边编号输出欧拉路径:1184. 欧拉回路
- 点编号字典序最小输出欧拉路径:1124. 骑马修栅栏
- 并查集判断有向图是否存在欧拉路径:1185. 单词游戏
定义
小学一笔画问题,每条边只经过一次
判断图是否存在欧拉回路:判断图是否连通(存在孤立边),再根据有向/无向具体判断
对于无向图来说,欧拉路径中,起点和终点的度数为奇数,中间点的度数为偶数
起点和终点:开始和结束时必须经过一条边,其余情况为:从一条边进入,再从另一条边离开,即度数为1 + 2 * n
中间点:一条边进入,一条边离开,度数为2 * n
欧拉回路中,所有点的度数为偶数

七桥问题中,由于每个点的度数为奇数,所以不可能存在欧拉路径
以下结论直接记:

欧拉路径的性质:1123. 铲雪车
1123. 铲雪车 - AcWing题库
根据题意,所有的街道都是双向,说明这张图是一张有向图。每个城市都连接了街道,说明这张图是连通图。将每个城市看成点,那么每个点的入度都等于出度,这张图存在欧拉回路,所以无论如何,我们都有一条路径,能够不重复不遗漏的遍历所有的边,而这道题要求时间(最短路径),我们不需要算出具体的欧拉回路,以为欧拉回路的距离一定是所有路径之和,只要根据题意将路径转换成时间即可
#include <iostream>
#include <cmath>
using namespace std;int main()
{double x1, y1, x2, y2;scanf("%lf%lf", &x1, &y1);double sum = 0;while (~scanf("%lf%lf%lf%lf", &x1, &y1, &x2, &y2)){double x = x1 - x2, y = y1 - y2;sum += sqrt(x * x + y * y) * 2;}int mte = round(sum / 1000 * 60 / 20);int hour = mte / 60;mte %= 60;printf("%d:%02d\n", hour, mte);return 0;
}
debug:距离要乘2,每条道路都是双向的
边编号输出欧拉路径:1184. 欧拉回路
1184. 欧拉回路 - AcWing题库
欧拉路径的板子:
若一张图存在欧拉路径,可以用dfs递归完所有的边,在dfs回溯时记录边的编号到数组中,最后逆着输出该数组即可
用uesd数组标记已经遍历过的边,同时每遍历完一条边就删除这条边,防止重复遍历
其实有向图不需要使用used数组,只要删除遍历完的边即可
开uesd数组是因为无向图,由于我们用单链表存储边,虽然可以删除当前正在遍历的边,但是在无向图中,删除反向边比较麻烦,所以这里用uesd数组标记反向边,保证每条边只会遍历一次
需要注意,不要遍历孤立点,若图中存在欧拉路径,孤立点不会影响欧拉路径
还要注意,这题的无向图的欧拉回路中,若边的方向与输入给定的方向不同,那么需要输出编号的负数
#include <iostream>
#include <cstring>
using namespace std;const int N = 1e5 + 10, M = 4e5 + 10;
int h[N], e[M], ne[M], idx;
int din[N], dout[N];
int ans[M / 2], cnt;
bool used[M];
int type, n, m;void add(int x, int y)
{e[idx] = y, ne[idx] = h[x], h[x] = idx ++ ;
}void dfs(int x)
{for (int &i = h[x]; i != -1;){if (used[i]){i = ne[i];continue;}int t; // 当前边的编号used[i] = true;if (type == 1) {used[i ^ 1] = true;t = i / 2 + 1;if (i & 1) t = -t;}else t = i + 1;int y = e[i];i = ne[i];dfs(y);ans[++ cnt] = t;}
}int main()
{memset(h, -1, sizeof(h));cin >> type >> n >> m;int x, y;for (int i = 0; i < m; ++ i ){scanf("%d%d", &x, &y);add(x, y);if (type == 1) add(y, x);din[y] ++ , dout[x] ++ ;}if (type == 1)for (int i = 1; i <= n; ++ i )if ((din[i] + dout[i]) % 2){puts("NO");return 0;}if (type == 2)for (int i = 1; i <= n; ++ i )if (din[i] != dout[i]){puts("NO");return 0;}for (int i = 1; i <= n; ++ i )if (h[i] != -1){dfs(i);break;}if (cnt < m){puts("NO");return 0;}puts("YES");for (int i = m; i ; -- i )printf("%d ", ans[i]);puts("");return 0;
}
要特别注意:求欧拉路径后,必须要判断这条路径是否遍历了所有的边
点编号字典序最小输出欧拉路径:1124. 骑马修栅栏
1124. 骑马修栅栏 - AcWing题库

题目要求按照点的编号最小字典序输出欧拉路径,可以dfs(x)时,可以先遍历与x相连的编号较小的点,那么与x相连的点中,相较于编号较大的点,编号较小的点将被存储到序列的靠后位置,逆序后编号较小的点位于序列的靠前位置,满足最小字典序
为什么不使用邻接表存储图?
用邻接表存储图时,选择编号较小的点会比较麻烦,需要对单链表中的元素进行排序
用邻接矩阵存储图,直接按照下标从小到大dfs与x相连的点即可
需要注意的是,题目可能存在重边,通常邻接矩阵存储边权的最小/大值,但是这题需要存储两点间边的数量,以保证之后的dfs中每条边都被遍历
还有一点:图是无向图,但题目没有说存在欧拉回路还是欧拉路径,如果存在欧拉路径,那么起点和终点的度数为奇数。如果存在欧拉回路,那么所有点的度数为偶数
所以dfs之前需要找度数为奇数的点,若找到,说明该图一定存在欧拉路径,可能不存在欧拉回路。此时从度数为偶数的点dfs将无法正确遍历欧拉路径,只有存在欧拉回路的情况下,才能从度数为偶数的点dfs
并且,1不是最小的点编号,点编号范围在1~500,所以要找到一个度数非0的点编号,再找是否存在欧拉路径,最后再dfs
由于使用邻接矩阵存储无向图,所以不需要开used数组,每次遍历一条边,能够很简单地删除这条边和其反向边
#include <iostream>
using namespace std;const int N = 510, M = 2100;
int g[N][N], d[N];
int ans[M], cnt;
int n, m;void dfs(int x)
{for (int y = 1; y < N; ++ y ){if (g[x][y]){g[x][y] -- , g[y][x] --;dfs(y);}}ans[ ++ cnt ] = x;
}int main()
{scanf("%d", &m);int x, y;for (int i = 0; i < m; ++ i ){scanf("%d%d", &x, &y);g[x][y] ++ , g[y][x] ++ ;d[x] ++ , d[y] ++ ;}int start = 1;while (!d[start]) start ++ ;for (int i = start; i < N; ++ i )if (d[i] % 2){start = i;break;}dfs(start);for (int i = cnt; i; -- i ) printf("%d\n", ans[i]);return 0;
}
并查集判断有向图是否存在欧拉路径:1185. 单词游戏
1185. 单词游戏 - AcWing题库
建图方式:以单词的第一个字母或最后一个字母为点,从前往后建一条有向边
问题转换成:判断有向图中是否存在欧拉路径,当然可能也是欧拉回路
由于不需要找出具体的欧拉路径,所以可以不用dfs,只要满足所有点的入度等于出度(欧拉回路),或者(欧拉路径)入度比出度多1(终点),出度比入度多1(起点)
该图就存在欧拉路径,当然,还需要判断是否有孤立边,由于这题特殊的建图方式,若存在一个单词是孤立的,那么在图中表现为两点一边的孤立
判断是否存在孤立边,可以dfs跑一遍欧拉路径,判断边数是否小于图的边数
但是可以用更简单的并查集,维护每个点属于的集合,建完图后,一旦出现两点属于不同集合,那么图中一定存在孤立边(因为该图中的点一定连接着一条边,所以点孤立=边孤立)
#include <iostream>
#include <cstring>
using namespace std;const int N = 30, M = 1e5 + 10;
bool st[N];
int din[N], dout[N];
int p[N];
int T, m;int find(int x)
{if (x != p[x]) p[x] = find(p[x]);return p[x];
}int main()
{scanf("%d", &T);while (T -- ){memset(st, false, sizeof(st));memset(din, 0, sizeof(din));memset(dout, 0, sizeof(dout));for (int i = 0; i < 26; ++ i ) p[i] = i;char str[1010];scanf("%d", &m);for (int i = 0; i < m; ++ i ){scanf("%s", str);int len = strlen(str);int x = str[0] - 'a', y = str[len - 1] - 'a';st[x] = st[y] = true;din[y] ++ , dout[x] ++ ;p[find(x)] = p[find(y)];}int start = 0, end = 0; // 起点和终点的数量bool flag = true;for (int i = 0; i < 26; ++ i )if (din[i] != dout[i]){if (din[i] + 1 == dout[i]) end ++ ;else if (din[i] == dout[i] + 1) start ++ ;else {flag = false;break;}}if (flag && !((!start && !end) || (start == 1 && end == 1))) // 起点数和终点数不正确flag = false;// 判断是否存在孤立边int t = -1;for (int i = 0; i < 26; ++ i )if (st[i]){if (t == -1) t = find(i);else if (t != find(i)){flag = false;break;}}if (flag) puts("Ordering is possible.");else puts("The door cannot be opened.");}return 0;
}
相关文章:

第三章 图论 No.12欧拉回路与欧拉路径
文章目录 定义欧拉路径的性质:1123. 铲雪车边编号输出欧拉路径:1184. 欧拉回路点编号字典序最小输出欧拉路径:1124. 骑马修栅栏并查集判断有向图是否存在欧拉路径:1185. 单词游戏 定义 小学一笔画问题,每条边只经过一次…...
)
kubernetes(二)
文章目录 1. kubernetes常用资源1.1 deployment资源1.2 deployment升级和回滚1.3 tomcat连接mysql1.4 wordpress 2. kubernetes的附加组件2.1 kubernetes集群配置dns服务2.2 kubernetes的dns配置文件2.3 namespace命名空间2.4 kubernetes健康检查2.4.1 健康检查livenessprobo2.…...

MATLAB算法实战应用案例精讲-【深度学习】预训练模型ELECTRAPerformer
目录 ELECTRA 1.介绍 2.模型结构 2.1 Replaced Token Detection 2.2 权重共享 2.3 更小的生成器 3...
微服务05-Sentinel流量防卫兵
随着微服务的流行,服务和服务之间的稳定性变得越来越重要。Sentinel 是面向分布式、多语言异构化服务架构的流量治理组件,主要以 流量 为切入点,从流量路由、流量控制、流量整形、熔断降级、系统自适应过载保护、热点流量防护等多个维度来帮助开发者保障微服务的稳定性。 S…...
【考研数学】概率论与数理统计 | 第一章——随机事件与概率(1)
文章目录 一、随机试验与随机事件1.1 随机试验1.2 样本空间1.3 随机事件 二、事件的运算与关系2.1 事件的运算2.2 事件的关系2.3 事件运算的性质 三、概率的公理化定义与概率的基本性质3.1 概率的公理化定义3.2 概率的基本性质 写在最后 一、随机试验与随机事件 1.1 随机试验 …...
【设计模式】建造者模式
建造者模式(Builder Pattern)使用多个简单的对象一步一步构建成一个复杂的对象。这种类型的设计模式属于创建型模式,它提供了一种创建对象的最佳方式。 一个 Builder 类会一步一步构造最终的对象。该 Builder 类是独立于其他对象的。 介绍 …...

网络安全---正则回溯
目录 一、题目引入 二、举出回溯例子进行分析 第一步: 正则往前匹配 第二步:匹配到头 第三步:往回匹配 第四步:直到分号结束 (匹配上) 原因: 三、进入正题一(分析题型&#…...

压测秒杀场景常见问题
很多人在做秒杀场景的压测时,经常出现以下两个问题: 1,用自己的笔记本电脑瞬间发起1000个请求 2,没有使用虚拟ip(发起的请求都是同样的一个ip) 其实现在很多人在做秒杀压测的时候,都会遇到这两…...

【python】【sql】格式化注意事项
如果需要格式化表名到 sql 语句,sql 引擎是不支持的。 所以表名需要用字符串格式化,但其他参数最好用 sql 自带的格式,这样就不用去调一些细节,比如字符串的值是否要带引号之类的。 比如: cur.execute(SELECT {0} FR…...

leetcode做题笔记71
给你一个字符串 path ,表示指向某一文件或目录的 Unix 风格 绝对路径 (以 / 开头),请你将其转化为更加简洁的规范路径。 在 Unix 风格的文件系统中,一个点(.)表示当前目录本身;此外…...

啥是 Python?学了他能干嘛?
最近在学 python,真心感觉这玩意太牛了,你能想到,想不到的事情他都能做,前两天也是总结了一下 python 的特点,分享给大家看看~ 与君共勉 历史篇 1989年圣诞节,当大家都在忙着包装礼物,享受节日…...

百日筑基篇——Pandas学习三(pyhton入门八)
百日筑基篇——Pandas学习三(pyhton入门八) 文章目录 前言一、数据排序二、字符串处理三、数据合并方法1. merge方法2. concat方法 四、分组数据统计五、数据重塑1. stack2. pivot 总结 前言 上一篇文章介绍了一下pandas库中的一些函数,而本…...

【Android Framework系列】第10章 PMS之Hook实现广播的调用
1 前言 前面章节我们学习了【Android Framework系列】第4章 PMS原理我们了解了PMS原理,【Android Framework系列】第9章 AMS之Hook实现登录页跳转我们知道AMS可以Hook拦截下来实现未注册Activity页面的跳转,本章节我们来尝试一下HookPMS实现广播的发送。…...

Mysql锁实战
mysql版本:8.0.32 通过实战验证mysql的Record lock 与 Gap lock原理 准备工作 设置隔离级别为:RR,以及innodb状态输出锁相关信息 show variables like %innodb_status_output_locks%; show variables like %isolation%;set global innodb_…...
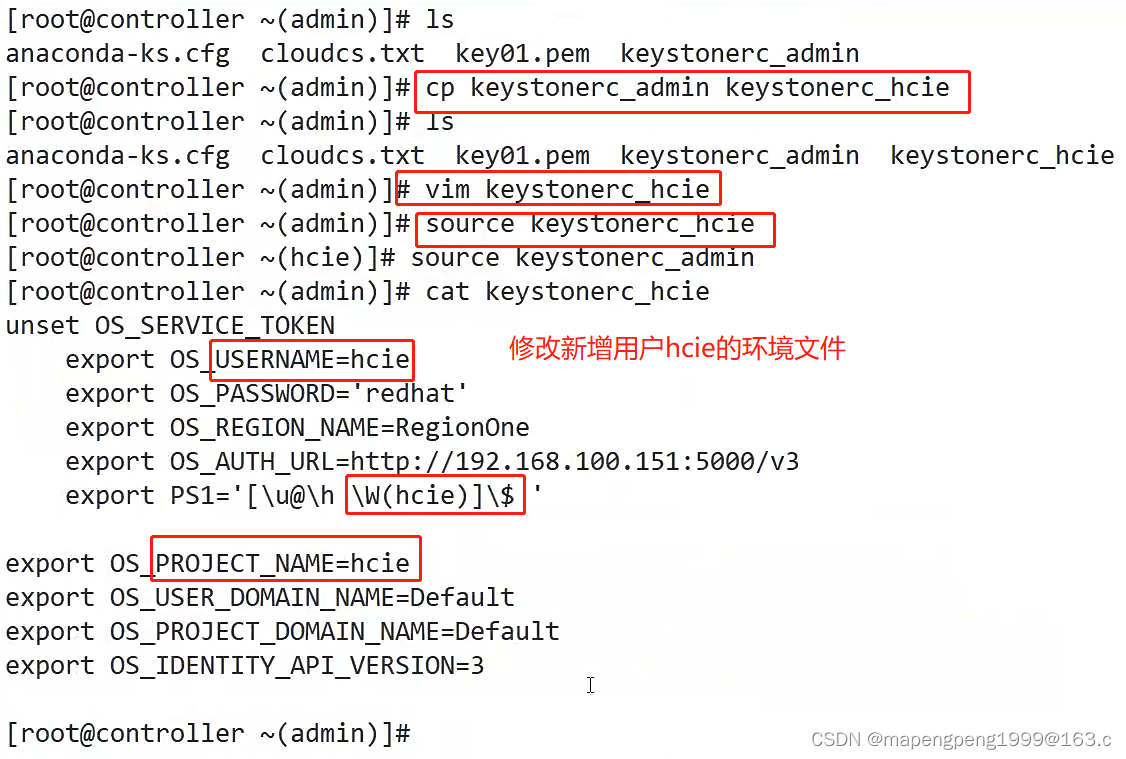
HCIP-OpenStack发放云主机
1、云中的概念 在云平台注册了一个账号,这个账号对于云平台来说,就是一个租户或者一个项目。 租户/项目(tenant/project),租户就是项目的意思。主机聚合就是主机组的意思。 region(区域)&…...

时序预测 | MATLAB基于扩散因子搜索的GRNN广义回归神经网络时间序列预测(多指标,多图)
时序预测 | MATLAB基于扩散因子搜索的GRNN广义回归神经网络时间序列预测(多指标,多图) 目录 时序预测 | MATLAB基于扩散因子搜索的GRNN广义回归神经网络时间序列预测(多指标,多图)效果一览基本介绍程序设计学习小结参考资料效果一览...
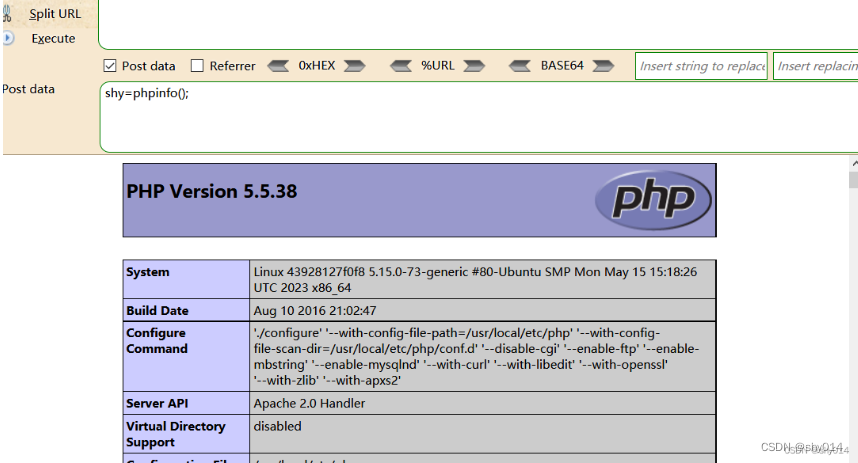
Vulhub之Apache HTTPD 换行解析漏洞(CVE-2017-15715)
Apache HTTPD是一款HTTP服务器,它可以通过mod_php来运行PHP网页。其2.4.0~2.4.29版本中存在一个解析漏洞,在解析PHP时,1.php\x0A将被按照PHP后缀进行解析,导致绕过一些服务器的安全策略。 1、docker-compose build、docker-compo…...
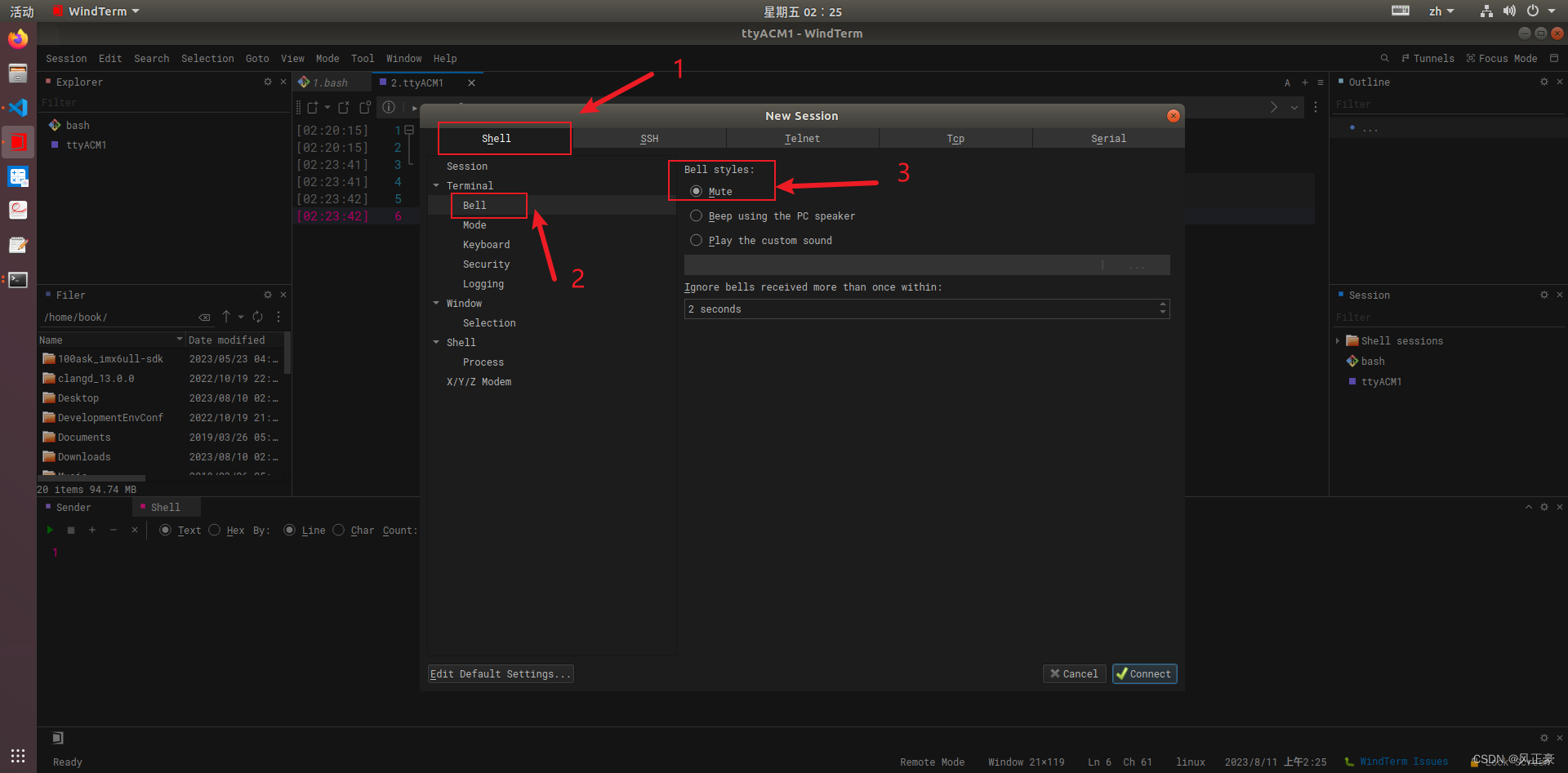
ARTS 挑战打卡的第7天 --- Ubuntu中的WindTerm如何设置成中文,并且关闭shell中Tab键声音(Tips)
前言 (1)Windterm是一个非常优秀的终端神器。关于他的下载我就不多说了,网上很多。今天我就分享一个国内目前没有找到的这方面的资料——Ubuntu中的WindTerm如何设置成中文,并且关闭shell中Tab键声音。 将WindTerm设置成中文 &…...

Oracle之执行计划
1、查看执行计划 EXPLAIN PLAN FOR SELECT * FROM temp_1 a ; SELECT * FROM TABLE(DBMS_XPLAN.DISPLAY); 2、执行计划说明 2.1、执行顺序 根据缩进来判断,缩进最多的最先执行;(缩进相同时,最上面的最先执行) 2.2…...

【Vue框架】菜单栏权限的使用与显示
前言 在 【Vue框架】Vue路由配置 中的getters.js里,可以看到有一个应用程序的状态(变量)叫 permission_routes,这个就是管理前端菜单栏的状态。具体代码的介绍,都以注释的形式来说明。 1、modules\permission.js 1…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

实战三:开发网页端界面完成黑白视频转为彩色视频
一、需求描述 设计一个简单的视频上色应用,用户可以通过网页界面上传黑白视频,系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观,不需要了解技术细节。 效果图 二、实现思路 总体思路: 用户通过Gradio界面上…...

如何配置一个sql server使得其它用户可以通过excel odbc获取数据
要让其他用户通过 Excel 使用 ODBC 连接到 SQL Server 获取数据,你需要完成以下配置步骤: ✅ 一、在 SQL Server 端配置(服务器设置) 1. 启用 TCP/IP 协议 打开 “SQL Server 配置管理器”。导航到:SQL Server 网络配…...

QT开发技术【ffmpeg + QAudioOutput】音乐播放器
一、 介绍 使用ffmpeg 4.2.2 在数字化浪潮席卷全球的当下,音视频内容犹如璀璨繁星,点亮了人们的生活与工作。从短视频平台上令人捧腹的搞笑视频,到在线课堂中知识渊博的专家授课,再到影视平台上扣人心弦的高清大片,音…...

python打卡第47天
昨天代码中注意力热图的部分顺移至今天 知识点回顾: 热力图 作业:对比不同卷积层热图可视化的结果 def visualize_attention_map(model, test_loader, device, class_names, num_samples3):"""可视化模型的注意力热力图,展示模…...

算法250609 高精度
加法 #include<stdio.h> #include<iostream> #include<string.h> #include<math.h> #include<algorithm> using namespace std; char input1[205]; char input2[205]; int main(){while(scanf("%s%s",input1,input2)!EOF){int a[205]…...
