算法随笔:图论问题之割点割边
割点
定义
割点的定义:如果一个点被删除之后会导致整个图不再是一个连通图,那么这个顶点就是这个图的割点。举例:
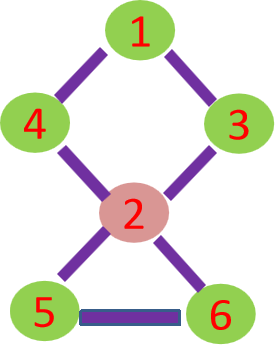
上图中的点2就是一个割点,如果它被删除,则整个图被分为两个连通分量,不再是一个连通图。
求割点的方法
最直观容易想到的一种简单朴素的方法:
依次删除每一个顶点,然后用dfs或者bfs来检查图是否依然连通。如果删除某个顶点后,导致图不再连通,那么刚才删除的顶点就是割点。
这种方法的时间复杂度是O(N(N+M))。显然不是一个高性能的算法。
考虑更高性能的算法:
考虑从根节点开始进行DFS遍历,遍历的同时记录每个节点的遍历顺序(又称为时间戳)到数组num。如下图:
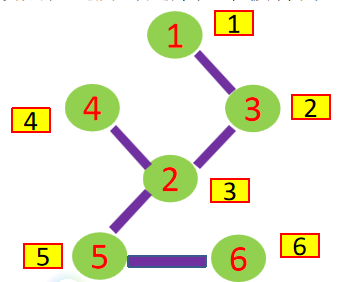
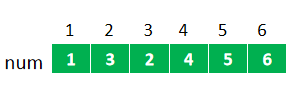
圆圈中数字是顶点编号, 圆圈右上角的数表示这个顶点的“时间戳” 。
那么在遍历过程中如何判断割点?见下表:
| 节点类型 | 判断方法 | 解释 |
|---|---|---|
| 根节点 | 对于根节点,有两棵及以上不相连的子树,则根节点是割点 | 很显然如果根节点有两棵及以上的不相连的子树,那么根节点被删除之后整个图将会不再是一个连通图,会被划分为多个连通块。 |
| 非根节点 | 对于非根节点,u的直接子v或者v的后代没有回退到u的祖先的边(没有不经过u直接回到u的祖先的路径),则u不是割点,否则是。 | 如果非根节点u的子节点v及v的后代节点有路径可以不经过点u回退到u的祖先,那么这个点即使被删除,整个图依然是连通的。 |
那么该算法具体如何实现呢?
定义一个数组low来记录每个顶点在不经过父顶点时,能够回到的最小“时间戳”。
对于某个顶点u,如果存在至少一个顶点v(u的儿子),使得low[v]>=num[u],即不能退回到祖先,顶多退回到顶点u,那么u点为割点。
示例代码(POJ1144)
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
using namespace std;
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
const int maxn = 1e2 + 10;
const int INF = 0x3fffffff;
const int mod = 1000000007;
int num[maxn]; // 记录每个点的dfs遍历顺序
int low[maxn]; // low[v]记录v和v的后代能连回到的祖先的num
int dfn; // 记录进入递归的顺序(也称为时间戳)
bool isCut[maxn]; // 标记割点
vector<int> G[maxn];void dfs(int u, int fa) { // 当前节点u,u的父节点falow[u] = num[u] = ++dfn; // 记录该点的遍历顺序,该点的low值初始等于numint child = 0; // 子树数目for (int i = 0; i < G[u].size(); i++) { // 处理u的所有子节点int v = G[u][i];if (!num[v]) { // v没访问过child++;dfs(v, u);low[u] = min(low[u], low[v]); // 用后代的返回值更新low值,从v以及v的后代可以回退到的祖先的num值if (low[v] >= num[u] && u != 1) { // 对于非根节点,u的直接子v或者v的后代没有回退到u的祖先的边,则u是割点isCut[u] = true;}} else if (num[v] < num[u] && v != fa) { // 处理回退边low[u] = min(low[u], num[v]);}}if (u == 1 && child >= 2) { // 对于根节点,有两棵以上不相连的子树,则根节点是割点isCut[1] = true;}
}void solve() {int n, ans;while (cin >> n, n) {if (n == 0)break;memset(low, 0, sizeof low);memset(num, 0, sizeof num);dfn = 0;for (int i = 1; i <= n; i++) {G[i].clear();}int a, b;while (cin >> a, a) {while (cin.get() != '\n') {cin >> b;G[a].push_back(b);G[b].push_back(a);}}memset(isCut, 0, sizeof isCut);ans = 0;dfs(1, 1);for (int i = 1; i <= n; i++) {ans += isCut[i];}cout << ans << endl;}
}int main() {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cout << fixed;cout.precision(18);solve();return 0;
}割边
定义
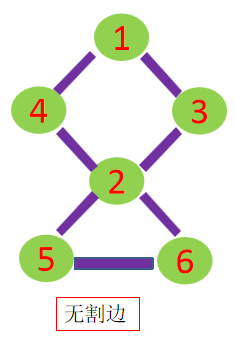
如果在一个无向图中删除某条边后,图不再连通,那么这条边叫做割边(又称桥)。举例:
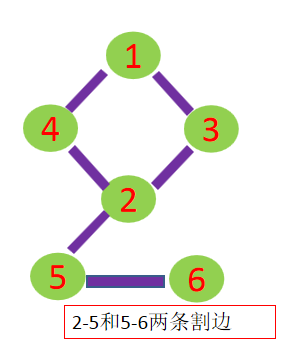
求割边的方法
只需将求割点的算法修改一个符号就可以。 只需将low[v]>=num[u]改为low[v]>num[u]。
这是为什么呢?
low[v]和num[u]相等则表示还可以回到父亲结点; 而low[v]>num[u]则表示连父亲都回不到了。倘若顶点v不能回到祖先,也没有另外的路能回到父亲,那么 u-v 这条边就是割边。
割边代码
……后边补上……
注:本文的部分内容和图片参考了 https://www.cnblogs.com/ljy-endl/p/11595161.html
相关文章:

算法随笔:图论问题之割点割边
割点 定义 割点的定义:如果一个点被删除之后会导致整个图不再是一个连通图,那么这个顶点就是这个图的割点。举例: 上图中的点2就是一个割点,如果它被删除,则整个图被分为两个连通分量,不再是一个连通图。…...
【虚幻引擎】UE5数字人的创建
安装插件 在插件里面找到MetaHuman,设置激活,然后重启引擎 找到bridge,并开启,这个需要我们制作完成的metahuman需要在这个插件里下载,unreal5自动安装 创建metahuman 首先添加一个metahuman本体,如果你的插…...

算法:深度优先遍历
文章目录 什么是深搜典型题目积累 本篇主要积累的是深度优先遍历算法 什么是深搜 深度优先搜索英文缩写为 DFS 即Depth First Search 其过程是对每一个可能的分支路径深入到不能再深入为止,而且每个节点只能访问一次 简单来说就是: 一路走到头,不撞墙…...
Stable Diffusion + Deform制作指南
1.安装sd以及deform插件,更新后记得重启 需要安装ffmpeg https://ffmpeg.org/download.html 选择对应版本然后安装 如果是windows需要解压后将ffmpeg的bin目录配置在电脑的环境变量里面。 2.准备一张初始开始图片 3.填写参数,这里面参数要注意,宽高一定是32的倍数。如果填写…...
ssm+vue网上花店设计源码和论文
ssmvue网上花店设计源码和论文017 开发工具:idea 数据库mysql5.7 数据库链接工具:navcat,小海豚等 技术:ssm 摘 要 网络技术和计算机技术发展至今,已经拥有了深厚的理论基础,并在现实中进行了充分运用…...

【leetcode】第一章数组
704. 二分查找 边界值需注意left代表左边界下标值,right代表右边界的下标值当数组只有一个元素时,此时如果找到该元素应该返回下标0,因此条件为left<right当mid的元素值大于target时,此时说明我们想找的target在右边ÿ…...

01|Java中常见错误或不清楚
补充:length vs length() vs size() 1 java中的length属性是针对数组说的,比如说你声明了一个数组,想知道这个数组的长度则用到了length这个属性. 2 java中的length()方法是针对字符串String说的,如果想看这个字符串的长度则用到length()这个方法. 3.java中的siz…...

递归的用法和例子
b站视频:https://www.bilibili.com/video/BV1iS4y1e7MJ/?spm_id_from333.999.0.0&vd_source1717654b9cbbc6a773c2092070686a95 # 递归的定义:其实就是自己调用自己,一般用函数的形式来进行 """ 特点: 1、一定…...

极狐GitLab 企业级 CI/CD 规模化落地实践指南(一)
目录 template 引用,减少代码冗余,增强 CI/CD 构建扩展性 问题 1:代码冗余,低效实践 问题 2:维护性难,工作量大 ➤ local ➤ file ➤ remote ➤ template 收益 1:一处修改,多…...
springBoot 简单的demo
springBoot 学习开始 场景开发流程1、创建项目2、导入依赖3、创建启动springBoot 项目的主入口程序4、创建业务程序5、在MainApplication文件运行程序6、将文件打包成jar包 遇到的问题未解决 希望大哥们帮忙--本地运行jar包报错 场景 浏览器发送hello请求,返回“he…...
)
[国产MCU]-BL602开发实例-实时时钟(RTC)
RTC 文章目录 RTC1、RTC介绍2、RTC使用实例RTC(real-time clock)为操作系统中的实时时钟设备,为操作系统提供精准的实时时间和定时报警功能。当设备下电后,通过外置电池供电,RTC继续记录操作系统时间;设备上电后,RTC提供实时时钟给操作系统,确保断电后系统时间的连续性。…...

大数据Flink(六十三):SqlClient工具的使用
文章目录 SqlClient工具的使用 一、入门...

哈威比例多路阀控制放大器
多路比例阀放大器控制负载敏感原理的比例多路换向阀,它用于与负载无关的、无级调节液压执行元件的运动速度。 多个执行元件可以同时和相互无关地进行工作。 这种类型的阀主要用于行走液压机械(例如:起重控制系统)。 通过选择执行元…...

Java bean 是个什么概念?
Java bean可以把它比作一个"智能的容器",它具备封装数据的能力。 Java bean是一种可重用的软件组件,它主要用于在Java应用程序中存储和传递数据。它是一种符合特定规范的Java类,通过封装数据和提供访问方法,使数据的管…...

微服务系列文章之 Springboot+Vue实现登录注册
一、springBoot 创建springBoot项目 分为三个包,分别为controller,service, dao以及resource目录下的xml文件。 UserController.java 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 …...

【Docker】如何在设计 dockerfile 过程中,设置容器启动后的定时任务
如何在设计 dockerfile 过程中,设置容器启动后的定时任务 jwensh 2023.08.14 文章目录 如何在设计 dockerfile 过程中,设置容器启动后的定时任务1. 基于 alpine 设计 dockerfile 过程中,设置容器启动后的定时任务2. 基于 CentOS 设计 Dockerf…...

【leetcode】第三章 哈希表part01
242.有效的字母异位词 使用HashMap public boolean isAnagram(String s, String t) {HashMap<Character,Integer> map new HashMap();int sLen s.length();int tLen t.length();if (sLen ! tLen) return false;// 统计词频for (int i 0; i < s.length(); i) {ch…...
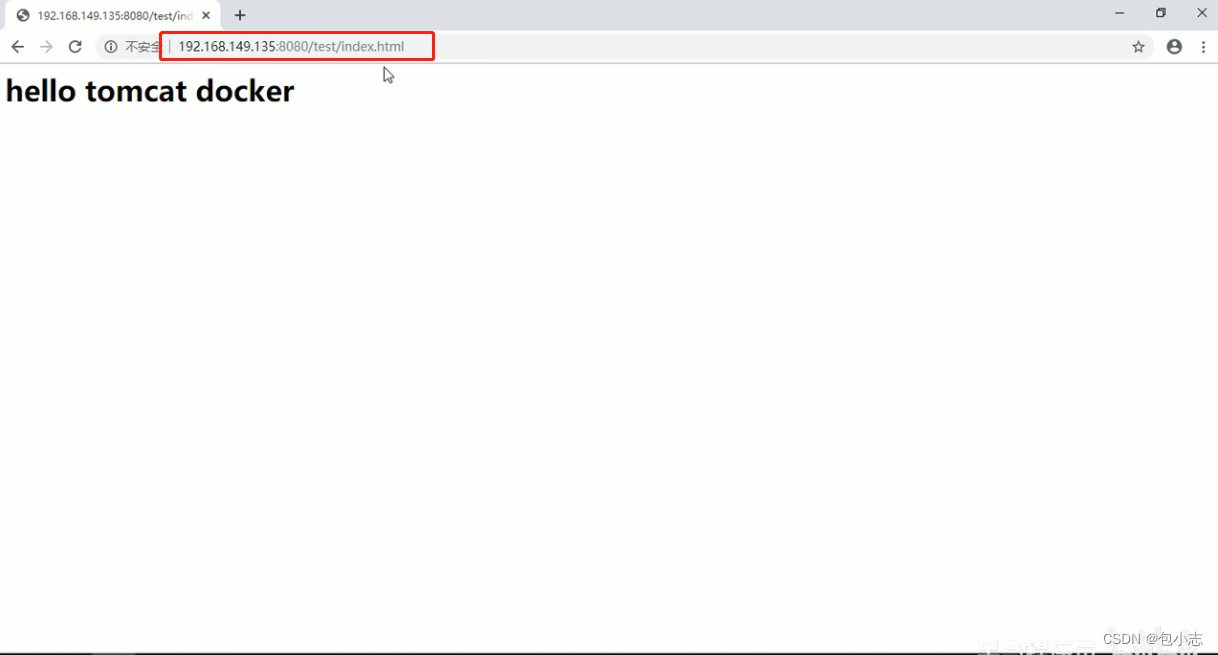
Docker中Tomcat部署步骤
第一次访问没有东西。...

pycharm 安装库
这是另一种方式。 搜索到的安装库的方式多数是:在桌面上winR键运行终端,输入命令,安装不了,发现安装不了。 1、打开pycharm; 2、软件下部的Terminal终端(需要运行一个代码才能出现,任何代码都可)…...
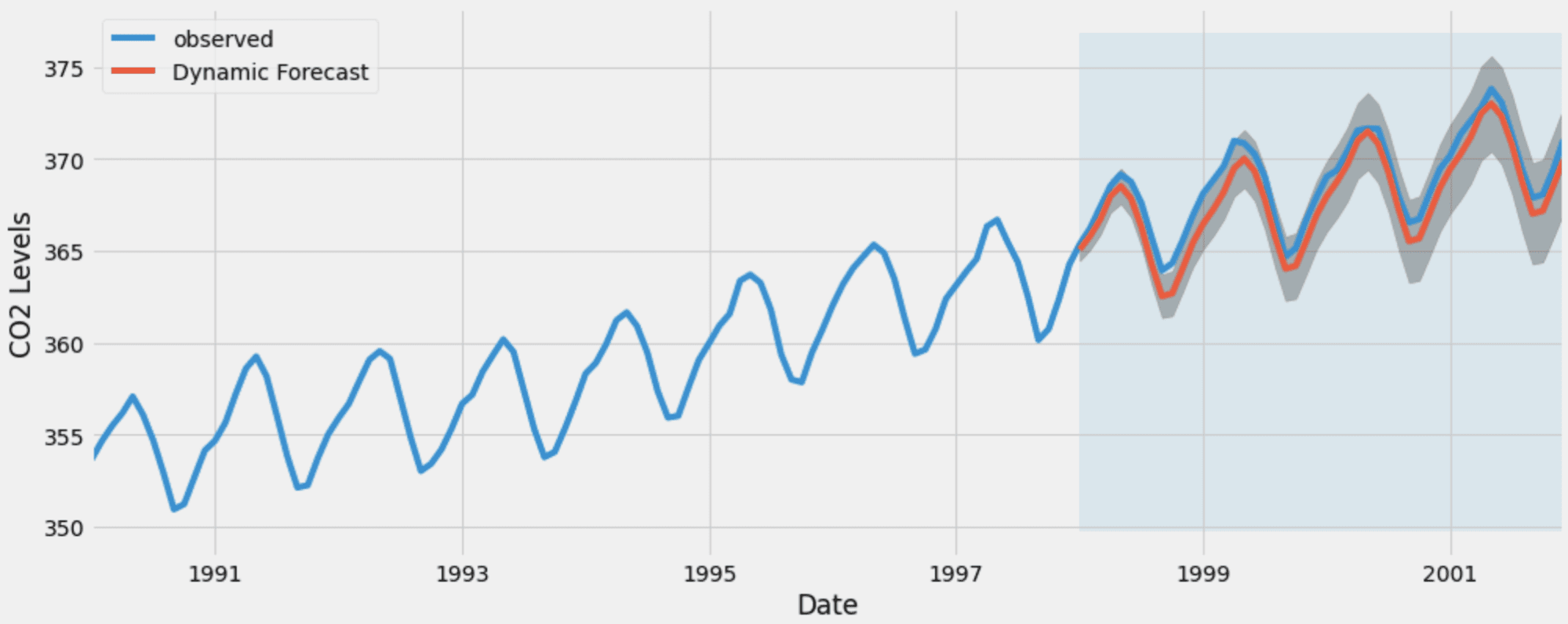
使用 Ploomber、Arima、Python 和 Slurm 进行时间序列预测
推荐:使用 NSDT场景编辑器助你快速搭建可二次编辑的3D应用场景 简短的笔记本说明 笔记本由 8 个任务组成,如下图所示。它包括建模的大多数基本步骤 - 获取数据清理、拟合、超参数调优、验证和可视化。作为捷径,我拿起笔记本并使用Soorgeon工具…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...

ZYNQ学习记录FPGA(一)ZYNQ简介
一、知识准备 1.一些术语,缩写和概念: 1)ZYNQ全称:ZYNQ7000 All Pgrammable SoC 2)SoC:system on chips(片上系统),对比集成电路的SoB(system on board) 3)ARM:处理器…...

前端高频面试题2:浏览器/计算机网络
本专栏相关链接 前端高频面试题1:HTML/CSS 前端高频面试题2:浏览器/计算机网络 前端高频面试题3:JavaScript 1.什么是强缓存、协商缓存? 强缓存: 当浏览器请求资源时,首先检查本地缓存是否命中。如果命…...
与文本切分器(Splitter)详解《二》)
LangChain 中的文档加载器(Loader)与文本切分器(Splitter)详解《二》
🧠 LangChain 中 TextSplitter 的使用详解:从基础到进阶(附代码) 一、前言 在处理大规模文本数据时,特别是在构建知识库或进行大模型训练与推理时,文本切分(Text Splitting) 是一个…...
