数据结构:堆的实现
1.堆的概念
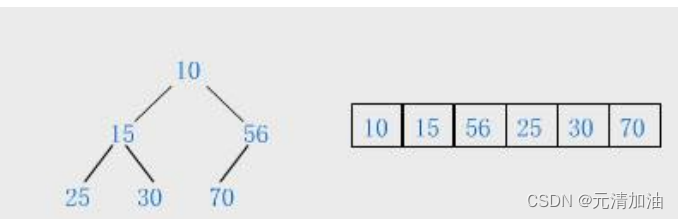
如果有一个关键码的集合 K = { k1 ,k2 ,k3 ,…,kn },把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中,并且 k(i) < k(i*2+1) 和 k(i) < k(i*2+2), i = 0 , 1 , 2…,则称为小堆 ( 或大堆 ) 。将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。
1.1堆的性质
堆中某个节点的值总是不大于或不小于其父节点的值;堆总是一棵完全二叉树。
1.2堆的存储结构
2.堆的实现
堆的构建堆的销毁堆的插入堆的删除取堆顶的数据堆的数据个数堆的判空
2.1堆的构造与销毁
void HeapInit(HP* php) {assert(php);php->a = NULL;php->size = 0;php->capacity = 0; }void HeapDestroy(HP* php) {assert(php);free(php->a);php->a = NULL;php->size = 0;php->capacity = 0; }
2.2堆的向上与向下调整
void swap(DataType*str1, DataType*str2) {DataType temp = *str1;*str1 = *str2;*str2 = temp; } //向上调整(前提是上面是一个堆) void AdjustUp(DataType* a, int child) {//利用孩子找父亲,并且比较int parent = (child - 1) / 2;while (child > 0){// "<" 和 ">"取决与建立大小堆if (a[child] < a[parent]){swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}} } //向下调整(前提是下面左右子树是一个堆) void AdjustDown(int* a, int n, int parent)//n是数量 {//利用父亲找儿子并比较大小int child = parent * 2 + 1;while (child < n){//child + 1 < n可能没有右孩子,防止越界风险if (child + 1 < n && a[child + 1] < a[child]){child++;}// "<" 和 ">"取决与建立大小堆if (a[child] > a[parent]){swap(&a[child], &a[parent]);parent = child;int child = parent * 2 + 1;}elsebreak;} }
2.3 堆的插入与堆的删除
//先插入一个数到数组的尾上,再进行向上调整算法,直到满足堆 void HeapPush(HP* php, DataType x) {assert(php);//判断是否要扩容if (php->size == php->capacity){int newCapacity = php->capacity == 0 ? 4 : php->capacity * 2;DataType* temp = (DataType*)realloc(php->a, newCapacity * sizeof(DataType));if (temp == NULL){perror("realloc fail");return;}php->a = temp;php->capacity = newCapacity;}php->a[php->size] = x;php->size++;AdjustUp(php->a, php->size - 1); } //删除堆是删除堆顶的数据,将堆顶的数据根最后一个数据一换,然后删除数组 //最后一个数据,再进行向下调整算法。 void HeapPop(HP* php) {assert(php);swap(&php->a[0], &php->a[php->size - 1]);php->size--;AdjustDown(php->a, php->size, 0); }
2.4堆的数据个数与堆的判空和取得堆的堆顶元素
DataType HeapTop(HP* php) {assert(php);assert(!HeapEmpty(php));return php->a[0]; } bool HeapEmpty(HP* php) {assert(php);return php->size == 0; }int HeapSize(HP* php) {assert(php);return php->size; }
相关文章:
数据结构:堆的实现
1.堆的概念 如果有一个关键码的集合 K { k1 ,k2 ,k3 ,…,kn },把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中,并且 k(i) < k(i*21) 和 k(i) < k(i*22), i 0 ÿ…...
zabbix-6.4 监控 MySQL
目录 1、rpm安装zabbix_agentd服务 2、编写zabbix_agentd.conf文件 3、编写模板文件 4、创建mysql用户并赋权限 5、创建.my.cnf文件 6、将规则添加到SELinux策略中 注意: 若模板无法读取.my.cnf 信息,从而导致监控报错,可以尝试修改模…...
深入探索:解读创意的力量——idea的下载、初步使用
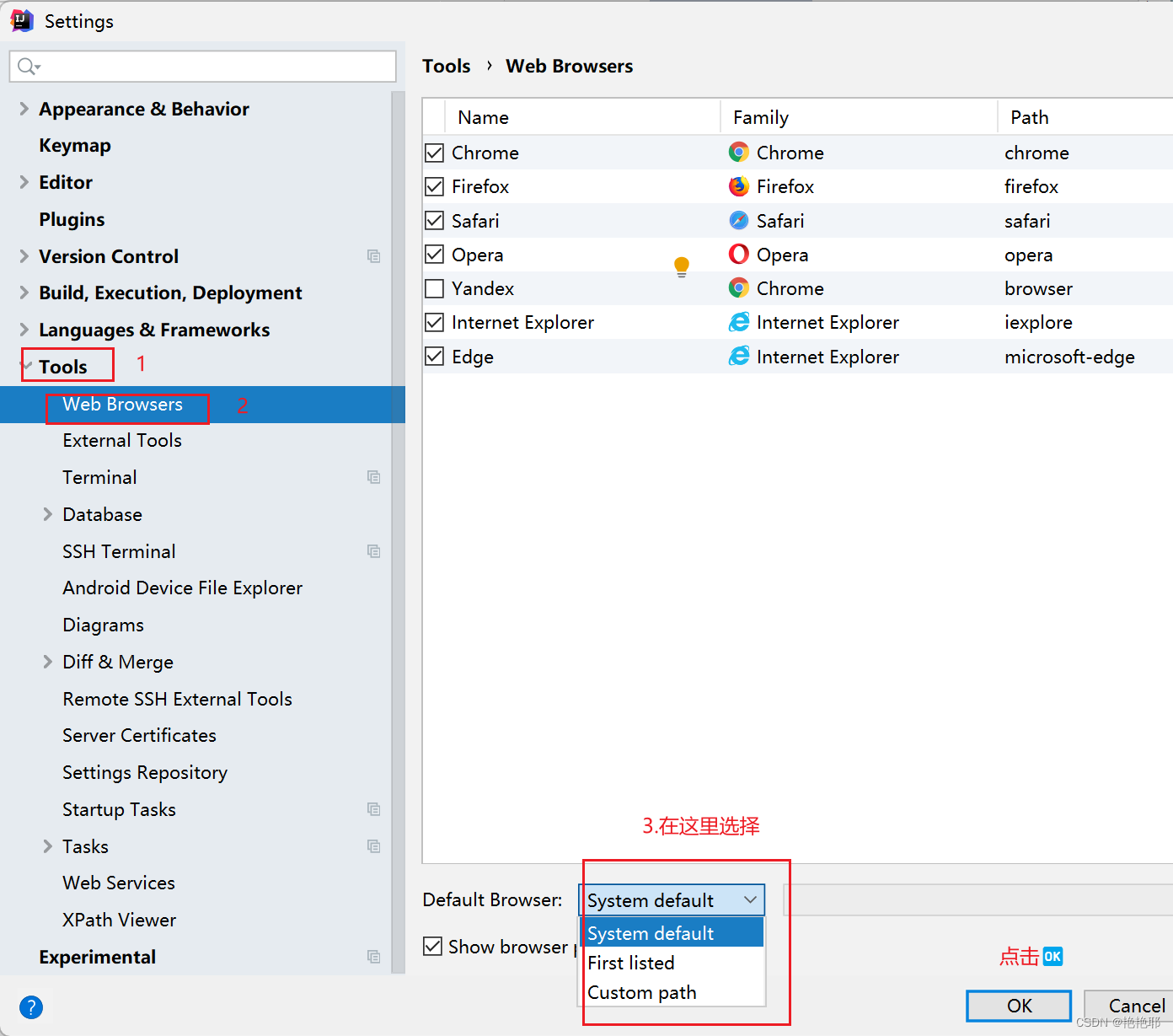
目录 编辑 1.IDEA的简介 2.IDEA的下载 2.1下载路径https://www.jetbrains.com/zh-cn/idea/download/?sectionwindows编辑 2.2下载的步骤 3 idea的初步使用 3.1新建一个简单的Java项目 3.1.1首先需要创建一个新的工程 3.1.2创建一个新的项目(模块&am…...

Redis详解
Redis 简介 Redis(Remote Dictionary Server)是一个开源的高性能键值对存储数据库,最初由 Salvatore Sanfilippo 开发,它在内存中存储数据,并提供了持久化功能,可以将数据保存到磁盘中,是一种N…...
【Linux】高级IO
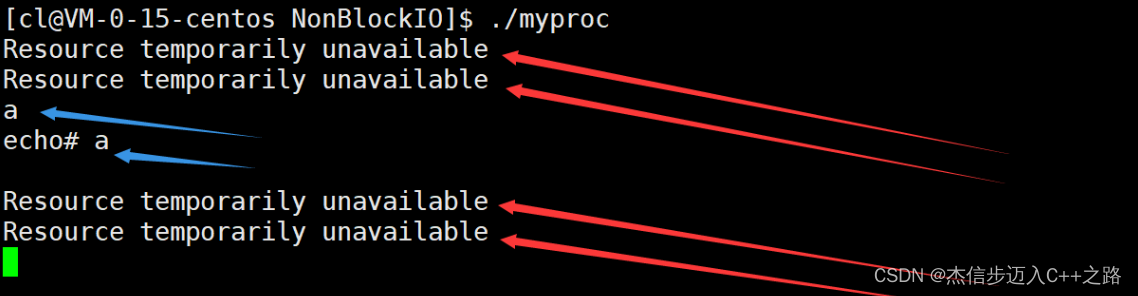
目录 IO的基本概念 钓鱼五人组 五种IO模型 高级IO重要概念 同步通信 VS 异步通信 阻塞 VS 非阻塞 其他高级IO 阻塞IO 非阻塞IO IO的基本概念 什么是IO? I/O(input/output)也就是输入和输出,在著名的冯诺依曼体系结构当中…...

动态HTTP代理与竞争情报收集的关联
Hey,各位爬友们!作为一名专业的爬虫HTTP代理提供者,今天我要和大家聊一聊动态HTTP代理与竞争情报收集之间的关联。在这篇文章中,我将向大家解释怎么使用动态HTTP代理完成在竞争中的情报收集,并分享一些实用的技巧。 首…...
kafka基本概念及操作
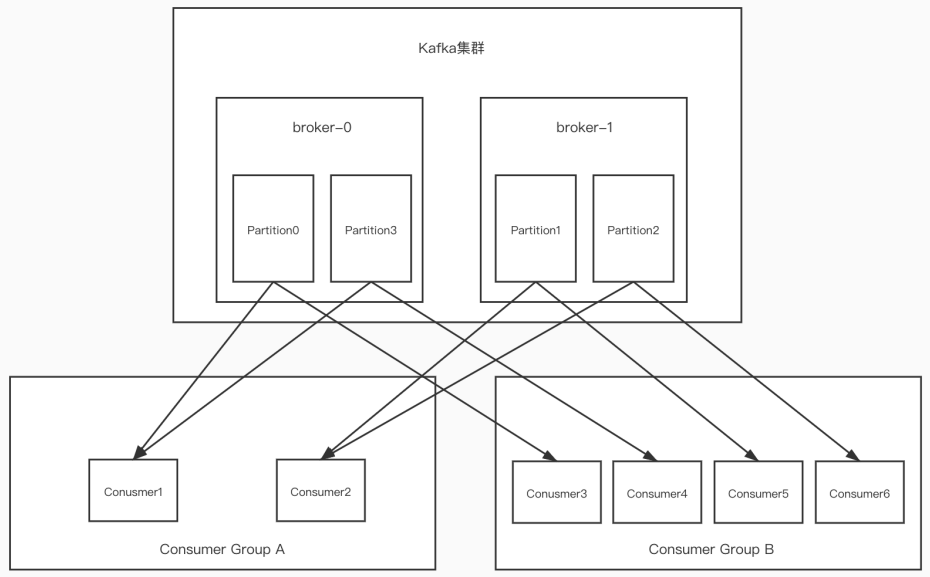
kafka介绍 Kafka是最初由Linkedin公司开发,是一个分布式、支持分区的(partition)、多副本的 (replica),基于zookeeper协调的分布式消息系统,它的最大的特性就是可以实时的处理大量数据以满足各…...

分享个试卷去笔迹什么软件,几个步骤轻松擦除
试卷擦去笔迹是一项非常关键的技能,它可以帮助你更好地管理你的笔记和文件。不管是小伙伴们想重新测试试卷或者是将试卷输出为电子版,都可以实现的。在这篇文章中,我将分享一些方法和软件,帮助你更好地进行试卷擦除。有需要的小伙…...

ClickHouse(十八):Clickhouse Integration系列表引擎
进入正文前,感谢宝子们订阅专题、点赞、评论、收藏!关注IT贫道,获取高质量博客内容! 🏡个人主页:含各种IT体系技术,IT贫道_Apache Doris,大数据OLAP体系技术栈,Kerberos安全认证-CSDN博客 &…...

日常BUG——代码提交到了本地但是没有push,删除了本地分支如何恢复
😜作 者:是江迪呀✒️本文关键词:日常BUG、BUG、问题分析☀️每日 一言 :存在错误说明你在进步! 一、问题描述 代码在本地提交了,但是没有push到远程,然后删除了本地的分支。想要恢…...
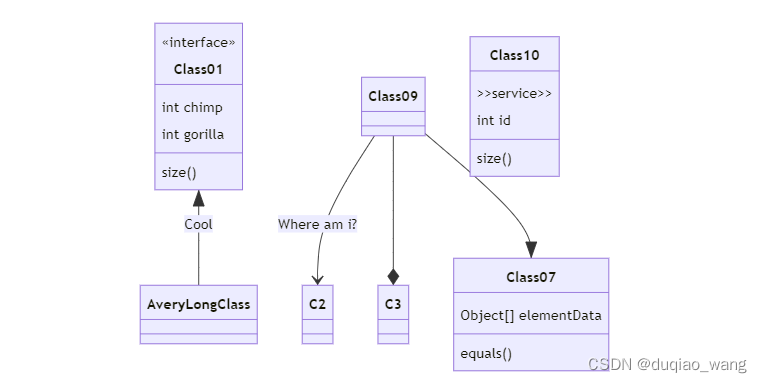
Markdown语法
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 Markdown语法目录 前言1.标题2.文本样式3.列表四.图片5.链接6.目录7.代码片7.表格8.注脚9.注释10.自定义列表11.LaTeX数学公式12.插入甘特图13.插入UML图14.插入Merimaid流程…...

vue3表格,编辑案例
index.vue <script setup> import { onMounted, ref } from "vue"; import Edit from "./components/Edit.vue"; import axios from "axios";// TODO: 列表渲染 const list ref([]); const getList async () > {const res await ax…...
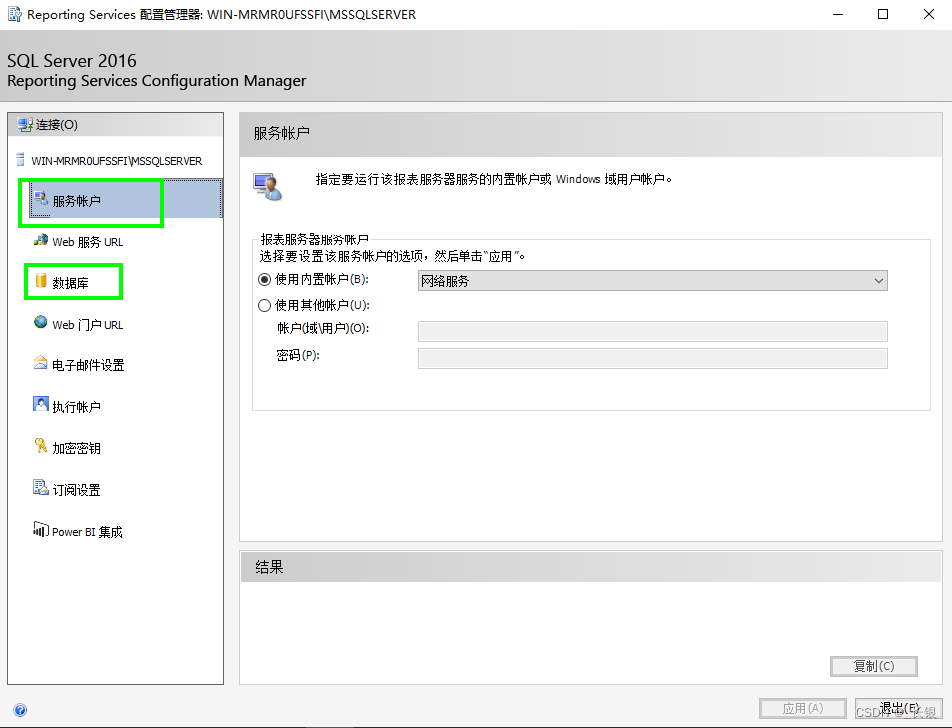
SQL Server Reporting Services 报错:报表服务器无法访问服务帐户的私钥
解决这个问题,有小伙伴提到可以使用命令 exec DeleteEncryptedContent 但这对这边的环境时行不通的,我在【服务账户】的配置和【数据库】的配置中到使用了域账户,试了几次都不行。改成使用内置账户就好了。具体原因还没扒拉(欢迎…...
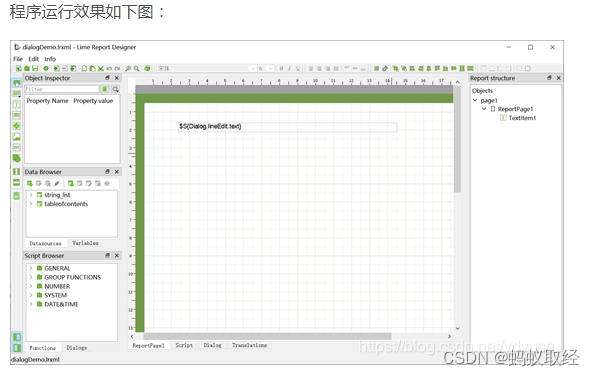
QT报表Limereport v1.5.35编译及使用
1、编译说明 下载后QT CREATER中打开limereport.pro然后直接编译就可以了。编译后结果如下图: 一次编译可以得到库文件和DEMO执行程序。 2、使用说明 拷贝如下图编译后的lib目录到自己的工程目录中。 release版本的重新命名为librelease. PRO文件中配置 QT …...

互联网发展历程:从中继器口不够到集线器的引入
互联网的发展,就像一场不断演进的技术盛宴,每一步的变革都在推动着我们的世界向前。然而,在网络的早期,一项重要的技术问题曾困扰着人们:当中继器的接口数量不足时,如何连接更多的设备?这时&…...

vue+flask基于知识图谱的抑郁症问答系统
vueflask基于知识图谱的抑郁症问答系统 抑郁症已经成为当今社会刻不容缓需要解决的问题,抑郁症的危害主要有以下几种:1.可导致病人情绪低落:抑郁症的病人长期处于悲观的状态中,感觉不到快乐,总是高兴不起来。2.可导致工…...

操作格子---算法集
问题描述 有 n 个格子,从左到右放成一排,编号为 1-n。 共有 m 次操作,有 3 种操作类型: 1.修改一个格子的权值。 2.求连续一段格子权值和。 3.求连续一段格子的最大值。 对于每个 2、3 操作输出你所求出的结果。 输入格式 第一行 …...

科研绘图chapter1:绘图原则与配色基础
本系列会持续更新,主要参考datawhale的开源课程。详见: https://github.com/datawhalechina/paper-chart-tutorial 文章目录 1.1 科研论文配图的绘制基础1.2 科研论文配图的配色基础1.2.1 配色模式1.2.2 色环配色原则1.3 配色工具/网站 1.1 科研论文配图…...

Linux下grep通配容易混淆的地方
先上一张图: 我希望找到某个版本为8的一个libXXX.8XXX.so ,那么应该怎么写呢? 先看这种写法对不对: 是不是结果出乎你的意料之外? 那么我们来看一下规则: 这里的 "*" 表示匹配前一个字符的零个或多个 于是我们就不难理解了: lib*8*.so 表示 包…...

WebRTC音视频通话-WebRTC本地视频通话使用ossrs服务搭建
iOS开发-ossrs服务WebRTC本地视频通话服务搭建 之前开发中使用到了ossrs,这里记录一下ossrs支持的WebRTC本地服务搭建。 一、ossrs是什么? ossrs是什么呢? SRS(Simple Realtime Server)是一个简单高效的实时视频服务器,支持RTM…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...
