【Leetcode Sheet】Weekly Practice 2
Leetcode Test
1281 整数的各位积和之差(8.9)
给你一个整数 n,请你帮忙计算并返回该整数「各位数字之积」与「各位数字之和」的差。
提示:
1 <= n <= 10^5
【原始代码】:
int subtractProductAndSum(int n){//1 <= n <= 10^5//except 100000, there're 5 bitsif(n==100000){return -1;}int bits[5]={0,0,0,0,0,0};int cnt=0;while(n>0){bits[cnt++]=n%10;n/=10;}int multi=1,sum=0;for(int i=0;i<cnt;i++){multi*=bits[i];sum+=bits[i];}return (multi-sum);
}
【优化代码】
int subtractProductAndSum(int n) {int m = 1, s = 0; //m是乘积,sum是求和while (n) { //当n!=0时int x = n % 10; //x是n的余数n /= 10; //n缩小m *= x; //m进行乘积s += x; //s进行求和}return m - s; //返回 乘积-求和
}
//减少位数的存储,空间复杂度为O(1)
//时间复杂度仍然为O(m),m为n的位数
【其他思路】
将n转为字符串,例如n是1234,则char temp=‘1234’
后续直接遍历strlen(temp),计算temp[i]-'0’的值即可
1289 下降路径最小和 II(8.10)
给你一个 n x n 整数矩阵 grid ,请你返回 非零偏移下降路径 数字和的最小值。
非零偏移下降路径 定义为:从 grid 数组中的每一行选择一个数字,且按顺序选出来的数字中,相邻数字不在原数组的同一列。
提示:
n == grid.length == grid[i].length1 <= n <= 200-99 <= grid[i][j] <= 99
int minFallingPathSum(int** grid, int gridSize, int* gridColSize) {int first_min_sum = 0;int second_min_sum = 0;int first_min_index = -1;for (int i = 0; i < gridSize; i++) { //遍历外层int cur_first_min_sum = INT_MAX; //记录最小值int cur_second_min_sum = INT_MAX; //记录次小值int cur_first_min_index = -1; //记录最小值列编号for (int j = 0; j < gridSize; j++) { //遍历内层int cur_sum = (j != first_min_index ? first_min_sum : second_min_sum) + grid[i][j];//当前求和计算,如果j和最小值列编号不一样,则添加最小值,否则添加次小值if (cur_sum < cur_first_min_sum) { //如果当前求和,小于最小cur_second_min_sum = cur_first_min_sum; //更新次小为之前的最小cur_first_min_sum = cur_sum; //更新最小为当前的求和cur_first_min_index = j; //更新比列编号} else if (cur_sum < cur_second_min_sum) { //如果当前求和,小于次小cur_second_min_sum = cur_sum; //更新次小为当前的求和}}first_min_sum = cur_first_min_sum; //更新最小second_min_sum = cur_second_min_sum; //更新次小first_min_index = cur_first_min_index; ///更新列编号}return first_min_sum;
}
1572 矩阵对角线元素的和(8.11)
给你一个正方形矩阵 mat,请你返回矩阵对角线元素的和。
请你返回在矩阵主对角线上的元素和副对角线上且不在主对角线上元素的和。
提示:
n == mat.length == mat[i].length1 <= n <= 1001 <= mat[i][j] <= 100
int diagonalSum(int** mat, int matSize, int* matColSize){//n x n matrixint n=matSize,sum=0;for(int i=0;i<n;i++){for(int j=0;j<n;j++){if((i==j)||(i+j==n-1)){ //i==j 主对角线;i+j==n-1 次对角线sum+=mat[i][j];}}}return sum;
}
2681 英雄的力量(8.1补)
给你一个下标从 0 开始的整数数组 nums ,它表示英雄的能力值。如果我们选出一部分英雄,这组英雄的 力量 定义为:
i0,i1,…ik表示这组英雄在数组中的下标。那么这组英雄的力量为max(nums[i0],nums[i1] ... nums[ik])2 * min(nums[i0],nums[i1] ... nums[ik])。
请你返回所有可能的 非空 英雄组的 力量 之和。由于答案可能非常大,请你将结果对 109 + 7 取余。
提示:
1 <= nums.length <= 1051 <= nums[i] <= 109
int cmp(void *a,void *b){return *(int*)a-*(int*)b;
}int sumOfPower(int* nums, int numsSize){qsort(nums,numsSize,sizeof(int),cmp); //元素的顺序不影响答案,先排序//power = max*max*minint dp = 0, preSum = 0;int res = 0, mod = 1e9 + 7;for (int i = 0; i < numsSize; i++) {dp = (nums[i] + preSum) % mod;preSum = (preSum + dp) % mod;res = (int) ((res + (long long) nums[i] * nums[i] % mod * dp) % mod);if (res < 0) {res += mod;}}return res;
}
23 合并K个升序链表(8.12)
给你一个链表数组,每个链表都已经按升序排列。
请你将所有链表合并到一个升序链表中,返回合并后的链表。
提示:
k == lists.length0 <= k <= 10^40 <= lists[i].length <= 500-10^4 <= lists[i][j] <= 10^4lists[i]按 升序 排列lists[i].length的总和不超过10^4
/*** Definition for singly-linked list.* struct ListNode {* int val;* struct ListNode *next;* };*/int cmp(const void * a, const void * b)//升序子函数
{return *(int *)a - *(int *)b;
}
struct ListNode* mergeKLists(struct ListNode** lists, int listsSize){if(listsSize == 0 ){return NULL;}int ans[10000];//临时保存链表值int node = 0;for(int i = 0; i <listsSize; i++)//保存所有链表值{while(lists[i]){ans[node++] = lists[i]->val;lists[i] = lists[i]->next;}}qsort(ans, node, sizeof(int), cmp);//排序struct ListNode * h = NULL;struct ListNode * root = NULL;for(int i = 0; i < node; i++)//转换为链表存储{struct ListNode * r = malloc(sizeof(struct ListNode));r->val = ans[i];r->next = NULL;if(root == NULL){h = r;root = r;}else{h->next = r;h = r;} }return root;
}
88 合并两个有序数组(8.13)
给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。
请你 合并 nums2 到 nums1 中,使合并后的数组同样按 非递减顺序 排列。
**注意:**最终,合并后数组不应由函数返回,而是存储在数组 nums1 中。为了应对这种情况,nums1 的初始长度为 m + n,其中前 m 个元素表示应合并的元素,后 n 个元素为 0 ,应忽略。nums2 的长度为 n 。
提示:
nums1.length == m + nnums2.length == n0 <= m, n <= 2001 <= m + n <= 200-109 <= nums1[i], nums2[j] <= 109
int cmp(void *a,void *b){return *(int*)a-*(int*)b;
}void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n){int cnt=0,i=m;while(cnt<n){nums1[i++]=nums2[cnt++];}qsort(nums1,(n+m),sizeof(int),cmp);
}
a former method
void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n){for(int i=0;i!=n;i++){nums1[m+i]=nums2[i];}int minno;for(int i=0;i<m+n-1;i++){minno=i;for(int j=i+1;j<m+n;j++){if(nums1[j]<nums1[minno]){minno=j;}}//找到i后面的最小数,交换i位置和minno位置int temp=nums1[i];nums1[i]=nums1[minno];nums1[minno]=temp;}
}
a new-spaced method: O(n+m) of both time and space
void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n) {int p1 = 0, p2 = 0;int sorted[m + n]; //new-spacedint cur;while (p1 < m || p2 < n) {if (p1 == m) {cur = nums2[p2++];} else if (p2 == n) {cur = nums1[p1++];} else if (nums1[p1] < nums2[p2]) {cur = nums1[p1++];} else {cur = nums2[p2++];}sorted[p1 + p2 - 1] = cur;}for (int i = 0; i != m + n; ++i) {nums1[i] = sorted[i];}
}
617 合并二叉树(8.14)
给你两棵二叉树: root1 和 root2 。
想象一下,当你将其中一棵覆盖到另一棵之上时,两棵树上的一些节点将会重叠(而另一些不会)。你需要将这两棵树合并成一棵新二叉树。合并的规则是:如果两个节点重叠,那么将这两个节点的值相加作为合并后节点的新值;否则,不为 null 的节点将直接作为新二叉树的节点。
返回合并后的二叉树。
注意: 合并过程必须从两个树的根节点开始。
提示:
- 两棵树中的节点数目在范围
[0, 2000]内 -104 <= Node.val <= 104
/*** Definition for a binary tree node.* struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* };*///深度优先搜索 dfs
struct TreeNode* mergeTrees(struct TreeNode* root1, struct TreeNode* root2){//如果两个节点重叠,那么将这两个节点的值相加作为合并后节点的新值;//否则,不为 null 的节点将直接作为新二叉树的节点。if(root1 == NULL) return root2;else if(root2 == NULL) return root1;struct TreeNode* result=malloc(sizeof(struct TreeNode));result->val=root1->val + root2->val;result->left=mergeTrees(root1->left,root2->left); //左子树递归result->right=mergeTrees(root1->right,root2->right); //右子树递归return result;
}
C++:
递归,直接在原root1进行修改
class Solution {
public:TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {if (root1 && root2) {root1->val += root2->val;root1->left = mergeTrees(root1->left, root2->left);root1->right = mergeTrees(root1->right, root2->right);}return root1 ? root1 : root2;}
};
另可进行广度优先(较为复杂)
相关文章:

【Leetcode Sheet】Weekly Practice 2
Leetcode Test 1281 整数的各位积和之差(8.9) 给你一个整数 n,请你帮忙计算并返回该整数「各位数字之积」与「各位数字之和」的差。 提示: 1 < n < 10^5 【原始代码】: int subtractProductAndSum(int n){//1 < n < 10^5//…...
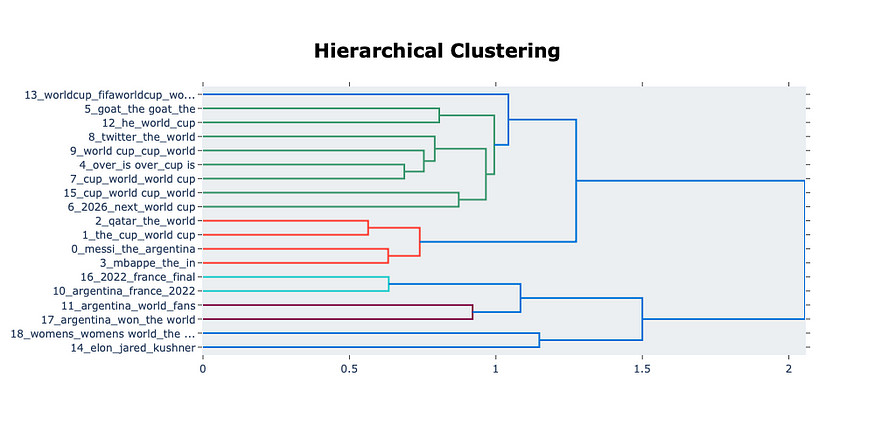
【BERTopic应用 03/3】:微调参数
一、说明 一般来说,BERTopic 在开箱即用的模型中工作得很好。但是,当您有数百万个数据要处理时,使用基本模型处理数据可能需要一些时间。在这篇文章中,我将向您展示如何微调BERTopic中的一些参数并比较它们的结果。让我们潜入。 二…...
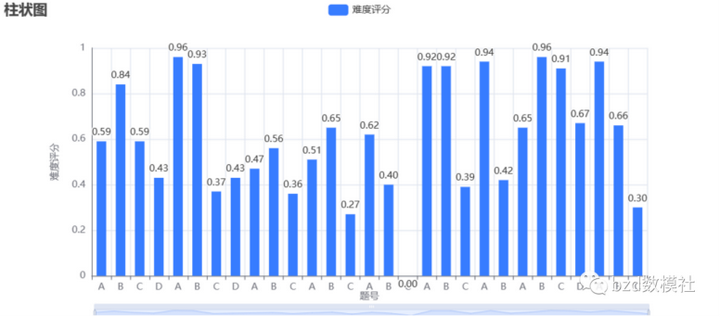
2023年上半年数学建模竞赛题目汇总与难度分析
2023年上半年数学建模竞赛题目汇总与难度分析 由于近年来国赛ABC题出题方式漂浮不定,没有太大的定性,目前总体的命题方向为,由之前的单一模型问题变为数据分析评价优化或者预测类题目是B、C题的主要命题方向。为了更好地把握今年命题的主方…...

Linux下搭建java环境
文章目录 一,xshell链接linux二,linux安装jdk环境 一,xshell链接linux 这里用到的工具,VMware搭配CentOS7 64位Xshell5 操作之前确保,传输Xshell连接了虚拟机 打开Xshell,文件->新建 主机ip—>进入虚拟机,右键打开终端,输入命令:ifco…...

String、StringBuffer、StringBuilder三者的异同?
String字符串 不可变的字符序列在 jdk1.8,我们底层用 char [ ] 存储在 jdk 17,我们底层用 byte [ ] 存储 StringBuffer字符串缓冲区类 可变的字符序列,线程安全的(synchronized),效率低在 jdk1.8…...

htmlCSS-----弹性布局案例展示
目录 前言 效果展示 编辑 代码 思路分析 前言 上一期我们学习了弹性布局,那么这一期我们用弹性布局来写一个小案例,下面看代码(上一期链接html&CSS-----弹性布局_灰勒塔德的博客-CSDN博客) 效果展示 代码 html代码&am…...

Fiddler模拟请求发送和修改响应数据
fiddler模拟伪造请求 方法一:打断点模拟HTTP请求 1、浏览器页面填好内容后(不要操作提交),打开fiddler,设置请求前断点,点击菜单fiddler,”Rules”\”Automatic Breakpoints”\”Before Requests” 2、在…...

RH850从0搭建Autosar开发环境【23】- Davinci Configurator之DCM实操实现DID的读取写入
配置DID 一、Developer中创建SWC1.1 创建Application Component Type1.2 实例化Component二、在SWC中创建接口以及Runnable2.1 创建DID的Service Ports2.2 创建DID的Service Runnable三、在Configurator连接接口以及生成代码3.1 连接DCM与SWC3.2 生成RTE3.3 生成SWC的DID的模板…...
ChatGPT收录
VSCode插件-ChatGPT 多磨助手 多磨助手 (domore.run) Steamship Steamship 免费合集 免费chatGPT - Ant Design Pro 免费AI聊天室 (xyys.one)...

Nginx随笔
Nginx下载链接 安装命令: apt update apt install nginx 一、基础命令(Ubuntu) 1、在全局 nginx -t //检查Nginx的配置文件是否有错 systemctl start nginx //启动Nginx systemctl stop nginx //停止Nginx systemctl status nginx //查…...
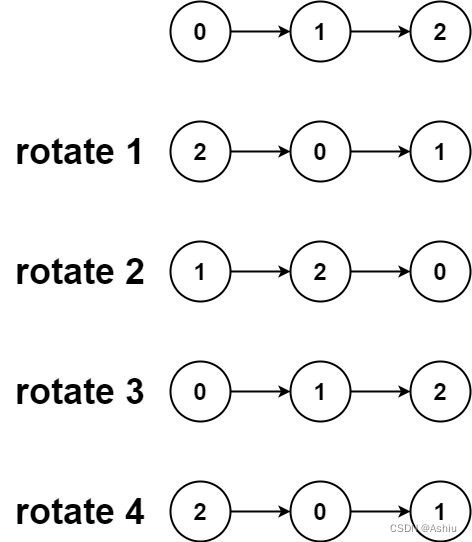
61. 旋转链表
61. 旋转链表 题目-中等难度示例1. 快慢指针找到分割位置2. 连成环后截断 题目-中等难度 相关企业 给你一个链表的头节点 head ,旋转链表,将链表每个节点向右移动 k 个位置。 示例 示例 1: 输入:head [1,2,3,4,5], k 2 输出…...

Python实现动态调用Matlab自定义函数
首先需要下载与python版本对应的matlab,并成功执行matlab中的setup.py文件 参考流程如下 https://blog.csdn.net/s1k9y9/article/details/127793053 完成上述步骤即可开始实现动态调用matlab文件。 文件目录如下 D://call/ |–matlab |–test1 |–main.m |–test2 |…...

redis集群和分片-Redis Cluster:分布式环境中的数据分片、主从复制和 Sentinel 哨兵
当涉及到 Redis 中的集群、分片、主从复制和 Sentinel 哨兵时,这些是构建分布式 Redis 环境中非常重要的概念和组件。下面详细介绍这些概念以及它们在分布式环境中的作用。 Redis Cluster Redis Cluster 是 Redis 官方提供的分布式解决方案,用于管理和…...
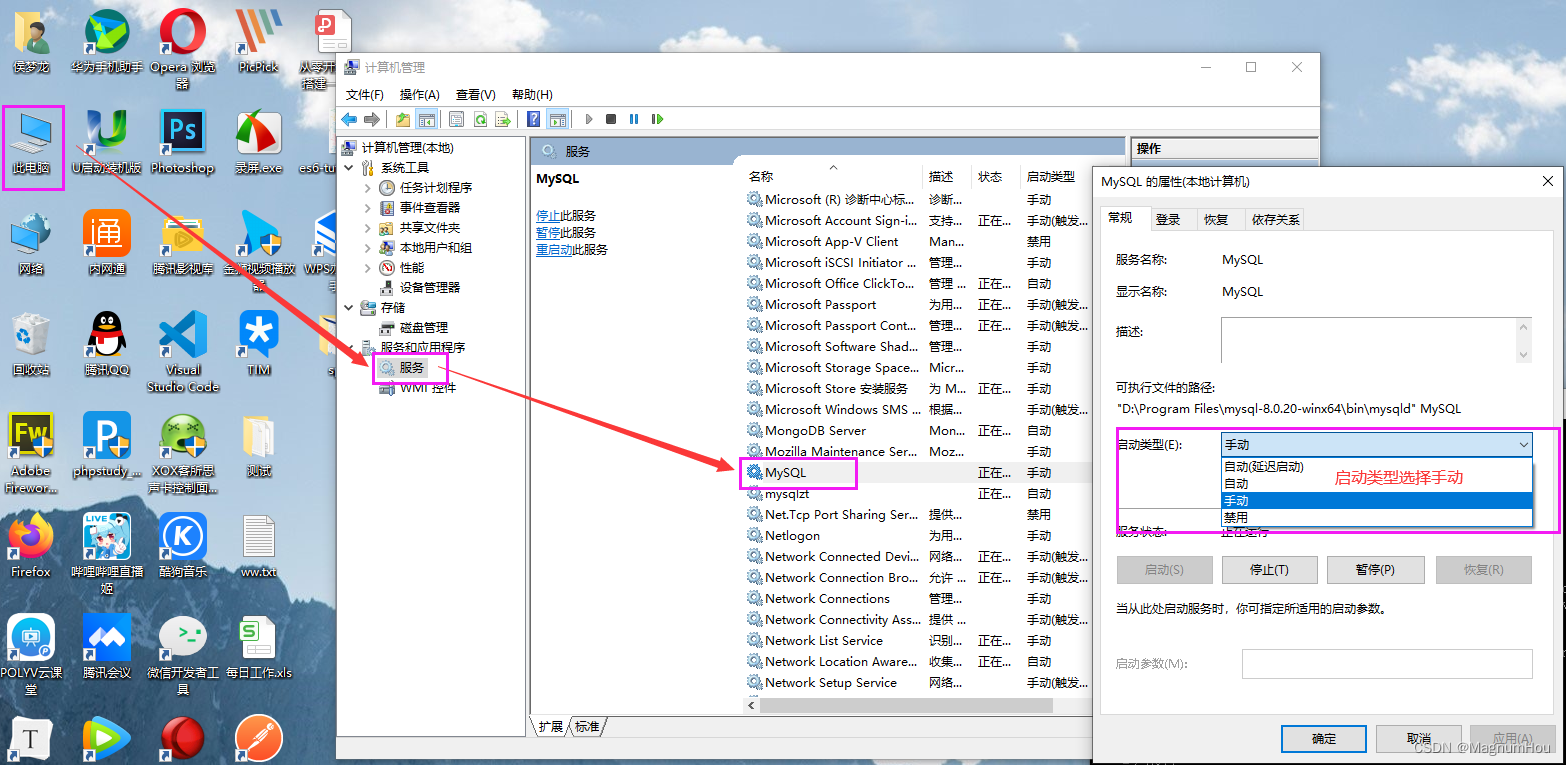
【数据库基础】Mysql下载安装及配置
下载 下载地址:https://downloads.mysql.com/archives/community/ 当前最新版本为 8.0版本,可以在Product Version中选择指定版本,在Operating System中选择安装平台,如下 安装 MySQL安装文件分两种 .msi和.zip [外链图片转存失…...

iptables安全与防火墙
防火墙 防火墙主要作用是隔离功能,它是部署在网络边缘或主机边缘;另外在生产中防火墙的主要作用是:决定哪些数据可以被外网访问以及哪些数据可以进入内网访问;顾名思义防火墙处于TCP协议中的网络层。 防火墙分类: 软…...

Linux 内核线程启动以及内核调用应用层程序
#include <linux/kthread.h> //内核线程头文件 static task_struct *test_task; test_task kthread_run(thread_function, NULL, "test_thread_name"); if(IS_ERR(test_task)) { pr_err("test_thread_name create fail\n"); } static int th…...
React+Typescript清理项目环境
上文 创建一个 ReactTypescript 项目 我们创建出了一个 React配合Ts开发的项目环境 那么 本文 我们先将环境清理感觉 方便后续开发 我们先来聊一下React的一个目录结构 跟我们之前开发的React项目还是有一些区别 public 主要是存放一些静态资源文件 例如 html 图片 icon之类的 …...

【linux学习】linux的模块机制
文章目录 前言模块的Hello World! 前言 Linux允许用户通过插入模块,实现干预内核的目的。一直以来,对linux的模块机制都不够清晰,因此本文对内核模块的加载机制进行简单地分析。 ref:https://www.cnblogs.com/fanzhidongyzby/p/…...

用 oneAPI 实现 AI 欺诈检测:一款智能图像识别工具
简介 虚假图像和视频日益成为社交媒体、新闻报道以及在线内容中的一大隐患。在这个信息爆炸的时代,如何准确地识别和应对这些虚假内容已经成为一个迫切的问题。为了帮助用户更好地辨别虚假内容,我开发了一款基于 oneAPI、TensorFlow 和 Neural Compress…...

云计算的发展前景怎么样
云计算是当前科技领域中最受关注的领域之一,它的出现改变了传统的计算模式,使得企业和个人能够更加便捷地访问和使用计算资源。随着云计算技术的不断发展,它的前景也变得更加光明。 以下是云计算的发展前景: 云计算的市场份额将继续增长:根据市场研究机构的报告,云计算的市场份…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...

【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅!
【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅! 🌱 前言:一棵树的浪漫,从数组开始说起 程序员的世界里,数组是最常见的基本结构之一,几乎每种语言、每种算法都少不了它。可你有没有想过,一组看似“线性排列”的有序数组,竟然可以**“长”成一棵平衡的二…...

《Offer来了:Java面试核心知识点精讲》大纲
文章目录 一、《Offer来了:Java面试核心知识点精讲》的典型大纲框架Java基础并发编程JVM原理数据库与缓存分布式架构系统设计二、《Offer来了:Java面试核心知识点精讲(原理篇)》技术文章大纲核心主题:Java基础原理与面试高频考点Java虚拟机(JVM)原理Java并发编程原理Jav…...

大模型——基于Docker+DeepSeek+Dify :搭建企业级本地私有化知识库超详细教程
基于Docker+DeepSeek+Dify :搭建企业级本地私有化知识库超详细教程 下载安装Docker Docker官网:https://www.docker.com/ 自定义Docker安装路径 Docker默认安装在C盘,大小大概2.9G,做这行最忌讳的就是安装软件全装C盘,所以我调整了下安装路径。 新建安装目录:E:\MyS…...
