【动态规划】回文串问题
文章目录
- 动态规划(回文串问题)
- 1. 回文子串
- 2. 最长回文子串
- 3. 回文串分割 IV
- 4. 分割回文串 ||
- 5. 最长回文子序列
- 6. 让字符串成为回文串的最小插入次数
动态规划(回文串问题)
1. 回文子串
题目链接
-
状态表示
f[i][j]表示 i 到 j 的子串当中是否是回文 -
状态转移方程

-
初始化
最初所有的内容都是0即可
-
填表
因为 i j 需要用 i + 1 来初始化,所以这个时候需要从下往上填表
-
返回值
返回整个dp 表里true 的数目就可以
AC代码:
class Solution
{
public:int countSubstrings(string s) {int n = s.size();vector<vector<bool>> dp(n, vector<bool>(n));int ret = 0;for (int i = n - 1; i >= 0; i--){for (int j = i; j < n; j++){if (s[i] == s[j]){dp[i][j] = i + 1 < j ? dp[i + 1][j - 1] : true;}if (dp[i][j]) ret++;}}return ret;}
};
2. 最长回文子串
题目链接
如果需要求一个字符串当中的最长的回文子串,需要将所有的回文子串找到,然后再所有的回文子串里面找打一个最长的就可以了
可以参考上一个题目回文子串
AC代码:
class Solution
{
public:string longestPalindrome(string s) {// 找到所有的回文子串int n = s.size();vector<vector<bool>> dp(n, vector<bool>(n));int begin = 0, len = 1;for (int i = n - 1; i >= 0; i--){for (int j = i; j < n; j++){if (s[i] == s[j]){dp[i][j] = i + 1 < j ? dp[i + 1][j - 1] : true;}if (dp[i][j] && j - i + 1 > len){begin = i;len = j - i + 1;}}}return s.substr(begin, len);}
};
3. 回文串分割 IV
题目链接
分析:如果暴力解题的话,i 和 j 可以把整个字符串分为3份,只需要遍历所有可能分为3份的情况直接判断是否都是回文串不就可以了。但是判断回文串需要花费时间,可以使用上面两道题的方法来判断是不是回文串
AC代码:
class Solution
{
public:bool checkPartitioning(string s) {int n = s.size();vector<vector<bool>> dp(n, vector<bool>(n));for (int i = n - 1; i >= 0; i--){for (int j = i; j < n; j++){if (s[i] == s[j]) dp[i][j] = i + 1 < j ? dp[i + 1][j - 1] : true;}}for (int i = 1; i < n - 1; i++){for (int j = i; j < n - 1; j++){if (dp[0][i - 1] && dp[i][j] && dp[j + 1][n - 1]) return true;}}return false;}
};
4. 分割回文串 ||
题目链接
-
状态表示
dp[i]表示0 到 i 之间,可以把所有子串都分割为回文串的最小次数 -
状态转移方程

-
初始化
所需初始位最大即可
-
填表
从左到右
-
返回值
AC代码:
class Solution
{
public:int minCut(string s) {int n = s.size();vector<vector<bool>> isPal(n, vector<bool>(n));for (int i = n - 1; i >= 0; i--){for (int j = i; j < n; j++){if (s[i] == s[j]) isPal[i][j] = i + 1 < j ? isPal[i + 1][j - 1] : true;}}vector<int> dp(n, INT_MAX);for (int i = 0; i < n; i++){if (isPal[0][i]) dp[i] = 0;else {for (int j = 1; j <= i; j++){if (isPal[j][i]) dp[i] = min(dp[i], dp[j - 1] + 1);}}}return dp[n - 1];}
};
5. 最长回文子序列
题目链接
-
状态表示
之前以某个位置为结尾来分析状态表示,如果dp[i]表示到i位置的最长回文子序列的长度来推导状态转移方程,只有长度是分析不出来状态转移方程。
dp[i][j]表示i j 这个区间内,最长的回文子序列的长度 -
状态转移方程
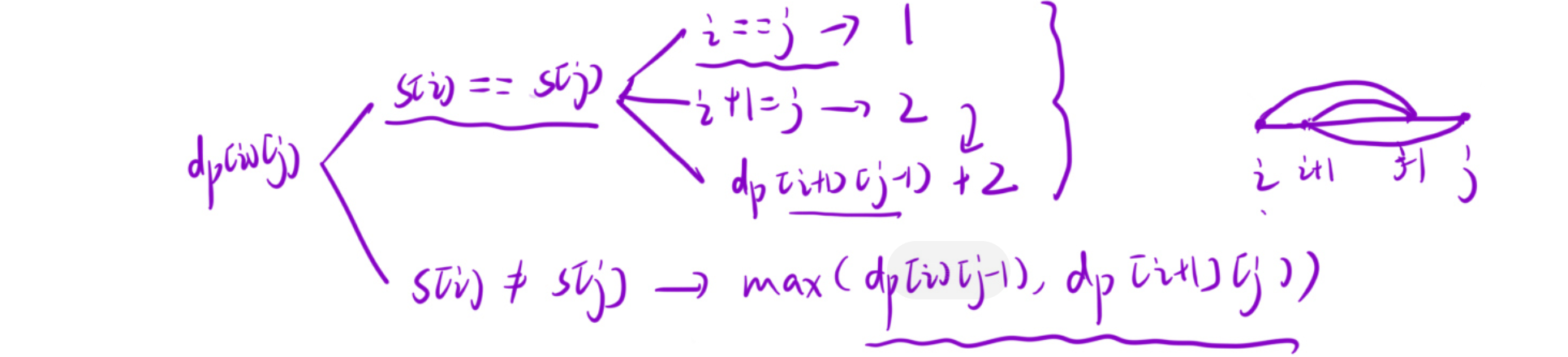
-
初始化
无需初始化
-
填表
因为需要用到 后面的值,所以填表需要从下到上,从左到右
-
返回值
AC代码:
class Solution
{
public:int longestPalindromeSubseq(string s) {int n = s.size();vector<vector<int>> dp(n, vector<int>(n));for (int i = n - 1; i >= 0; i--){for (int j = i; j < n; j++){if (s[i] == s[j]){dp[i][j] = i ==j ? 1 : dp[i + 1][j - 1] + 2;}else dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);}}return dp[0][n - 1];}
};
6. 让字符串成为回文串的最小插入次数
题目链接
-
状态表示
dp[i][j]表示:i 到 j 这个区间内,成为回文串的最小插入次数 -
状态转移方程
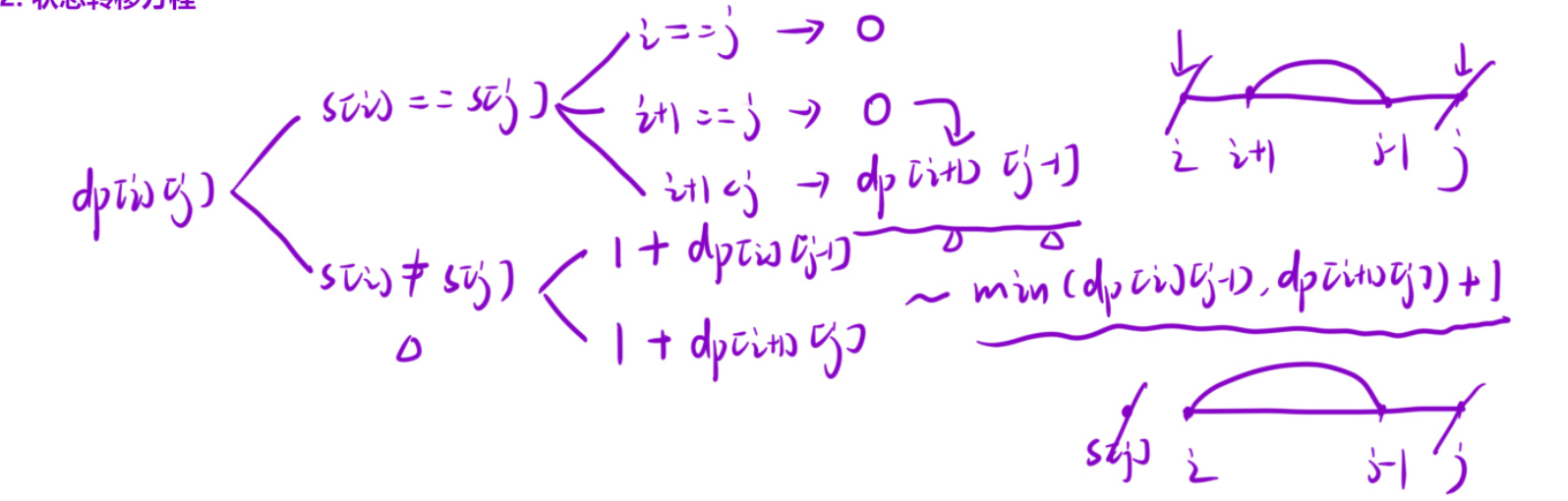
-
初始化
-
填表
从下往上,从左到右
-
返回值
AC代码:
class Solution
{
public:int minInsertions(string s) {int n = s.size();vector<vector<int>> dp(n, vector<int>(n));for (int i = n - 1; i >= 0; i--){for (int j = i; j < n; j++){if (s[i] == s[j]) dp[i][j] = i + 1 < j ? dp[i + 1][j - 1] : 0;else dp[i][j] = min(dp[i + 1][j], dp[i][j - 1]) + 1;}}return dp[0][n - 1];}
};
相关文章:
【动态规划】回文串问题
文章目录 动态规划(回文串问题)1. 回文子串2. 最长回文子串3. 回文串分割 IV4. 分割回文串 ||5. 最长回文子序列6. 让字符串成为回文串的最小插入次数 动态规划(回文串问题) 1. 回文子串 题目链接 状态表示 f[i][j]表示 i 到 j …...

Laravel Swift Mail发送带附件的邮件报错 “Swift_IoException The path cannot be empty“处理
先说下情况,就是我要做一个发送附件的邮件发送功能,结果,报错:The path cannot be empty。给我整的有点迷糊,网上也没有类似的问题。后来,我检查了一下代码,发现有个地方,是需要给附…...

Linux下常见的代理服务器软件介绍
在Linux系统中,代理服务器是我们搭建网络环境和处理网络请求的常用工具。但是,你知道Linux下常见的代理服务器软件有哪些吗?本文将为你带来对几款常见的Linux代理服务器软件的介绍,帮助你选择适合的代理服务器。 一、Squid&#…...
SCSS的基本用法
1、声明变量 $ 声明变量的符号 $ 下面这张图左半部分是scss的语法,右半部分是编译后的css。(整篇文章皆是如此) 2、默认变量 !default sass 的默认变量仅需要在值后面加上 !default 即可。 如果分配给变量的值后面添加了 !default 标志…...
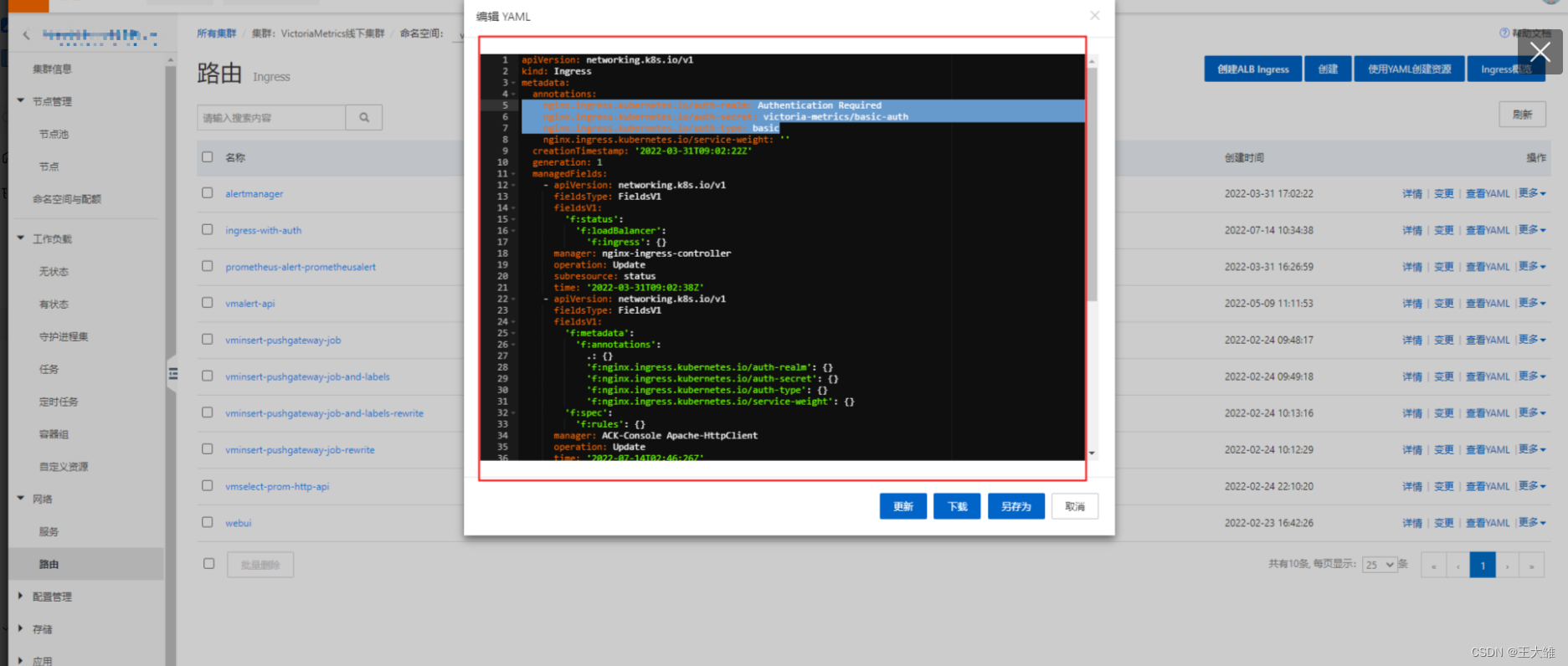
alertmanager创建nginx-ingress basic auth鉴权
步骤 生成密码 printf "admin:$(openssl passwd -crypt xxxxxx)\n" >> auth 创建新的 Kubernetes 密钥 kubectl create secret generic basic-auth --from-file auth -n victoria-metrics 修改 ingress 以使用 secret 中的凭证来实现基本身份验证 编辑 P…...
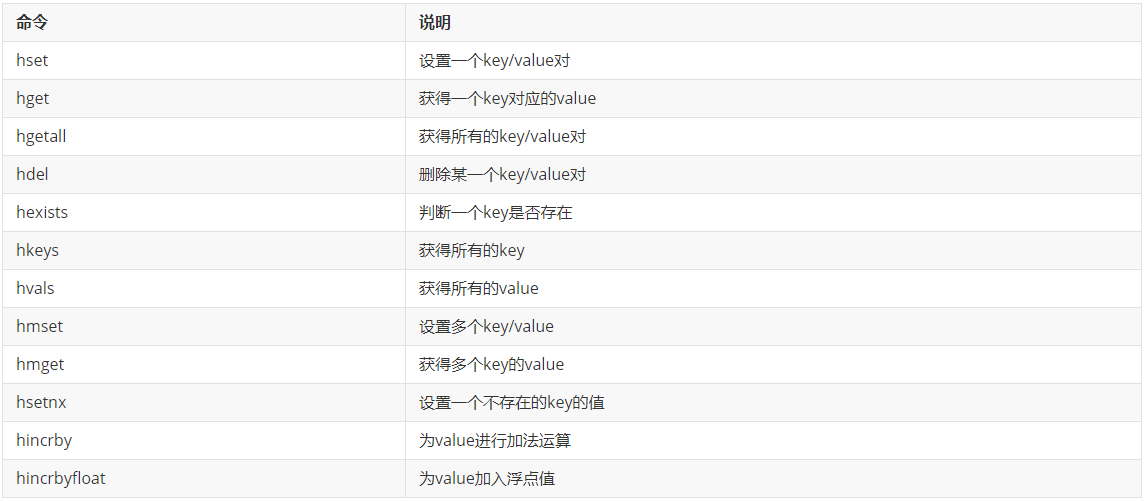
系列六、Redis中的五大数据类型及相关操作
一、五大数据类型 String类型、List类型、Set类型、ZSet类型、hash类型。 二、String类型 2.1、内存储存模型 2.2、常用操作命令 三、List类型 3.1、概述 list列表,相当于Java中的list集合。特点:元素有序 且 可以重复。 3.2、内存存储模型 3.3、常用…...
四大运营商的大流量卡测评,看完您会选哪个运营商?
很多朋友都说网上的流量卡资费是真的便宜,但是小编认为资费便宜归便宜,但是运营商的小心思也有不少。 今天小编就带大家看一看三大运营商推出的正规流量卡都有哪些小心思? 首先,移动推出的线上大流量卡数量是最少的ÿ…...
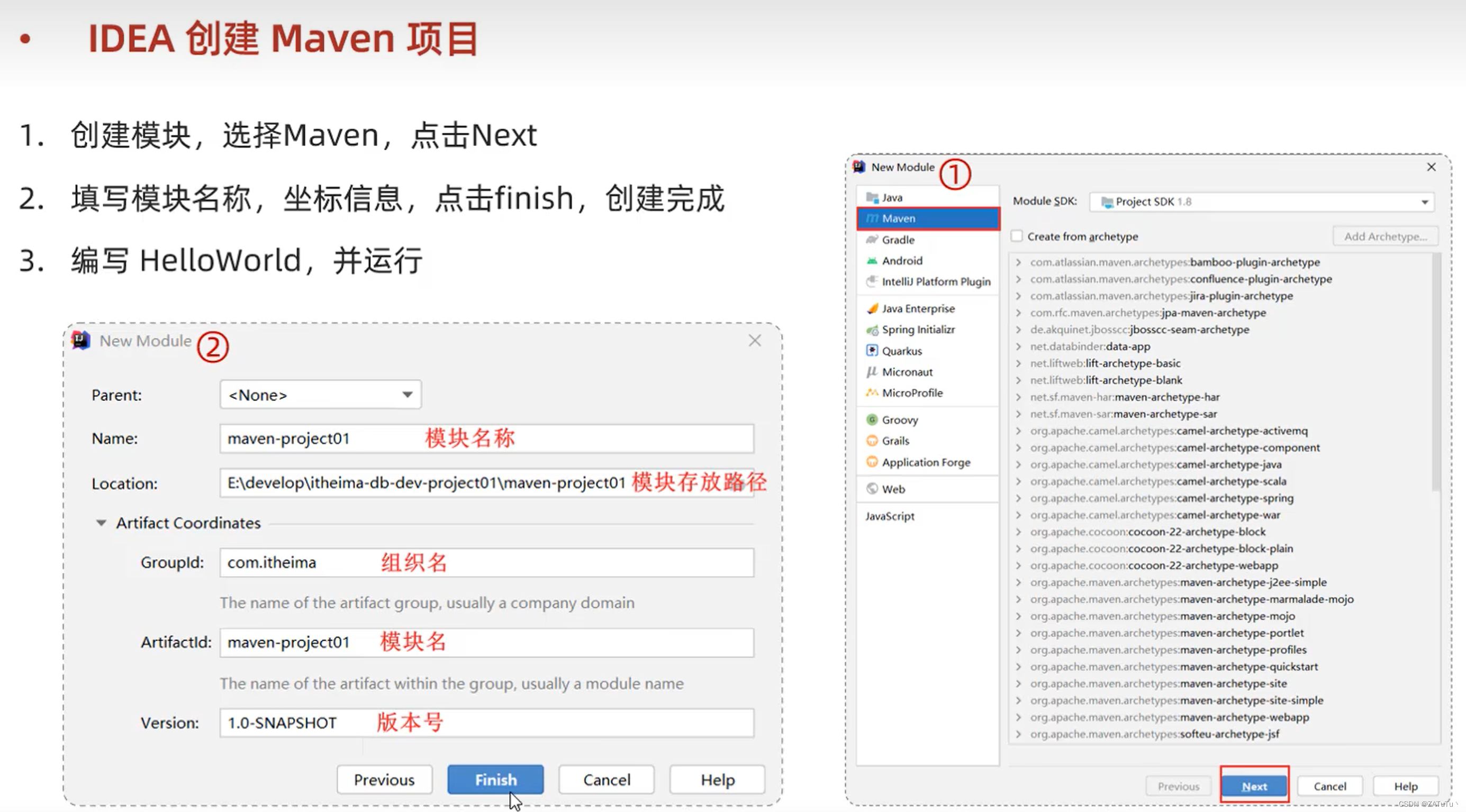
Apache-Maven
安装Maven 解压apache-maven到目录下 Maven目录如下 bin:目录中存放的是可执行文件,JAVA项目中的编译执行打包都要使用bin. conf:存放的是Maven的配置文件,本地配置、私服配置都需要在conf下的settings.xml进行配置。 lib下存放的是Maven所…...

什么是原子交换?
安全地在各个区块链网络之间传输资产对于释放被困流动性并吸引更多用户进入这一领域至关重要,同时也保持 Web3 的信任最小化核心价值。原子交换是一种让两个人在不依赖于中介来促成交易的情况下,在不同的区块链网络之间交换通证资产的方式。这为 DeFi 用…...

java springboot word文档转pdf
java springboot word文档转pdf 1、环境2、依赖3、代码 1、环境 1、java、springboot 2、maven或者gradle 3、办公软件(自己电脑上的wps或者office等,如果部署到服务器上也要安装,linux、Mac 都有,自己安装) 可能会遇…...

【Leetcode Sheet】Weekly Practice 2
Leetcode Test 1281 整数的各位积和之差(8.9) 给你一个整数 n,请你帮忙计算并返回该整数「各位数字之积」与「各位数字之和」的差。 提示: 1 < n < 10^5 【原始代码】: int subtractProductAndSum(int n){//1 < n < 10^5//…...
【BERTopic应用 03/3】:微调参数
一、说明 一般来说,BERTopic 在开箱即用的模型中工作得很好。但是,当您有数百万个数据要处理时,使用基本模型处理数据可能需要一些时间。在这篇文章中,我将向您展示如何微调BERTopic中的一些参数并比较它们的结果。让我们潜入。 二…...
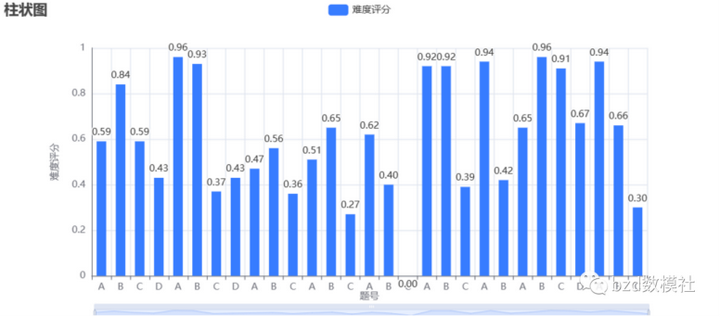
2023年上半年数学建模竞赛题目汇总与难度分析
2023年上半年数学建模竞赛题目汇总与难度分析 由于近年来国赛ABC题出题方式漂浮不定,没有太大的定性,目前总体的命题方向为,由之前的单一模型问题变为数据分析评价优化或者预测类题目是B、C题的主要命题方向。为了更好地把握今年命题的主方…...

Linux下搭建java环境
文章目录 一,xshell链接linux二,linux安装jdk环境 一,xshell链接linux 这里用到的工具,VMware搭配CentOS7 64位Xshell5 操作之前确保,传输Xshell连接了虚拟机 打开Xshell,文件->新建 主机ip—>进入虚拟机,右键打开终端,输入命令:ifco…...

String、StringBuffer、StringBuilder三者的异同?
String字符串 不可变的字符序列在 jdk1.8,我们底层用 char [ ] 存储在 jdk 17,我们底层用 byte [ ] 存储 StringBuffer字符串缓冲区类 可变的字符序列,线程安全的(synchronized),效率低在 jdk1.8…...

htmlCSS-----弹性布局案例展示
目录 前言 效果展示 编辑 代码 思路分析 前言 上一期我们学习了弹性布局,那么这一期我们用弹性布局来写一个小案例,下面看代码(上一期链接html&CSS-----弹性布局_灰勒塔德的博客-CSDN博客) 效果展示 代码 html代码&am…...

Fiddler模拟请求发送和修改响应数据
fiddler模拟伪造请求 方法一:打断点模拟HTTP请求 1、浏览器页面填好内容后(不要操作提交),打开fiddler,设置请求前断点,点击菜单fiddler,”Rules”\”Automatic Breakpoints”\”Before Requests” 2、在…...

RH850从0搭建Autosar开发环境【23】- Davinci Configurator之DCM实操实现DID的读取写入
配置DID 一、Developer中创建SWC1.1 创建Application Component Type1.2 实例化Component二、在SWC中创建接口以及Runnable2.1 创建DID的Service Ports2.2 创建DID的Service Runnable三、在Configurator连接接口以及生成代码3.1 连接DCM与SWC3.2 生成RTE3.3 生成SWC的DID的模板…...
ChatGPT收录
VSCode插件-ChatGPT 多磨助手 多磨助手 (domore.run) Steamship Steamship 免费合集 免费chatGPT - Ant Design Pro 免费AI聊天室 (xyys.one)...

Nginx随笔
Nginx下载链接 安装命令: apt update apt install nginx 一、基础命令(Ubuntu) 1、在全局 nginx -t //检查Nginx的配置文件是否有错 systemctl start nginx //启动Nginx systemctl stop nginx //停止Nginx systemctl status nginx //查…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...
