Java之动态规划之机器人移动
目录
0.动态规划问题
一.不同路径
1.题目描述
2.问题分析
3.代码实现
二.不同路径 II
1.题目描述
2.问题分析
3.代码实现
三.机器人双向走路
1.题目描述
2.问题分析
3.代码实现
0.动态规划问题
动态规划(Dynamic Programming)算法的核心思想是:将大问题划分为小问题,进行解决,从而一步步获取最优解的处理算法
动态规划对于解决最优子结构啊和重叠子问题等问题时候,有着很好的应用
对于动态规划问题,大致可以分为以下几步:
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组
一.不同路径
1.题目描述
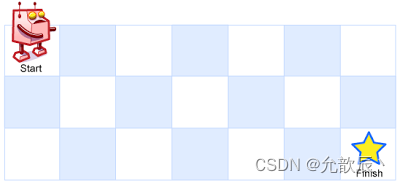
一个机器人位于一个
m x n网格的左上角 (起始点在下图中标记为 “Start” )。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
力扣:力扣
2.问题分析
1.确定dp数组(dp table)以及下标的含义
dp[i][j]:机器人走到(i,j)网格的位置有dp[i][j]种方法
2.确定递推公式
因为机器人每次只能向下或者向右移动,所以机器人到达(i,j)的位置只存在两种情况
第一种:从上边的格子走过来,一共有dp[i-1][j]种情况
第二种:从左边的格子走过来,一种有dp[i][j-1]种情况
所以dp[i][j]=dp[i-1][j]+dp[i][j-1]
3.dp数组如何初始化
由递推公式可以看出来,至少初始化第一行和第一列,因为机器人只能左走和下走,所以第一行和第一列只可能有一种情况到达(一直左走或者一直向下走)
4.确定遍历顺序
由递推公式可以看出来,从左到右,从上到下
5.举例推导dp数组
对m = 3, n = 7进行推导
[1, 1, 1, 1, 1, 1, 1]
[1, 2, 3, 4, 5, 6, 7]
[1, 3, 6, 10, 15, 21, 28]
3.代码实现
public int uniquePaths(int m, int n) {int[][] dp=new int[m][n];for(int i=0;i<n;i++){dp[0][i]=1;}for(int i=1;i<m;i++){dp[i][0]=1;}for(int i=1;i<m;i++){for(int j=1;j<n;j++){dp[i][j]=dp[i][j-1]+dp[i-1][j];}}return dp[m-1][n-1];}二.不同路径 II
1.题目描述
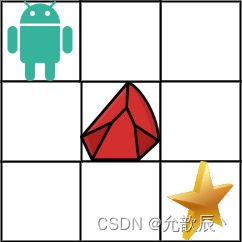
一个机器人位于一个
m x n网格的左上角 (起始点在下图中标记为 “Start” )。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
网格中的障碍物和空位置分别用
1和0来表示。
力扣:力扣
2.问题分析
这一题与上一题的区别就是多了障碍,有障碍的地方右走是无法到达的,但是可以从上方到达(不是第一行),知道这个易解
1.确定dp数组(dp table)以及下标的含义
dp[i][j]:机器人走到(i,j)网格的位置有dp[i][j]种方法
2.确定递推公式
因为机器人每次只能向下或者向右移动,所以机器人到达(i,j)的位置(左方不存在任何障碍)只存在两种情况
第一种:从上边的格子走过来,一共有dp[i-1][j]种情况
第二种:从左边的格子走过来,一种有dp[i][j-1]种情况
所以dp[i][j]=dp[i-1][j]+dp[i][j-1]
左方一格存在障碍的时候,只能从上方到来(默认障碍位置到达的方法dp[i][j]为0即可)
3.dp数组如何初始化
由递推公式可以看出来,至少初始化第一行和第一列,当右方存在障碍,第一行和第一列只可能有一种情况到达,当上方或者左方存在障碍的时候,障碍之后的路没有情况可以到达
for (int i = 0; i < m && obstacleGrid[i][0] == 0; ++i) {dp[i][0] = 1;}for (int i = 0; i < n && obstacleGrid[0][i] == 0; ++i) {dp[0][i] = 1;}4.确定遍历顺序
由递推公式可以看出来,从左到右,从上到下
5.举例推导dp数组
对obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]进行推导
[1, 1, 1]
[1, 0, 1]
[1, 1, 2]
3.代码实现
public int uniquePathsWithObstacles(int[][] obstacleGrid) {int m = obstacleGrid.length;int n = obstacleGrid[0].length;int[][] dp = new int[m][n];if(obstacleGrid[0][0] == 1)return 0;for (int i = 0; i < m && obstacleGrid[i][0] == 0; ++i) {dp[i][0] = 1;}for (int i = 0; i < n && obstacleGrid[0][i] == 0; ++i) {dp[0][i] = 1;}for (int i = 1; i < m; ++i) {for (int j = 1; j < n; ++j) {if (obstacleGrid[i][j] == 0)dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}}return dp[m-1][n-1];}三.机器人双向走路
1.题目描述
假设有排成一行的N个位置,记为1~N,(N>=2),开始时机器人在start位置,有如下约束
- 机器人在1位置,下一步只能走到2位置
- 机器人在N位置,下一步只能走到N-1位置
- 机器人在其他位置,下一步能走左边,也能走右边
求机器人从start位置经过k步到达target位置的方法数。
2.问题分析
这一题从二维变成了一维,显然是增加了难度的,因为可能存在在一个位置上来回移动的情况,所以dp数组和前几题有明显的的不一样,采用从后到前的推导方式,从target位置推导到start位置
1.确定dp数组(dp table)以及下标的含义
dp[i][j]的含义:机器人剩余j步,在i位置走到target位置可以有dp[i][j]中方法数
2.确定递推公式
因为机器人只能向左或是向右移动,所以dp[i][j]可以有两种方式推导出来
从左格移动到i位置:dp[i][j]=dp[i-1][j-1];
从右格移动到i位置:dp[i][j]=dp[i+1][j-1];
所以递推公式为:dp[i][j]=dp[i-1][j-1]+dp[i+1][j-1]
但是存在两种特殊情况,当机器人位于1位置的时候,只能向右移动到2位置
当机器人位于n位置的时候,只能向左移动到n-1位置
if (i == 1) {dp[i][j] = dp[2][j - 1];} else if (i == n) {dp[i][j] = dp[n - 1][j - 1];} else {dp[i][j] = dp[i + 1][j - 1] + dp[i - 1][j - 1];}3.dp数组如何初始化
当机器人剩余0步的时候,已经在target位置的时候,这种情况下到达dp显然是1中情况
4.确定遍历顺序
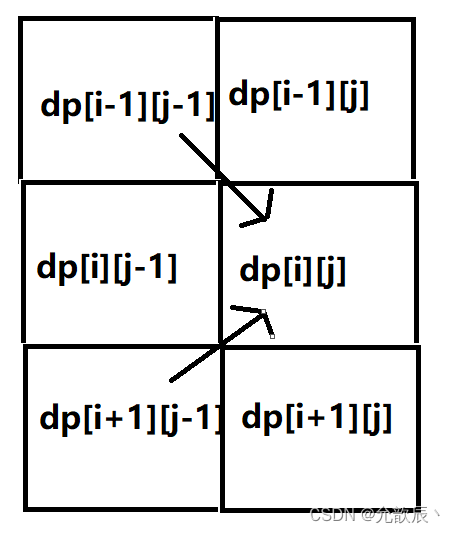
由下图可以看出,遍历顺序应该先从左到右,然后从上到下进行遍历,也就是j(剩余的步数)在外层循环,i(机器人目前的位置)在内存循环
5.举例推导dp数组
对n=5,steps=3,start=2,target=3进行推导
[0, 1, 0, 2] [1, 0, 2, 0] [0, 1, 0, 3] [0, 0, 1, 0] [0, 0, 0, 1]
也就是这三种情况
1).2->1,1->2,2->3 2).2->3,3->2,2->3 3).2->3,3->4,4->3
3.代码实现
public int move(int n, int steps, int start, int target) {int[][] dp = new int[n + 1][steps + 1];//剩余的步数为0,当前位置为target时dp[target][0] = 1;for (int j = 1; j <= steps; ++j) {for (int i = 1; i <= n; ++i) {if (i == 1) {dp[i][j] = dp[2][j - 1];} else if (i == n) {dp[i][j] = dp[n - 1][j - 1];} else {dp[i][j] = dp[i + 1][j - 1] + dp[i - 1][j - 1];}}}return dp[start][steps];}回溯代码
/*** @param n 能够到达位置的最大值(1--n位置移动)* @param steps 剩余需要移动的步数* @param start 当前开始所处的位置* @param target 需要到达的目标位置* @return 一共到达目标位置的方法数*/public int move(int n, int steps, int start, int target) {if (steps == 0) {if (start == target) {return 1;} elsereturn 0;} else if (start == 1) {return move(n, steps - 1, 2, target);} else if (start == n) {return move(n, steps - 1, n - 1, target);} else {return move(n, steps - 1,start + 1, target) + move(n, steps - 1, start - 1, target);}}相关文章:

Java之动态规划之机器人移动
目录 0.动态规划问题 一.不同路径 1.题目描述 2.问题分析 3.代码实现 二.不同路径 II 1.题目描述 2.问题分析 3.代码实现 三.机器人双向走路 1.题目描述 2.问题分析 3.代码实现 0.动态规划问题 动态规划(Dynamic Programming)算法的核心思想是:将大问题划分为小问…...
seata源码-全局事务提交 服务端源码
前面的博客中,我们介绍了,发起全局事务时,是如何进行全局事务提交的,这篇博客,主要记录,在seata分布式事务中,全局事务提交的时候,服务端是如何进行处理的 发起全局事务提交操作 事…...
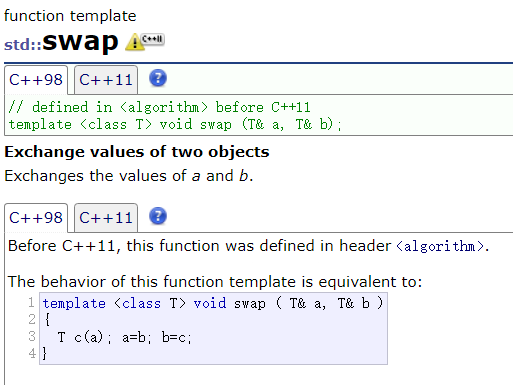
C++ 模板
文章目录一、泛型编程二、 函数模板三、类模板一、泛型编程 泛型编程:编写与类型无关的通用代码,代码复用的一种方法 在 C 中,我们可以通过函数重载实现通用的交换函数 Swap ,但是有一些缺点 重载函数只有类型不同,…...
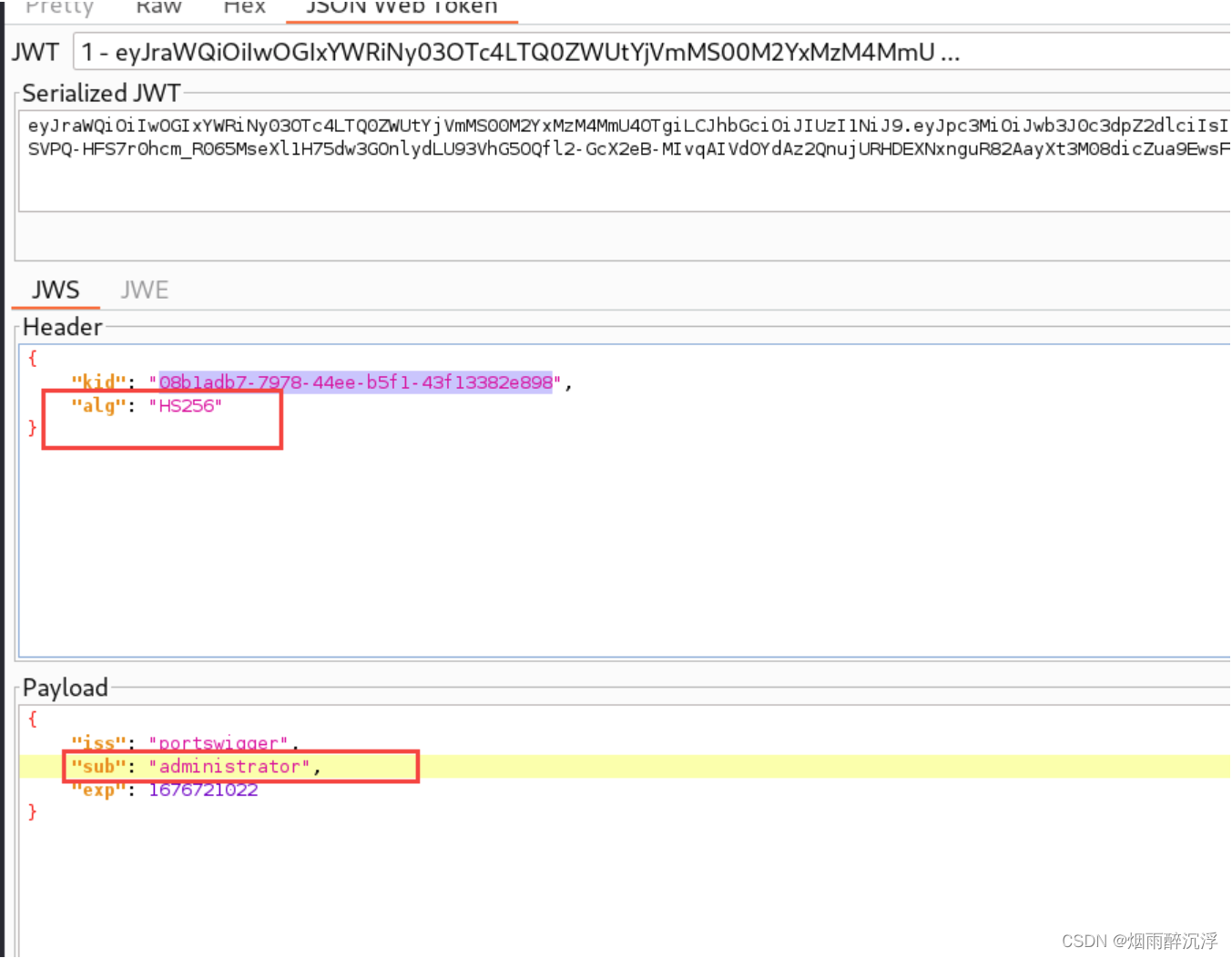
JWT安全漏洞以及常见攻击方式
前言 随着web应用的日渐复杂化,某些场景下,仅使用Cookie、Session等常见的身份鉴别方式无法满足业务的需要,JWT也就应运而生,JWT可以有效的解决分布式场景下的身份鉴别问题,并且会规避掉一些安全问题,如CO…...
)
华为OD机试题 - 最小施肥机能效(JavaScript)
最近更新的博客 华为OD机试题 - 任务总执行时长(JavaScript) 华为OD机试题 - 开放日活动(JavaScript) 华为OD机试 - 最近的点 | 备考思路,刷题要点,答疑 【新解法】 华为OD机试题 - 最小步骤数(JavaScript) 华为OD机试题 - 任务混部(JavaScript) 华为OD机试题 - N 进…...
Python(1)变量的命名规则
目录 1.变量的命名原则 3.内置函数尽量不要做变量 4.删除变量和垃圾回收机制 5.结语 参考资料 1.变量的命名原则 ①由英文字母、_(下划线)、或中文开头 ②变量名称只能由英文字母、数字、下画线或中文字所组成。 ③英文字母大小写不相同 实例: 爱_aiA1 print(…...
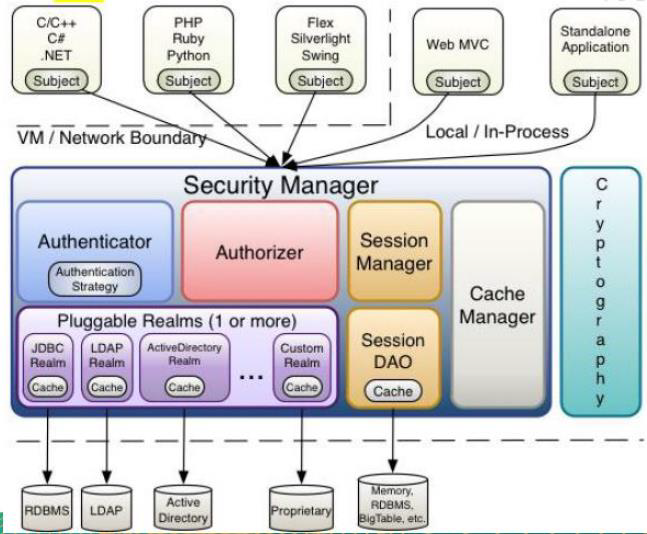
Shiro1.9学习笔记
文章目录一、Shiro概述1、Shiro简介1.1 介绍1.2 Shiro特点2、Shiro与SpringSecurity的对比3、Shiro基本功能4、Shiro原理4.1 Shiro 架构(外部)4.2 shiro架构(内部)二、Shiro基本使用1、环境准备2、登录认证2.1 登录认证概念2.2 登录认证基本流程2.3 登录认证实例2.4 身份认证源…...
2.5|iot|嵌入式Linux系统开发与应用|第4章:Linux外壳shell脚本程序编程
1.shell基础 Shell是Linux操作系统内核的外壳,它为用户提供使用操作系统的命令接口。 用户在提示符下输入的每个命令都由shell先解释然后发给Linux内核,所以Linux中的命令通称为shell命令。 通常我们使用shell来使用Linux操作系统。Linux系统的shell是…...

九龙证券|连续七周获加仓,四大行业成“香饽饽”!
本周17个申万职业北上资金持股量环比增加。 北上资金抢筹铝业龙头 本周A股商场全体冲高回落,沪指收跌1.12%,深成指跌2.18%,创业板指跌3.76%。北上资金周内小幅净流入。在大盘体现较差的周四周五,北上资金别离逆市回流67.94亿元、…...
210天从外包踏进华为跳动那一刻,我泪目了
前言 没有绝对的天才,只有持续不断的付出。对于我们每一个平凡人来说,改变命运只能依靠努力幸运,但如果你不够幸运,那就只能拉高努力的占比。 2021年4月,我有幸成为了华为的一名高级测试工程师,正如标题所…...

CMake 引入第三方库
CMake 引入第三方库 在 CMake 中,如何引入第三方库是一个常见的问题。在本文中,我们将介绍 CMake 中引入第三方库的不同方法,以及它们的优缺点。 1. 使用 find_package 命令 在 CMake 中,使用 find_package 命令是最简单和最常…...

软考中级-面向对象
面向对象基础(1)类类分为三种:实体类(世间万物)、接口类(又称边界类,提供用户与系统交互的方式)、控制类(前两类之间的媒介)。对象:由对象名数据&…...

Linux 系统构成:bootloader、kernel、rootfs
写在前面: 本文章旨在总结备份、方便以后查询,由于是个人总结,如有不对,欢迎指正;另外,内容大部分来自网络、书籍、和各类手册,如若侵权请告知,马上删帖致歉。 目录前言bootloaderk…...
SpringCloud - Eureka注册发现
目录 提供者与消费者 Eureka原理分析 搭建Eureka服务 服务注册 服务发现 提供者与消费者 服务提供者: 一次业务中,被其它微服务调用的服务(提供接口给其它微服务)服务消费者: 一次业务中,调用其它微服务的服务(调用其它微服务…...
WampServer安装教程
文章目录简介:官网地址安装步骤:我是阿波,学习PHP记录一下笔记,如果对你有帮助,欢迎一键三连,谢谢! 简介: WampServer是一个用于Windows操作系统的Web开发环境,其名称来…...

Go语言泛型基础
泛型 Go 并不是一种静止的、一成不变的编程语言。新的功能是在经过大量的讨论和实验后慢慢采用的。最初的 Go1.0发布以来,Go语言习惯的模式已经发生了重大变化1.7的context、1.11的modules、1.13 error嵌套等Go的 1.18 版本包括了类型参数的实现,也就是…...

基于android的中医养生app
需求信息: 中医健康养生APP分为四大模块,其中个人中心又分为4大块,游客用户个人中心是空白的。 上图为养生知识推广普及模块的功能结构图。 在养生知识推广普及模块界面,用户可以选择自己感兴趣的模块进行文章浏览,文章…...

2023美赛C代码思路结果【全部更新完毕】注释详尽
C题已完成全部代码,注释详尽,并增加扰动项,保证大家的结果不会撞 需要全部问题的可以点击:https://www.jdmm.cc/file/2708697/ 下面贴出核心代码: -- coding: utf-8 -- TODO: 入口函数 import numpy as np from…...
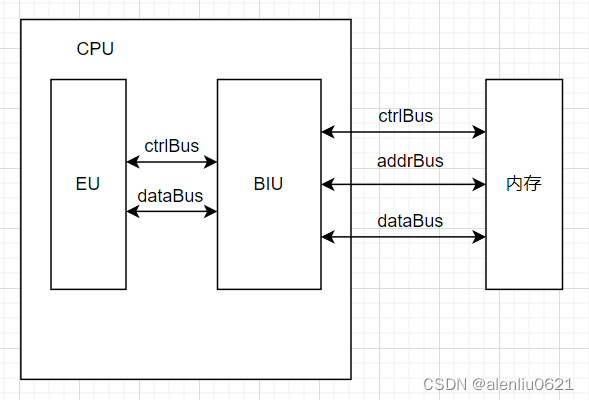
实现8086虚拟机(二)——模拟CPU和内存
文章目录CPU 架构EU(执行单元)BIU(总线接口单元)小结一下模拟内存模拟 BIU模拟 EU模拟 CPU总结要模拟 8086 CPU 运行,必须知道 CPU 的一些知识。下文的知识点都来自《Intel_8086_Family_Users_Manual 》。CPU 架构 微…...
Windows7下使用VMware11.1.1安装ubuntu-16.04.7
一、说明二、安装说明三、安装步骤详解1、先安装VMware软件2、创建虚拟机3、编辑虚拟机4、开启虚拟机,初始化Linux系统一、说明 虽然VMware和ubuntu最新版已经很高了,我这电脑由于是win7配值还低,所以采用低版本来安装 VMware版本࿱…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...
