5.利用matlab完成 符号矩阵的转置和 符号方阵的幂运算(matlab程序)
1.简述
Matlab符号运算中的矩阵转置
转置向量或矩阵
B = A.'
B = transpose(A)
说明
B = A.' 返回 A 的非共轭转置,即每个元素的行和列索引都会互换。如果 A 包含复数元素,则 A.' 不会影响虚部符号。例如,如果 A(3,2) 是 1+2i 且 B = A.',则元素 B(2,3) 也是 1+2i。
B = transpose(A) 是执行 A.' 的另一种方式,它可以为类启用运算符重载。
复共轭转置运算符 A' 还对 A 中复数元素的虚部符号求反。
两个命令效果相同,注意第一个命令加个“.”。而平时实数矩阵常用A'来转置,这是共轭转置,对实数操作体现不出差异,而对虚数就出现差异了。
对于符号运算中,进行矩阵或向量转置时,共轭转置命令会是转置后矩阵内为"conj(a)",从而无法继续符号运算。
2.代码
%% 学习目标:matlab符号矩阵的转置
clear all;
A1=sym(magic(4))
B1=A1' %如果是复数则为共轭转置
C1=A1.' %真正的转置
A2=sym([6+6i,6;6-6i,6])
B2=A2'
C2=A2.'
%% 学习目标:matlab符号方阵的幂运算
clear all;
a=sym('[x 4*x 4;4 4 x;4.0 x 4]')
y1=a^2
b=sym('[4 8;4 7]')
y2=2^b
3.运行结果


相关文章:

5.利用matlab完成 符号矩阵的转置和 符号方阵的幂运算(matlab程序)
1.简述 Matlab符号运算中的矩阵转置 转置向量或矩阵 B A. B transpose(A) 说明 B A. 返回 A 的非共轭转置,即每个元素的行和列索引都会互换。如果 A 包含复数元素,则 A. 不会影响虚部符号。例如,如果 A(3,2) 是 12i 且 B A.࿰…...

为什么要自动化Web测试?
Web自动化是更快地实现所需结果的较佳方式。自动化测试在市场上引起了巨大的轰动。此软件测试过程可以让您使用正确的自动化测试工具和技术集自动执行测试过程。我们执行它是为了检查软件应用程序是否具有完全按照我们希望它执行的方式执行的勇气。 比以往更快地获得反馈 自动化…...

Spark_RDD的容错机制_数据丢失恢复
我们都知道Spark是弹性分布式数据集,数据会存储在多台机器上,那么如何确保在分布式数据计算中,数据不丢失就是其中的关键的部分。本文主要讲解一下Spark中的容错机制。 Spark 主要提供了3个层面的数据容错机制。分别是 调度层,RDD…...

VB+SQL期刊信息管理系统设计与实现
摘 要 本次毕业设计课题为“期刊信息管理系统”,该系统在正常运营中总是面对大量的读者信息、期刊信息以及两者相互作用产生的借刊信息,还刊信息。因此需要对读者资源、期刊资源、借刊信息、还刊信息进行管理,及时了解各个环节中信息的变更,有利于提高管理效率。 此次毕…...

如何在iPhone手机上修改手机定位和模拟导航?
如何在iPhone手机上修改手机定位和模拟导航? English 首先,你需要在Mac电脑上下载安装 Location Simulator/定位模拟工具 和 Runner 这两款应用程序。 完成安装后,打开软件,并用USB连接手机设备 修改iPhone手机定位和模拟导航 …...

Linux 当fork在for循环中的问题
以下代码会打印几个"A"? 例1.代码如下: int main(int argc, char* argv[],char* envp[]) { for(int i 0;i < 2; i ) { fork(); printf("A\n"); } exit(0); } 代码分析: //父进程for(int i …...
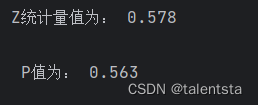
推断统计中非参数检验之卡方检验、列联表分析和游程检验
一、(卡方检验):赛马比赛的赛道会影响成绩吗 这里以一个实例赛马比赛的赛道是否会影响成绩为例,实际就是检验获胜频数与期望频数之间有无显著性差异。 import pandas as pdstep1 调用包 from scipy.stats import chisquare impor…...

AI社交来了,百度、Soul“双向奔赴”
随着科技的飞速进步和迅猛发展,AI技术已经开始渗透到教育、工作、社交、娱乐和健康多个领域,并为人们生活中的多个场景带来了诸多的创新和可能性。甚至可以说,AI技术已经深刻地介入到了我们日常生活的方方面面,让我们的生活方式发…...
【【verilog 典型电路设计之加法器树乘法器】】
verilog 典型电路设计之加法器树乘法器 加法器树乘法器 加法器树乘法器的设计思想是“移位后加”,并且加法运算采用加法器树的形式。乘法运算的过程是,被乘数与乘数的每一位相乘并且乘以相应的权值,最后将所得的结果相加,便得到了…...

选择最适合自己的NIO, 一探流技术
目录 一、Channel1、FileChannel代码示例2、DatagramChannel代码示例3、SocketChannel 和 ServerSocketChannel代码示例 二、Buffer1、ByteBuffer示例代码2、CharBuffer示例代码3、ShortBuffer、IntBuffer、LongBuffer、FloatBuffer、DoubleBuffer 等示例代码 三、Selector1、S…...
---socket网络控制线程封装)
智能家居(3)---socket网络控制线程封装
封装socket网络线程实现对智能家居中各种灯光的控制 main.Pro(主函数) #include <stdio.h> #include "controlDevice.h" #include "inputCommand.h" #include <pthread.h>struct Devices *pdeviceHead NULL; //设备工厂链表…...

ubuntu 安装 emscripten 时 install latest 安装报错问题
学习官网参考:Compiling a New C/C Module to WebAssembly - WebAssembly | MDN (mozilla.org) 报错信息 形如: Error: Downloading URL https://storage.googleapis.com/webassembly/emscripten-releases-builds/linux/b90507fcf011da61bacfca613569…...
concrt140.dll丢失怎么恢复?教你5种修复方法
首先介绍一下concrt140.dll是什么 concrt140.dll是Microsoft Visual C Redistributable for Visual Studio 2015所需的一个动态链接库文件。它是用于支持C程序运行的重要组件之一。当系统中缺少或丢失concrt140.dll文件时,可能会导致一些程序无法正常运行。 首先&a…...

【Vue-Router】路由入门
路由(Routing)是指确定网站或应用程序中特定页面的方式。在Web开发中,路由用于根据URL的不同部分来确定应用程序中应该显示哪个内容。 构建前端项目 npm init vuelatest //或者 npm init vitelatest安装依赖和路由 npm install npm instal…...

蓝牙耳机运动耳机哪个好、好用的运动蓝牙耳机推荐
如今的蓝牙耳机已经成为手机的最佳伴侣,也是运动爱好者的必备装备。然而,在众多蓝牙耳机中做出选择可能会让人感到困惑。其实,在选购运动蓝牙耳机时需要注意的事项还挺多的,比如舒适度、稳定性和音质等多个方面,逐一对照这些要点来…...

大数据面试题:Kafka的ISR机制
面试题来源: 《大数据面试题 V4.0》 大数据面试题V3.0,523道题,679页,46w字 可回答:1)从ISR踢出去之后呢;2)一般Leader怎么判断Follower挂掉? 参考答案: …...

Windows:解决MySQL登录ERROR 1045 (28000): Access denied for user ‘root‘@‘localhost‘ (using passwor=YES)问题
我在下载的MySQL是8.0.32版本,刚下的时候没什么问题第二天启动MySQL服务就出现了 ERROR 1045 (28000): Access denied for user rootlocalhost (using password: YES) 或 ERROR 1045 (28000): Access denied for user rootlocalhost (using password: NO) 这样的问题…...
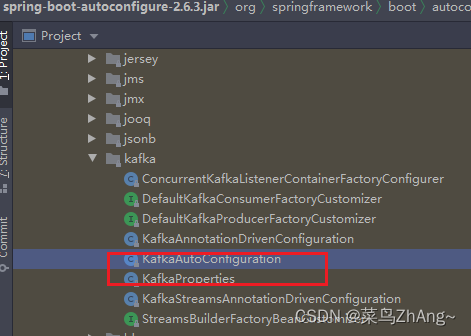
springboot整合kafka多数据源
整合kafka多数据源 项目背景依赖配置生产者消费者消息体 项目背景 在很多与第三方公司对接的时候,或者处在不同的网络环境下,比如在互联网和政务外网的分布部署服务的时候,我们需要对接多台kafka来达到我们的业务需求,那么当kafk…...
基于CentOS 7 配置nginx负载均衡
搭建负载均衡服务的需求如下: 1 ) 把单台计算机无法承受的大规模并发访问或数据流量分担到多台节点设备上,分别进行处理, 减少用户等待响应的时间, 提升用户体验。 2 ) 单个重负载的运算分担到多台节点设备上做并行处理ÿ…...

WordToPDF2.java
用Java将Word转PDF 本例子测试了spire.doc.free-3.9.0.jar的包 <dependency><groupId> e-iceblue </groupId><artifactId>spire.doc.free</artifactId><version>3.9.0</version></dependency> package word;import com.spire.…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...

Xela矩阵三轴触觉传感器的工作原理解析与应用场景
Xela矩阵三轴触觉传感器通过先进技术模拟人类触觉感知,帮助设备实现精确的力测量与位移监测。其核心功能基于磁性三维力测量与空间位移测量,能够捕捉多维触觉信息。该传感器的设计不仅提升了触觉感知的精度,还为机器人、医疗设备和制造业的智…...
