关于onload事件
onload事件是在网页中的所有内容(包括图片、样式表、脚本等)都加载完成后触发的事件。它常用于在页面加载完成后执行一些操作,例如初始化页面元素、绑定事件监听器等。
可以通过以下方式来使用onload事件:
在HTML标签中直接添加onload属性,指定要执行的JavaScript代码:
<body onload="myFunction()">
使用JavaScript的addEventListener方法来添加事件监听器:
window.addEventListener('load', myFunction);
在这两种方式中,myFunction是一个自定义函数,代表在页面加载完成后要执行的操作。
需要注意的是,如果在页面中同时使用了多个onload事件,它们将按照添加的顺序依次执行。因此,如果有多个函数需要在页面加载完成后执行,可以将它们按顺序添加到onload事件中。
此外,还可以通过JavaScript的window.onload属性来指定onload事件的处理函数,但要注意这种方式只能添加一个处理函数,且会覆盖掉之前绑定的任何onload事件处理函数。
相关文章:

关于onload事件
onload事件是在网页中的所有内容(包括图片、样式表、脚本等)都加载完成后触发的事件。它常用于在页面加载完成后执行一些操作,例如初始化页面元素、绑定事件监听器等。 可以通过以下方式来使用onload事件: 在HTML标签中直接添加…...
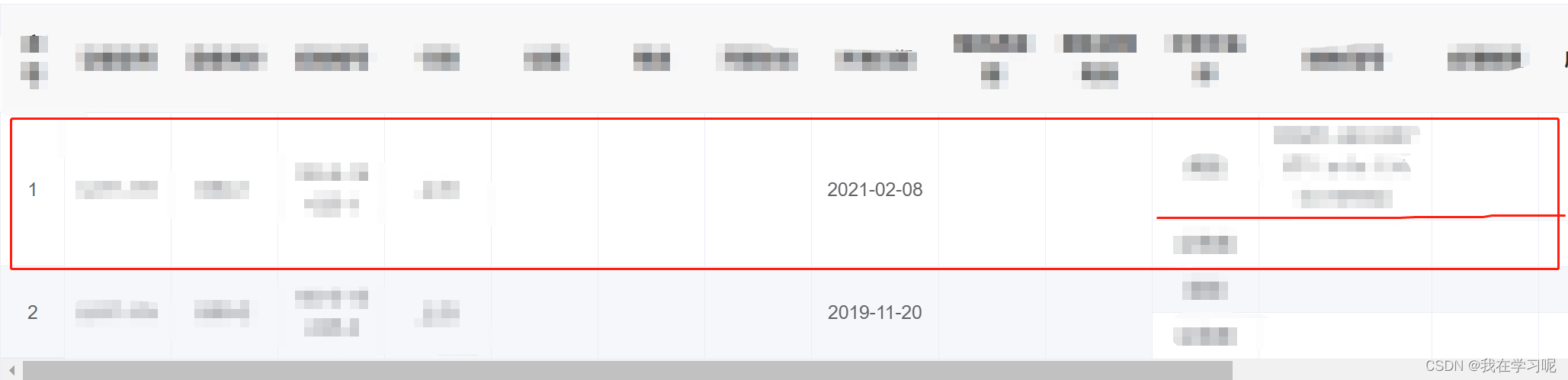
合并单元格
需求: 合并 相同名称的产品 先说下elementUI合并单元格的方法,先计算好要合并的行数rowspan,return {rowspan,colspan},其他的单元格return{0,0} getData(params) {//临时数组,存放产品名称相同的数量this…...
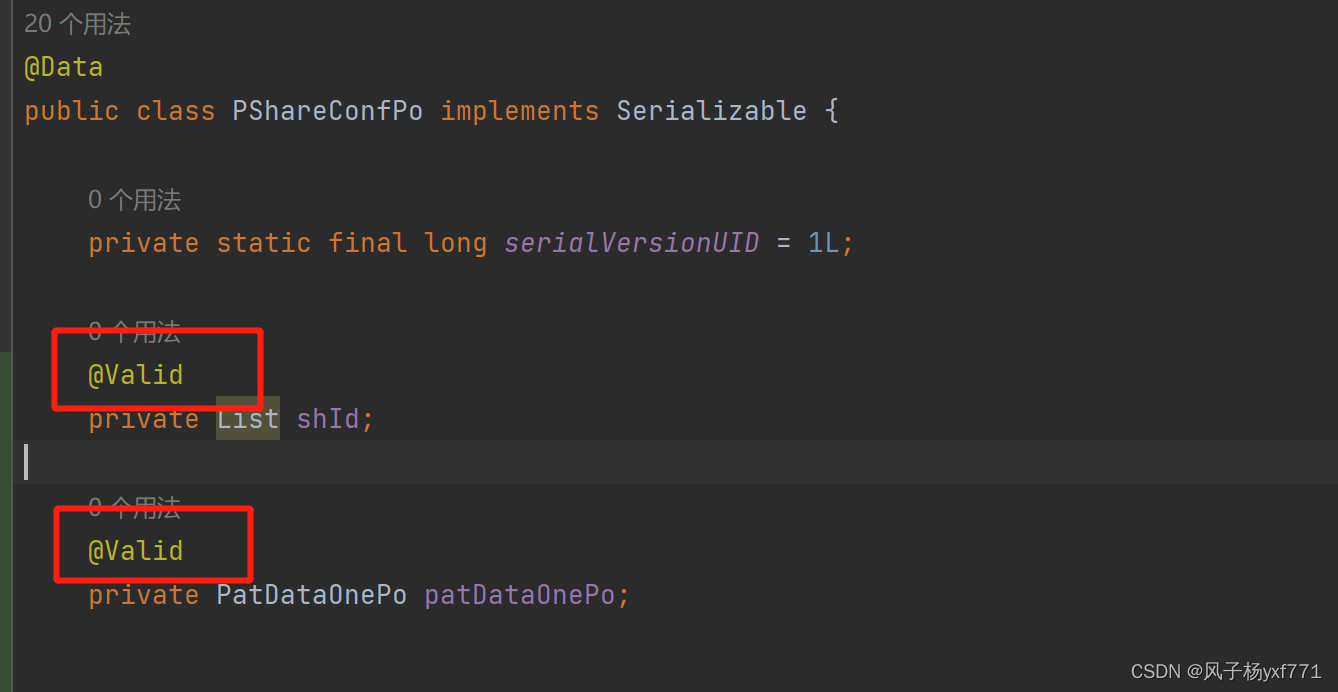
Spring Boot @Validated 验证注解的使用
1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-validation</artifactId> </dependency> 2、使用 2.1、非对象参数 参数如果是非对象格式,需要在controller类上面添…...

如何理解“对矩阵进行初等行变换不改变其列向量的线性关系”?
对矩阵A进行初等行变换相当于左乘一个可逆矩阵P。 把A看作是列向量组,若有Ax0,则其中的x就说明了列向量的线性关系: [ α 1 , α 2 , α 3 ] [ x 1 x 2 x 3 ] [ 0 ] \left[ \alpha_1 ,\alpha_2, \alpha_3 \right] \begin{bmatrix} x_1\\ x…...
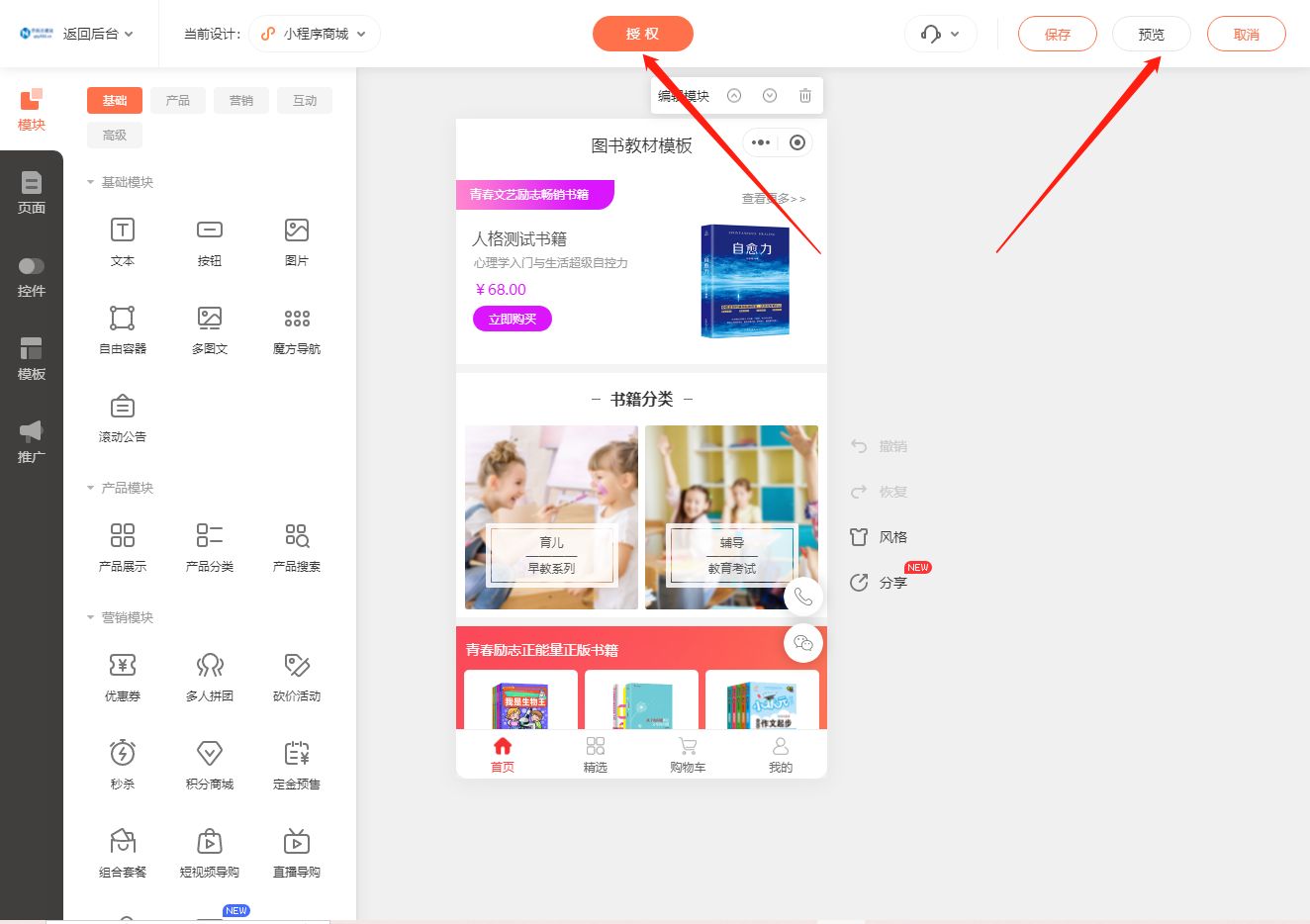
书店行业小程序开发攻略
随着移动互联网的快速发展,小程序成为了各行各业的热门选择,包括书店行业。书店小程序的开发可以为书店提供在线销售渠道,提高销售额,增强用户粘性。本文将介绍如何从搭建到上线开发一款书店行业小程序。 首先,我们需要…...

情感分析工具: TextBlob 与 VADER 的对比
一、说明 在本文我们将看到,在情感分析方面,我们更喜欢哪个库。这取决于很多情况。例如。数据采集。在我们进行分析之前,让我们先看看这两个库是关于什么的。 二、亮相工具库 2.1. 工具库TextBlob介绍: 图像。TextBlob: Simplif…...

uft8和utf8mb4的区别
文章目录 1、Unicode字符集2、UTF-8 编码3、utf8mb3 字符集4、utf8mb4 字符集5、utf8mb3和utf8mb4的区别 1、Unicode字符集 Unicode(统一码、万国码、单一码)是计算机科学领域里的一项业界标准,包括字符集、编码方案等。Unicode 是为了解决传…...

针对低分辨率或小目标的卷积-SPDConv
针对低分辨率或小目标的卷积-SPDConv 摘要引言A New Building Block:SPD-Conv附录代码: 摘要 卷积神经网络在许多计算机视觉任务中取得了巨大成功。然而,在图像低分辨率或目标较小任务上,他们的性能迅速下降。在本文中,我们指出&…...

vue基础-vue监听当前屏幕大小做不同的操作
文章目录 前言一、代码如下:总结 前言 在vue项目开发过程中,有个需求,就是当屏幕大于1024时,我们默认为PC模式。小于1024时,我们默认为H5模式。但是有的界面我们想在PC和H5上面展示不同的数据,请求不同的接…...

Unity框架学习--3
单例模式基类 构造函数私有化,防止外部创建对象 提供一个属性给外部访问,这个属性就相当于是这个类的唯一对象 分为懒汉模式和饿汉模式 不继承MonoBehaviour的单例模式 public static MyUiManager Instance {get{if (instance null){instance new …...
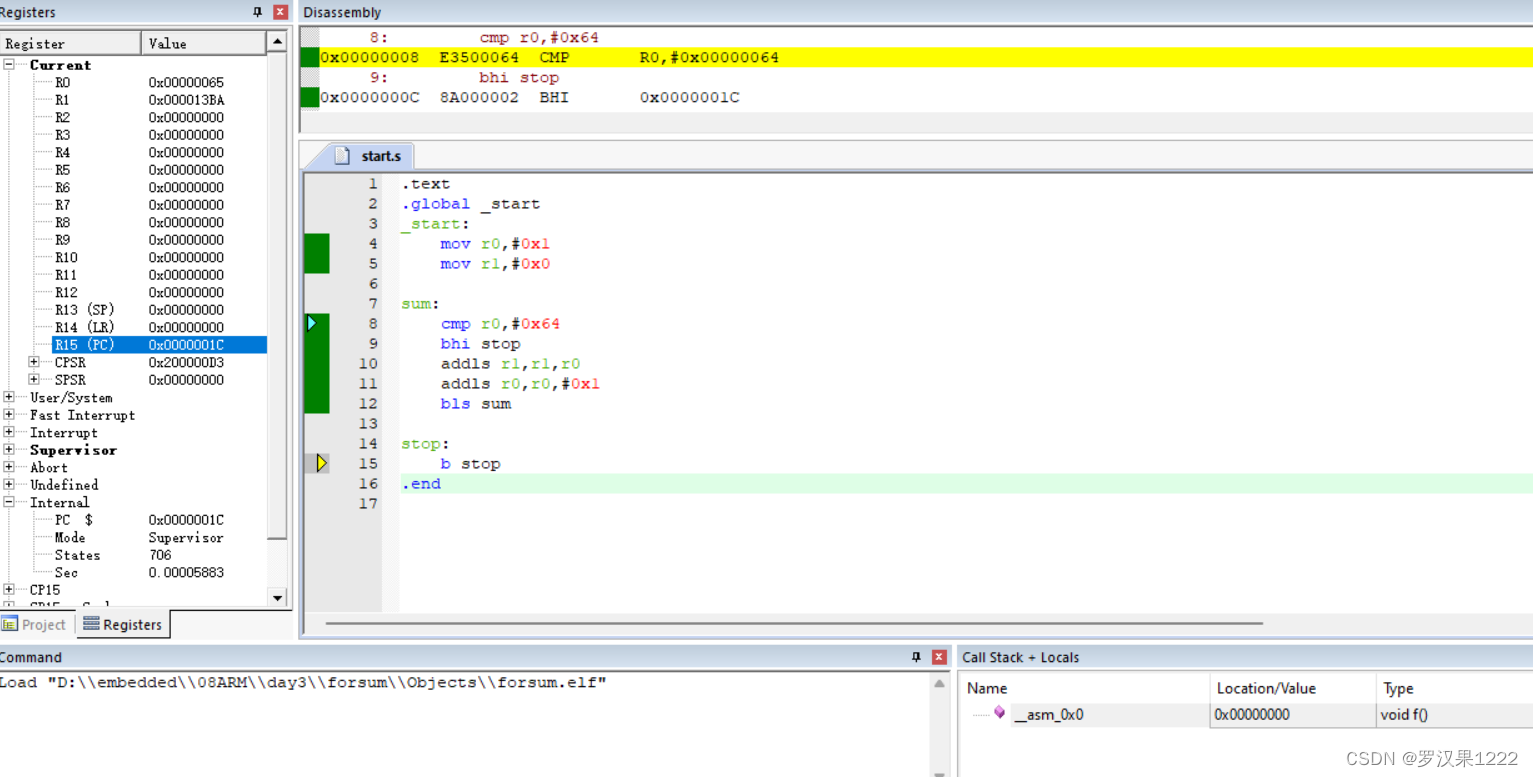
ARMday2
.text .global _start _start:mov r0,#0x1mov r1,#0x0sum:cmp r0,#0x64bhi stopaddls r1,r1,r0addls r0,r0,#0x1bls sumstop:b stop .end...
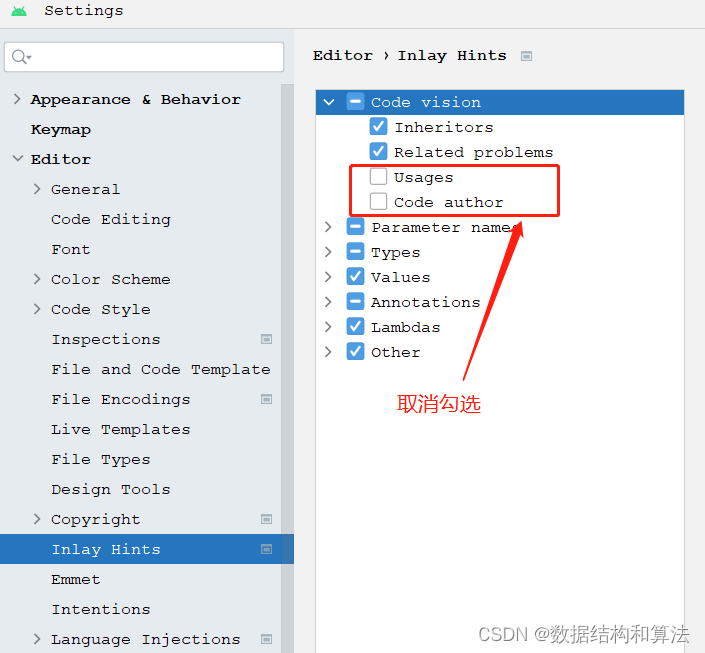
IntelliJ IDEA和Android studio怎么去掉usage和作者提示
截止到目前我已经写了 600多道算法题,其中部分已经整理成了pdf文档,目前总共有1000多页(并且还会不断的增加),大家可以免费下载 下载链接:https://pan.baidu.com/s/1hjwK0ZeRxYGB8lIkbKuQgQ 提取码…...
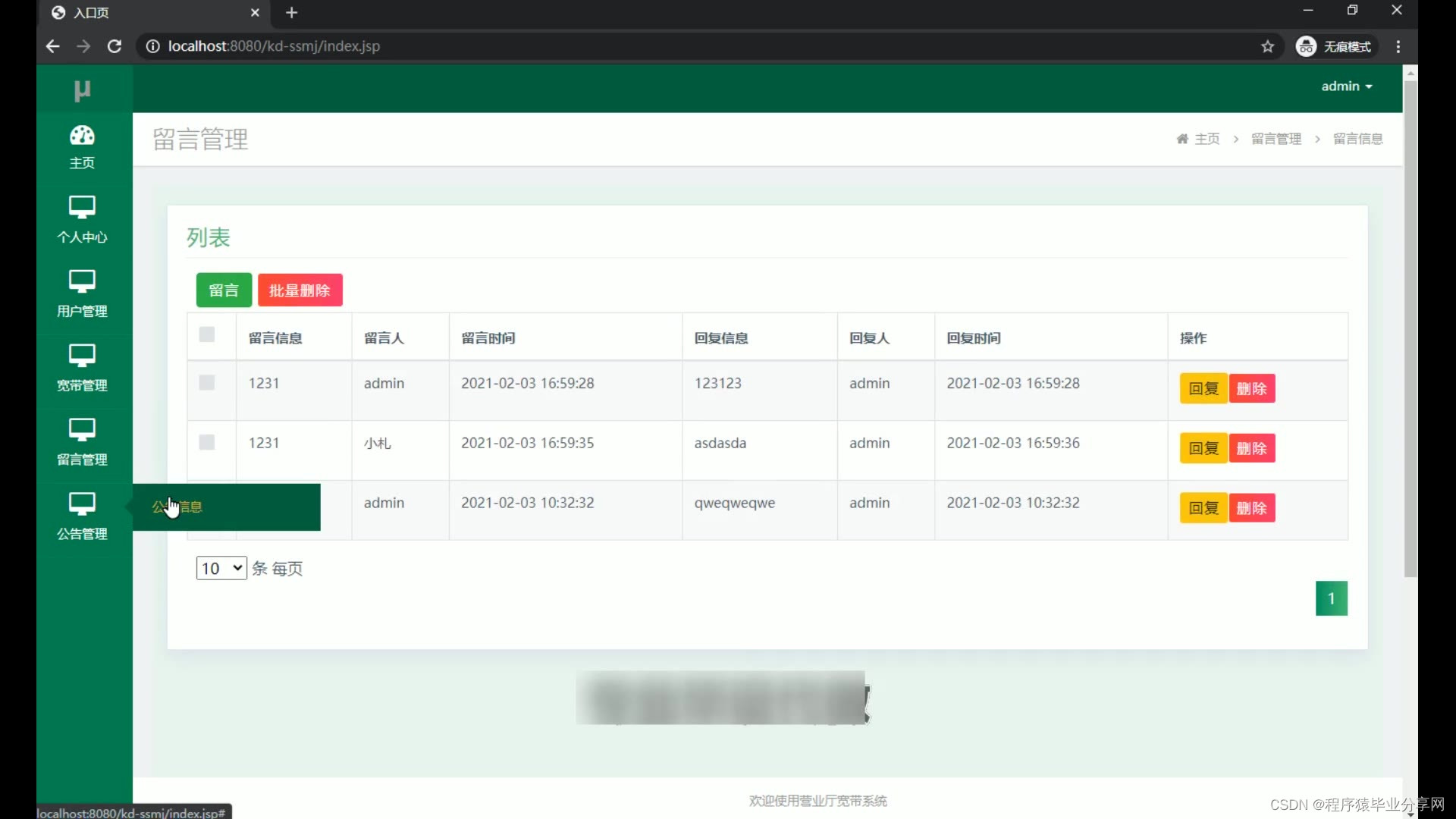
ssm营业厅宽带系统源码和论文
ssm简易版营业厅宽带系统源码和论文018 开发工具:idea 数据库mysql5.7 数据库链接工具:navcat,小海豚等 技术:ssm 摘 要 现代经济快节奏发展以及不断完善升级的信息化技术,让传统数据信息的管理升级为软件存储,…...

CSS:background 复合属性详解(用法 + 例子 + 效果)
目录 background 复合属性background-color 背景颜色(纯)background-image 背景图片 或者 渐变颜色background-repeat 背景是否重复background-size 设置图片大小background-position 设置背景图片显示位置background-attachment 设置背景图片是否随页面…...

django中实现事务/django实现悲观锁乐观锁案例
django中实现事务的几种方式 # 1 全局开启事务---> 全局开启事务,绑定的是http请求响应整个过程DATABASES {default: {#全局开启事务,绑定的是http请求响应整个过程ATOMIC_REQUESTS: True, }}from django.db import transaction# 局部禁用事务trans…...

自动驾驶技术:改变交通出行的未来
自动驾驶技术,这个让人充满期待的技术,正在改变我们的交通方式,带来一种全新的出行体验。它可以让汽车、无人机等交通工具像人类驾驶一样自主行驶,通过人工智能、视觉计算、雷达、监控装置和全球定位系统协同合作,实现…...

5.利用matlab完成 符号矩阵的转置和 符号方阵的幂运算(matlab程序)
1.简述 Matlab符号运算中的矩阵转置 转置向量或矩阵 B A. B transpose(A) 说明 B A. 返回 A 的非共轭转置,即每个元素的行和列索引都会互换。如果 A 包含复数元素,则 A. 不会影响虚部符号。例如,如果 A(3,2) 是 12i 且 B A.࿰…...

为什么要自动化Web测试?
Web自动化是更快地实现所需结果的较佳方式。自动化测试在市场上引起了巨大的轰动。此软件测试过程可以让您使用正确的自动化测试工具和技术集自动执行测试过程。我们执行它是为了检查软件应用程序是否具有完全按照我们希望它执行的方式执行的勇气。 比以往更快地获得反馈 自动化…...

Spark_RDD的容错机制_数据丢失恢复
我们都知道Spark是弹性分布式数据集,数据会存储在多台机器上,那么如何确保在分布式数据计算中,数据不丢失就是其中的关键的部分。本文主要讲解一下Spark中的容错机制。 Spark 主要提供了3个层面的数据容错机制。分别是 调度层,RDD…...

VB+SQL期刊信息管理系统设计与实现
摘 要 本次毕业设计课题为“期刊信息管理系统”,该系统在正常运营中总是面对大量的读者信息、期刊信息以及两者相互作用产生的借刊信息,还刊信息。因此需要对读者资源、期刊资源、借刊信息、还刊信息进行管理,及时了解各个环节中信息的变更,有利于提高管理效率。 此次毕…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

Spring Security 认证流程——补充
一、认证流程概述 Spring Security 的认证流程基于 过滤器链(Filter Chain),核心组件包括 UsernamePasswordAuthenticationFilter、AuthenticationManager、UserDetailsService 等。整个流程可分为以下步骤: 用户提交登录请求拦…...

渗透实战PortSwigger靶场:lab13存储型DOM XSS详解
进来是需要留言的,先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码,输入的<>当成字符串处理回显到页面中,看来只是把用户输…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...
