如何理解“对矩阵进行初等行变换不改变其列向量的线性关系”?
对矩阵A进行初等行变换相当于左乘一个可逆矩阵P。
把A看作是列向量组,若有Ax=0,则其中的x就说明了列向量的线性关系:
[ α 1 , α 2 , α 3 ] [ x 1 x 2 x 3 ] = [ 0 ] \left[ \alpha_1 ,\alpha_2, \alpha_3 \right] \begin{bmatrix} x_1\\ x_2\\ x_3 \end{bmatrix}=\begin{bmatrix} 0\end{bmatrix} [α1,α2,α3] x1x2x3 =[0]
x 1 α 1 + x 2 α 2 + x 3 α 3 = 0 x_1\alpha_1+x_2\alpha_2+x_3\alpha_3=0 x1α1+x2α2+x3α3=0
若对A进行初等行变换后得到了 P A x = 0 PAx=0 PAx=0,知 A x = 0 Ax=0 Ax=0与 P A x = 0 PAx=0 PAx=0同解,就说明了x也适用于矩阵 P A PA PA的列向量之间的线性关系
所以 A A A 与 P A PA PA 的列向量有相同的线性关系。
此外, P A PA PA的行向量组与A的行向量组等价。把A看作是行向量组,若 P A = B PA=B PA=B,有:
[ p 11 p 12 p 13 p 21 p 22 p 23 p 31 p 32 p 33 ] [ α 1 α 2 α 3 ] = [ β 1 β 2 β 3 ] = [ p 11 α 1 + p 12 α 2 + p 13 α 3 p 21 α 1 + p 22 α 2 + p 23 α 3 p 31 α 1 + p 32 α 2 + p 33 α 3 ] \begin{bmatrix} p_{11} & p_{12} & p_{13} \\ p_{21} & p_{22} & p_{23} \\ p_{31} & p_{32} & p_{33} \end{bmatrix}\begin{bmatrix} \alpha_1 \\ \alpha_2 \\ \alpha _3 \end{bmatrix}=\begin{bmatrix} \beta_1 \\ \beta_2 \\ \beta_3 \end{bmatrix} =\begin{bmatrix} p_{11}\alpha _{1}+p_{12}\alpha_2 +p_{13}\alpha _{3} \\ p_{21}\alpha _{1}+p_{22}\alpha_2+p_{23}\alpha_3 \\ p_{31}\alpha _{1}+p_{32}\alpha_2+p_{33}\alpha_3 \end{bmatrix} p11p21p31p12p22p32p13p23p33 α1α2α3 = β1β2β3 = p11α1+p12α2+p13α3p21α1+p22α2+p23α3p31α1+p32α2+p33α3
可知矩阵B的每一个行向量都能用矩阵A的行向量进行线性表出。又由于矩阵P可逆,故 A = P − 1 B A=P^{-1}B A=P−1B,同理可知矩阵A的每一个行向量也可由矩阵B的行向量进行线性表出。
因此矩阵A的行向量组与矩阵B的行向量组等价。
相关文章:

如何理解“对矩阵进行初等行变换不改变其列向量的线性关系”?
对矩阵A进行初等行变换相当于左乘一个可逆矩阵P。 把A看作是列向量组,若有Ax0,则其中的x就说明了列向量的线性关系: [ α 1 , α 2 , α 3 ] [ x 1 x 2 x 3 ] [ 0 ] \left[ \alpha_1 ,\alpha_2, \alpha_3 \right] \begin{bmatrix} x_1\\ x…...
书店行业小程序开发攻略
随着移动互联网的快速发展,小程序成为了各行各业的热门选择,包括书店行业。书店小程序的开发可以为书店提供在线销售渠道,提高销售额,增强用户粘性。本文将介绍如何从搭建到上线开发一款书店行业小程序。 首先,我们需要…...

情感分析工具: TextBlob 与 VADER 的对比
一、说明 在本文我们将看到,在情感分析方面,我们更喜欢哪个库。这取决于很多情况。例如。数据采集。在我们进行分析之前,让我们先看看这两个库是关于什么的。 二、亮相工具库 2.1. 工具库TextBlob介绍: 图像。TextBlob: Simplif…...

uft8和utf8mb4的区别
文章目录 1、Unicode字符集2、UTF-8 编码3、utf8mb3 字符集4、utf8mb4 字符集5、utf8mb3和utf8mb4的区别 1、Unicode字符集 Unicode(统一码、万国码、单一码)是计算机科学领域里的一项业界标准,包括字符集、编码方案等。Unicode 是为了解决传…...

针对低分辨率或小目标的卷积-SPDConv
针对低分辨率或小目标的卷积-SPDConv 摘要引言A New Building Block:SPD-Conv附录代码: 摘要 卷积神经网络在许多计算机视觉任务中取得了巨大成功。然而,在图像低分辨率或目标较小任务上,他们的性能迅速下降。在本文中,我们指出&…...

vue基础-vue监听当前屏幕大小做不同的操作
文章目录 前言一、代码如下:总结 前言 在vue项目开发过程中,有个需求,就是当屏幕大于1024时,我们默认为PC模式。小于1024时,我们默认为H5模式。但是有的界面我们想在PC和H5上面展示不同的数据,请求不同的接…...

Unity框架学习--3
单例模式基类 构造函数私有化,防止外部创建对象 提供一个属性给外部访问,这个属性就相当于是这个类的唯一对象 分为懒汉模式和饿汉模式 不继承MonoBehaviour的单例模式 public static MyUiManager Instance {get{if (instance null){instance new …...
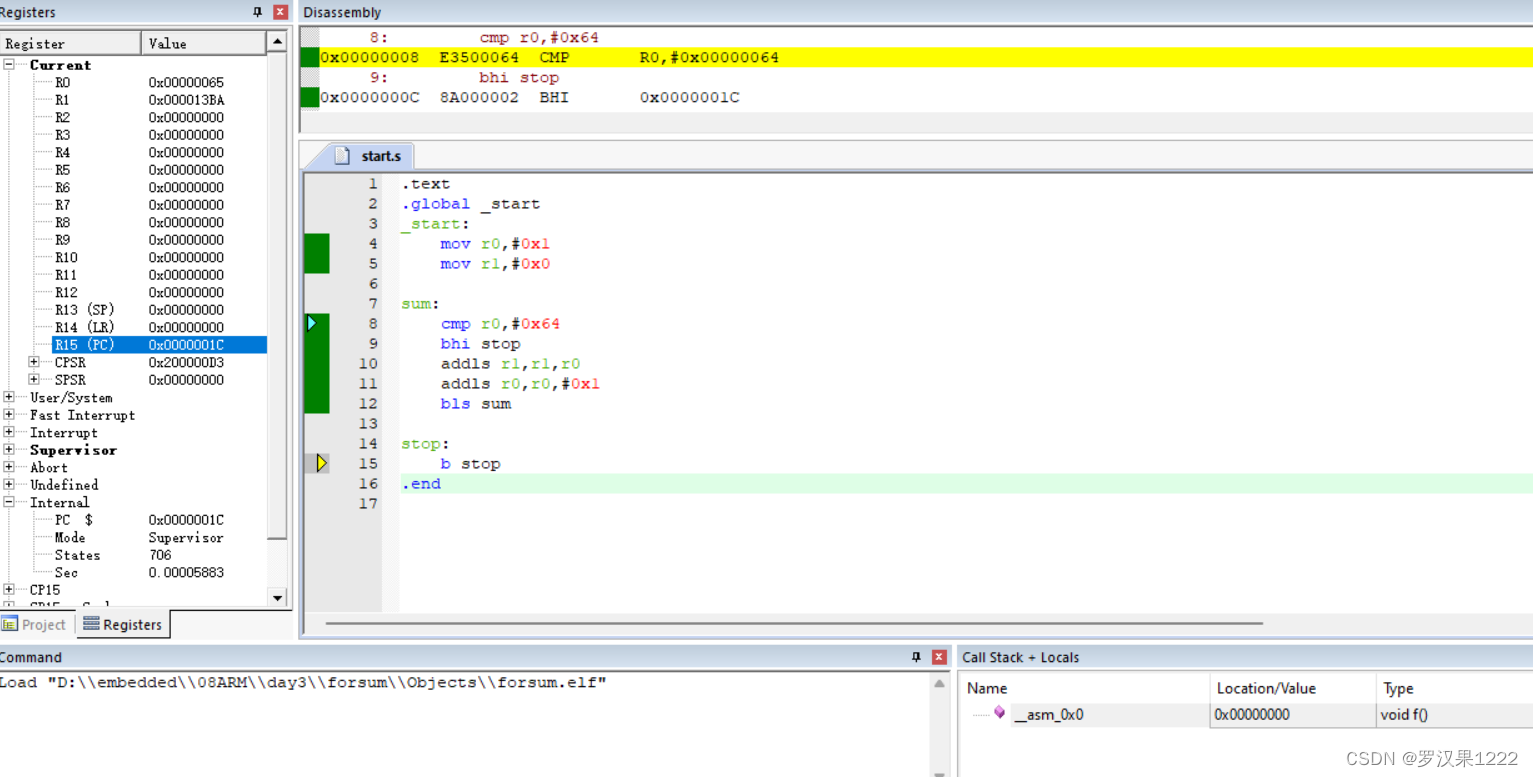
ARMday2
.text .global _start _start:mov r0,#0x1mov r1,#0x0sum:cmp r0,#0x64bhi stopaddls r1,r1,r0addls r0,r0,#0x1bls sumstop:b stop .end...
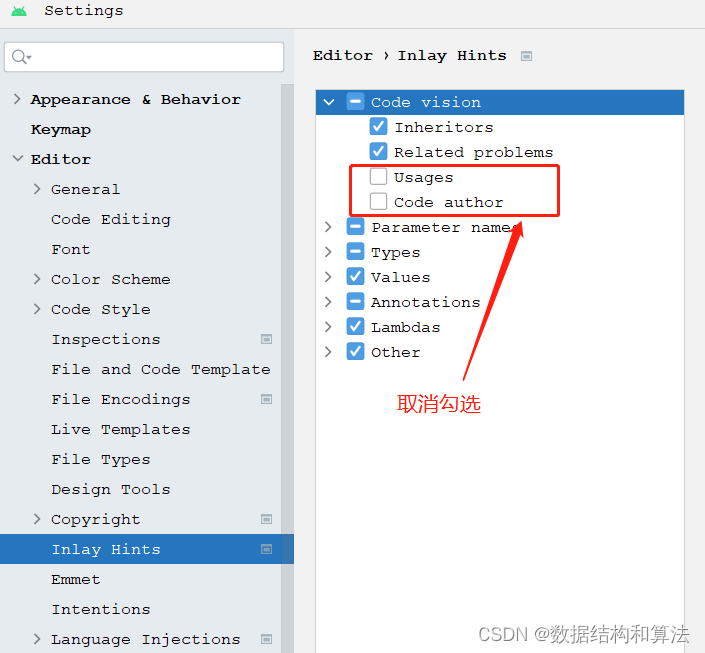
IntelliJ IDEA和Android studio怎么去掉usage和作者提示
截止到目前我已经写了 600多道算法题,其中部分已经整理成了pdf文档,目前总共有1000多页(并且还会不断的增加),大家可以免费下载 下载链接:https://pan.baidu.com/s/1hjwK0ZeRxYGB8lIkbKuQgQ 提取码…...
ssm营业厅宽带系统源码和论文
ssm简易版营业厅宽带系统源码和论文018 开发工具:idea 数据库mysql5.7 数据库链接工具:navcat,小海豚等 技术:ssm 摘 要 现代经济快节奏发展以及不断完善升级的信息化技术,让传统数据信息的管理升级为软件存储,…...

CSS:background 复合属性详解(用法 + 例子 + 效果)
目录 background 复合属性background-color 背景颜色(纯)background-image 背景图片 或者 渐变颜色background-repeat 背景是否重复background-size 设置图片大小background-position 设置背景图片显示位置background-attachment 设置背景图片是否随页面…...

django中实现事务/django实现悲观锁乐观锁案例
django中实现事务的几种方式 # 1 全局开启事务---> 全局开启事务,绑定的是http请求响应整个过程DATABASES {default: {#全局开启事务,绑定的是http请求响应整个过程ATOMIC_REQUESTS: True, }}from django.db import transaction# 局部禁用事务trans…...

自动驾驶技术:改变交通出行的未来
自动驾驶技术,这个让人充满期待的技术,正在改变我们的交通方式,带来一种全新的出行体验。它可以让汽车、无人机等交通工具像人类驾驶一样自主行驶,通过人工智能、视觉计算、雷达、监控装置和全球定位系统协同合作,实现…...

5.利用matlab完成 符号矩阵的转置和 符号方阵的幂运算(matlab程序)
1.简述 Matlab符号运算中的矩阵转置 转置向量或矩阵 B A. B transpose(A) 说明 B A. 返回 A 的非共轭转置,即每个元素的行和列索引都会互换。如果 A 包含复数元素,则 A. 不会影响虚部符号。例如,如果 A(3,2) 是 12i 且 B A.࿰…...

为什么要自动化Web测试?
Web自动化是更快地实现所需结果的较佳方式。自动化测试在市场上引起了巨大的轰动。此软件测试过程可以让您使用正确的自动化测试工具和技术集自动执行测试过程。我们执行它是为了检查软件应用程序是否具有完全按照我们希望它执行的方式执行的勇气。 比以往更快地获得反馈 自动化…...

Spark_RDD的容错机制_数据丢失恢复
我们都知道Spark是弹性分布式数据集,数据会存储在多台机器上,那么如何确保在分布式数据计算中,数据不丢失就是其中的关键的部分。本文主要讲解一下Spark中的容错机制。 Spark 主要提供了3个层面的数据容错机制。分别是 调度层,RDD…...

VB+SQL期刊信息管理系统设计与实现
摘 要 本次毕业设计课题为“期刊信息管理系统”,该系统在正常运营中总是面对大量的读者信息、期刊信息以及两者相互作用产生的借刊信息,还刊信息。因此需要对读者资源、期刊资源、借刊信息、还刊信息进行管理,及时了解各个环节中信息的变更,有利于提高管理效率。 此次毕…...

如何在iPhone手机上修改手机定位和模拟导航?
如何在iPhone手机上修改手机定位和模拟导航? English 首先,你需要在Mac电脑上下载安装 Location Simulator/定位模拟工具 和 Runner 这两款应用程序。 完成安装后,打开软件,并用USB连接手机设备 修改iPhone手机定位和模拟导航 …...

Linux 当fork在for循环中的问题
以下代码会打印几个"A"? 例1.代码如下: int main(int argc, char* argv[],char* envp[]) { for(int i 0;i < 2; i ) { fork(); printf("A\n"); } exit(0); } 代码分析: //父进程for(int i …...
推断统计中非参数检验之卡方检验、列联表分析和游程检验
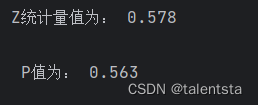
一、(卡方检验):赛马比赛的赛道会影响成绩吗 这里以一个实例赛马比赛的赛道是否会影响成绩为例,实际就是检验获胜频数与期望频数之间有无显著性差异。 import pandas as pdstep1 调用包 from scipy.stats import chisquare impor…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

算法打卡第18天
从中序与后序遍历序列构造二叉树 (力扣106题) 给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。 示例 1: 输入:inorder [9,3,15,20,7…...

WEB3全栈开发——面试专业技能点P4数据库
一、mysql2 原生驱动及其连接机制 概念介绍 mysql2 是 Node.js 环境中广泛使用的 MySQL 客户端库,基于 mysql 库改进而来,具有更好的性能、Promise 支持、流式查询、二进制数据处理能力等。 主要特点: 支持 Promise / async-await…...
