【数理知识】三维空间旋转矩阵的欧拉角表示法,四元数表示法,两者之间的转换,Matlab 代码实现
| 序号 | 内容 |
|---|---|
| 1 | 【数理知识】自由度 degree of freedom 及自由度的计算方法 |
| 2 | 【数理知识】刚体 rigid body 及刚体的运动 |
| 3 | 【数理知识】刚体基本运动,平动,转动 |
| 4 | 【数理知识】向量数乘,内积,外积,matlab代码实现 |
| 5 | 【数理知识】最小二乘法,从线性回归出发,数值举例并用最小二乘法求解回归模型 |
| 6 | 【数理知识】最小二乘法,一般线性情况,矩阵化表示过程,最佳参数的求解公式过程 |
| 7 | 【数理知识】协方差,随机变量的的协方差,随机变量分别是单个数字和向量时的协方差 |
| 8 | 【数理知识】奇异值分解,从数据的线性变换角度来理解 |
| 9 | 【数理知识】旋转矩阵的推导过程,基于向量的旋转来实现,同时解决欧式变换的非线性局限 |
| 10 | 【数理知识】三维空间旋转矩阵的欧拉角表示法,四元数表示法,两者之间的转换,Matlab 代码实现 |
| 11 | 【数理知识】已知 N>=3 个点在前后时刻的坐标,求刚体平移矩阵,旋转矩阵,且这 N>=3 点间距离始终不变代表一个刚体 |
文章目录
- 1. 欧拉角(Euler Angles)表示法
- 2. 四元数(Quaternion)表示法
- 3. 四元数转欧拉角
- 4. 欧拉角转四元数
- Ref
之前我们已经讨论过旋转矩阵。需要再次强调的是,旋转的顺序很重要,并且会影响最终的结果。先旋转 X X X 轴,再旋转 Y Y Y 轴,最后旋转 Z Z Z 轴得到的结果与先旋转 Z Z Z 轴,再旋转 Y Y Y 轴,最后旋转 X X X 轴得到的结果是不同的。这种顺序的差异导致了不同的方向和空间方向的变化。这也是为什么在实际应用中,我们需要明确指定旋转顺序,以确保我们得到正确和一致的结果。
这次基于三维空间,讨论下旋转矩阵的两种表示方法,分别是欧拉角表示法,四元数表示法,以及二者之间的转换关系如何。
在三维空间中,旋转矩阵 R R R 的维度为 3 × 3 3 \times 3 3×3,其是一个正交矩阵,行列式为 1 1 1。
1. 欧拉角(Euler Angles)表示法
欧拉角通常由三个角度组成
- 滚转角(roll),常用符号为 ϕ \phi ϕ
- 俯仰角(pitch),常用符号为 θ \theta θ
- 偏航角(yaw),常用符号为 ψ \psi ψ
这三个角度分别描述了绕 X , Y , Z X, Y, Z X,Y,Z 轴旋转的角度。
绕 X X X 轴旋转 ϕ \phi ϕ 角度的旋转矩阵为
R x ( ϕ ) = [ 1 0 0 0 cos ( ϕ ) − sin ( ϕ ) 0 sin ( ϕ ) cos ( ϕ ) ] R_x(\phi) = \left[\begin{matrix} 1 & 0 & 0 \\ 0 & \cos(\phi) & -\sin(\phi) \\ 0 & \sin(\phi) & \cos(\phi) \\ \end{matrix}\right] Rx(ϕ)= 1000cos(ϕ)sin(ϕ)0−sin(ϕ)cos(ϕ)
绕 Y Y Y 轴旋转 θ \theta θ 角度的旋转矩阵为
R y ( θ ) = [ cos ( θ ) 0 sin ( θ ) 0 1 0 − sin ( θ ) 0 cos ( θ ) ] R_y(\theta) = \left[\begin{matrix} \cos(\theta) & 0 & \sin(\theta) \\ 0 & 1 & 0 \\ -\sin(\theta) & 0 & \cos(\theta) \\ \end{matrix}\right] Ry(θ)= cos(θ)0−sin(θ)010sin(θ)0cos(θ)
绕 Z Z Z 轴旋转 ψ \psi ψ 角度的旋转矩阵为
R z ( ψ ) = [ cos ( ψ ) − sin ( ψ ) 0 sin ( ψ ) cos ( ψ ) 0 0 0 1 ] R_z(\psi) = \left[\begin{matrix} \cos(\psi) & -\sin(\psi) & 0 \\ \sin(\psi) & \cos(\psi) & 0 \\ 0 & 0 & 1 \\ \end{matrix}\right] Rz(ψ)= cos(ψ)sin(ψ)0−sin(ψ)cos(ψ)0001
例如,对于一个分别依次绕固定轴 X Y Z XYZ XYZ 的欧拉角表示,其旋转矩阵为
R = R z ( ϕ ) R y ( θ ) R x ( ψ ) = [ cos ( θ ) cos ( ψ ) sin ( ϕ ) sin ( θ ) cos ( ψ ) − cos ( ϕ ) sin ( ψ ) cos ( ϕ ) sin ( θ ) cos ( ψ ) + sin ( ϕ ) sin ( ψ ) cos ( θ ) sin ( ψ ) sin ( ϕ ) sin ( θ ) sin ( ψ ) + cos ( ϕ ) cos ( ψ ) cos ( ϕ ) sin ( θ ) sin ( ψ ) − sin ( ϕ ) cos ( ψ ) − sin ( θ ) sin ( ϕ ) cos ( θ ) cos ( ϕ ) cos ( θ ) ] \begin{aligned} R &= R_z(\phi) R_y(\theta) R_x(\psi) \\ &= \left[\begin{matrix} \cos(\theta)\cos(\psi) & \sin(\phi)\sin(\theta)\cos(\psi) - \cos(\phi)\sin(\psi) & \cos(\phi)\sin(\theta)\cos(\psi) + \sin(\phi)\sin(\psi) \\ \cos(\theta)\sin(\psi) & \sin(\phi)\sin(\theta)\sin(\psi) + \cos(\phi)\cos(\psi) & \cos(\phi)\sin(\theta)\sin(\psi) - \sin(\phi)\cos(\psi) \\ -\sin(\theta) & \sin(\phi)\cos(\theta) & \cos(\phi)\cos(\theta) \\ \end{matrix}\right] \end{aligned} R=Rz(ϕ)Ry(θ)Rx(ψ)= cos(θ)cos(ψ)cos(θ)sin(ψ)−sin(θ)sin(ϕ)sin(θ)cos(ψ)−cos(ϕ)sin(ψ)sin(ϕ)sin(θ)sin(ψ)+cos(ϕ)cos(ψ)sin(ϕ)cos(θ)cos(ϕ)sin(θ)cos(ψ)+sin(ϕ)sin(ψ)cos(ϕ)sin(θ)sin(ψ)−sin(ϕ)cos(ψ)cos(ϕ)cos(θ)
这个矩阵代表了首先绕 X X X 轴旋转 ϕ \phi ϕ 角,然后绕 Y Y Y 轴旋转 θ \theta θ 角,再然后绕 Z Z Z 轴旋转 ψ \psi ψ 角的总的旋转效果。
更多关于欧拉角的推导和细节可参考文章:第3章-数理知识基础 -> 坐标转换和【数理知识】旋转矩阵的推导过程,基于向量的旋转来实现,同时解决欧式变换的非线性局限。
% 给定欧拉角 phi theta psi
phi = deg2rad(10); % 示例:10度,记得转换为弧度
theta = deg2rad(22); % 示例:22度
psi = deg2rad(35); % 示例:35度R_x = [ 1 0 00 cos(phi) -sin(phi)0 sin(phi) cos(phi)];R_y = [ cos(theta) 0 sin(theta)0 1 0-sin(theta) 0 cos(theta)];R_z = [ cos(psi) -sin(psi) 0sin(psi) cos(psi) 00 0 1];R = R_z * R_y * R_x;R = [cos(theta)*cos(psi) sin(phi)*sin(theta)*cos(psi)-cos(phi)*sin(psi) cos(phi)*sin(theta)*cos(psi)+sin(phi)*sin(psi)cos(theta)*sin(psi) sin(phi)*sin(theta)*sin(psi)+cos(phi)*cos(psi) cos(phi)*sin(theta)*sin(psi)-sin(phi)*cos(psi)-sin(theta) sin(phi)*cos(theta) cos(phi)*cos(theta)];
R =0.7595 -0.5116 0.40180.5318 0.8440 0.0694-0.3746 0.1610 0.9131
% 给定点坐标
point_1 = [ 102235];
point_2 = R * point_1;figure()
scatter3(point_1(1), point_1(2), point_1(3), 150, 'r'); hold on;
scatter3(point_2(1), point_2(2), point_2(3), 150, 'b');

2. 四元数(Quaternion)表示法
四元数是由 1 1 1 个实数加上 3 3 3 个复数组合而成,通常可以表示为
q = q w + q x i + q y j + q z k q = q_w + q_x \text{i} + q_y \text{j} + q_z \text{k} q=qw+qxi+qyj+qzk
其中 q w , q x , q y , q z q_w, q_x, q_y, q_z qw,qx,qy,qz 都是实数, i, j, k \text{i, j, k} i, j, k 是四元数的基元,满足如下所示的乘法关系
- i 2 = j 2 = k 2 = ijk = − 1 \text{i}^2 = \text{j}^2 = \text{k}^2 = \text{i}\text{j}\text{k} = -1 i2=j2=k2=ijk=−1
- i 0 = j 0 = k 0 = 1 \text{i}^0 = \text{j}^0 = \text{k}^0 = 1 i0=j0=k0=1
四元数还可看作由一个标量和一个向量组成,其中 q w q_w qw 是四元数的标量部分, q x , q y , q z q_x, q_y, q_z qx,qy,qz 构成四元数的向量部分。
假设有两个四元数分别为 q 1 = ( q w 1 , [ q x 1 , q y 1 , q z 1 ] ) q_1 = (q_{w1}, [q_{x1}, q_{y1}, q_{z1}]) q1=(qw1,[qx1,qy1,qz1]), q 2 = ( q w 2 , [ q x 2 , q y 2 , q z 2 ] ) q_2 = (q_{w2}, [q_{x2}, q_{y2}, q_{z2}]) q2=(qw2,[qx2,qy2,qz2]),同时令 v 1 = [ q x 1 , q y 1 , q z 1 ] v_1 = [q_{x1}, q_{y1}, q_{z1}] v1=[qx1,qy1,qz1], v 2 = [ q x 2 , q y 2 , q z 2 ] v_2 = [q_{x2}, q_{y2}, q_{z2}] v2=[qx2,qy2,qz2],则有如下运算法则
- 四元数的和: q 1 + q 2 = ( q w 1 + q w 2 , ( v 1 + v 2 ) ) q_1 + q_2 = (q_{w1}+q_{w2}, (v_1 +v_2)) q1+q2=(qw1+qw2,(v1+v2))
- 四元数乘法: q 1 q 2 = q w 1 q w 2 − v 1 ⋅ v 2 + q w 1 v 2 + q w 2 v 1 + v 1 × v 2 = ( q w 1 q w 2 − v 1 ⋅ v 2 , ( q w 1 v 2 + q w 2 v 1 + v 1 × v 2 ) ) q_1 q_2 = q_{w1} q_{w2} - v_1 \cdot v_2 + q_{w1} v_2 + q_{w2} v_1 + v_1 \times v_2 = (q_{w1} q_{w2} - v_1 \cdot v_2, (q_{w1} v_2 + q_{w2} v_1 + v_1 \times v_2)) q1q2=qw1qw2−v1⋅v2+qw1v2+qw2v1+v1×v2=(qw1qw2−v1⋅v2,(qw1v2+qw2v1+v1×v2))
- 四元数的模: ∥ q 1 ∥ = q w 1 2 + q x 1 2 + q y 1 2 + q z 1 2 \|q_1\| = \sqrt{q_{w1}^2 + q_{x1}^2 + q_{y1}^2 + q_{z1}^2} ∥q1∥=qw12+qx12+qy12+qz12
- 单位四元数: ∥ q 1 ∥ = 1 \|q_1\| = 1 ∥q1∥=1
- 四元数的共轭: q 1 ∗ = ( q w 1 , − v 1 ) q_1^* = (q_{w1}, -v_1) q1∗=(qw1,−v1)
- 四元数的逆: q 1 − 1 = q 1 ∗ ∥ q 1 ∥ q_1^{-1} = \frac{q_1^*}{\|q_1\|} q1−1=∥q1∥q1∗
四元数是一个扩展的复数系统,常用于表示三维空间中的旋转。
一个单位四元数(长度为 1 1 1)可以表示 3D 空间中的旋转。将一个点旋转到另一个位置可以通过四元数乘法来完成。
绕 X X X 轴旋转 ϕ \phi ϕ 角度的四元数为
q ϕ = ( cos ( ϕ 2 ) , sin ( ϕ 2 ) , 0 , 0 ) q_\phi = (\cos(\frac{\phi}{2}), \sin(\frac{\phi}{2}), 0, 0) qϕ=(cos(2ϕ),sin(2ϕ),0,0)
绕 Y Y Y 轴旋转 θ \theta θ 角度的四元数为
q θ = ( cos ( θ 2 ) , 0 , sin ( θ 2 ) , 0 , 0 ) q_\theta = (\cos(\frac{\theta}{2}), 0, \sin(\frac{\theta}{2}), 0, 0) qθ=(cos(2θ),0,sin(2θ),0,0)
绕 Z Z Z 轴旋转 ψ \psi ψ 角度的四元数为
q ψ = ( cos ( ψ 2 ) , 0 , 0 , sin ( ψ 2 ) ) q_\psi = (\cos(\frac{\psi}{2}), 0, 0, \sin(\frac{\psi}{2})) qψ=(cos(2ψ),0,0,sin(2ψ))
总旋转的四元数是这三个四元数的乘积。四元数乘法不是通常的标量乘法,它有特定的乘法规则。
给定一个四元数 q q q(模长为 1,有关系 q w 2 + q x 2 + q y 2 + q z 2 = 1 \sqrt{q_w^2+q_x^2+q_y^2+q_z^2}=1 qw2+qx2+qy2+qz2=1),假设采用的旋转顺序为 X Y Z XYZ XYZ,其对应的旋转矩阵 R R R 可以表示为
R = [ 1 − 2 ( q y 2 + q z 2 ) 2 ( q x q y − q w q z ) 2 ( q x q z + q w q y ) 2 ( q x q y + q w q z ) 1 − 2 ( q x 2 + q z 2 ) 2 ( q y q z − q w q x ) 2 ( q x q z − q w q y ) 2 ( q y q z + q w q x ) 1 − 2 ( q x 2 + q y 2 ) ] \begin{aligned} R &= \left[\begin{matrix} 1 - 2(q_y^2 + q_z^2) & 2(q_x q_y - q_w q_z) & 2(q_x q_z + q_w q_y) \\ 2(q_x q_y + q_w q_z) & 1 - 2(q_x^2 + q_z^2) & 2(q_y q_z - q_w q_x) \\ 2(q_x q_z - q_w q_y) & 2(q_y q_z + q_w q_x) & 1 - 2(q_x^2 + q_y^2) \\ \end{matrix}\right] \end{aligned} R= 1−2(qy2+qz2)2(qxqy+qwqz)2(qxqz−qwqy)2(qxqy−qwqz)1−2(qx2+qz2)2(qyqz+qwqx)2(qxqz+qwqy)2(qyqz−qwqx)1−2(qx2+qy2)
单位四元数在描述 3D 旋转时有一些优势,其不受欧拉角中的 “万向锁” 问题的影响。
% 给定四元数
quaternion = [0.9376 0.0244 0.2070 0.2782]; q_w = quaternion(1);
q_x = quaternion(2);
q_y = quaternion(3);
q_z = quaternion(4);% 计算旋转矩阵 R
R(1,1) = 1 - 2*(q_y^2 + q_z^2);
R(1,2) = 2*(q_x*q_y - q_w*q_z);
R(1,3) = 2*(q_x*q_z + q_w*q_y);
R(2,1) = 2*(q_x*q_y + q_w*q_z);
R(2,2) = 1 - 2*(q_x^2 + q_z^2);
R(2,3) = 2*(q_y*q_z - q_w*q_x);
R(3,1) = 2*(q_x*q_z - q_w*q_y);
R(3,2) = 2*(q_y*q_z + q_w*q_x);
R(3,3) = 1 - 2*(q_x^2 + q_y^2);
R =0.7595 -0.5116 0.40170.5318 0.8440 0.0694-0.3746 0.1609 0.9131
3. 四元数转欧拉角
从四元数到欧拉角的转换并不是唯一的,因为对于某些旋转,存在多种欧拉角表示。但是,对于大多数实际应用,可以从一个特定的四元数计算一个特定的欧拉角集。
给定四元数 q = ( q w , q x , q y , q z ) q = (q_w, q_x, q_y, q_z) q=(qw,qx,qy,qz),若想将它转换为 X Y Z XYZ XYZ 顺序的欧拉角 ( ϕ , θ , ψ ) (\phi, \theta, \psi) (ϕ,θ,ψ)。以下是从四元数到欧拉角的转换方法
ϕ = atan2 ( 2 ( q w q x + q y q z ) , 1 − 2 ( q x 2 + q y 2 ) ) θ = arcsin ( 2 ( q w q y − q x q z ) ) ψ = atan2 ( 2 ( q w q z + q x q y ) , 1 − 2 ( q y 2 + q z 2 ) ) \begin{aligned} \phi &= \text{atan2} (2(q_w q_x + q_y q_z), 1-2(q_x^2 + q_y^2)) \\ \theta &= \text{} \arcsin (2(q_w q_y - q_x q_z)) \\ \psi&= \text{atan2} (2(q_w q_z + q_x q_y), 1-2(q_y^2 + q_z^2)) \end{aligned} ϕθψ=atan2(2(qwqx+qyqz),1−2(qx2+qy2))=arcsin(2(qwqy−qxqz))=atan2(2(qwqz+qxqy),1−2(qy2+qz2))
其中 atan2 ( ) \text{atan2}() atan2() 不是 arctan ( ) \arctan() arctan()。
举例说明,因为若使用 arctan ( y / x ) \arctan(y/x) arctan(y/x),其返回值在 [ − π / 2 , π / 2 ] [-\pi/2, \pi/2] [−π/2,π/2] 之间,因为它不能区分 x x x 的正负。而 atan2 ( y , x ) \text{atan2}(y, x) atan2(y,x),其返回值在 [ − π , π ] [-\pi, \pi] [−π,π] 之间,可以区分 x x x 的正负,因此更为实用,尤其是在计算欧拉角时。更重要的是, atan2 ( y , x ) \text{atan2}(y, x) atan2(y,x) 能够处理 x = 0 x=0 x=0 的情况,这在计算角度或欧拉角时非常有用。
注意,由于使用 arcsin ( ) \arcsin() arcsin(),当 θ \theta θ 接近 ± 90 ° \pm 90\degree ±90° 时,可能会出现数值不稳定。这是因为在这些极端情况下,航向和滚动变得不可区分,这就是所谓的万向锁问题。
% 给定四元数
quaternion = [0.9376 0.0244 0.2070 0.2782]; q_w = quaternion(1);
q_x = quaternion(2);
q_y = quaternion(3);
q_z = quaternion(4);% 转换四元数到欧拉角
phi = atan2(2*(q_w*q_x + q_y*q_z), 1 - 2*(q_x^2 + q_y^2));
theta = asin(2*(q_w*q_y - q_z*q_x));
psi = atan2(2*(q_w*q_z + q_x*q_y), 1 - 2*(q_y^2 + q_z^2));% 如果需要角度形式而不是弧度,可以转换为度
phi_deg = rad2deg(phi);
theta_deg = rad2deg(theta);
psi_deg = rad2deg(psi);
phi_deg =9.9953theta_deg =21.9990psi_deg =34.9983
4. 欧拉角转四元数
给定三个欧拉角 ϕ , θ , ψ \phi, \theta, \psi ϕ,θ,ψ,相应的四元数为
q w = cos ( ϕ 2 ) cos ( θ 2 ) cos ( ψ 2 ) + sin ( ϕ 2 ) sin ( θ 2 ) sin ( ψ 2 ) q x = sin ( ϕ 2 ) cos ( θ 2 ) cos ( ψ 2 ) − cos ( ϕ 2 ) sin ( θ 2 ) sin ( ψ 2 ) q y = cos ( ϕ 2 ) sin ( θ 2 ) cos ( ψ 2 ) + sin ( ϕ 2 ) cos ( θ 2 ) sin ( ψ 2 ) q z = cos ( ϕ 2 ) cos ( θ 2 ) sin ( ψ 2 ) − sin ( ϕ 2 ) sin ( θ 2 ) cos ( ψ 2 ) \begin{aligned} q_w &= \cos(\frac{\phi}{2}) \cos(\frac{\theta}{2}) \cos(\frac{\psi}{2}) + \sin(\frac{\phi}{2}) \sin(\frac{\theta}{2}) \sin(\frac{\psi}{2}) \\ q_x &= \sin(\frac{\phi}{2}) \cos(\frac{\theta}{2}) \cos(\frac{\psi}{2}) - \cos(\frac{\phi}{2}) \sin(\frac{\theta}{2}) \sin(\frac{\psi}{2}) \\ q_y &= \cos(\frac{\phi}{2}) \sin(\frac{\theta}{2}) \cos(\frac{\psi}{2}) + \sin(\frac{\phi}{2}) \cos(\frac{\theta}{2}) \sin(\frac{\psi}{2}) \\ q_z &= \cos(\frac{\phi}{2}) \cos(\frac{\theta}{2}) \sin(\frac{\psi}{2}) - \sin(\frac{\phi}{2}) \sin(\frac{\theta}{2}) \cos(\frac{\psi}{2}) \end{aligned} qwqxqyqz=cos(2ϕ)cos(2θ)cos(2ψ)+sin(2ϕ)sin(2θ)sin(2ψ)=sin(2ϕ)cos(2θ)cos(2ψ)−cos(2ϕ)sin(2θ)sin(2ψ)=cos(2ϕ)sin(2θ)cos(2ψ)+sin(2ϕ)cos(2θ)sin(2ψ)=cos(2ϕ)cos(2θ)sin(2ψ)−sin(2ϕ)sin(2θ)cos(2ψ)
得到的四元数是 ( q w , q x , q y , q z ) (q_w, q_x, q_y, q_z) (qw,qx,qy,qz)。
phi = deg2rad(10); % 示例:10度,记得转换为弧度
theta = deg2rad(22); % 示例:22度
psi = deg2rad(35); % 示例:35度% 计算四元数
q_w = cos(phi/2) * cos(theta/2) * cos(psi/2) + sin(phi/2) * sin(theta/2) * sin(psi/2);
q_x = sin(phi/2) * cos(theta/2) * cos(psi/2) - cos(phi/2) * sin(theta/2) * sin(psi/2);
q_y = cos(phi/2) * sin(theta/2) * cos(psi/2) + sin(phi/2) * cos(theta/2) * sin(psi/2);
q_z = cos(phi/2) * cos(theta/2) * sin(psi/2) - sin(phi/2) * sin(theta/2) * cos(psi/2);quaternion = [q_w, q_x, q_y, q_z];
quaternion =0.9376 0.0244 0.2070 0.2782
Ref
- 旋转矩阵 - Wikipedia
- 干货整理:欧拉角、旋转矩阵、四元数合辑
相关文章:

【数理知识】三维空间旋转矩阵的欧拉角表示法,四元数表示法,两者之间的转换,Matlab 代码实现
序号内容1【数理知识】自由度 degree of freedom 及自由度的计算方法2【数理知识】刚体 rigid body 及刚体的运动3【数理知识】刚体基本运动,平动,转动4【数理知识】向量数乘,内积,外积,matlab代码实现5【数理知识】最…...

【业务功能篇63】Springboot聊聊 过滤器和拦截器
过滤器的场景:过滤器通常用于对数据或资源进行筛选、修改或转换的场景。例如,在一个电子商务网站中,用户进行商品搜索时,你可以使用过滤器来过滤特定的商品类别、价格范围或其他条件,以便用户仅看到符合筛选条件的结果…...
提高学生学习效率的模拟考试系统
在如今竞争激烈的社会环境下,提高学生的学习效率显得尤为重要。为了帮助学生评估自己的学习水平并提供有针对性的学习建议,开发一款模拟考试系统是非常必要的。 一、学生信息录入 模拟考试系统首先需要学生信息录入功能。学生可以通过一个简单的表单填…...

解决QWebEngineView在linux下加载本地html失败的问题
通常我们使用QWebEngineView加载本地html文件时,是通过 void load(const QUrl &url) void setUrl(const QUrl &url) 两个函数,传入html的相对或绝对路径,进行加载。 而在linux(uos x86)下运行时,却发现加载失败…...

如何使用Redis实现内容推送功能
导读 在日常使用中,我们经常能看见内容推送功能。 常见的场景有,比如你在bilibili关注了某个up主,当up主发布视频后,就会推送到你的收件箱或者是动态中,让粉丝能够及时得知所关注的人发布了内容。 又比如朋友圈&…...
怎么对视频进行压缩?
怎么对视频进行压缩?视频压缩,我们都知道是将视频文件进行压缩变小的过程,是我们日常办公中较为常用的手段。现如今,在视频技术不断发展与创新的基础上,视频分辨率也在不断提高,进而导致文件占有量也非常大…...

redisson配置类---SpringBoot集成、redis单机和集群模式配置
1项目配置文件: 1.1:pom.xml <dependency><groupId>org.redisson</groupId><artifactId>redisson-spring-boot-starter</artifactId><version>3.17.7</version></dependency> 1.2 application.yml配置…...
瓴羊发布All in One 产品,零售SaaS的尽头是DaaS?
“打破烟囱、化繁为简,让丰富的能力、数据和智能All in One”,这是瓴羊新发布的产品瓴羊One承担的使命,也意味着瓴羊DaaS事业迈入了一个新阶段。 成立伊始,瓴羊就打出了“Not SaaS,But DaaS”旗号,将自己的…...
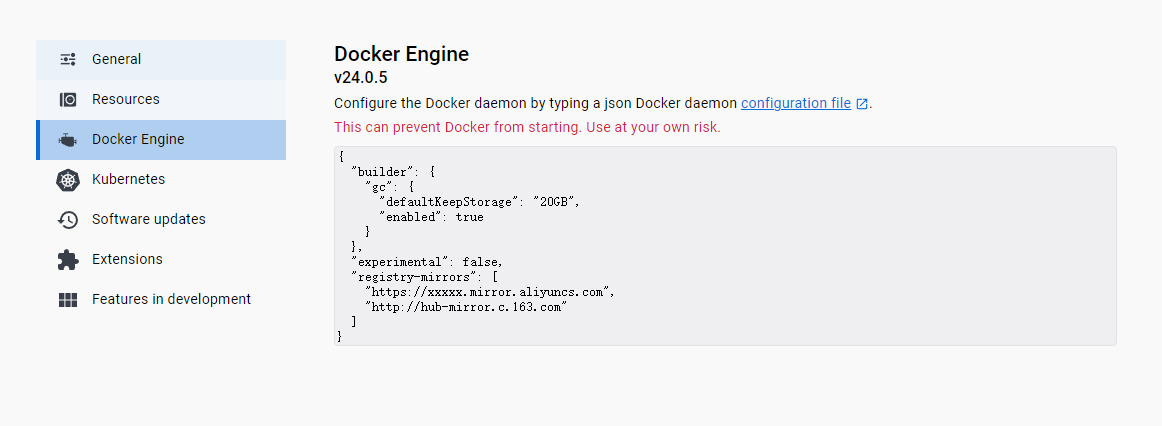
win10中Docker安装、构建镜像、创建容器、Vscode连接实例
Docker方便一键构建项目所需的运行环境:首先构建镜像(Image)。然后镜像实例化成为容器(Container),构成项目的运行环境。最后Vscode连接容器,方便我们在本地进行开发。下面以一个简单的例子介绍在win10中实现:Docker安装、构建镜像…...

贝锐蒲公英:快速搭建连锁门店监控体系,赋能企业高效管理
随着国民生活水平的提高和零售场景的变革,消费者对于餐饮类目的消费支出不断增加,线下社区生鲜商超作为下沉市场最主要的消费场景之一,蕴藏着巨大价值机会。 对于线下连锁生鲜超市而言,连锁门店多、员工多,门店管理时会…...

c++ WinInet InternetOpenUrl下载中文文件
windows自带的WinInet,几个函数就可以实现http文件下载, 且可获取文件大小,进度条等。 在用WinInet下载文件时,遇到个问题, 如果是中文,下载下来的文件大小为0 英文文件正常,为什么呢? bool WWWFileBuffer(const char* host, const char* path, char* outBuffer, in…...
算法通过村第三关-数组青铜笔记|单调数组
文章目录 前言单调数组问题搜索插入位置:数组合并问题:总结 前言 提示:本份真诚面对自己、坦然无碍面对他人,就是优雅。 数组中的比较经典性问题: 单调数组问题数组合并问题 单调数组问题 参考例子:896. 单调数列…...
Springboot MultipartFile文件上传与下载
yml文件配置是否可以上传及上传附件大小 servlet:multipart:# 允许文件上传enabled: true# 单个文件大小max-file-size: 20MB# 设置总上传的文件大小max-request-size: 50MB /*** param files* param request* Description 上传文件* Throws* Return java.util.List* Date 202…...

js this变量
js this变量 有个比较特殊的箭头函数没有自己的this,而是继承了外部作用域的this...

Ubuntu ip冲突,修改静态IP方法
虚拟机克隆Ubuntu造成的IP地址相同冲突的问题_虚拟机ip冲突怎么解决_昌哥不爱晚睡的博客-CSDN博客...

windows下dll文件的创建详细教程
1、前言 dll文件是啥,就不作过多赘述了。现在直接教大家如何创建与使用dll文件。 本文基于windows系统,使用的编译相关工具为visual studio 2019。 2、创建dll 2.1 创建dll工程 首先打开visual studio,然后选择创建新项目,在搜…...

一些Git Repo
文章目录 Fake-TcpWow Fishing Script模拟券商柜台 Fake-Tcp Fake-Tcp 自己写的一个伪装包测试。 尝试把UDP的包伪装成TCP包,再发送到Internet Wow Fishing Script 魔兽世界钓鱼脚本 自己写的魔兽世界钓鱼脚本,10.0初期钓鱼成功率90%以上。现在关服了…...

【Unity脚本开源】记录鼠标按下的位置和移动的距离来进行物体的旋转,并在鼠标释放后将物体恢复到初始旋转位置
♥️作者:白日参商 🤵♂️个人主页:白日参商主页 ♥️坚持分析平时学习到的项目以及学习到的软件开发知识,和大家一起努力呀!!! 🎈🎈加油! 加油!…...

金蝶软件实现导入Excel数据分录行信息到单据体分录行中
>>>适合KIS云专业版V16.0|KIS云旗舰版V7.0|K/3 WISE 14.0等版本<<< 金蝶软件中实现[导入Excel数据业务分录行]信息到[金蝶单据体分录]中,在采购订单|采购入库单|销售订单|销售出库单等类型单据中,以少量的必要字段在excel表格中按模板填列好,很方便快捷地从…...

C# 11 中的新增功能
本文内容 泛型属性泛型数学支持数值 IntPtr 和 UIntPtr字符串内插中的换行符 显示另外 11 个 C# 11 中增加了以下功能: 原始字符串字面量泛型数学支持泛型属性UTF-8 字符串字面量字符串内插表达式中的换行符列表模式文件本地类型必需的成员自动默认结构常量 str…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

篇章二 论坛系统——系统设计
目录 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 1. 数据库设计 1.1 数据库名: forum db 1.2 表的设计 1.3 编写SQL 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 通过需求分析获得概念类并结合业务实现过程中的技术需要&#x…...

Python 高级应用10:在python 大型项目中 FastAPI 和 Django 的相互配合
无论是python,或者java 的大型项目中,都会涉及到 自身平台微服务之间的相互调用,以及和第三发平台的 接口对接,那在python 中是怎么实现的呢? 在 Python Web 开发中,FastAPI 和 Django 是两个重要但定位不…...
