邮递员送信 单源最短路+反向建边
有一个邮递员要送东西,邮局在节点 1 1 1。他总共要送 n − 1 n−1 n−1样东西,其目的地分别是节点 2 2 2到节点 n n n。所有的道路都是单行的,共有 m m m条道路。邮递员每次只能带一样东西,运送每件物品过后必须返回邮局。求送完东西后回到邮局最少需要的时间。
首先送信时,从 1 1 1到 2 − n 2-n 2−n就是标准的单源最短路;而返回的时候就是多到一,多源最短路比较麻烦。这时候我们邻接矩阵倒过来,从多到一的最短路变式的路径“反向建边”,就变成一到多的单源最短路。
#include<bits/stdc++.h>
using namespace std;
struct node
{int u,v,w,next;
}a[100010],b[100010];
struct New
{int w,now;bool operator <(const New &x)const{return w>x.w;}
};
priority_queue <New> q;
int head[10010],bhead[10010],dis[10010],flag[10010];
int n,m,s,num1,num2,ans=0,x,y;
void add(int u,int v,int w)
{a[++num1].v=v;a[num1].w=w;a[num1].next=head[u];head[u]=num1;b[++num2].v=u;b[num2].w=w;b[num2].next=bhead[v];bhead[v]=num2;
}
void Dij()
{for(int i=1;i<=n;i++)dis[i]=9999999;dis[1]=0;memset(flag,0,sizeof(flag));q.push((New){0,1});while(!q.empty()){New X=q.top();q.pop();int U=X.now;if(flag[U]==1)continue;flag[U]=1;for(int i=head[U];i;i=a[i].next){int V=a[i].v;if(dis[V]>dis[U]+a[i].w){dis[V]=dis[U]+a[i].w;q.push((New){dis[V],V});}}}
}
void Dij2()
{for(int i=1;i<=n;i++)dis[i]=9999999;memset(flag,0,sizeof(flag));dis[1]=0;q.push((New){0,1});while(!q.empty()){New X=q.top();q.pop();int U=X.now;if(flag[U]==1)continue;flag[U]=1;for(int i=bhead[U];i;i=b[i].next){int V=b[i].v;if(dis[V]>dis[U]+b[i].w){dis[V]=dis[U]+b[i].w;q.push((New){dis[V],V});}}}
}
int main()
{cin>>n>>m;for(int i=1;i<=m;i++){cin>>x>>y>>s;add(x,y,s);}Dij();for(int i=2;i<=n;i++)ans+=dis[i];Dij2();for(int i=2;i<=n;i++)ans+=dis[i];cout<<ans<<endl;return 0;
}
相关文章:

邮递员送信 单源最短路+反向建边
有一个邮递员要送东西,邮局在节点 1 1 1。他总共要送 n − 1 n−1 n−1样东西,其目的地分别是节点 2 2 2到节点 n n n。所有的道路都是单行的,共有 m m m条道路。邮递员每次只能带一样东西,运送每件物品过后必须返回邮局。求送完东…...

git的常用操作
1. git查看dev分支与master分支的情况 要查看特定分支(如dev和master)的情况,您可以使用以下命令: git log --oneline master..dev 这将显示在dev分支上存在但不在master分支上的提交记录的简要信息。每条记录都包括提交的哈希…...
vscode搭建java开发环境
一、配置extensions环境变量VSCODE_EXTENSIONS, 该环境变量路径下的存放安装组件: 二、setting配置文件 {"java.jdt.ls.java.home": "e:\\software\\jdk\\jdk17",// java运行环境"java.configuration.runtimes": [{"…...

01 qt快速入门
一 qt介绍 1.基本概念 1991年由Qt Company(奇趣)开发的跨平台C++图形用户界面应用程序开发框架,GUI程序和非GUI程序。优点:一套源码在不同的平台通过不同的编译器进行编译,就可以运行到该平台上目标机。面向对象的封装机制来对其接口封装。 GUI —图形用户界面(Graphic…...

嵌入式开发中常用且杂散的命令
1、mount命令 # 挂载linux系统 mkdir /tmp/share mount -t nfs 10.77.66.88:/share/ /tmp/share -o nolock,tcp cd /tmp/share# 挂载Windows系统 mkdir /tmp/windows mount -t nfs 10.66.77.88:/c/public /tmp/windows -o nolock,tcp cd /tmp/windows# 挂载vfat格式的U盘 mkdi…...

JS导出复杂多级表头的Excel
使用方式 1、安装依赖 npm install xlsx-js-style2、复制代码文件exportExcel.js至工程 https://github.com/EnthuDai/export-excel-in-one-line 3、在引入excel.js后调用 Excel.export(columns, dataSource, 导出文件名)4、代码demo 5、效果 页面excel 适用范围 对于使…...

2023国赛数学建模E题思路分析
文章目录 0 赛题思路1 竞赛信息2 竞赛时间3 建模常见问题类型3.1 分类问题3.2 优化问题3.3 预测问题3.4 评价问题 4 建模资料 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 竞赛信息 全国大学生数学建模…...

【JavaScript 12】二进制位运算符 或 与 非 异或 左移 右移 头部补零右移
二进制位运算符 概述 概述 7个用于直接对二进制位进行运算 二进制或 or | 若两个二进制位都为0则为0,否则为1二进制与 and & 若两个二进制位都为1则为1,否则为0二进制非 not ~ 对一个二进制位取反异或 xor ^ 若两个二进制位不同则为1,否…...

Kafka 入门到起飞 - Kafka是怎么保证可靠性的呢
在这里插入图片描述 我们已经了解到,复习一下 创建topic时,可以指定副本因子 repilication-factor 3 表示分区的副本数,包括Leader分区副本和follower分区副本不要超过broker的数量,尽量保证一个分区的副本均匀分散不同的broker…...

数学建模(三)整数规划
视频推荐:B站_数学建模老哥 一、整数规划基本原理 数学规划中的变量(部分或全部)限制为整数时,称为整数规划。若在线性规划模型中,变量限制为整数,则称为整数线性规划。目前所流行的求解整数规划的方法&am…...

全面梳理Python下的NLP 库
一、说明 Python 对自然语言处理库有丰富的支持。从文本处理、标记化文本并确定其引理开始,到句法分析、解析文本并分配句法角色,再到语义处理,例如识别命名实体、情感分析和文档分类,一切都由至少一个库提供。那么,你…...

系统设计类题目汇总三
20 秒杀系统的一些拓展和优化 20.1 你发送消息时,流程是将消息发送给MQ做异步处理,然后消费者去消费消息,之后调用运营商的发送消息接口,那如果调用运营商的接口后消息发送失败怎么办? 确实,对于这种核心…...

“深入解析JVM:探索Java虚拟机的内部工作原理“
标题:深入解析JVM:探索Java虚拟机的内部工作原理 摘要:本文将深入解析Java虚拟机(JVM)的内部工作原理,包括类加载、内存管理、垃圾回收、即时编译等关键概念。通过对这些概念的详细讲解和示例代码的演示&a…...

VB+sql小型超市管理系统设计与实现
1、项目计划 1.1系统开发目的 (1)大大提高超市的运作效率; (2)通过全面的信息采集和处理,辅助提高超市的决策水平; (3)使用本系统,可以迅速提升超市的管理水平,为降低经营成本, 提高效益,增强超市扩张力, 提供有效的技术保障。 1.2背景说明 21世纪,超市的…...

mysql面试
基础篇 通用语法及分类 DDL: 数据定义语言,用来定义数据库对象(数据库、表、字段)DML: 数据操作语言,用来对数据库表中的数据进行增删改DQL: 数据查询语言,用来查询数据库中表的记录DCL: 数据控制语言,用…...

3.1 Ansible 的使用和配置管理
Ansible 的使用和配置管理 文章目录 Ansible 的使用和配置管理Ansible 基础Ansible 模块和变量主机管理和组织角色和剧本部署应用和配置自动化与批量操作Ansible 常见用例Ansible 最佳实践和性能优化 大纲 Ansible 简介和特点 介绍 Ansible 的定义和作用,以及它在配…...

神经网络基础-神经网络补充概念-06-计算图
概念 “计算图”(Computational Graph)是一种用于表示数学表达式计算过程的图结构,广泛用于深度学习和自动微分等领域。计算图将复杂的数学表达式分解为一系列简单的计算节点,这些节点之间通过边连接,形成了一个有向无…...
【【STM32之GPIO】】
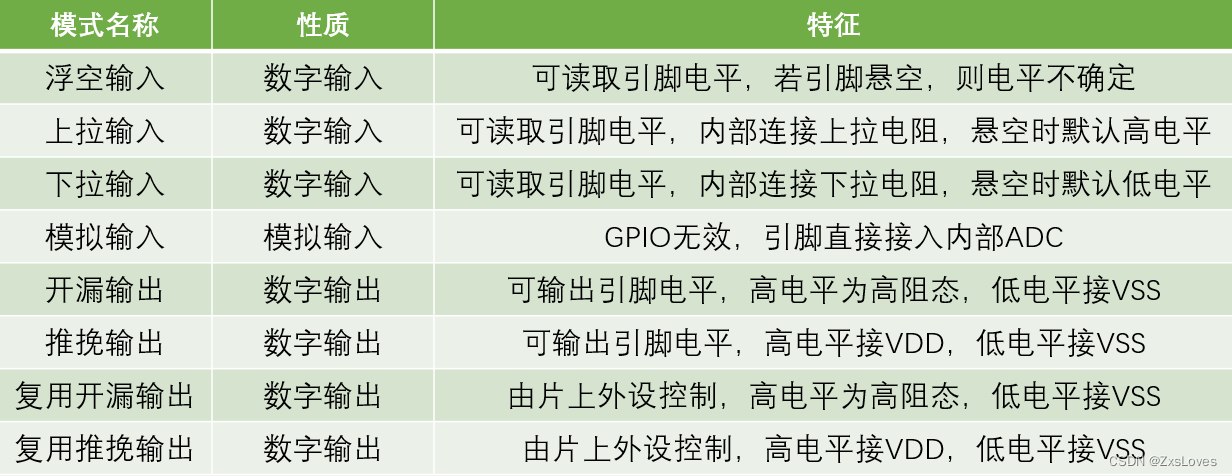
STM32之GPIO 学完了正点原子自带的视频课之后感觉仍然一知半解现在更新一下来自其他版本的STM32学习 GPIO 就是 General Purpose Input Output 中文名叫通用输入输出口 可配置8种输入输出模式 引脚电平 0V~3.3V 部分引脚可容忍5V 输出模式下可控制端口输出高低电平ÿ…...
【动画】p60动画蓝图、播放蒙太奇、打包
p60动画蓝图、播放蒙太奇、打包 p60动画蓝图、播放蒙太奇、打包添加动画动画蓝图使模型使用动画蓝图奔跑跳舞蒙太奇 移动打断蒙太奇打包退出游戏 p60动画蓝图、播放蒙太奇、打包 添加动画 右键内容浏览器-》动画-》混合空间1D-》选择新的角色的骨骼 如下图在资产详情修改参数…...
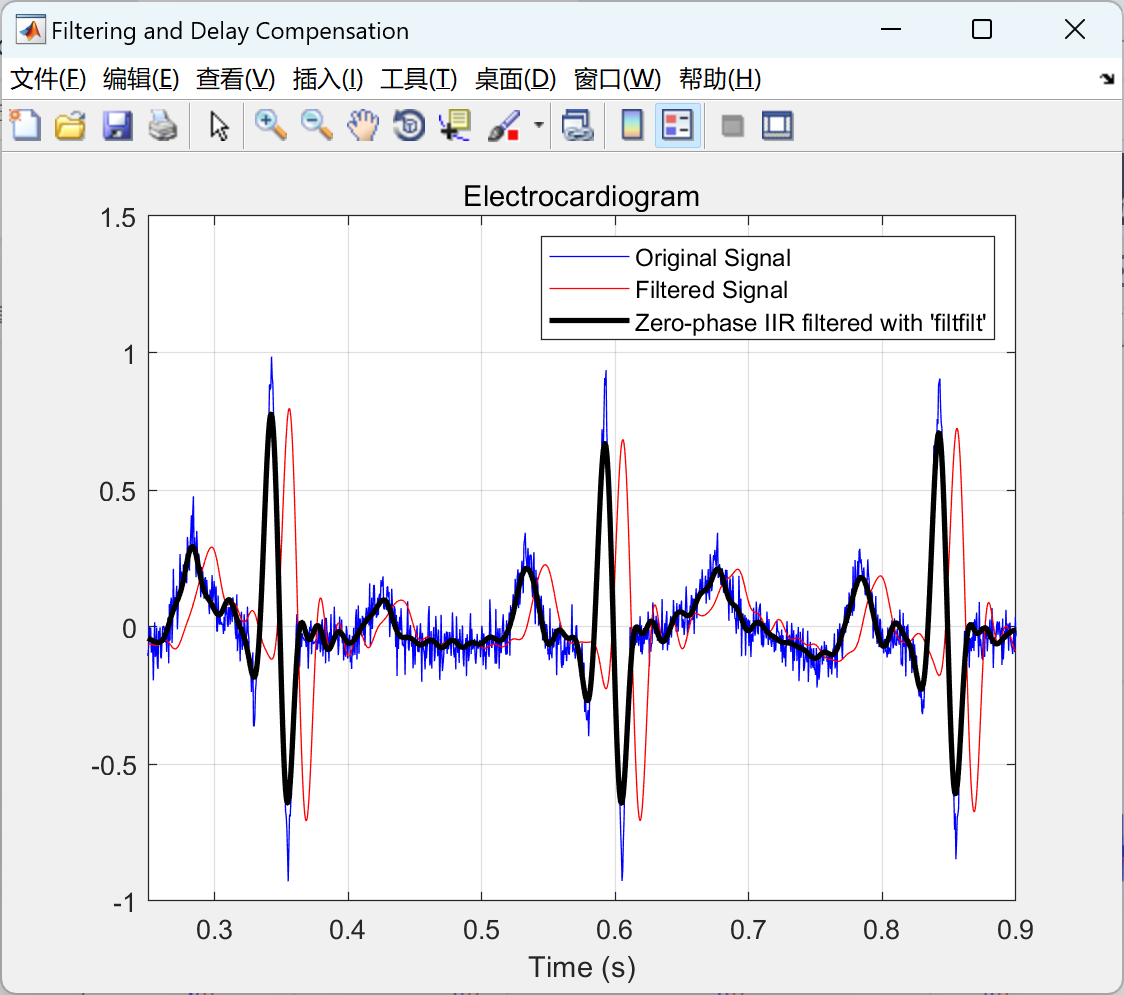
去趋势化一个心电图信号、信号功率谱、低通IIR滤波器并平滑信号、对滤波器引起的延迟进行补偿研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...

【Kafka】Kafka从入门到实战:构建高吞吐量分布式消息系统
Kafka从入门到实战:构建高吞吐量分布式消息系统 一、Kafka概述 Apache Kafka是一个分布式流处理平台,最初由LinkedIn开发,后成为Apache顶级项目。它被设计用于高吞吐量、低延迟的消息处理,能够处理来自多个生产者的海量数据,并将这些数据实时传递给消费者。 Kafka核心特…...
与文本切分器(Splitter)详解《二》)
LangChain 中的文档加载器(Loader)与文本切分器(Splitter)详解《二》
🧠 LangChain 中 TextSplitter 的使用详解:从基础到进阶(附代码) 一、前言 在处理大规模文本数据时,特别是在构建知识库或进行大模型训练与推理时,文本切分(Text Splitting) 是一个…...
