十面骰子、
十面骰子(一):
v 有一个十面的骰子,每一面分别为1-10,不断投掷骰子,投10000次,统计每一面1-10出现的次数或概率.
v 提示:可用rand()产生1-10之间的随机数,再统计1-10出现的机会,存放于数组里,如count[1]存放点数为1的次数,如count[2]存放点数为2的次数
十面骰子(二):
v 有一个十面的骰子,每一面分别为1-10,不断投掷骰子,直到骰子上的数累计和超过100停止,问这个和最可能的是哪个数?平均要投掷多少次?
v 玩一次游戏:
v 需要多次抛掷,直到点数和超过100.
v 十面的骰子,每次抛得的点数:p=rand()%10+1
v 累加和点数:sum = sum +p
v if sum>100 stop 抛掷
v 求sum 以及得到这个sum所抛掷的次数
v 以上游戏反复10000次。
分析:
10000次游戏结束后:
统计所得到点数的和的次数?sum可能的结果范围是101-110.可定义一个sum[110](也可定义两个数组分别存放抛到和的次数和抛到和所用的次数),数组元素sum[101]表示在10000次中,抛掷得到点数和为101的次数,sum[110]表示在10000次中,抛掷得到点数和为110的次数……
得到点数和超过100这样的结果,要投掷多少次?可能投掷的次数范围是11-101次,也可用数组来存放,如数组元素sum[11]表示抛掷了11次就得到和超过100,在10000次游戏中,有多少次?
(一)代码
#include <iostream>
#include <stdlib.h>
#include <time.h>
using namespace std;
int main()
{int count[11] = { 0 };int i;srand((unsigned)time(NULL));for (i = 1; i <= 10000; i++){count[rand() % 10 + 1]++;}for (i = 1; i <= 10; i++){cout << "投到面" << i << "的次数是:" << count[i] << endl;//cout << "投到面" << i << "的概率是:" << count[i] / 10000;//cout << endl;}return 0;
}(二)代码
#include <iostream>
#include <iomanip>
#include <stdlib.h>
#include <time.h>
using namespace std;
int main()
{int count[102] = { 0 }, Sum[111] = { 0 }; //count[102]用来装10000次游戏每次要投掷到累积点数超过100的次数,Sum[111]用来装10000次游戏每次投掷后累积点数超过100后的具体累积点数int i,p,sum,n; //sum是一次游戏的累积点数,n是一次游戏的投掷次数 srand((unsigned)time(NULL));for (i = 1; i <= 10000; i++) //重复10000次游戏{sum = 0, n = 0;while (1){p = rand() % 10 + 1;sum += p;n++;if (sum > 100)break;}count[n]++;Sum[sum]++;}cout << "统计所得到的点数的和的次数?" << endl;for (i = 101; i <= 110; i++){cout << "累积点数和为 " << i << " , 投到该点数和的次数为 " << Sum[i] << endl;}cout << endl;cout << "得到点数和超过100这样的结果,要投掷多少次?" << endl;cout << " 得到点数和超过100时投掷的次数 " << "投掷了该次数点数和才超过100的游戏次数" << endl;for (i = 11; i <= 101; i++){cout <<setw(4)<< i <<setw(36)<< count[i] << endl;;}return 0;
}相关文章:

十面骰子、
十面骰子(一): v 有一个十面的骰子,每一面分别为1-10,不断投掷骰子,投10000次,统计每一面1-10出现的次数或概率. v 提示:可用rand()产生1-10之间的随机数,再统计1-10出现的机会,存放于数组里,…...
IDE的下载和使用
IDE 文章目录 IDEJETBRAIN JETBRAIN 官网下载对应的ide 激活方式 dxm的电脑已经把这个脚本下载下来了,脚本是macjihuo 以后就不用买了...

华为OD机试真题【字母组合】
1、题目描述 【字母组合】 数字0、1、2、3、4、5、6、7、8、9分别关联 a~z 26个英文字母。 0 关联 “a”,”b”,”c” 1 关联 “d”,”e”,”f” 2 关联 “g”,”h”,”i” 3 关联 “j”,”k”,”l” 4 关联 “m”,”n”,”o” 5 关联 “p”,”q”,”r” 6 关联 “s”,”t” 7…...
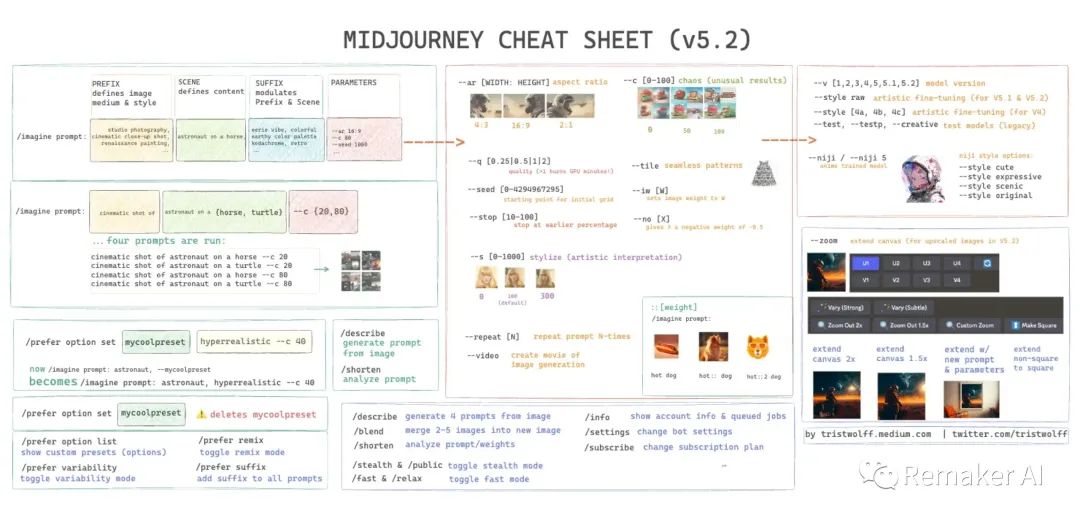
Midjourney Prompt 提示词速查表 v5.2
Midjourney 最新的版本更新正不断推出令人兴奋的新功能。这虽然不断扩展了我们的AI绘图工具箱,但有时也会让我们难以掌握所有实际可以使用的功能和参数。 针对此问题, 小编整理了 "Midjourney Prompt 提示词速查表",这是一个非常方便的 Midjo…...

自动驾驶——驶向未来的革命性技术
自动驾驶——驶向未来的革命性技术 自动驾驶的组件自动驾驶的优势自动驾驶的应用自动驾驶的未来中国的自动驾驶 自动驾驶是一种技术,它允许车辆在没有人类驾驶员的情况下自主地进行行驶。它利用各种传感器、计算机视觉、人工智能和机器学习算法来感知和理解周围环境…...
 甲级 1004 Counting Leaves)
PAT (Advanced Level) 甲级 1004 Counting Leaves
点此查看所有题目集 A family hierarchy is usually presented by a pedigree tree. Your job is to count those family members who have no child. Input Specification: Each input file contains one test case. Each case starts with a line containing 0<N<100, …...
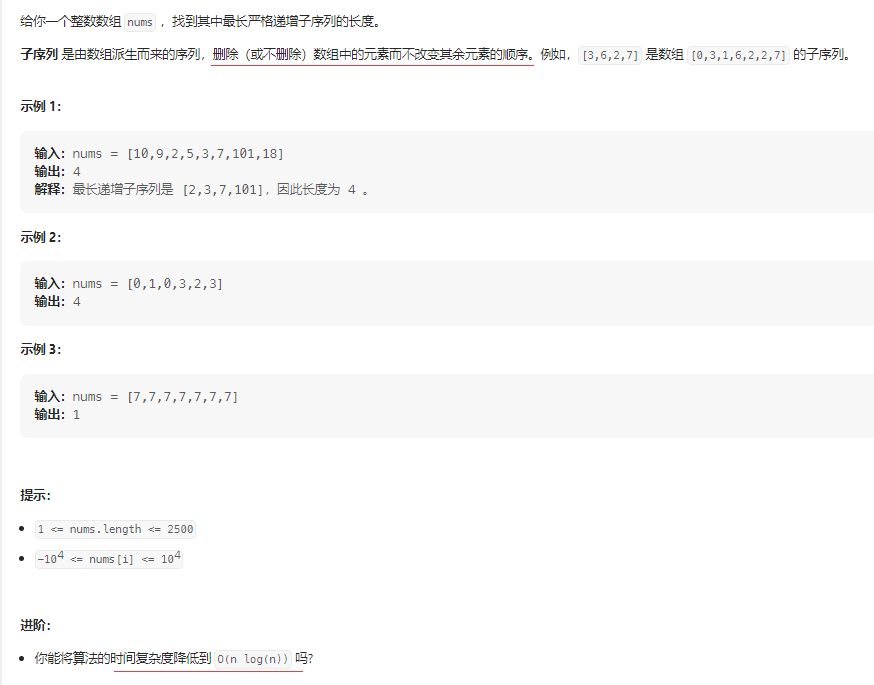
最长递增子序列——力扣300
int lengthOfLIS(vector<int>& nums) {int len=1, n=nums.size();if...

邮递员送信 单源最短路+反向建边
有一个邮递员要送东西,邮局在节点 1 1 1。他总共要送 n − 1 n−1 n−1样东西,其目的地分别是节点 2 2 2到节点 n n n。所有的道路都是单行的,共有 m m m条道路。邮递员每次只能带一样东西,运送每件物品过后必须返回邮局。求送完东…...

git的常用操作
1. git查看dev分支与master分支的情况 要查看特定分支(如dev和master)的情况,您可以使用以下命令: git log --oneline master..dev 这将显示在dev分支上存在但不在master分支上的提交记录的简要信息。每条记录都包括提交的哈希…...
vscode搭建java开发环境
一、配置extensions环境变量VSCODE_EXTENSIONS, 该环境变量路径下的存放安装组件: 二、setting配置文件 {"java.jdt.ls.java.home": "e:\\software\\jdk\\jdk17",// java运行环境"java.configuration.runtimes": [{"…...

01 qt快速入门
一 qt介绍 1.基本概念 1991年由Qt Company(奇趣)开发的跨平台C++图形用户界面应用程序开发框架,GUI程序和非GUI程序。优点:一套源码在不同的平台通过不同的编译器进行编译,就可以运行到该平台上目标机。面向对象的封装机制来对其接口封装。 GUI —图形用户界面(Graphic…...

嵌入式开发中常用且杂散的命令
1、mount命令 # 挂载linux系统 mkdir /tmp/share mount -t nfs 10.77.66.88:/share/ /tmp/share -o nolock,tcp cd /tmp/share# 挂载Windows系统 mkdir /tmp/windows mount -t nfs 10.66.77.88:/c/public /tmp/windows -o nolock,tcp cd /tmp/windows# 挂载vfat格式的U盘 mkdi…...

JS导出复杂多级表头的Excel
使用方式 1、安装依赖 npm install xlsx-js-style2、复制代码文件exportExcel.js至工程 https://github.com/EnthuDai/export-excel-in-one-line 3、在引入excel.js后调用 Excel.export(columns, dataSource, 导出文件名)4、代码demo 5、效果 页面excel 适用范围 对于使…...

2023国赛数学建模E题思路分析
文章目录 0 赛题思路1 竞赛信息2 竞赛时间3 建模常见问题类型3.1 分类问题3.2 优化问题3.3 预测问题3.4 评价问题 4 建模资料 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 竞赛信息 全国大学生数学建模…...

【JavaScript 12】二进制位运算符 或 与 非 异或 左移 右移 头部补零右移
二进制位运算符 概述 概述 7个用于直接对二进制位进行运算 二进制或 or | 若两个二进制位都为0则为0,否则为1二进制与 and & 若两个二进制位都为1则为1,否则为0二进制非 not ~ 对一个二进制位取反异或 xor ^ 若两个二进制位不同则为1,否…...

Kafka 入门到起飞 - Kafka是怎么保证可靠性的呢
在这里插入图片描述 我们已经了解到,复习一下 创建topic时,可以指定副本因子 repilication-factor 3 表示分区的副本数,包括Leader分区副本和follower分区副本不要超过broker的数量,尽量保证一个分区的副本均匀分散不同的broker…...

数学建模(三)整数规划
视频推荐:B站_数学建模老哥 一、整数规划基本原理 数学规划中的变量(部分或全部)限制为整数时,称为整数规划。若在线性规划模型中,变量限制为整数,则称为整数线性规划。目前所流行的求解整数规划的方法&am…...

全面梳理Python下的NLP 库
一、说明 Python 对自然语言处理库有丰富的支持。从文本处理、标记化文本并确定其引理开始,到句法分析、解析文本并分配句法角色,再到语义处理,例如识别命名实体、情感分析和文档分类,一切都由至少一个库提供。那么,你…...

系统设计类题目汇总三
20 秒杀系统的一些拓展和优化 20.1 你发送消息时,流程是将消息发送给MQ做异步处理,然后消费者去消费消息,之后调用运营商的发送消息接口,那如果调用运营商的接口后消息发送失败怎么办? 确实,对于这种核心…...

“深入解析JVM:探索Java虚拟机的内部工作原理“
标题:深入解析JVM:探索Java虚拟机的内部工作原理 摘要:本文将深入解析Java虚拟机(JVM)的内部工作原理,包括类加载、内存管理、垃圾回收、即时编译等关键概念。通过对这些概念的详细讲解和示例代码的演示&a…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

离线语音识别方案分析
随着人工智能技术的不断发展,语音识别技术也得到了广泛的应用,从智能家居到车载系统,语音识别正在改变我们与设备的交互方式。尤其是离线语音识别,由于其在没有网络连接的情况下仍然能提供稳定、准确的语音处理能力,广…...

绕过 Xcode?使用 Appuploader和主流工具实现 iOS 上架自动化
iOS 应用的发布流程一直是开发链路中最“苹果味”的环节:强依赖 Xcode、必须使用 macOS、各种证书和描述文件配置……对很多跨平台开发者来说,这一套流程并不友好。 特别是当你的项目主要在 Windows 或 Linux 下开发(例如 Flutter、React Na…...
