数据结构—图的应用
6.4图的应用
概念回顾—生成树
生成树:所有顶点均由边连接在一起,但不存在回路的图。
- 一个图可以有许多棵不同的生成树、
- 含有n个顶点 n-1 条边的图不一定是生成树
- 所有生成树具有以下共同特点
- 生成树的顶点个数与图的顶点个数相同;
- 生成树是图的极小连通子图,去掉一条边则非连通;
- 一个有n个顶点的连通图的生成树有 n-1 条边;
- 在生成树中再加一条边必然形成回路。
- 生成树中任意两个顶点间的路径是唯一的;
6.4.1无向图的生成树
设图G=(V,E)是个连通图,当从图任一顶点出发遍历图G时,将边集E(G)分层两个集合T(G)和B(G)。其中T(G)是遍历图时所经过的边的集合,B(G)是遍历图时未经过的边的集合。显然,G1(V,T)是图G的极小连通子图。即子图G1是连通图G的生成树。
6.4.2最小生成树
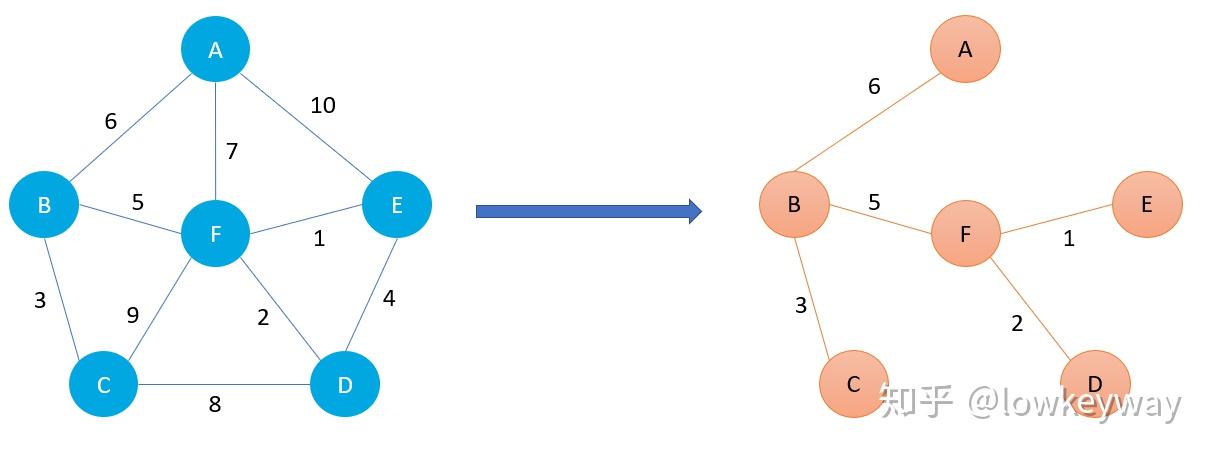
最小生成树:给定一个无向网络,在该网的所有生成树中,使得各边权值之和最小的那棵生成树成为该网的最小生成树,也叫最小代价生成树。
1、构造最小生成树
构造最小生成树的算法很多,其中多数算法都利用了MST的性质。
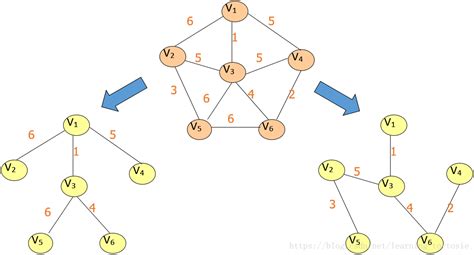
MST性质:设N=(V,E)是一个连通网,U是顶点集V的一个非空子集。若边(u,v)是一条具有最小权值的边,其中u∈U,v∈V-U,则必存在一棵包含边(u,v)的最小生成树。
MST性质解释:
在生成树的构造过程中,图中n个顶点分属两个集合:
-
已落在生成树上的顶点集:U
-
尚未落在生成树上的顶点集:V-U
接下来则应在所有连通U中顶点和V-U中顶点的边中选取权值最小的边。
2、构造最小生成树算法
普里姆(Prim)算法
算法思想:
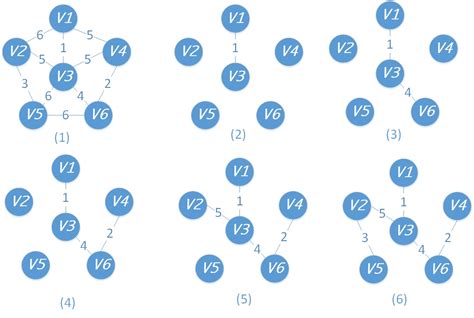
- 设N=(V,E)是连通网,TE是N上最小生成树中边的集合。
- 初始令U={u0},(u0∈V),TE={}。
- 在所有u∈U,v∈V-U的边(u,v)∈E中,找一条代价最小的边(u0,v0)。
- 将(u0,v0)并入集合TE,同时v0并入U。
- 重复上述操作直至U=V为止,则T=(V,TE)为N的最小生成树。
克鲁斯卡尔(Kruskal)算法
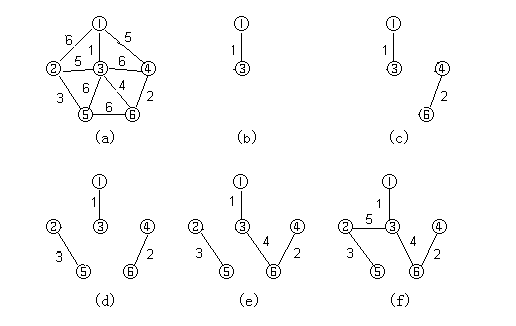
算法思想:
- 设连通图N=(V,E),令最小生成树初始状态只有n个顶点而无边的非连通图T=(V,{}),每个顶点自成一个连通分量。
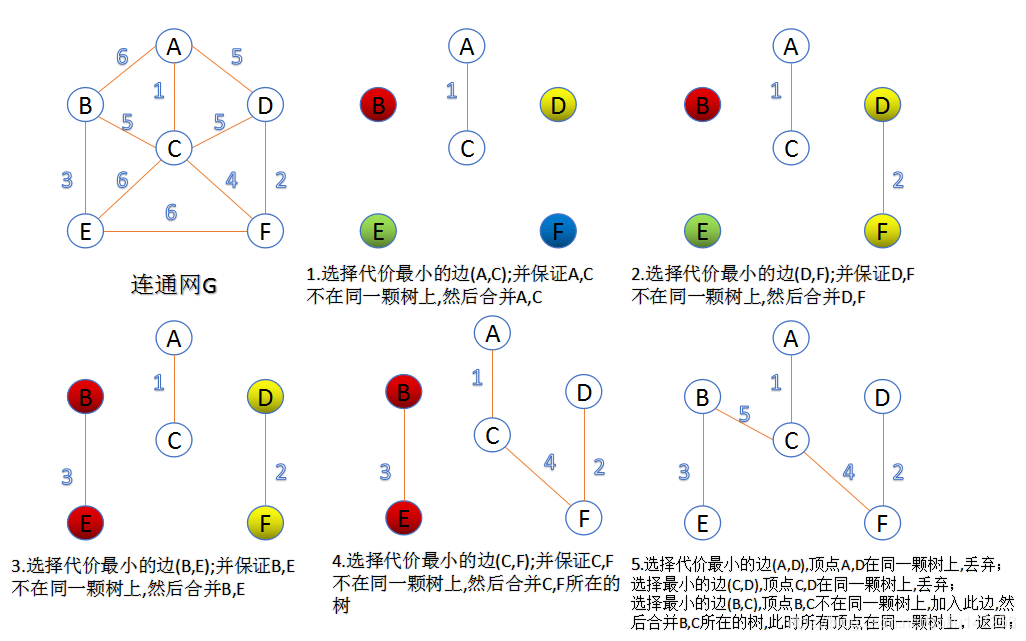
- 在E中选取代价最小的边,若该边依附的顶点落在T中不同的连通分量上(即:不能形成环),则将此边加入到T中;否则,舍去此边,选取下一条代价最小的边。
- 依此类推,直至T中所有顶点都在同一连通分量上为止。
最小生成树可能不唯一
两种算法比较
| 算法名 | 普里姆算法 | 克鲁斯卡尔算法 |
|---|---|---|
| 算法思想 | 选择点 | 选择边 |
| 时间复杂度 | O(n2) (n为顶点数) | O(eloge) (e为边数) |
| 适应范围 | 稠密图 | 稀疏图 |
6.4.3最短路径
典型用途:交通网络的问题—从甲地到乙地之间是否有公路连通?在有多条通路的情况下,哪一条路最短?
交通网络用有向网来表示:
顶点——表示地点
弧——表示两个地点有路连通,
弧上的权值——表示两地点之间的距离,交通费或途中所花费的时间等。
如何能够使一个地点到另一个地点的运输时间最短或运费最省?这就是一个求两个地点间的最短路径问题。
问题抽象:在有向网中A点(源点)到达B点(终点)的多条路径中个,寻找一条各边权值之和最小的路径,即最短路径。
最短路径与最小生成树不同,路径上不一定包含n个顶点,也不一定包含n-1条边。
第一类问题:两点间最短路径
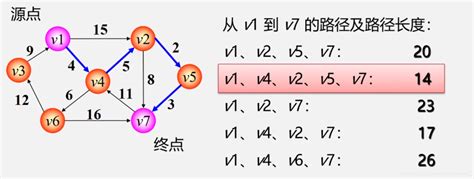
第二类问题:某源点到其他各点最短路径

![[最短路径问题]Dijkstra算法(含还原具体路径) - 技术经验 - W3xue](https://img-blog.csdnimg.cn/img_convert/ad9283be681ef22415e09b470390e446.jpeg)
两种常见的最短路径问题:
- 单源最短路径—用**Dijkstra(迪杰斯特拉)**算法
- 所有顶点间的最短路径—用**Floyd(弗洛伊德)**算法
1、Dijkstra算法
-
初始化:先找出从源点v0到各终点vk的直达路径(v0,vk),即通过一条弧到达的路径。
-
选择:从这些路径中找出一条长度最短的路径(v0,u)
-
更新:然后对其余各条路径进行适当的调整:
- 若在图中存在弧(u,vk),且(v0,u)+(u,vk)<(v0,vk),则以路径(v0,u,vk)代替(v0,vk)。
-
在调整后的各条路径中,再找长度最短的路径,依此类推。
迪杰斯特拉(Dijkstra)算法:按路径长度递增次序产生最短路径。
-
把V分成两组:
- S:已求出最短路径的顶点的集合。
- T=V-S:尚未确定最短路径的顶点集合。
-
将T中顶点按最短路径递增的次序加入到S中。
保证(1)从源点v0到S中各顶点的最短路径长度都不大于从v0到T中任何顶点的最短路径长度。
(2)每个顶点对应一个距离值:
S中顶点:从v0到此顶点的最短路径长度。
T中顶点:从v0到此顶点的只包括S中顶点作中间顶点的最短路径长度。
所有顶点间的最短路径:
方法一:每次以一个顶点为源点,重复执行Dijkstra算法n次。
方法二:弗洛伊德(Floyd)算法。
2、Floyd算法
算法思想:
- 逐个顶点试探
- 从vi到vj的所有可能存在的路径中
- 选出一条长度最短的路径
例如:采用Floyd算法,求图中各顶点之间最短路径
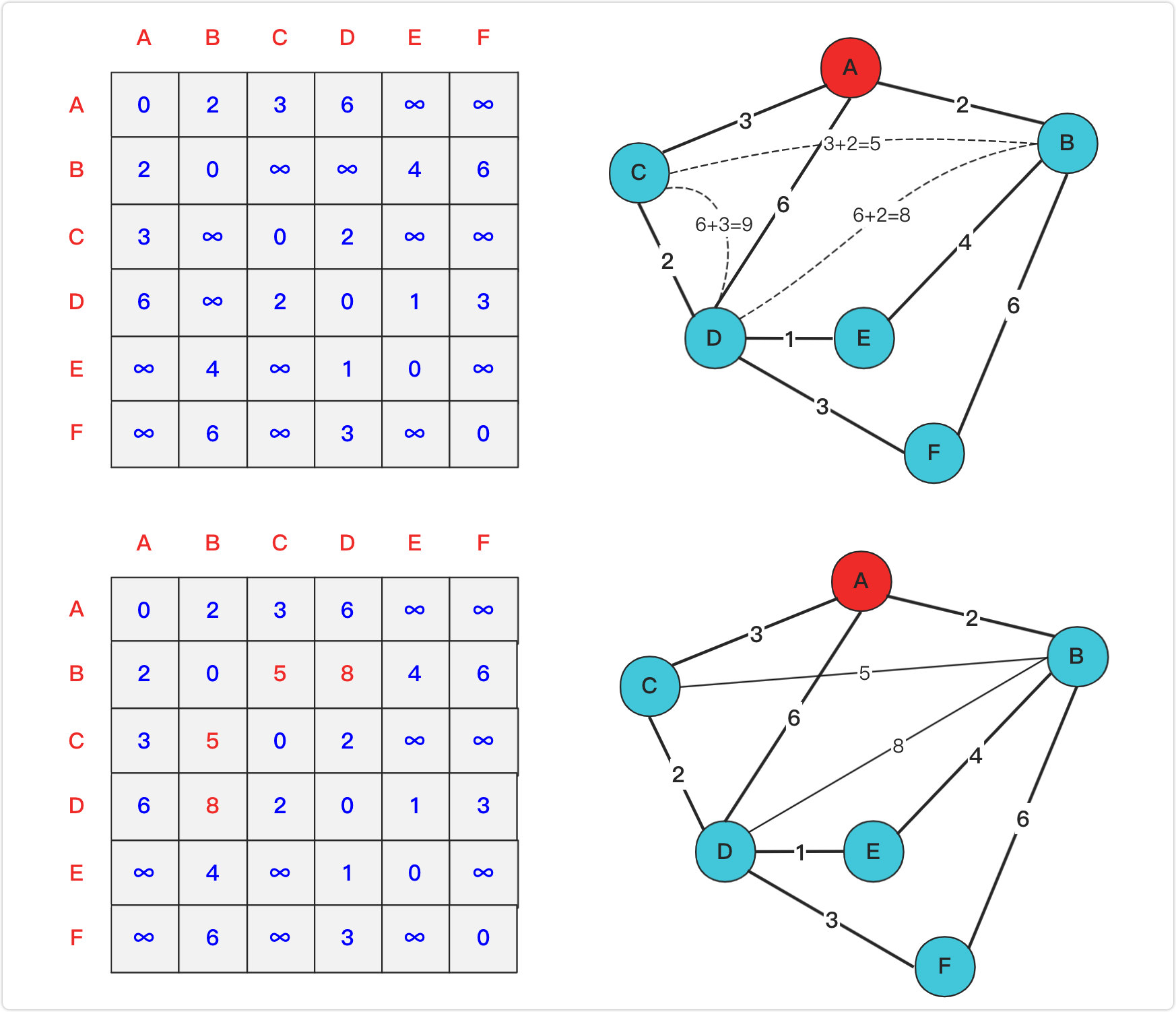
求最短路径步骤:
初始时设置一个n阶方阵,令其对角线元素为0,若存在弧<vi,vj>,则对应元素为权值,否则为∞
逐步试着在原直接路径中增加中间顶点,若加入中间顶点后路径变短,则修改之;否则,维持原值。所有顶点试探完毕,算法结束。
6.4.4拓扑排序
1、有向无环图
有向无环图:无环的有向图,简称DAG图(Directed Acycline Graph)
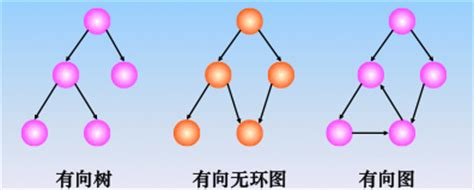
有向无环图常用来描述一个工程或系统的进行过程。(通常把计划、施工、生产、程序流程等当成是一个工程)
一个工程可以分为若干个子工程,只要完成了这些子工程(活动),就可以导致整个工程的完成。
**AOV网:**拓扑排序
用一个有向图表示一个工程的各子工程及其相互制约的关系,其中以顶点表示活动,弧表示活动之间的优先制约关系,称这种有向图为顶点表示活动的网,简称AOV网(Activity Vertex network)。
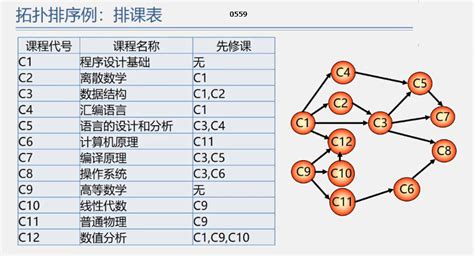
特点:
- 若从 i 到 j 有一条有向路径,则 i 是 j 的前驱;j 是 i 的后继。
- 若<i,j>是网中有向边,则 i 是 j 的直接前驱;j 是 i 的直接后继。
- AOV网中不允许有回路,因为如果有回路存在,则表明某项活动以自己为先决条件,显然这是荒谬的。
问题:如何判别AOV网中是否存在回路?
**AOE网:**关键路径
用一个有向图表示一个工程的各子工程及其相互制约的关系,以弧表示活动,以顶点表示活动的开始或结束事件,称这种有向图为边表示活动的网,简称为AOE网(Activity On Edge)。
拓扑排序
在AOV网没有回路的前提下,我们将全部活动排列成一个线性序列,使得若AOV网中有弧<i,j>存在,则在这个序列中,i 一定排在 j 的前面,具有这个性质的线性序列称为拓扑有序序列,相应的拓扑有序排序的算法称为拓扑排序。
拓扑排序的方法:
- 在有向图中选一个没有前驱的顶点且输出之。
- 从图中删除该顶点和所有以它为尾的弧。
- 重复上述两步,直至全部顶点均已输出;或者当图中不存在无前驱的顶点为止。

一个AOV网的拓扑序列不是唯一的
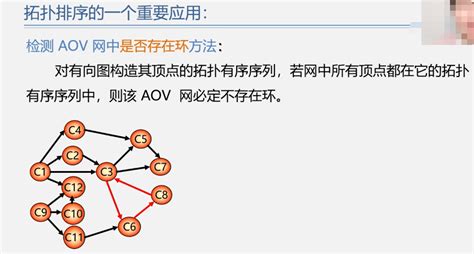
检测AOV网中是否存在环方法:
对有向图构造其顶点的拓扑有序序列,若网中所有顶点都在它的拓扑有序序列中,则该AOV网必定不存在环。
关键路径
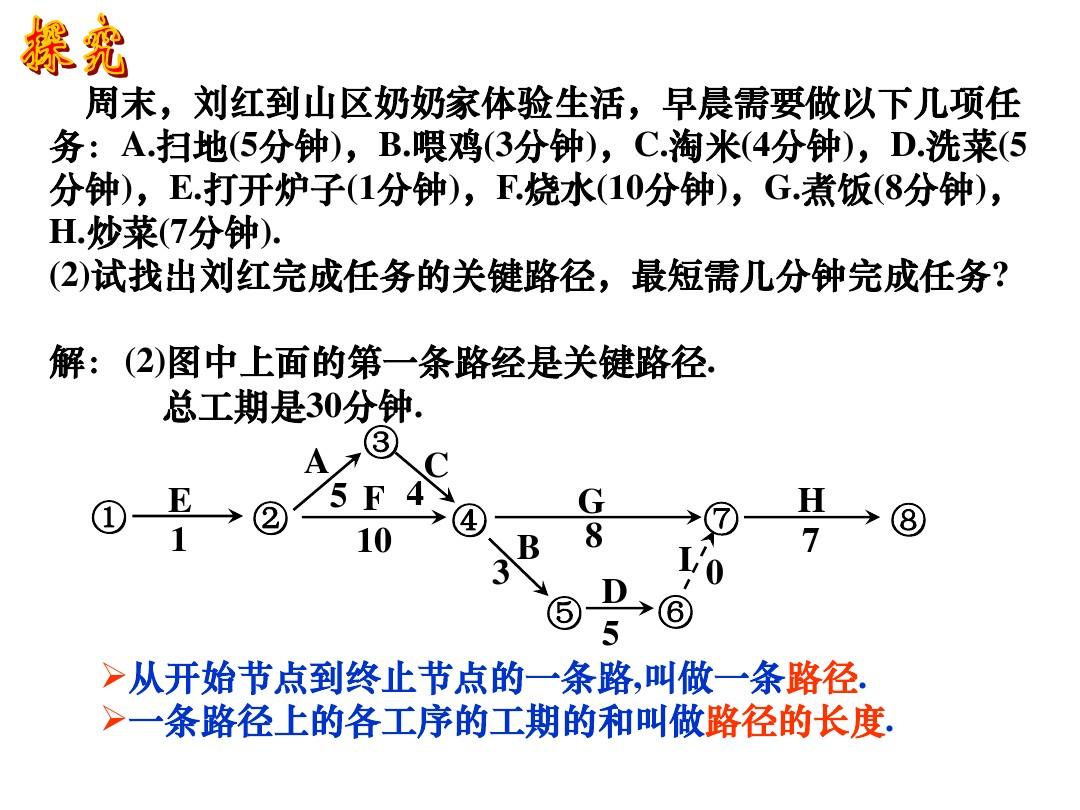
把工程计划表示为边表示活动的网络,即AOE网,用顶点表示事件,弧表示活动,弧的权表示活动持续时间。
事件表示在它之前的活动已经完成,在它之后的活动可以开始。
对于AOE网,我们关心两个问题:
- 完成整项工程至少需要多少时间?
- 那些活动是影响工程进度的关键?
关键路径——路径长度最长的路径。
路径长度——路径上各活动持续时间之和。
如何确定关键路径,需要定义4个描述量:
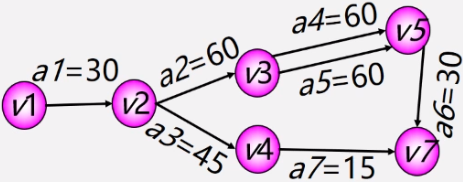
ve(vj)——表示事件 vj 的最早发生时间。
例如:ve(v1)=0 ve(v2)=30
vl(vj)——表示事件 vj 的最迟发生时间。
例如:vl(v4)=165
e(i)——表示活动 ai 的最早开始时间。
例如:e(a3)=30
l(i)——表示活动 ai 的最迟开始时间。
例如:l(a3)=120
l(i) - e(i)——表示完成活动 ai 的时间余量。
例如:l(3) - e(3)=90
关键活动——关键路径上的活动,即 l(i)==e(i)(即l(i) - e(i) == 0)的活动。

关键路径的讨论
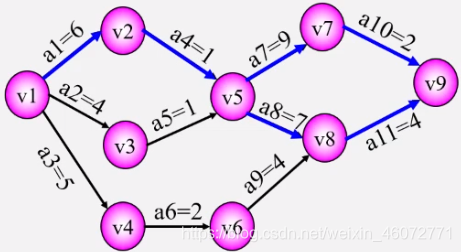
-
若网中有几条关键路径,则需加快同时在几条关键路径上的关键活动。
如:a11,a10,a8,a7。
-
如果一个活动处于所有的关键路径上,那么提高这个活动的速度,就能缩短整个工程的完成时间。如:a1、a4。
-
处于所有的关键路径上的活动完成时间不能缩短太多,否则会使原来的关键路径变成不是关键路径。这时,必须重新寻找关键路径。如:a1由6天变成3天,就会改变关键路径。
相关文章:

数据结构—图的应用
6.4图的应用 概念回顾—生成树 生成树:所有顶点均由边连接在一起,但不存在回路的图。 一个图可以有许多棵不同的生成树、含有n个顶点 n-1 条边的图不一定是生成树所有生成树具有以下共同特点 生成树的顶点个数与图的顶点个数相同;生成树是图的…...

Unity 鼠标控制 UI 放大、缩小、拖拽
文章目录 1. 代码2. 测试场景 1. 代码 using UnityEngine; using UnityEngine.UI; using UnityEngine.EventSystems;public class UIDragZoom : MonoBehaviour, IDragHandler, IScrollHandler {private Vector2 originalSize;private Vector2 originalPosition;private RectTr…...

tensorflow 模型计算中,预测错误;权重参数加载
tensorflow 模型计算中,预测错误;权重参数加载 tensorflow 模型计算主要代码(正确代码) linear1_kernel_initializer tf.constant_initializer(numpy.transpose(data["linear1.weight"])) linear1_bias_initializer …...

Jay17 2023.8.14日报 即 留校集训阶段性总结
8.14 打了moeCTF,还剩一题ak Web。 Jay17-集训结束阶段性总结: 集训产出: 自集训开始以来一个半月,最主要做的事情有三。 一是跟课程,复习学过的知识,学习新的知识;目前课程已大体听完&…...

【C语言】小游戏-扫雷(清屏+递归展开+标记)
大家好,我是深鱼~ 目录 一、游戏介绍 二、文件分装 三、代码实现步骤 1.制作简易游戏菜单 2. 初始化棋盘(11*11) 3.打印棋盘(9*9) 4.布置雷 5.计算(x,y)周围8个坐标的和 6.排查雷 <1>清屏后打印棋盘 <2>递归展开 <3>标记雷 四、完整代…...

云服务 Ubuntu 20.04 版本 使用 Nginx 部署静态网页
所需操作: 1.安装Nginx 2.修改配置文件 3.测试、重启 Nginx 4.内部修改防火墙 5.配置解析 6.测试是否部署成功 1.安装Nginx // 未使用 root 账号 apt-get update // 更新apt-get install nginx // 安装 nginx 1.1.测试是否安装没问题 在网页上输入云服务的公网…...

无后效性
动态规划的概念 在上例的多阶段决策问题中,各个阶段采取的决策,一般来说是与时间有关的,决策依赖于当前状态,又随即引起状态的转移,一个决策序列就是在变化的状态中产生出来的,故有“动态”的含义…...

Kubernetes系列-删除deployment和pod
通过deployment创建的pod直接执行delete是不会正常被删除的,因为deployment中设置了pod的数量,deployment会动态维护pod的数量,倘若pod数量少于约定数量,deployment会创建pod,直到pod数量达到约定数量才会停止。 如若…...

kotlin字符串方法
以下是一些常用的 String 方法示例: 1.获取字符串长度: val str "Hello, Kotlin" val length str.length2.字符串比较: val str1 "apple" val str2 "banana" val compareResult str1.compareTo(str2)3…...
ubuntu篇---配置FTP服务,本机和docker安装
ubuntu篇---配置FTP服务 一、本机安装1.1 安装FTP服务器软件1.2 配置FTP服务 二、docker安装(我用的这个)2.1 创建 目录2.2 启动脚本2.3 访问2.4 如何创建一个新的用户2.5 测试2.6 使用 一、本机安装 1.1 安装FTP服务器软件 ubuntu安装vsftp sudo apt…...
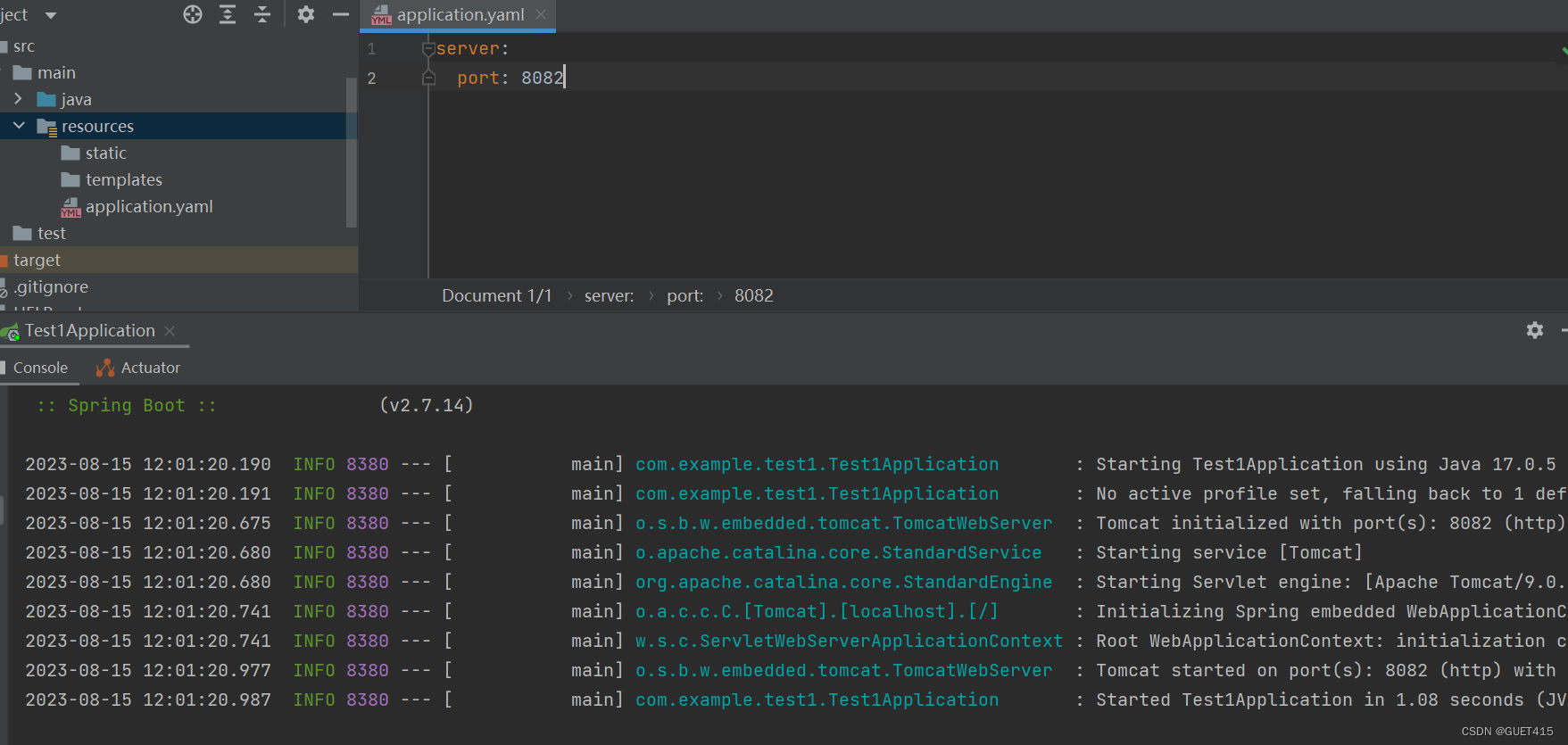
SpringBoot中properties、yml、yaml的优先级
原理 配置优先级低的会先加载然后会被配置优先级高的覆盖 验证 创建SpringBoot项目(网址) 在resource目录下创建application.properties、application.yml、application.yaml文件 运行 结论 优先级顺序: properties>yml>yaml...
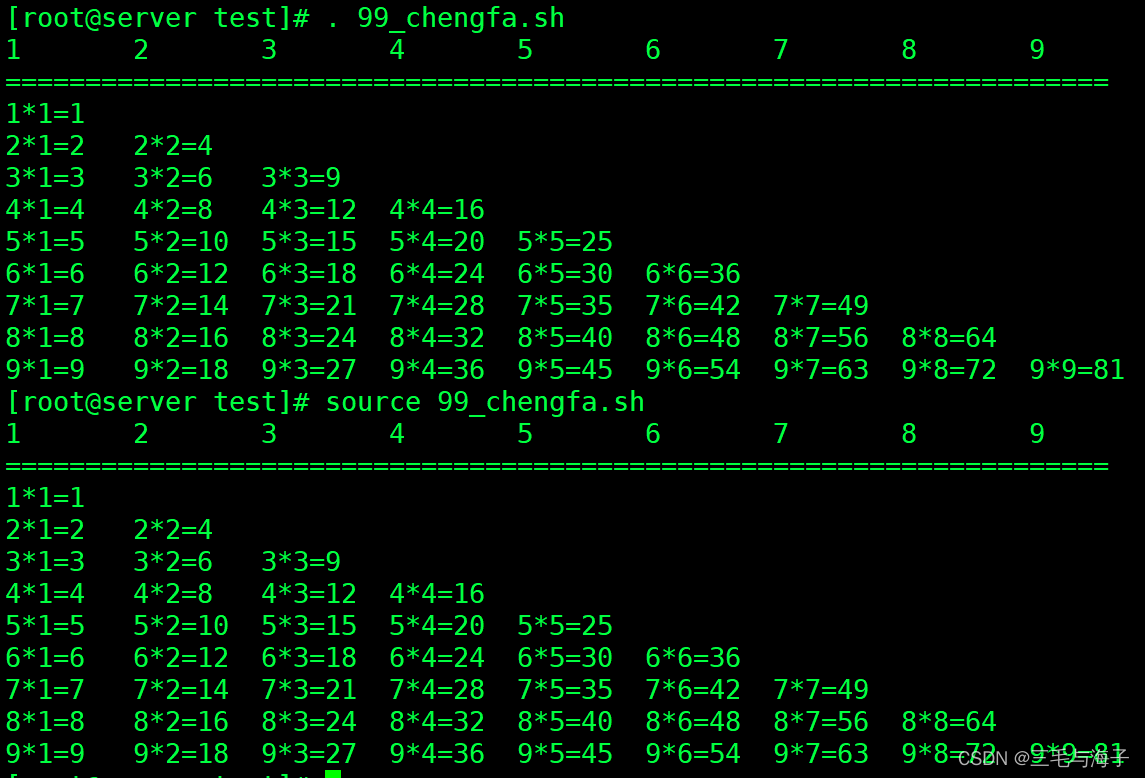
SHELL 基础 SHELL注释 及 执行SHELL脚本的四种方法
SHELL 脚本编写规范 : 脚本开头 : # 脚本第一行 : #! /bin/bash 或 #!/bin/sh ( 脚本解释器 ) # 程序段开头需要加 版本版权信息 ,例如 : # Date 创建日期 # Author : 作者 # …...

【Spring】深入探索 Spring AOP:概念、使用与实现原理解析
文章目录 前言一、初识 Spring AOP1.1 什么是 AOP1.2 什么是 Spring AOP 二、AOP 的核心概念2.1 切面(Aspect)2.2 切点(Pointcut)2.3 通知(Advice)2.4 连接点(Join Point) 三、Sprin…...

LocalDate介绍和使用
1.什么是 LocalDate? 在我们开始之前,让我先简单介绍一下 LocalDate。它是 Java 8 中引入的日期类,用于表示不带时区信息的日期。也就是说,它专注于日期,并忽略了具体的时间。这样,我们就可以专心解决那些…...

三、使用注解形式开发 Spring MVC程序
文章目录 一、环境准备二、配置 web.xml三、配置 SpringMVC-Servlet.xml ,这里不再使用之前那种写法,直接采用注解配置,引入注解支持,配置视图解析器四、编写 Controller(Controller 和 RequestMapping 注解说明&#…...

【Go】常见的四个内存泄漏问题
Goroutine没有顺利结束 1、这里更多的是由于channelforselect导致的,错误的写法导致了发送者或接收者没有发现channel已经关闭,任务已经结束了,却仍然在尝试输入输出https://geektutu.com/post/hpg-exit-goroutine.html Map的remove方法不会…...
【LeetCode-简单】剑指 Offer 29. 顺时针打印矩阵(详解)
题目 输入一个矩阵,按照从外向里以顺时针的顺序依次打印出每一个数字。 示例 1: 输入:matrix [[1,2,3],[4,5,6],[7,8,9]] 输出:[1,2,3,6,9,8,7,4,5]示例 2: 输入:matrix [[1,2,3,4],[5,6,7,8],[9,10,1…...

TOMCAT基础
tomcat是一个基于Java开发的,开放源代码的web应用服务器。它可以解析html页面中的java代码,执行动态请求,实现动态页面。核心功能是将收到的http请求处理并转发给适当的servlet来处理,然后将响应返回给客户端。 优点 1,…...

自动化集装箱码头建设指南
1 总则 1.0.1 为规范和指导自动化集装箱码头建设,提高自动化集装箱码头建设和装卸自动化应用水平,做到技术先进、经济合理、安全可靠、高效节能、绿色环保,制定本指南。 1.0.2本指南适用于新建、改建和扩建自动化集装箱码头的设计࿰…...

为什么要用redis
高性能 就是把你一些复杂操作耗时查出来的结果(用了600ms),如果确定后面不咋变了,然后但是马上还有很多读请求,那么直接结果放缓存(6ms),后面直接读缓存就好了。 这样,性能就提升了100倍 高并发 说白了就是…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

土建施工员考试:建筑施工技术重点知识有哪些?
《管理实务》是土建施工员考试中侧重实操应用与管理能力的科目,核心考查施工组织、质量安全、进度成本等现场管理要点。以下是结合考试大纲与高频考点整理的重点内容,附学习方向和应试技巧: 一、施工组织与进度管理 核心目标: 规…...

rm视觉学习1-自瞄部分
首先先感谢中南大学的开源,提供了很全面的思路,减少了很多基础性的开发研究 我看的阅读的是中南大学FYT战队开源视觉代码 链接:https://github.com/CSU-FYT-Vision/FYT2024_vision.git 1.框架: 代码框架结构:readme有…...
Android屏幕刷新率与FPS(Frames Per Second) 120hz
Android屏幕刷新率与FPS(Frames Per Second) 120hz 屏幕刷新率是屏幕每秒钟刷新显示内容的次数,单位是赫兹(Hz)。 60Hz 屏幕:每秒刷新 60 次,每次刷新间隔约 16.67ms 90Hz 屏幕:每秒刷新 90 次,…...

【笔记】AI Agent 项目 SUNA 部署 之 Docker 构建记录
#工作记录 构建过程记录 Microsoft Windows [Version 10.0.27871.1000] (c) Microsoft Corporation. All rights reserved.(suna-py3.12) F:\PythonProjects\suna>python setup.py --admin███████╗██╗ ██╗███╗ ██╗ █████╗ ██╔════╝…...