JVM---垃圾回收算法介绍
目录
分代收集理论
三种垃圾回收算法
标记-清除算法(最基础的、基本不用)
标记-复制算法
标记-整理算法
正式因为jvm有了垃圾回收机制,作为java开发者不会去特备关注内存,不像C和C++。
优点:开发门槛低、安全
缺点:性能问题。c和c++可以自己操控内存等,性能更高
垃圾回收学的是算法,垃圾回收有很多种算法,学完这个的目标一个是需要学习人家的思路,第二个是需要根据自己的业务特色去选用特定的垃圾回收算法
分代收集理论
建立在两个假说之上:
弱分代假说(Weak Generational Hypothesis):绝大多数对象都是朝生夕灭的。
强分代假说(Strong Generational Hypothesis):熬过越多次垃圾收集过程的对象就越难以消亡。
原理:收集器应该将Java堆划分出不同的区域,然后将回收对象依据其年龄(年龄即对象熬过垃圾收集过程的次数)分配到不同的区域之中存储。根据不同区域采取不同的垃圾回收算法。至少将java堆分为两部分:新生代和老年代。新生代中存朝生夕灭的对象,老年代中存熬过很多次垃圾回收。新生代熬过一次加一,到特定数值移到老年代中。
分代的好处:时间开销、内存空间的有效利用
分代的弊端:如果新生代中的对象被老年代中引用,则在每次回收需要扫描所有老年代检查饮用者是否是否存活,即跨界引用的问题。
分代弊端的解决方法:为了解决跨代引用,增加第三条法则:跨代引用相对同代引用更容易存活,很容易成为老年代对象,进而成为同代引用。同时为了不扫描整个老年代,老年代开辟出一块空间,这块空间只放跨代引用的对象
三种垃圾回收算法
标记-清除算法(最基础的、基本不用)
原理:标记哪些对象存活那些死亡,然后清除死亡的
弊端:
①、效率问题:如果Java堆中包含大量对象,而且其中大部分是需要被回收的,这时必须进行大量标记和清除的动作,导致标记和清除两个过程的执行效率都随对象数量增长而降低
②、内存碎片问题:之后可能因为没有足够的空间放大文件而导致下一次的垃圾回收提前
标记-复制算法
原理:空间分为1:1,在用的时候用一半,垃圾清除的时候将所用一半中不需要清除的顺序地放到另一半上。研究表明,百分之98的对象熬不过第一轮垃圾清除,所以不需要1:1。将jvm堆区域分为三份(80%、10%10%),每次新生代可用的内存空间为其中的两份占90%,而将其中不需要清理的放到剩余的百分之十上面,再次使用时空间为80%和这百分之10
解决了效率问题和内存碎片的问题
标记-整理算法
产生原因:标记复制中对象存活率较高时需要进行较多的复制操作,效率低。
原理:先标记,将存活的对象移动到一端,然后设置边界,另外一端全删。解决了碎片化的问题,
弊端:如果每次回收有大量存活,移动和更新耗费大量资源。在标记的时候需要停下所有的应用程序,不然可能标记完之后再次更改空间大小,使得标记的数据不准确。内存的访问是用户程序中最频繁的操作之一,假如宕机的话,会直接影响应用程序的运行
解决方法:在平时进行标记清除,碎片化程度影响内存分配时进行标记整理
注:通常标记-清除算法也是需要停顿用户线程来标记、清理可回收对象的,只是停顿时间相对而言要来的短而已。
相关文章:

JVM---垃圾回收算法介绍
目录 分代收集理论 三种垃圾回收算法 标记-清除算法(最基础的、基本不用) 标记-复制算法 标记-整理算法 正式因为jvm有了垃圾回收机制,作为java开发者不会去特备关注内存,不像C和C。 优点:开发门槛低、安全 缺点…...
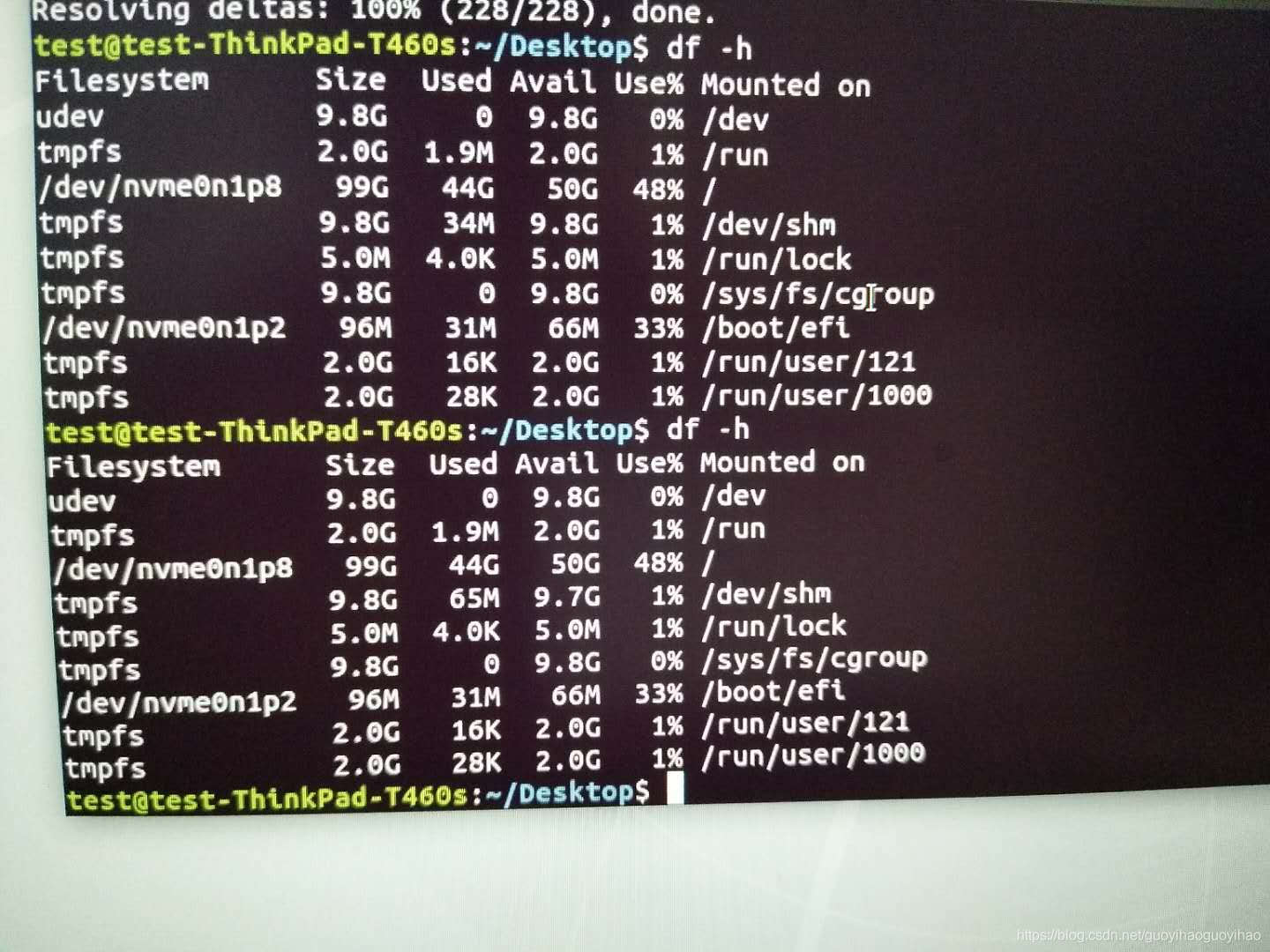
Ubuntu一直卡死的问题(20.04)
Ubuntu一直卡死的问题(18.04)_ubuntu频繁死机_Mr.Yi的博客-CSDN博客 我自己的解决方法: 1、首先强制关机重启后,直接打开命令行查看磁盘的使用: df -h发现/dev/loop都沾满了,我们能需要做的就是把他们清理干净 sud…...

自动化测试用例设计实例
在编写用例之间,笔者再次强调几点编写自动化测试用例的原则: 1、一个脚本是一个完整的场景,从用户登陆操作到用户退出系统关闭浏览器。 2、一个脚本脚本只验证一个功能点,不要试图用户登陆系统后把所有的功能都进行验证再退出系统…...
CSS3基础
CSS3在CSS2的基础上增加了很多功能,如圆角、多背景、透明度、阴影等,以帮助开发人员解决一些实际问题。 1、初次使用CSS 与HTML5一样,CSS3也是一种标识语言,可以使用任意文本编辑器编写代码。下面简单介绍CSS3的基本用法。 1.1…...

【栈】 735. 行星碰撞
735. 行星碰撞 解题思路 如果数组元素大于0 说明向右移动 那么不管 左边元素是不是大于0 都不会碰撞 如果数组元素小于0 说明想左边移动 那么判断左边元素 如果左边元素大于0 碰撞 那么遍历数组 当前元素大于0 直接入栈 如果当前元素小于0 判断栈顶元素是不是大于0 如果大…...
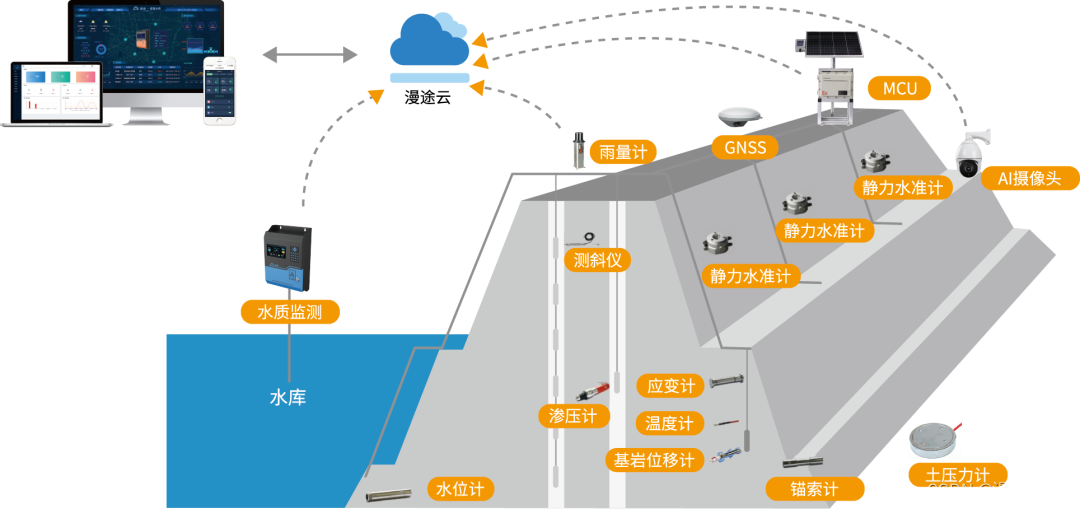
水库大坝安全监测MCU,提升大坝管理效率的利器!
水库大坝作为防洪度汛的重要设施,承担着防洪抗旱,节流发电的重要作用。大坝的安全直接关系到水库的安全和人民群众的生命财产安全。但因为水库大坝的隐患不易被察觉,发现时往往为时已晚。因此,必须加强对大坝的安全管理。其安全监…...

【vue2类型助手】vue2-cli 实现为 vue2 项目中的组件添加全局类型提示
实现 vue2 全局组件提示 vue2 项目全局注册组件直接使用没有提示 由于vue2中使用volar存在很大的性能问题,所以只能继续使用vetur,但是这样全局组件会没有提示,这对于开发来说,体验十分不友好,所以开发此cli并借助ve…...

mysql 索引 区分字符大小写
mysql 建立索引,特别是unique索引,是跟字符集、字符排序规则有关的。 对于utf8mb4_0900_ai_ci来说,0900代表Unicode 9.0的规范,ai表示accent insensitivity,也就是“不区分音调”,而ci表示case insensitiv…...

Stable Diffusion Webui源码剖析
1、关键python依赖 (1)xformers:优化加速方案。它可以对模型进行适当的优化来加速图片生成并降低显存占用。缺点是输出图像不稳定,有可能比不开Xformers略差。 (2)GFPGAN:它是腾讯开源的人脸修…...

为什么kafka 需要 subscribe 的 group.id?我们是否需要使用 commitSync 手动提交偏移量?
目录 一、为什么需要带有 subscribe 的 group.id二、我们需要使用commitSync手动提交偏移量吗?三、如果我想手动提交偏移量,该怎么做? 一、为什么需要带有 subscribe 的 group.id 消费概念: Kafka 使用消费者组的概念来实现主题的…...

什么是Web应用程序防火墙,WAF与其他网络安全工具差异在哪?
一、什么是Web 应用程序防火墙 (WAF) ? WAF软件产品被广泛应用于保护Web应用程序和网站免受威胁或攻击,它通过监控用户、应用程序和其他互联网来源之间的流量,有效防御跨站点伪造、跨站点脚本(XSS攻击)、SQL注入、DDo…...

打家劫舍 II——力扣213
动规 int robrange(vector<int>& nums, int start, int end){int first=nums[start]...
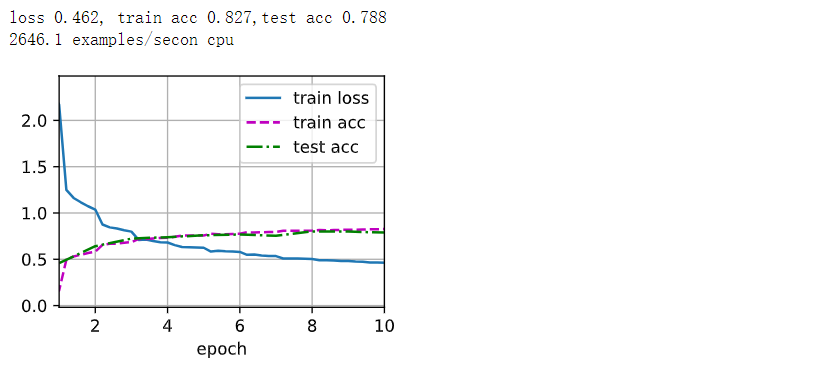
动手学深度学习—卷积神经网络LeNet(代码详解)
1. LeNet LeNet由两个部分组成: 卷积编码器:由两个卷积层组成;全连接层密集块:由三个全连接层组成。 每个卷积块中的基本单元是一个卷积层、一个sigmoid激活函数和平均汇聚层;每个卷积层使用55卷积核和一个sigmoid激…...

腾讯面经总结
最近在准备面试,看了很多大厂的面经,抽空将腾讯面试的题目整理了一下,希望对大家有所帮助~ 一面 1、mysql索引结构? 2、redis持久化策略? 3、zookeeper节点类型说一下; 4、zookeeper选举机制ÿ…...

matlab机器人工具箱基础使用
资料:https://blog.csdn.net/huangjunsheng123/article/details/110630665 用vscode直接看工具箱api代码比较方便,代码说明很多 一、模型设置 1、基础效果 %采用机器人工具箱进行正逆运动学验证 a[0,-0.3,-0.3,0,0,0];%DH参数 d[0.05,0,0,0.06,0.05,…...

利用WonderLeak进行内存泄露检测【一】
1、下载地址: WonderLeak - Visual Studio Marketplace https://www.relyze.com/ 2、WonderLeak支持vs2017 2019扩展,或者单独启动 3、https://www.relyze.com/docs/wonderleak/help/w/overview/msvc_extension1.png 4、对于二进制程序来说支持以下…...
,思维题)
二刷LeetCode--155. 最小栈(C++版本),思维题
思路:本题需要使用两个栈,一个就是正常栈,执行出入操作,另一个栈只负责将对应的最小值进行保存即可.每次入栈的时候,最小值栈的栈顶也需要入栈元素,不过这个元素是最小值,那么就需要进行比较,因此在getmin()的时候只需要将最小值栈的栈顶元素弹出即可.初始化的时候只需要将最小…...

进程的状态与转换
进程在其生命周期内,由于系统中各进程之间的相互制约及系统的运行环境的变化,使得进程的状态也在不断地发生变化。通常进程有以下5种状态,前三种是基础讷航的基本状态 1)运行态。进程正在处理机上运行。在单处理机机中࿰…...

用MariaDB创建数据库,SQL练习,MarialDB安装和使用
前言:MariaDB数据库管理系统是MySQL的一个分支,主要由开源社区在维护,采用GPL授权许可 MariaDB的目的是完全兼容MySQL,包括API和命令行,使之能轻松成为MySQL的代替品。在存储引擎方面,使用XtraDB来代替MySQ…...

【Docker】 使用Docker-Compose 搭建基于 WordPress 的博客网站
引 本文将使用流行的博客搭建工具 WordPress 搭建一个私人博客站点。部署过程中使用到了 Docker 、MySQL 。站点搭建完成后经行了发布文章的体验。 WordPress WordPress 是一个广泛使用的开源内容管理系统(CMS),用于构建和管理网站、博客和…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...

数据结构:递归的种类(Types of Recursion)
目录 尾递归(Tail Recursion) 什么是 Loop(循环)? 复杂度分析 头递归(Head Recursion) 树形递归(Tree Recursion) 线性递归(Linear Recursion)…...

二维FDTD算法仿真
二维FDTD算法仿真,并带完全匹配层,输入波形为高斯波、平面波 FDTD_二维/FDTD.zip , 6075 FDTD_二维/FDTD_31.m , 1029 FDTD_二维/FDTD_32.m , 2806 FDTD_二维/FDTD_33.m , 3782 FDTD_二维/FDTD_34.m , 4182 FDTD_二维/FDTD_35.m , 4793...
