机器学习:隐马尔可夫模型(HMM)
后续会回来补充代码
1 隐马尔可夫模型
隐马尔可夫模型(Hidden Markov Model,HMM)是可用于标注问题的统计学模型,描述由隐藏的马尔可夫链随机生成观测序列的过程。
1.1 数学定义
隐马尔可夫模型是关于时序的概率模型,描述由一个隐藏的马尔可夫链随机生成不可观测的状态随机序列,再由各个状态生成同一个观测从而产生观测随机序列的过程。隐藏的马尔可夫链随机生成状态序列,而每一个状态又生成一个观测。序列的每一个位置称作一个时刻。
隐马尔可夫模型可以由初始状态概率向量 π \pi π,状态转移矩阵 A A A和观测矩阵 B B B决定。 π \pi π和 A A A决定状态序列, B B B决定观测序列。隐马尔可夫模型可以记作: λ = ( π , A , B ) \lambda=(\pi,A,B) λ=(π,A,B)。其各个部分的介绍如下:
记 Q = { q 1 , q 2 , … , q N } Q=\{q_{1},q_{2},\dots,q_{N}\} Q={q1,q2,…,qN}为所有可能的状态集合, V = { v 1 , v 2 , … , v M } V=\{v_{1}, v_{2},\dots,v_{M}\} V={v1,v2,…,vM}为所有可能的观测集合。假设目前得到的 T T T个时刻观测序列 O = ( o 1 , o 2 , … , o T ) O=(o_{1},o_{2},\dots,o_{T}) O=(o1,o2,…,oT),其对应的状态序列记为 I = ( i 1 , i 2 , … , i T ) I=(i_{1},i_{2},\dots,i_{T}) I=(i1,i2,…,iT)。状态序列是不可知的
状态转移矩阵 A = [ a i j ] N × N A=[a_{ij}]_{N\times N} A=[aij]N×N, 其中 a i j = P ( i t + 1 = q j ∣ i t = q i ) , i , j = 1 , 2 , … , N a_{ij}=P(i_{t+1}=q_{j}|i_{t}=q_{i}),i,j=1,2,\dots,N aij=P(it+1=qj∣it=qi),i,j=1,2,…,N,即为在时刻 t t t处于状态 q i q_{i} qi的条件下在时刻 t + 1 t+1 t+1转移到状态 q j q_{j} qj的概率。观测矩阵 B = [ b j ( k ) ] N × M B=[b_{j}(k)]_{N\times M} B=[bj(k)]N×M,其中 b j ( k ) = P ( o t = v k ∣ i t = q j ) , k = 1 , 2 , … , M , j = 1 , 2 , … , N b_{j}(k)=P(o_{t}=v_{k}|i_{t}=q_{j}),k=1,2,\dots,M,j=1,2,\dots,N bj(k)=P(ot=vk∣it=qj),k=1,2,…,M,j=1,2,…,N为时刻 t t t处于状态 q j q_{j} qj的条件下生成观测 v k v_{k} vk的概率。
初始状态变量 π = ( π i ) \pi=(\pi_{i}) π=(πi),其中 π i = P ( i 1 = q i ) , i = 1 , 2 , … , N \pi_{i}=P(i_{1}=q_{i}),i=1,2,\dots,N πi=P(i1=qi),i=1,2,…,N为初始时刻 t = 1 t=1 t=1处于状态 q i q_{i} qi的概率。
1.2 基本假设
- 齐次马尔可夫假设:隐藏的马尔科夫链在任意时刻 t t t的状态只依赖于其前一个时刻状态,与其他时刻的状态和观测无关,也与时刻 t t t无关: P ( i t ∣ i t − 1 , o t − 1 , … , i 1 , o 1 ) = P ( i t ∣ i t − 1 ) , t = 1 , 2 , … , T P(i_{t}|i_{t-1},o_{t-1},\dots,i_{1},o_{1})=P(i_{t}|i_{t-1}),t=1,2,\dots,T P(it∣it−1,ot−1,…,i1,o1)=P(it∣it−1),t=1,2,…,T
- 观测独立性假设:任意时刻的观测只依赖于该时刻的马尔可夫链的状态,与其他观测及状态无关。
1.3 基本问题
- 概率计算问题:给定模型 λ = ( π , A , B ) \lambda=(\pi,A,B) λ=(π,A,B)和观测序列 O O O,计算该观测序列出现的概率 P ( O ∣ λ ) P(O|\lambda) P(O∣λ)。求解该问题可以使用前向算法和后向算法,这里不详细介绍。
- 学习问题:已知观测序列 O O O,估计模型 λ = ( π , A , B ) \lambda=(\pi,A,B) λ=(π,A,B)参数,使得在该模型下观测序列概率 P ( O ∣ λ ) P(O|\lambda) P(O∣λ)最大。求解该问题主要使用Baum-Welch算法(这个算法是EM算法的一种特例,EM算法在三硬币模型上的推导过程参考:https://blog.csdn.net/yeshang_lady/article/details/132151771)。这里不再赘述。
- 预测问题:又被称为解码问题。已知模型 λ = ( π , A , B ) \lambda=(\pi,A,B) λ=(π,A,B)和观测序列 O O O,求对给定观测序列条件概率 P ( I ∣ O ) P(I|O) P(I∣O)最大的状态序列。这里主要介绍维特比算法。
2 预测问题
2.1 维特比算法
维特比算法是一个动态规划算法,其规划过程与前向算法类似。两个算法的区别在于:评估问题的前向算法会保留每一条路径的概率,最终结果是各概率之和;维特比算法是计算给定观测序列下最可能的隐藏状态序列,因此每一步都只保留概率最大的路径,最终结果是一条概率最大的路径。其算法流程如下:
输入: 模型 λ = ( A , B , π ) \lambda=(A,B,\pi) λ=(A,B,π)和观测序列 O = ( o 1 , o 2 , … , o T ) O=(o_{1},o_{2},\dots,o_{T}) O=(o1,o2,…,oT);
输出:最优路径 I ∗ = ( i 1 ∗ , i 2 ∗ , … , i T ∗ ) I^{*}=(i_{1}^{*},i_{2}^{*},\dots,i_{T}^{*}) I∗=(i1∗,i2∗,…,iT∗)。
步骤: (1)初始化 δ 1 ( i ) = π i b i ( o 1 ) , i = 1 , 2 , … , N \delta_{1}(i)=\pi_{i}b_{i}(o_{1}),i=1,2,\dots,N δ1(i)=πibi(o1),i=1,2,…,N Ψ 1 ( i ) = 0 , i = 1 , 2 , … , N \Psi_{1}(i)=0,i=1,2,\dots,N Ψ1(i)=0,i=1,2,…,N(2)递推。对 t = 2 , 3 , … , T t=2,3,\dots,T t=2,3,…,T δ t ( i ) = m a x 1 ≤ j ≤ N [ δ t − 1 ( j ) a j i ] b i ( o t ) , i = 1 , 2 , … , N \delta_{t}(i)=\underset {1\le j\le N}{max}[\delta_{t-1}(j)a_{ji}]b_{i}(o_{t}),i=1,2,\dots,N δt(i)=1≤j≤Nmax[δt−1(j)aji]bi(ot),i=1,2,…,N Ψ t ( i ) = a r g m a x 1 ≤ j ≤ N [ δ t − 1 ( j ) a j i ] b i ( o t ) , i = 1 , 2 , … , N \Psi_{t}(i)=arg \underset {1\le j \le N}{max}[\delta_{t-1}(j)a_{ji}]b_{i}(o_{t}),i=1,2,\dots,N Ψt(i)=arg1≤j≤Nmax[δt−1(j)aji]bi(ot),i=1,2,…,N(3)终止 P ∗ = m a x 1 ≤ j ≤ N δ T ( i ) P^{*}=\underset {1\le j\le N}{max}\delta_{T}(i) P∗=1≤j≤NmaxδT(i) i T ∗ = a r g m a x 1 ≤ j ≤ N [ δ T ( i ) ] i^{*}_{T}=arg \underset {1\le j\le N}{max} [\delta_{T}(i)] iT∗=arg1≤j≤Nmax[δT(i)](4)最优路径回溯。对 t = T − 1 , T − 2 , … , 1 t=T-1,T-2,\dots,1 t=T−1,T−2,…,1 i t ∗ = Ψ t + 1 ( i t + 1 ∗ ) i^{*}_{t}=\Psi_{t+1}(i^{*}_{t+1}) it∗=Ψt+1(it+1∗)求得最优路径 I ∗ = ( i 1 ∗ , i 2 ∗ , … , i T ∗ ) I^{*}=(i_{1}^{*},i_{2}^{*},\dots,i_{T}^{*}) I∗=(i1∗,i2∗,…,iT∗)
参考资料
- 《统计学习方法》
相关文章:
)
机器学习:隐马尔可夫模型(HMM)
后续会回来补充代码 1 隐马尔可夫模型 隐马尔可夫模型(Hidden Markov Model,HMM)是可用于标注问题的统计学模型,描述由隐藏的马尔可夫链随机生成观测序列的过程。 1.1 数学定义 隐马尔可夫模型是关于时序的概率模型,描述由一个隐藏的马尔可夫链随机生成…...

使用插件实现pdf,word预览功能
效果 代码: 插件地址: https://github.com/501351981/vue-office <a-modalv-model:visible"visible":title"title"ok"handleOk":bodyStyle"bodyStyle":width"1200":maskClosable"false"…...
)
yolov5模型构建源码详细解读(yaml、parse_model等内容)
文章目录 前言一、yolov5文件说明二、yolov5调用模型构建位置三、模型yaml文件解析1、 yaml的backbone解读Conv模块参数解读C3模块参数解读 2、yaml的head解读Concat模块参数解读Detect模块参数解读 四、模型构建整体解读五、构建模型parse_model源码解读 前言 本文章记录yolo…...

Monodepth2和Lite-Mono准备数据集
以KITTI为例下载解压后放在/home/lwd/tmp/2011_09_26 cd /home/lwd/tmp/2011_09_26 ls输出 2011_09_26_drive_0001_sync 2011_09_26_drive_0002_sync 2011_09_26_drive_0005_sync python txt.py txt.py import os, sysalos.listdir(.) al.sort() fopen(train.txt, w) for a in…...

ML-fairness-gym入门教学
1、ML-fairness-gym简介 ML-fairness-gym是一个探索机器学习系统长期影响的工具。可以用于评估机器学习系统的公平性和评估静态数据集上针对各种输入的误差度量的差异。开源网站:GitHub - google/ml-fairness-gym 2、安装ML-fairness-gym(Windows&…...

结构体指针变量的使用
1、结构体指针的引用 #include<iostream> using namespace std;struct Student {int num;char name[32]; }; int main() {struct Student stu {1,"张三"};struct Student* p &stu;system("pause"); return 0; } 2、通过结构体指针访问结构体…...

解决oracle的em访问提示“使用不受支持的协议。”的bug
1. 设置oracle唯一名称 执行emctl时需要设置一个唯一的名称 否则提示 “Environment variable ORACLE_UNQNAME not defined. Please set ORACLE_UNQNAME to database unique name. ”中文意思为“未定义环境变量ORACLE_UNQNAME。 请将ORACLE_UNQNAME设置为数据库唯一名称/服务…...
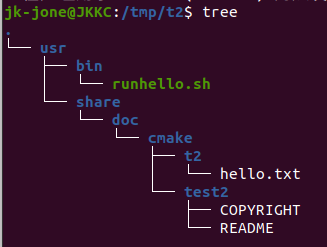
编译工具:CMake(三)| 最简单的实例升级
编译工具:CMake(三)| 最简单的实例升级 前言过程语法解释ADD_SUBDIRECTORY 指令 如何安装目标文件的安装普通文件的安装:非目标文件的可执行程序安装(比如脚本之类)目录的安装 修改 Helloworld 支持安装测试 前言 本篇博客的任务…...
常见系统库的使用)
20天学会rust(四)常见系统库的使用
前面已经学习了rust的基础知识,今天我们来学习rust强大的系统库,从此coding事半功倍。 集合 数组&可变长数组 在 Rust 中,有两种主要的数组类型:固定长度数组(Fixed-size Arrays)和可变长度数组&…...
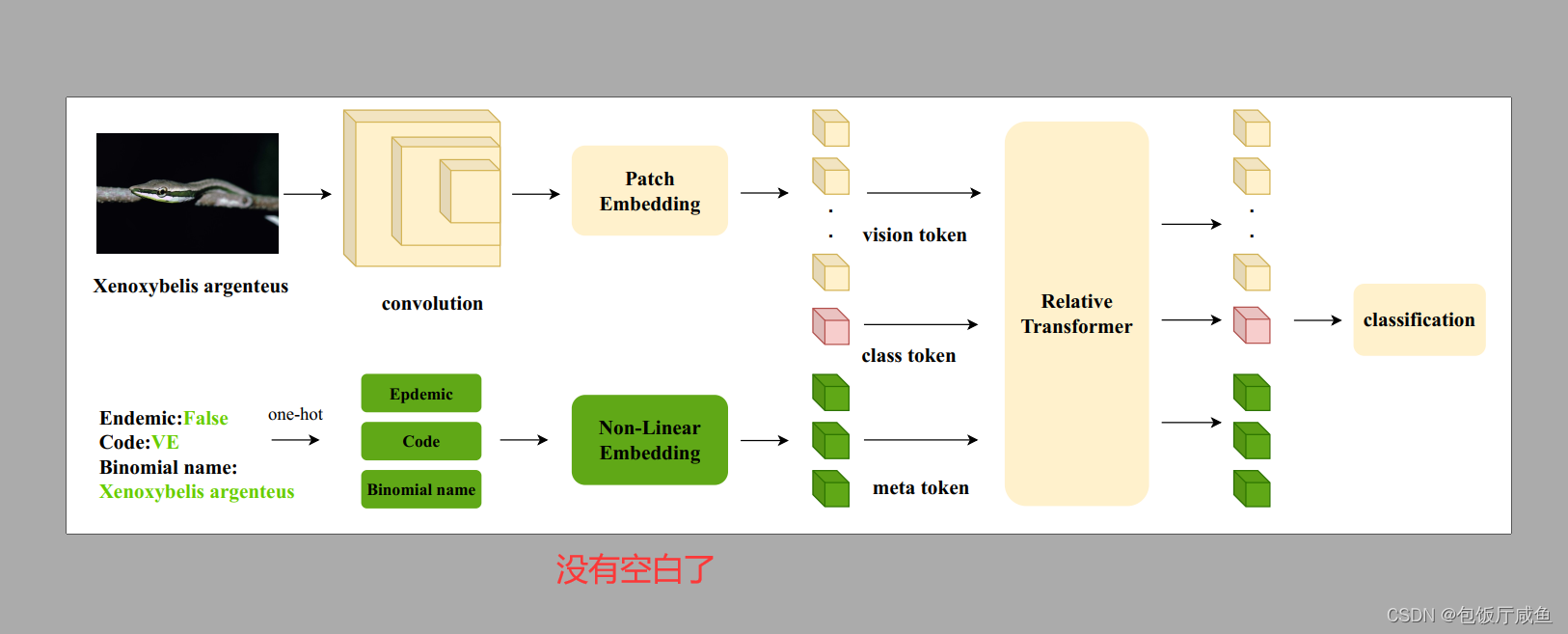
drawio----输出pdf为图片大小无空白(图片插入论文)
自己在写论文插入图片时为了让论文图片放大不模糊,啥方法都试了,最后摸索出来这个。 自己手动画图的时候导出pdf总会出现自己的图片很小,pdf的白边很大如下如所示,插入论文的时候后虽然放大不会模糊,但是白边很大会显…...

2021年09月 C/C++(二级)真题解析#中国电子学会#全国青少年软件编程等级考试
第1题:字符统计 给定一个由a-z这26个字符组成的字符串,统计其中哪个字符出现的次数最多。 输入 输入包含一行,一个字符串,长度不超过1000。 输出 输出一行,包括出现次数最多的字符和该字符出现的次数,中间以…...
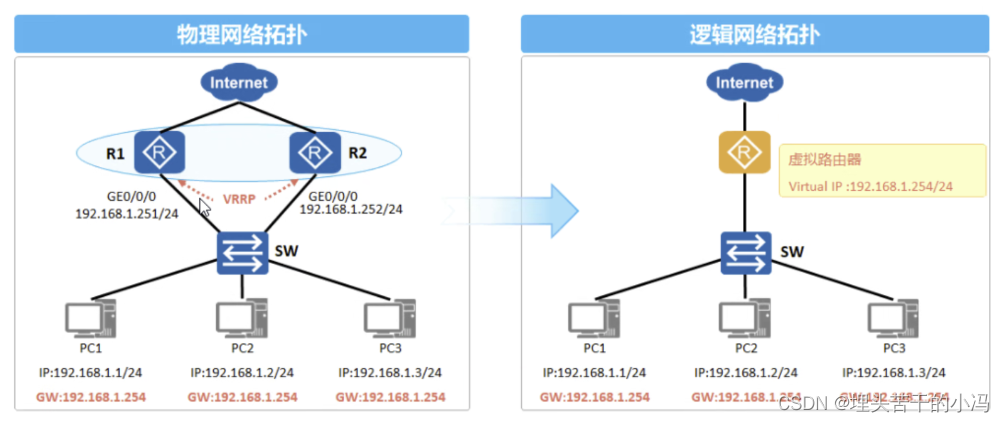
HCIP VRRP技术
一、VRRP概述 VRRP(Virtual Router Pedundancy Protocol)虚拟路由器冗余协议,既能够实现网关的备份,又能够解决多个网关之间互相冲突的问题,从而提高网络可靠性。 局域网中的用户的终端通常采用配置一个默认网关的形…...

JAVA AES ECB/CBC 加解密
JAVA AES ECB/CBC 加解密 1. AES ECB2. AES CBC 1. AES ECB package org.apache.jmeter.functions;/*** author yuyang*/import org.apache.commons.lang3.StringUtils; import java.util.Base64; import javax.crypto.Cipher; import javax.crypto.spec.SecretKeySpec;/*** a…...
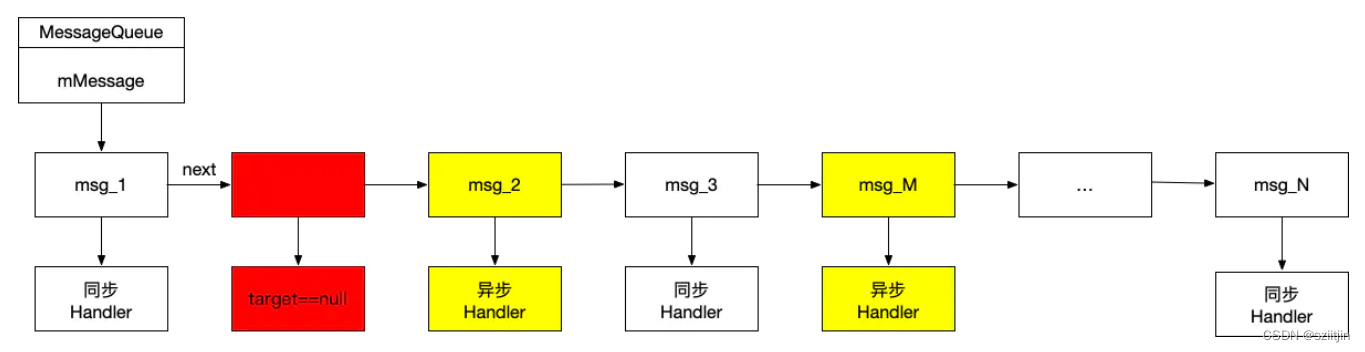
Android FrameWork 层 Handler源码解析
Handler生产者-消费者模型 在android开发中,经常会在子线程中进行一些耗时操作,当操作完毕后会通过handler发送一些数据给主线程,通知主线程做相应的操作。 其中:子线程、handler、主线程,其实构成了线程模型中经典的…...

list
目录 迭代器 介绍 种类 本质 介绍 模拟实现 注意点 代码 迭代器 介绍 在C中,迭代器(Iterators)是一种用于遍历容器(如数组、vector、list等)中元素的工具 无论容器的具体实现细节如何,访问容器中的元素的方…...

ABeam×Startup丨德硕管理咨询(深圳)创新研究团队前往灵境至维·既明科技进行拜访交流
近日,德硕管理咨询(深圳)(以下简称“ABeam-SZ”)创新研究团队一行前往灵境至维既明科技有限公司(以下简称“灵境至维”)进行拜访交流,探讨线上虚拟空间的商业模式。 现场合影 &…...

TCP的相关性质
文章目录 流量控制拥塞控制拥塞窗口 延迟应答捎带应答面向字节流粘包问题TCP的异常 流量控制 由于接收端处理数据的速度是有限的,如果发送端发的太快,那么接收端的缓冲区就可能会满。此时如果发送端还发数据,就会出现丢包现象,并…...

pointpillars在2D CNN引入自适应注意力机制
在给定的代码中,您想要引入自适应注意力机制。自适应注意力机制通常用于增强模型的感受野,从而帮助模型更好地捕捉特征之间的关系。在这里,我将展示如何在您的代码中引入自适应注意力机制,并提供详细的解释。 首先,让…...
【每日一题】1572. 矩阵对角线元素的和
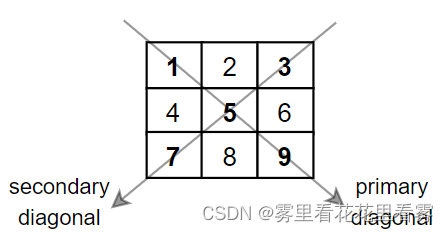
【每日一题】1572. 矩阵对角线元素的和 1572. 矩阵对角线元素的和题目描述解题思路 1572. 矩阵对角线元素的和 题目描述 给你一个正方形矩阵 mat,请你返回矩阵对角线元素的和。 请你返回在矩阵主对角线上的元素和副对角线上且不在主对角线上元素的和。 示例 1&a…...

leetcode原题:检查子树
题目: 检查子树。你有两棵非常大的二叉树:T1,有几万个节点;T2,有几万个节点。设计一个算法,判断 T2 是否为 T1 的子树。 如果 T1 有这么一个节点 n,其子树与 T2 一模一样,则 T2 为…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...
