二.net core 自动化发布到docker (Jenkins安装之后向导)
目录
参考资料:https://www.jenkins.io/doc/book/installing/docker/#setup-wizard
Post-installation setup wizard.(安装后安装向导)
基于上一篇文章安装,在安装并运行Jenkins(不包括使用Jenkins Operator安装)后,安装向导将在安装后启动。
解锁Jenkins
注:-可以忽略,上面已经获取到密码
使用插件定制Jenkins
创建第一个管理员用户
-
参考资料:https://www.jenkins.io/doc/book/installing/docker/#setup-wizard
-
Post-installation setup wizard.(安装后安装向导)
-
基于上一篇文章安装,在安装并运行Jenkins(不包括使用Jenkins Operator安装)后,安装向导将在安装后启动。
这个安装向导将引导您完成几个快速的“一次性”步骤,以解锁Jenkins,使用插件对其进行自定义,并创建第一个管理员用户,通过该用户您可以继续访问Jenkins。
解锁Jenkins
当您第一次访问一个新的Jenkins实例时,系统会要求您使用自动生成的密码将其解锁。
浏览至http://localhost:8080(或安装Jenkins时为其配置的任何端口)并等待直到出现Unlock Jenkins页面。

密码在:从Jenkins控制台日志输出中,复制自动生成的字母数字密码(在两组星号之间)。
docker logs id
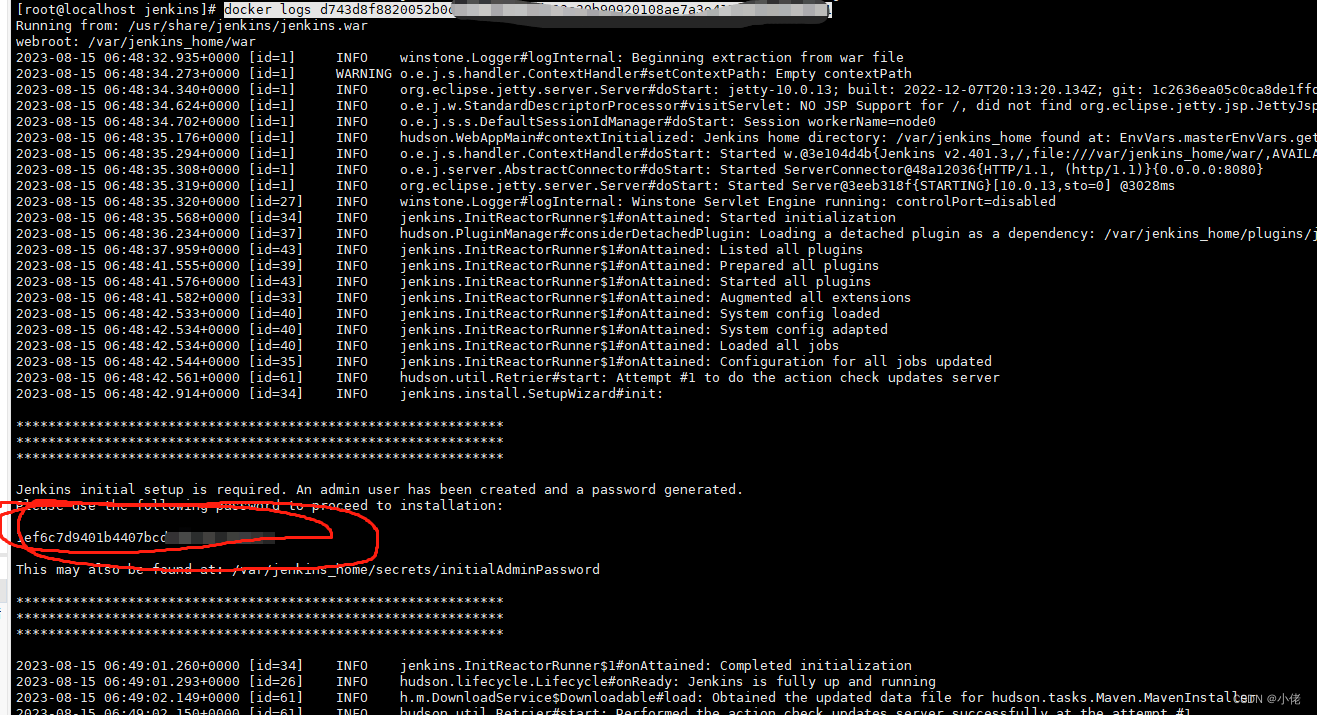
注:-可以忽略,上面已经获取到密码
sudo cat/var/lib/jenkins/secrets/initialAdminPassword命令将在控制台打印密码。
如果您使用正式的Jenkins/Jenkins映像在Docker中运行Jenkins,则可以使用sudo Docker exec${CONTAINER\u ID或CONTAINER\u NAME}cat/var/Jenkins\u home/secrets/initialAdminPassword在控制台中打印密码,而无需执行到容器中。
在Unlock Jenkins页面上,将此密码粘贴到Administrator password字段,然后单击Continue。
注:
Jenkins控制台日志指示也可以获取此密码的位置(在Jenkins主目录中)。必须在新Jenkins安装的安装向导中输入此密码,然后才能访问Jenkins的主UI。如果您碰巧跳过安装向导中的后续用户创建步骤,此密码还将用作默认管理员帐户的密码(用户名为“admin”)。
使用插件定制Jenkins
解锁Jenkins后,将显示自定义Jenkins页面。在这里,您可以安装任何数量的有用插件作为初始设置的一部分。
单击显示的两个选项之一:
安装推荐的插件-安装推荐的插件集,这些插件基于最常见的用例。
选择要安装的插件-选择最初要安装的插件集。当您第一次访问插件选择页面时,默认情况下会选择建议的插件。
如果您不确定需要什么插件,请选择安装建议的插件。您可以稍后通过Jenkins中的Manage Jenkins>plugins页面安装(或删除)其他Jenkins插件。
安装向导显示正在配置的Jenkins进程和正在安装的所选Jenkins插件集。此过程可能需要几分钟。
创建第一个管理员用户
最后,在使用插件定制Jenkins之后,Jenkins要求您创建第一个管理员用户。
出现“创建第一个管理员用户”页面时,请在相应字段中指定管理员用户的详细信息,然后单击“保存并完成”。
当Jenkins is ready页面出现时,单击Start using Jenkins。
注意事项:
这一页可能表明Jenkins几乎准备好了!相反,如果是,请单击“重新启动”。
如果页面在一分钟后未自动刷新,请使用web浏览器手动刷新页面。
如果需要,使用您刚刚创建的用户的凭据登录到Jenkins,就可以开始使用Jenkins了!
相关文章:

二.net core 自动化发布到docker (Jenkins安装之后向导)
目录 参考资料:https://www.jenkins.io/doc/book/installing/docker/#setup-wizard Post-installation setup wizard.(安装后安装向导) 基于上一篇文章安装,在安装并运行Jenkins(不包括使用Jenkins Opera…...

【设计模式——学习笔记】23种设计模式——解释器模式Interpreter(原理讲解+应用场景介绍+案例介绍+Java代码实现)
案例引入 通过解释器模式来实现四则运算,如计算ab-c的值,具体要求 先输入表达式的形式,比如abc-de,要求表达式的字母不能重复在分别输入a,b,c,d,e的值最后求出结果 传统方案 编写一个方法,接收表达式的形式…...
【计算机网络】——数据链路层
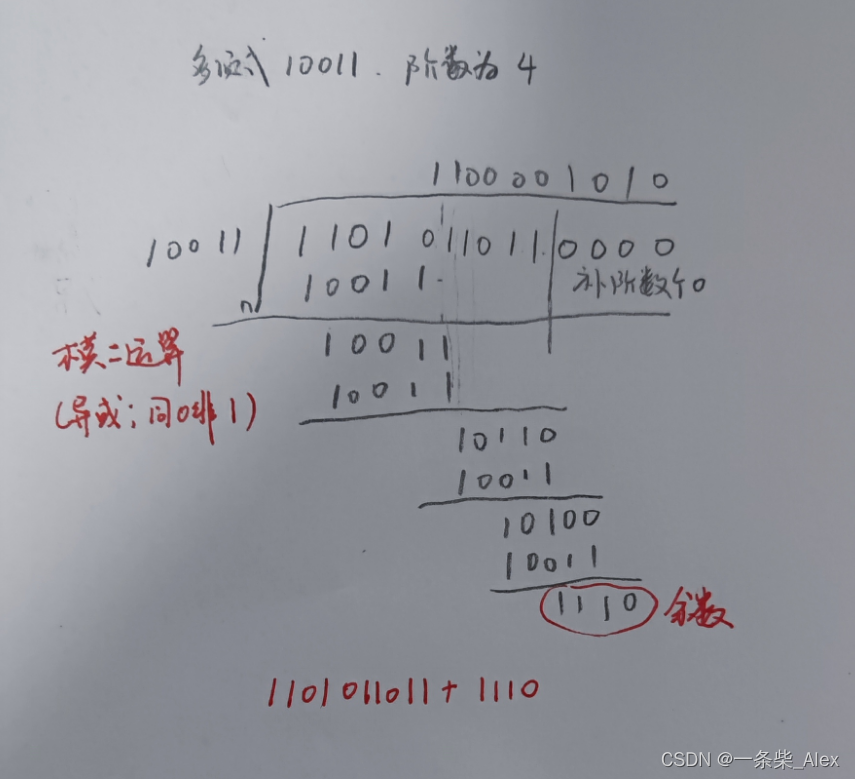
二、组帧 1、字符计数法 帧头部使用一个字符来表示帧的大小(包括第一个计数字符) (此处一字符一个字节) 2、字符填充收尾定界法 特定字符来定界帧的首和尾。若帧中数据段出现等同于特定字符的字符内容,前置一个转义字符。(类似于正则表达…...

数据结构:栈和队列(超详细)
目录 编辑 栈: 栈的概念及结构: 栈的实现: 队列: 队列的概念及结构: 队列的实现: 扩展知识: 以上就是个人学习线性表的个人见解和学习的解析,欢迎各位大佬在评论区探讨&#…...

AI项目二:基于mediapipe的虚拟鼠标控制
若该文为原创文章,转载请注明原文出处。 一、项目介绍 由于博主太懒,mediapipe如何实现鼠标控制的原理直接忽略,最初的想法是想控制摄像头识别手指控制鼠标,达到播放电影的效果。基本上效果也是可以的。简单的说是使用mediapipe检…...
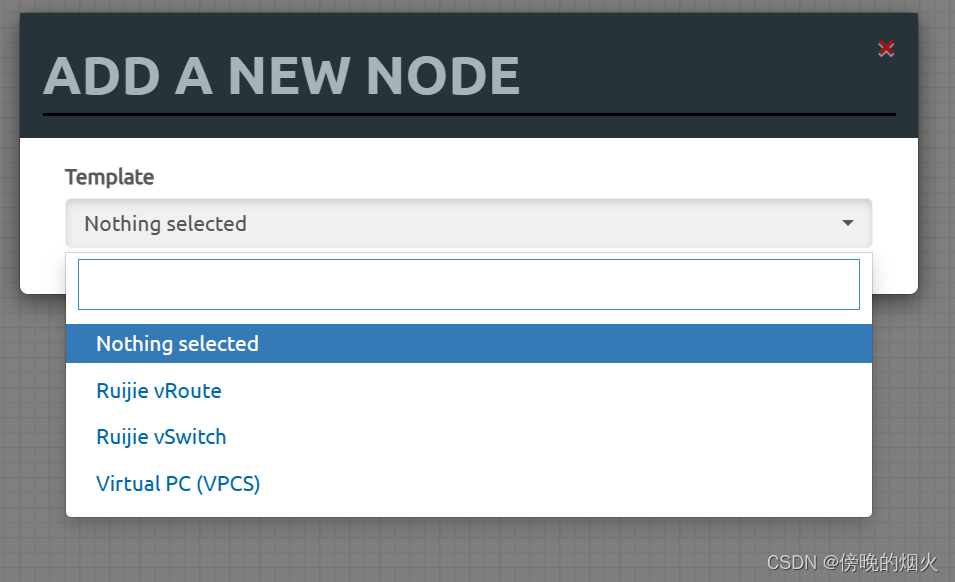
EVE-NG 隐藏没有镜像的模板
eve-ng 默认情况下,在添加node时,会列出所有的模板,这样用着很不方便。 通过以下方式,可以使没有设备的模板不可见 cp /opt/unetlab/html/includes/config.php.distribution /opt/unetlab/html/includes/config.php 打开 config…...

机器学习理论笔记(一):初识机器学习
文章目录 1 前言:蓝色是天的机器学习笔记专栏1.1 专栏初衷与定位1.2 本文主要内容 2 机器学习的定义2.1 机器学习的本质2.2 机器学习的分类 3 机器学习的基本术语4 探索"没有免费的午餐"定理(NFL)5 结语 1 前言:蓝色是天…...

Programming abstractions in C阅读笔记: p114-p117
《Programming Abstractions in C》学习第48天,p114-p117,总结如下: 一、技术总结 主要通过random number介绍了随机数的相关用法,interface示例(random.h),client program示例(craps.c)。 #include <stdio…...

分布式应用:Zabbix监控Tomcat
目录 一、理论 1.Zabbix监控Tomcat 二、实验 1.Zabbix监控Tomcat 三、问题 1.获取软件包失败 2.tomcat 配置 JMX remote monitor不生效 3.Zabbix客户端日志报错 一、理论 1.Zabbix监控Tomcat (1)环境 zabbix服务端:192.168.204.214 …...

《起风了》C++源代码
使用方法 Visual Studio、Dev-C、Visual Studio Code等C/C创建一个 .cpp 文件,直接粘贴赋值即可。 #include <iostream> #include <Windows.h> #pragma comment(lib,"winmm.lib") using namespace std; enum Scale {Rest 0, C8 108, B7 …...
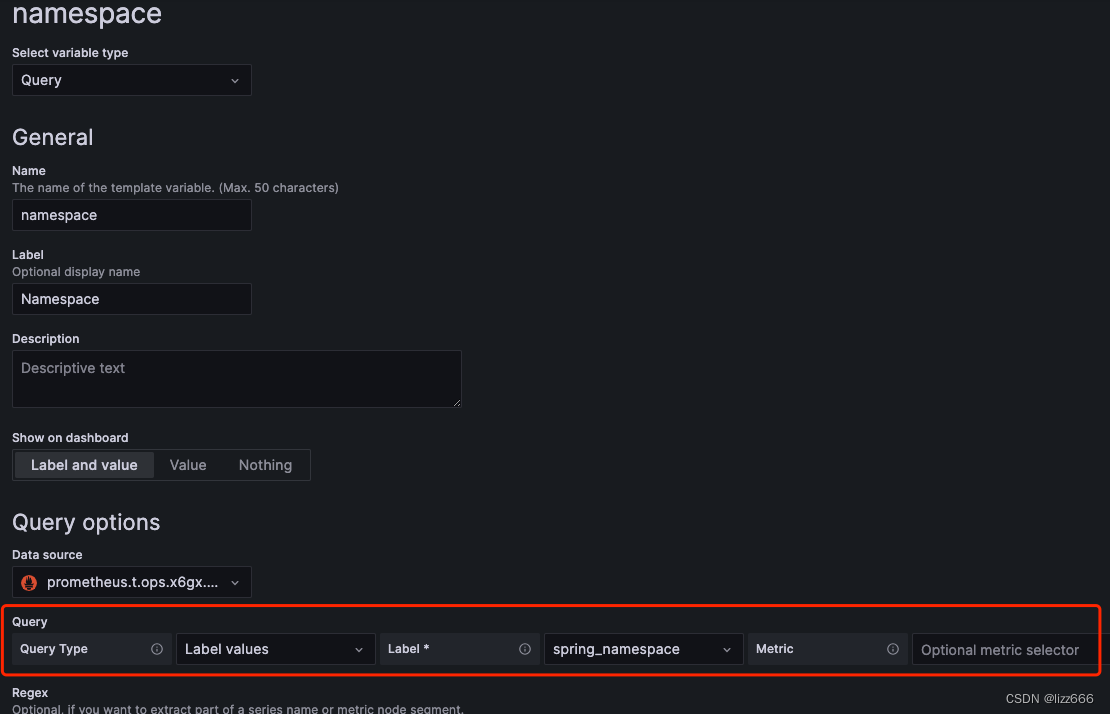
Grafana展示k8s中pod的jvm监控面板/actuator/prometheus
场景 为保障java服务正常运行,对服务的jvm进行监控,通过使用actuator组件监控jvm情况,使用prometheus对数据进行采集,并在Grafana展现。 基于k8s场景 prometheus数据收集 配置service的lable,便于prometheus使用labl…...
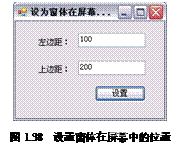
实例038 设置窗体在屏幕中的位置
实例说明 在窗体中可以设置窗体居中显示,本例通过设置窗体的Left属性和Top属性可以准确设置窗体的位置。运行本例,效果如图1.38所示。 技术要点 设置窗体在屏幕中的位置,可以通过设置窗体的属性来实现。窗体的Left属性表示窗体距屏幕左侧的…...

合成数据及其在AI领域中的作用
什么是合成数据? 合成数据是由人工创建而非从现实生活中获得的数据,它从机器学习对数据的需求发展而来。最初,为了精确训练AI模型,必须获得涵盖所有可能场景的训练数据。如果某个场景没有发生或未被获得,就没有相应的…...
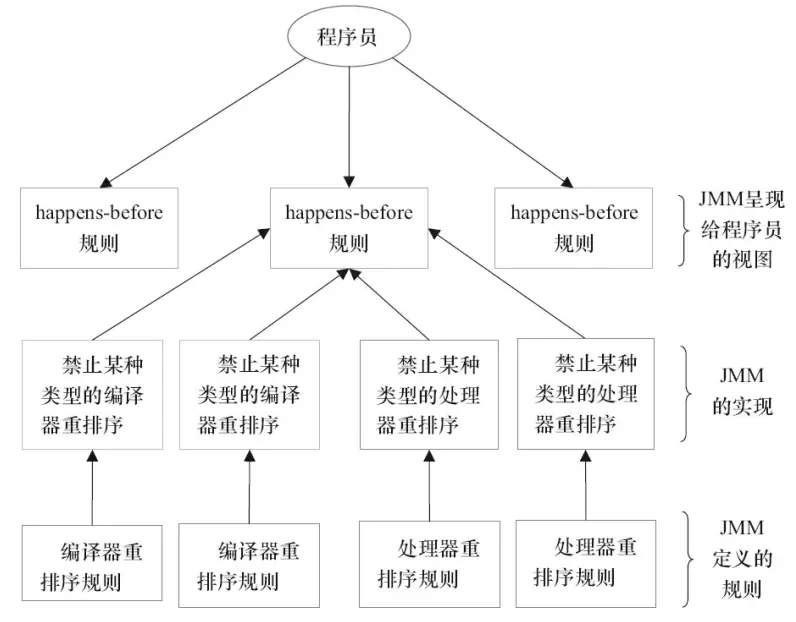
Java内存区域(运行时数据区域)和内存模型(JMM)
Java 内存区域和内存模型是不一样的东西,内存区域是指 Jvm 运行时将数据分区域存储,强调对内存空间的划分。 而内存模型(Java Memory Model,简称 JMM )是定义了线程和主内存之间的抽象关系,即 JMM 定义了 …...

【HDFS】hdfs的count命令的参数详解
Usage: hadoop fs -count [-q] [-h] [-v] [-x] [-t [<storage type>]] [-u] [-e] [-s] <paths...

Lombok注解在JSON化中,JSON生成额外生成字段问题
问题描述: 定义如下对象 Dataclass A{private String A;public String getC() {return "abab";}} 执行如下逻辑 Autowiredprivate ObjectMapper objectMapper;Testpublic void test4() throws Exception {A a new A();a.setA("a");System.ou…...
docker中的jenkins之流水线构建
docker中的jenkins之流水线构建项目 1、用node这种方式(因为我用pipeline方式一直不执行,不知道为什么) 2、创建项目 创建两个参数,一个是宿主端口号,一个是docker中的端口号 3、使用git项目中的Jenkinsfile 4、编写…...
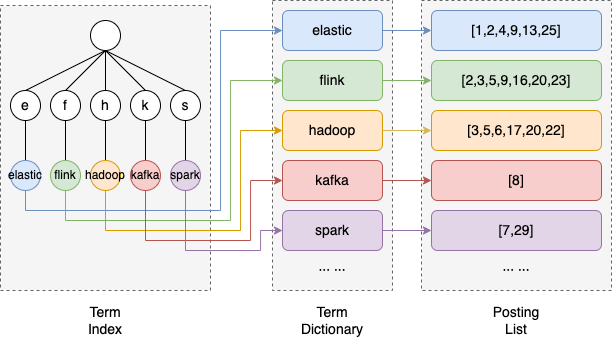
ES中倒排索引机制
在ES的倒排索引机制中有四个重要的名词:Term、Term Dictionary、Term Index、Posting List。 Term(词条):词条是索引里面最小的存储和查询单元。一段文本经过分析器分析以后就会输出一串词条。一般来说英文语境中词条是一个单词&a…...

一生一芯4——使用星火应用商店在ubuntu下载QQ、微信、百度网盘
星火应用商店可以非常方便的完成一些应用的下载,下面是官方网址 http://spark-app.store/download 我使用的是intel处理器,无需下载依赖项,直接点击软件本体 我这里下载amd64,根据自己的处理器下载对应版本 sudo apt install ./spark-stor…...
编程练习(1)
目录 一.选择题 第一题: 第二题: 第三题: 第四题: 第五题: 编辑 二.编程题 第一题: 第二题: 1.暴力方法: 2.数组法: 一.选择题 第一题: 解析&…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...
