【无人机路径规划】基于IRM和RRTstar进行无人机路径规划(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码、文章详细讲解
💥1 概述
本文将无人机路径规划这一非线性规划问题(NLP)转化为一般二次约束二次规划问题(QCQP),并使用IRM方法求解该QCQP问题。本文的方法不需要给定初值并且在保证线性收敛速率的情况下收敛到局部最小解,克服了NLP求解器和配点法(Collocation Method)初值难猜测和收敛到局部最小值速度很慢,甚至有时不能收敛到可行解的问题。
- 这里是列表文本引言
- 问题建模
- 数值优化法
3.1 运动规划问题转化为QCQP问题:采用数值微分的方法将问题离散化,消除约束中的三角函数,将NLP问题转化为非凸QCQP问题
3.2 使用IRM法求解一般QCQP问题- 启发式搜索法
4.1 RRT算法
4.2 改进的RRT算法- 仿真验证
- 结论
- 先使用传统RRTstar算法求解一条可行路径PP,Path_Opt()函数以PP为输入,从路径PP上随机采样不共线两点p1,p2p1,p2,如果p1,p2p1,p2连线不与障碍物冲突,用p1,p2p1,p2代替p1,p2p1,p2间的原本可行路径PP中的路径点,这样可以求出一条比路径PP短的路径。
- Steering_eval()函数判断路径是否满足方向角速率θ˙θ˙约束。路径上三个相邻点组成一个圆弧s,圆心角θθ除以通过该段圆弧所用时间tt近似等于θ˙
文献来源:

📚2 运行结果

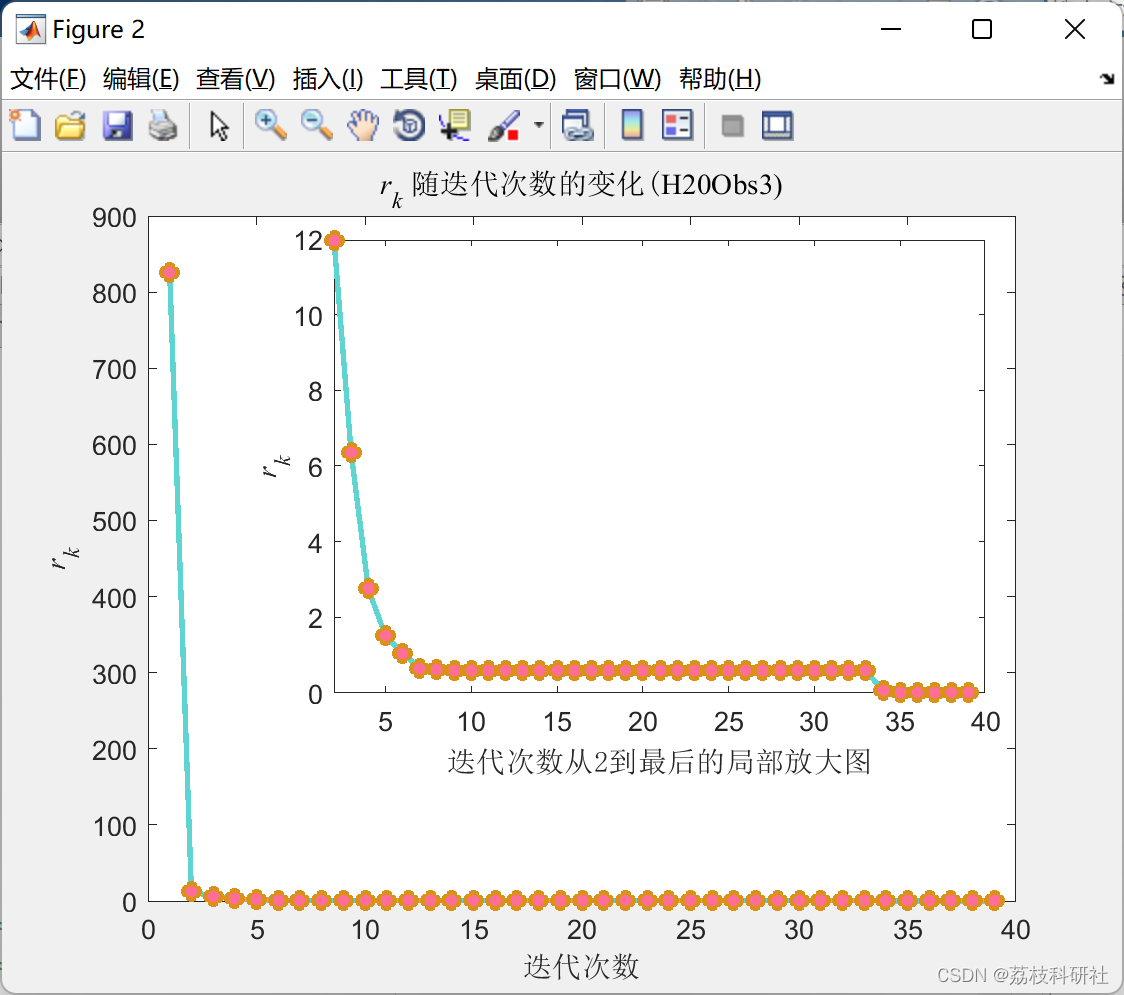
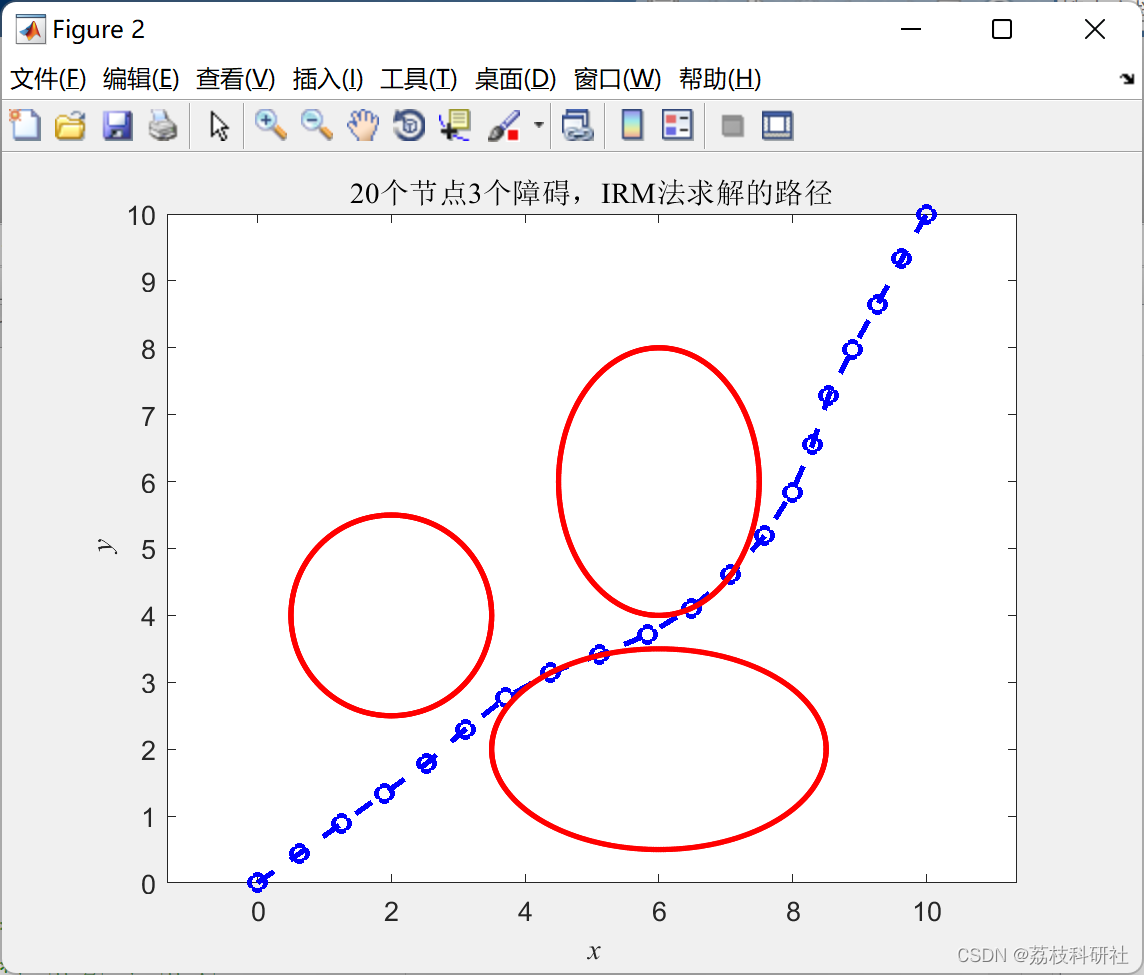

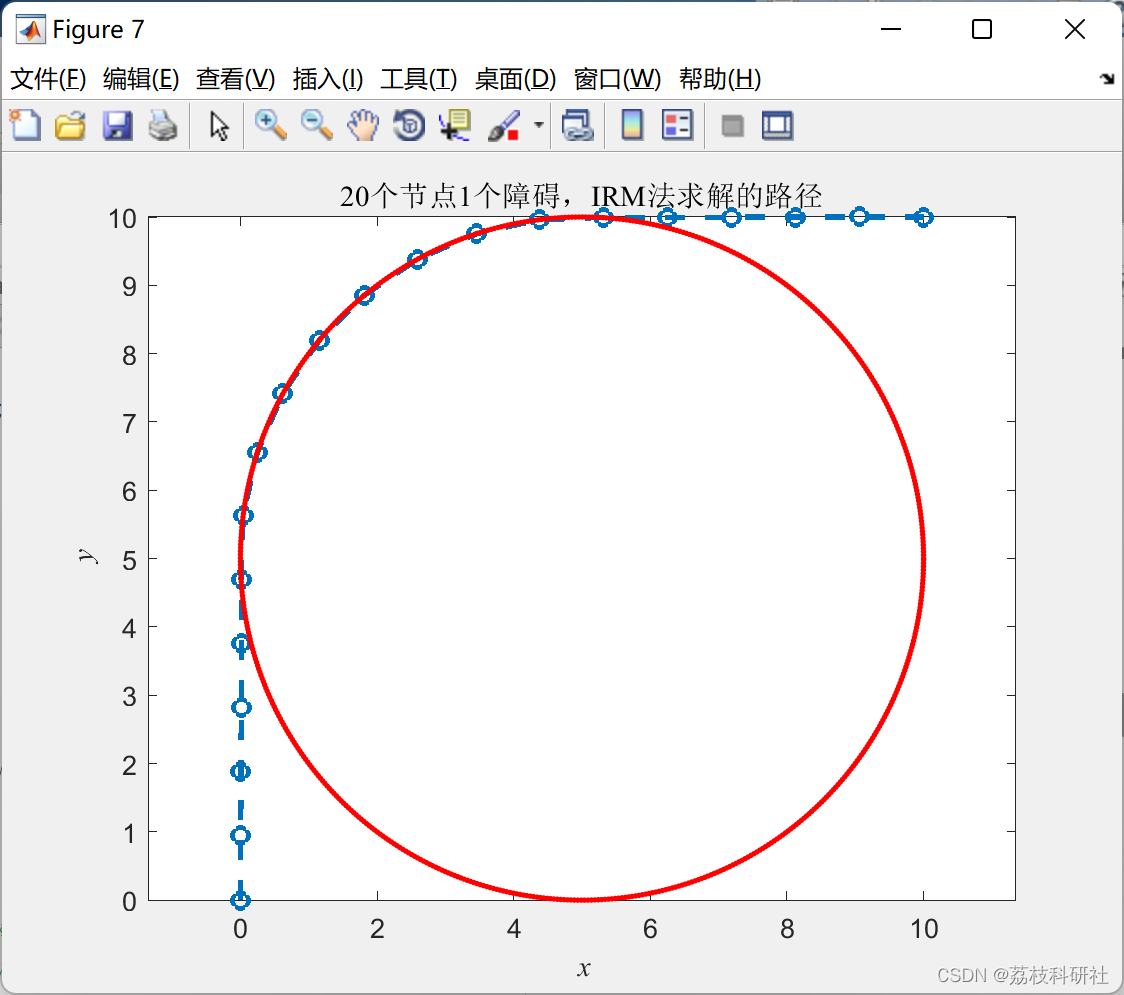
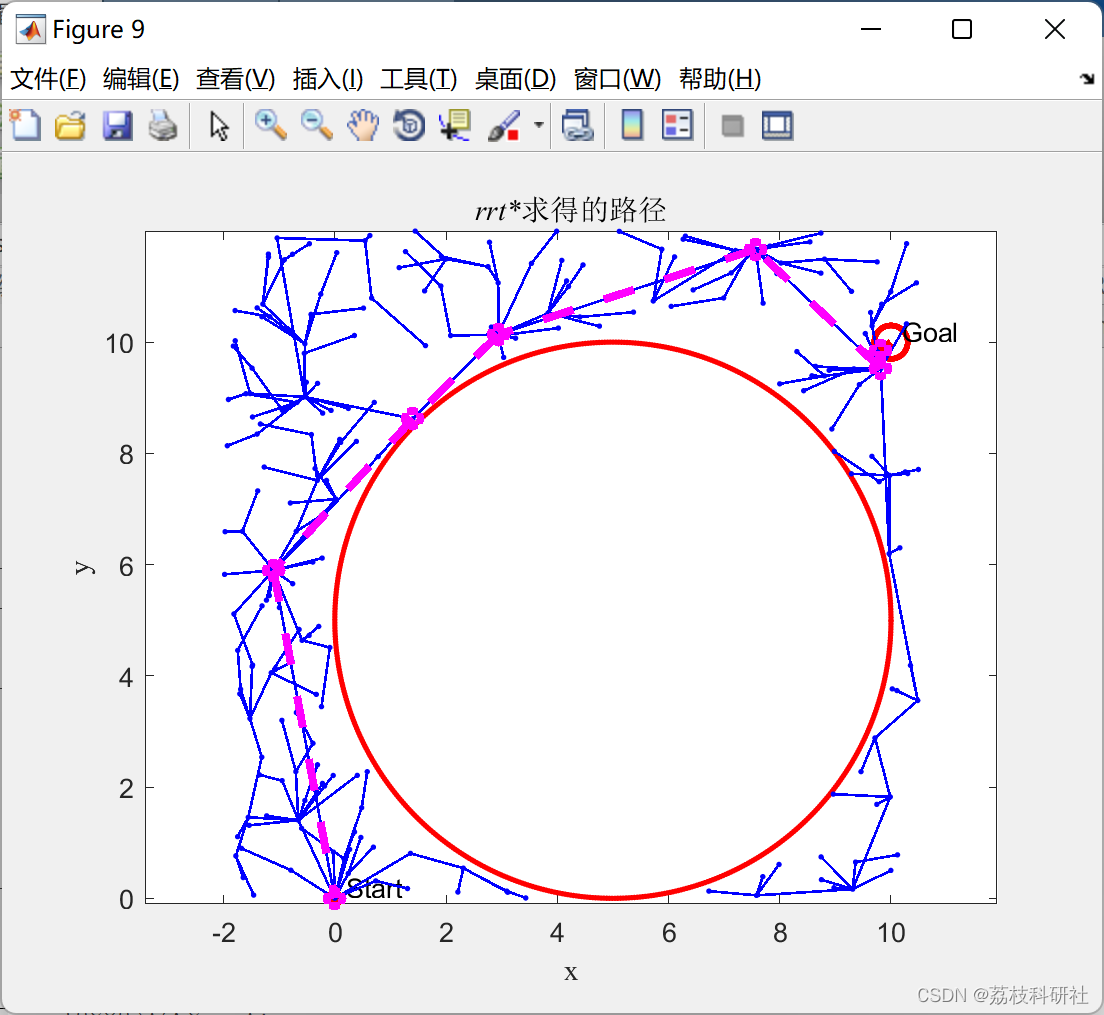

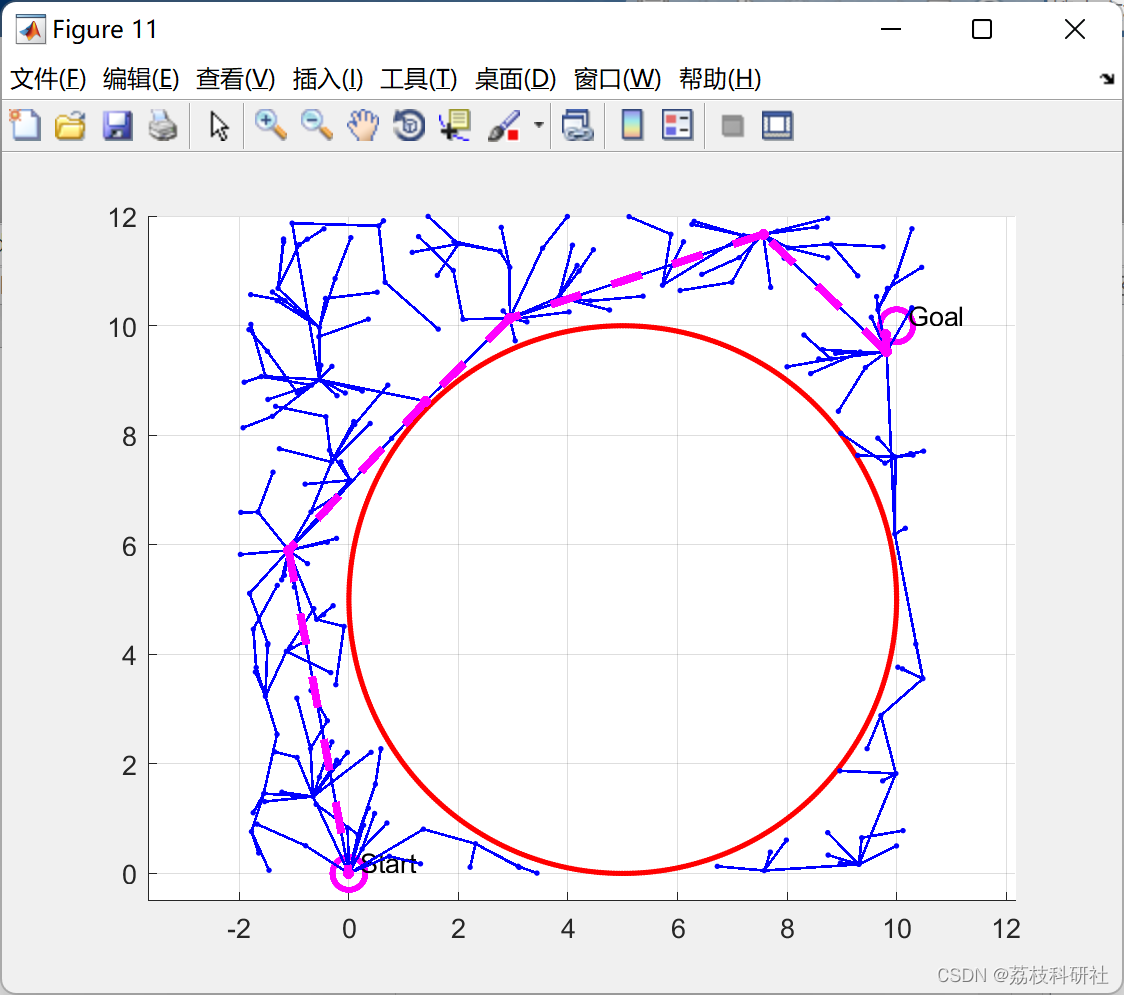
部分代码:
function result = RRTstar(param, p_start, p_goal)
% RRT*
% credit : Anytime Motion Planning using the RRT*, S. Karaman, et. al.
% calculates the path using RRT* algorithm
% param : parameters for the problem
% 1) threshold : stopping criteria (distance between goal and current
% node)
% 2) maxNodes : maximum nodes for rrt tree
% 3) neighborhood : distance limit used in finding neighbors
% 4) obstacle : must be rectangle-shaped #limitation
% 5) step_size : the maximum distance that a robot can move at a time
% (must be equal to neighborhood size) #limitation
% 6) random_seed : to control the random number generation
% p_start : [x;y] coordinates
% p_goal : [x;y] coordinates
% variable naming : when it comes to describe node, if the name is with
% 'node', it means the coordinates of that node or it is just an index of
% rrt tree
% rrt struct : 1) p : coordinate, 2) iPrev : parent index, 3) cost :
% distance
% obstacle can only be detected at the end points but not along the line
% between the points
% for cost, Euclidean distance is considered.
% output : cost, rrt, time_taken
% whether goal is reached or not, depends on the minimum distance between
% any node and goal
field1 = 'p'; %position
field2 = 'iPrev'; %partent
field3 = 'cost';
field4 = 'goalReached';
rng(param.random_seed);
tic;
start();
function start()
rrt(1) = struct(field1, p_start, field2, 0, field3, 0, field4, 0);
N = param.maxNodes; % iterations
j = 1;
% while endcondition>param.threshold %&& j<=N
while ~rrt(end).goalReached && j<=N
sample_node = getSample(param.searchFeild);
% plot(sample_node(1), sample_node(2), '.g');
% text(sample_node(1), sample_node(2), strcat('random',num2str(j)))
% idx = 1;
% mincost = rrt(1).cost + norm(sample_node-rrt(1).p);
% for k = 2:length(rrt)
% cost = rrt(k).cost + norm(sample_node-rrt(k).p);
% if cost < mincost
% % mincost = cost;
end
function rrt=setReachGoal(rrt)
rrt(end).goalReached = 1;
end
for i = 1: length(rrt)
p1 = rrt(i).p;
% rob.x = p1(1); rob.y=p1(2);
plot(p1(1),p1(2),'.b')
child_ind = find([rrt.iPrev]==i);
for j = 1: length(child_ind)
p2 = rrt(child_ind(j)).p;
plot([p1(1),p2(1)], [p1(2),p2(2)], 'b', 'LineWidth', 1);
end
end
end
end
result.time_taken = toc;
end
function [value,min_node_ind] = getFinalResult(rrt)
goal_ind = find([rrt.goalReached]==1);
if ~(isempty(goal_ind))
disp('Goal has been reached!');
rrt_goal = rrt(goal_ind);
value = min([rrt_goal.cost]);
min_node_ind = find([rrt.cost]==value);
if length(min_node_ind)>1
min_node_ind = min_node_ind(1);
end
else
disp('Goal has not been reached!');
for i =1:length(rrt)
norm_rrt(i) = norm(p_goal-rrt(i).p);
end
[~,min_node_ind]= min(norm_rrt);
value = rrt(min_node_ind).cost;
end
end
end
% if it is obstacle-free, return 1.
% otherwise, return 0
function free=isObstacleFree(node_free) %4
free = 1;
for i = 1: length(param.obstacles(:,1))
obs = param.obstacles(i,:);
% op1 = [obstacle(1), obstacle(2)];
% op2 = [op1(1)+obstacle(3), op1(2)];
% op3 = [op2(1), op1(2) + obstacle(4)];
% op4 = [op1(1), op3(2)];
nx = node_free(1);
ny = node_free(2);
ha = (nx-obs(1))^2 / obs(3)^2 + (ny-obs(2))^2 / obs(4)^2;
if (ha <= 1)
free = 0;
end
end
end
function new_node=steering(nearest_node, random_node) %3
dist = norm(random_node-nearest_node);
ratio_distance = param.step_size/dist;
if ratio_distance < 1
x = (1-ratio_distance).* nearest_node(1)+ratio_distance .* random_node(1);
y = (1-ratio_distance).* nearest_node(2)+ratio_distance .* random_node(2);
new_node = [x;y];
else
new_node = random_node;
end
end
function rrt = reWire(rrt, neighbors, parent, new) %8
for i=1:length(neighbors)
cost = rrt(new).cost + norm(rrt(neighbors(i)).p - rrt(new).p);
if (cost<rrt(neighbors(i)).cost)
% if norm(rrt(new).p-rrt(neighbors(i)).p)<param.step_size
% % plot(rrt(neighbors(i)).p(1), rrt(neighbors(i)).p(2), '.b');
% rrt(neighbors(i)).p = steering(rrt(new).p, rrt(neighbors(i)).p);
% end
% plot(rrt(neighbors(i)).p(1), rrt(neighbors(i)).p(2), '.m');
rrt(neighbors(i)).iPrev = new;
rrt(neighbors(i)).cost = cost;
end
end
end
function rrt = insertNode(rrt, parent, new_node) %7
rrt(end+1) = struct(field1, new_node, field2, parent, field3,...
rrt(parent).cost + norm(rrt(parent).p-new_node), field4, 0);
end
function parent = chooseParent(rrt, neighbors, nearest, new_node) %6
min_cost = getCostFromRoot(rrt, nearest, new_node);
parent = nearest;
for i=1:length(neighbors)
cost = getCostFromRoot(rrt, neighbors(i), new_node);
if (cost<min_cost)
min_cost = cost;
parent = neighbors(i);
end
end
end
function cost = getCostFromRoot(rrt, parent, child_node) %6.1
cost = rrt(parent).cost + norm(child_node - rrt(parent).p);
end
if isObstacleFree(node)
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1] Sun C , Liu Y C , Dai R , et al. Two Approaches for Path Planning of Unmanned Aerial Vehicles with Avoidance Zones[J]. Journal of Guidance Control & Dynamics, 2017, 40(8).
[2] Sun C , Dai R . An iterative approach to Rank Minimization Problems[C]// Decision & Control. IEEE, 2016.
🌈4 Matlab代码、文章详细讲解
相关文章:

【无人机路径规划】基于IRM和RRTstar进行无人机路径规划(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
Spring Boot中使用@Autowire装配接口是怎么回事?
在学习使用Spring Boot框架时候,发现了一个特别的现象UserMapper是一个接口,在另一个类中好像直接使用Autowired装配了一个UserMapper对象???我纳闷了一会儿,接口居然可以直接实例对象吗?根据我…...
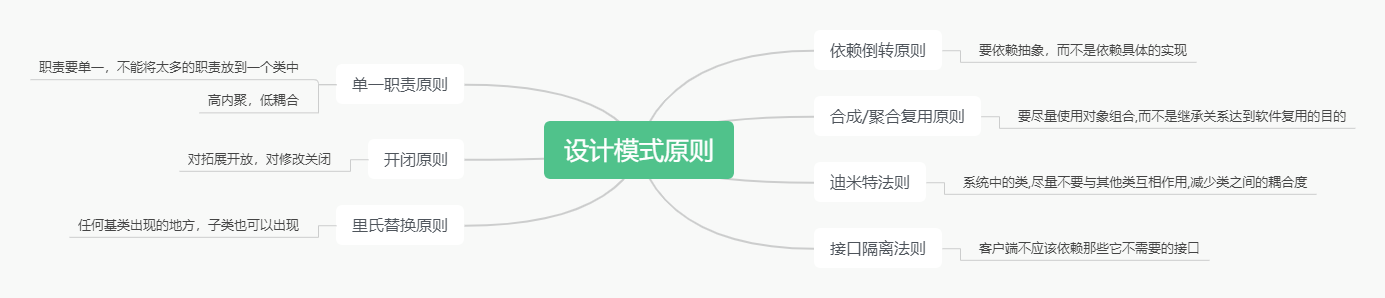
23种设计模式介绍(Python示例讲解)
文章目录一、概述二、设计模式七种原则三、设计模式示例讲解1)创建型模式1、工厂模式(Factory Method)【1】简单工厂模式(不属于GOF设计模式之一)【2】工厂方法模式2、抽象工厂模式(AbstractFactory&#x…...

初识Hadoop,走进大数据世界
文章目录数据!数据!遇到的问题Hadoop的出现相较于其他系统的优势关系型数据库网格计算本文章属于Hadoop系列文章,分享Hadoop相关知识。后续文章中会继续分享Hadoop的组件、MapReduce、HDFS、Hbase、Flume、Pig、Spark、Hadoop集群管理系统以及…...
加油站会员管理小程序实战开发教程14 会员充值
我们上篇介绍了会员开卡的业务,开卡是为了创建会员卡的信息。有了会员卡信息后我们就可以给会员进行充值。当然了充值这个业务是由会员自主发起的。 按照我们的产品原型,我们在我的页面以轮播图的形式循环展示当前会员的所有卡信息。这个会员卡信息需要先用变量从数据源读取…...

leetcode 1792. 最大平均通过率
一所学校里有一些班级,每个班级里有一些学生,现在每个班都会进行一场期末考试。给你一个二维数组 classes ,其中 classes[i] [passi, totali] ,表示你提前知道了第 i 个班级总共有 totali 个学生,其中只有 passi 个学…...

15-基础加强-2-xml(约束)枚举注解
文章目录1.xml1.1概述【理解】(不用看)1.2标签的规则【应用】1.3语法规则【应用】1.4xml解析【应用】1.5DTD约束【理解】1.5.1 引入DTD约束的三种方法1.5.2 DTD语法(会阅读,然后根据约束来写)1.6 schema约束【理解】1.6.1 编写schema约束1.6.…...
)
13:高级篇 - CTK 事件管理机制(signal/slot)
作者: 一去、二三里 个人微信号: iwaleon 微信公众号: 高效程序员 在《12:高级篇 - CTK 事件管理机制(sendEvent/postEvent)》一文中,我们介绍了如何进行插件间通信 - sendEvent()/postEvent() + ctkEventHandler。然而,除了这种方式之外,EventAdmin 还提供了另一种方…...
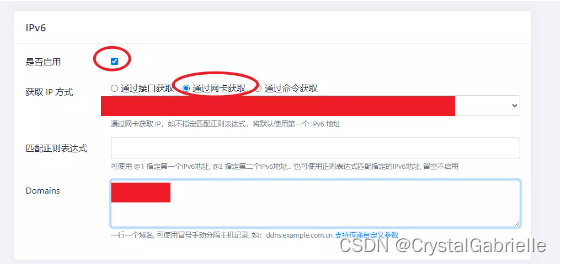
群晖-第1章-IPV6的DDNS
群晖-第1章-IPV6的DDNS 方案:腾讯云群晖DS920 本文参考群晖ipv6 DDNS-go教程-牧野狂歌,感谢原作者的分享。 这篇文章只记录了我需要的部分,其他的可以查看原文,原文还记录了更多的内容,可能帮到你。 一、购买域名 …...
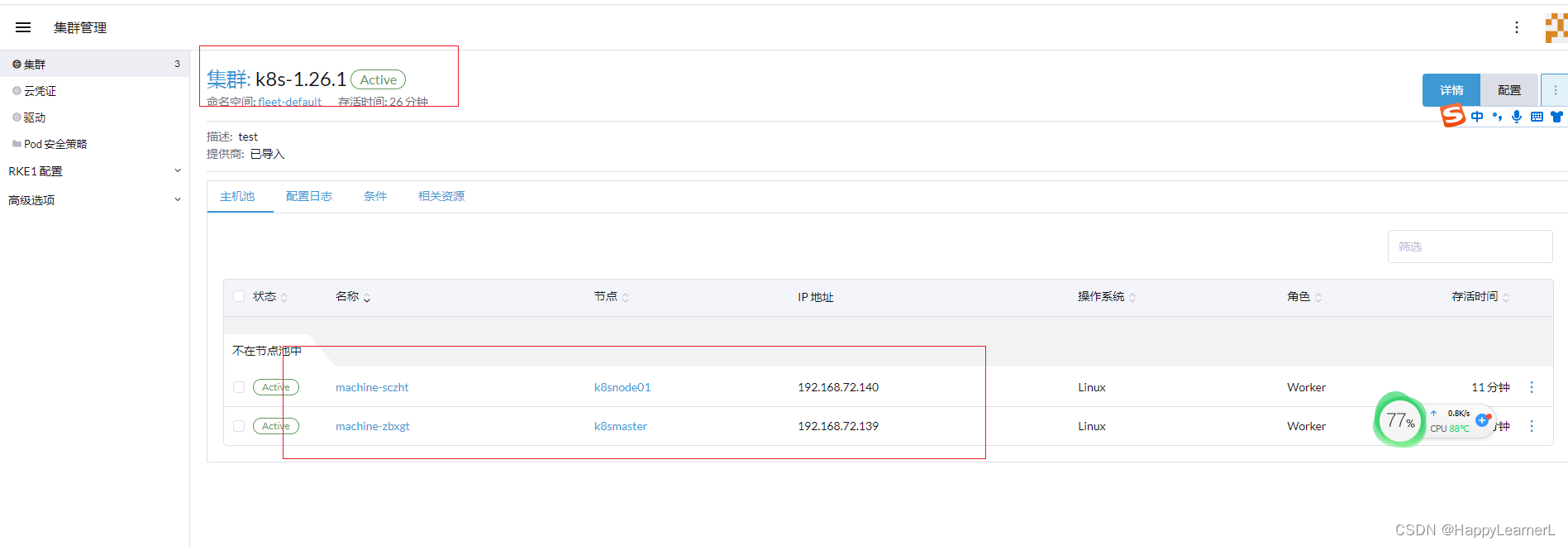
centos7系统-kubeadm安装k8s集群(v1.26版本)亲测有效,解决各种坑可供参考
文章目录硬件要求可省略的步骤配置虚拟机ip设置阿里镜像源各服务器初始化配置配置主节点的主机名称配置从节点的主机名称配置各节点的Host文件关闭各节点的防火墙关闭selinux永久禁用各节点的交换分区同步各节点的时间将桥接的IPv4流量传递到iptables的链(三台都执行…...
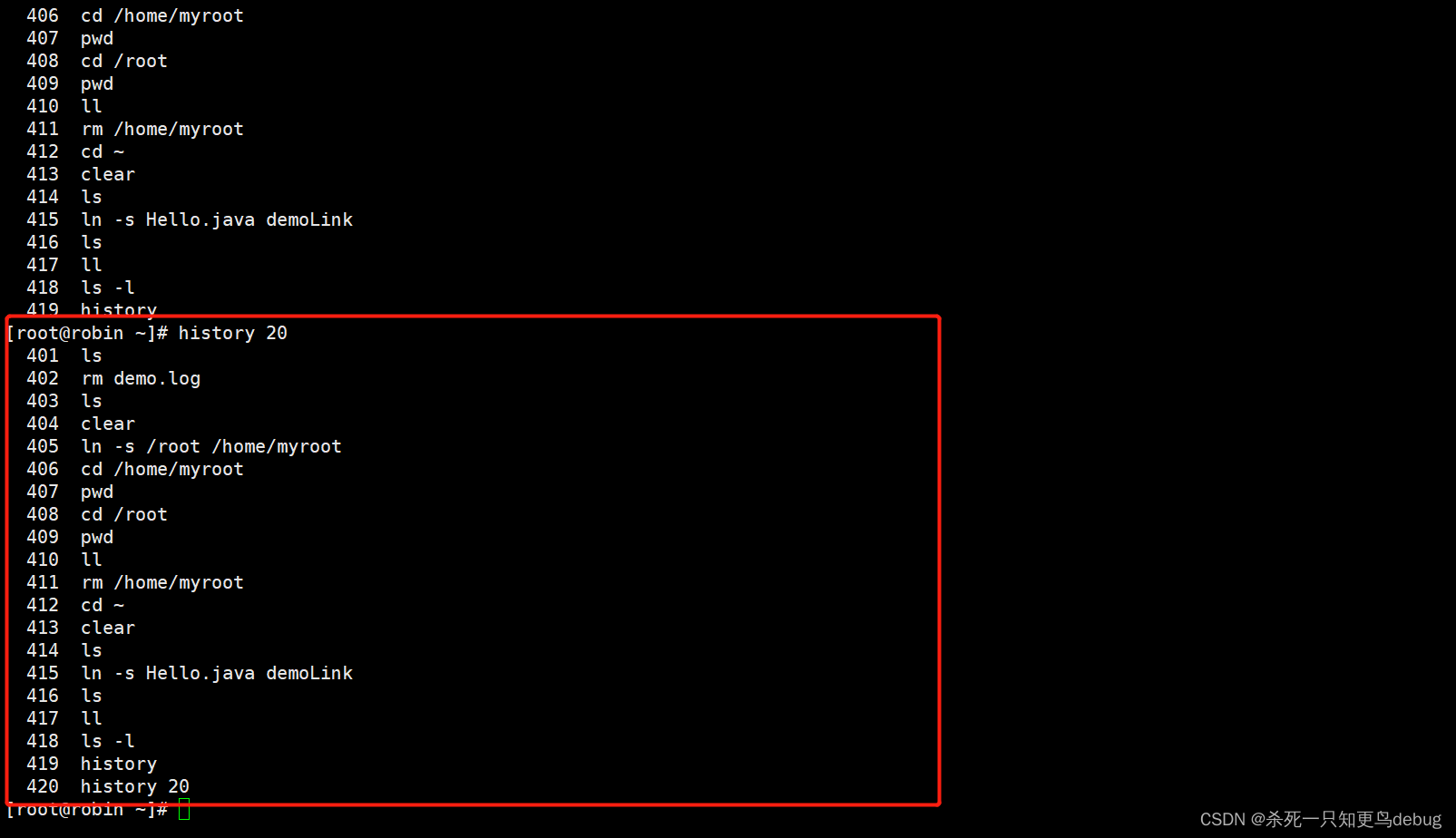
帮助指令 man ,help及文档常用管理指令
帮助指令 man,help 1. man 当我们想要了解某个命令如何使用,及选项的含义是什么以及配置文件的帮助信息时,可以使用 man [命令或配置文件],这样便可以获得到帮助提示信息了。 语法格式:man [命令或者配置文件] 比如…...
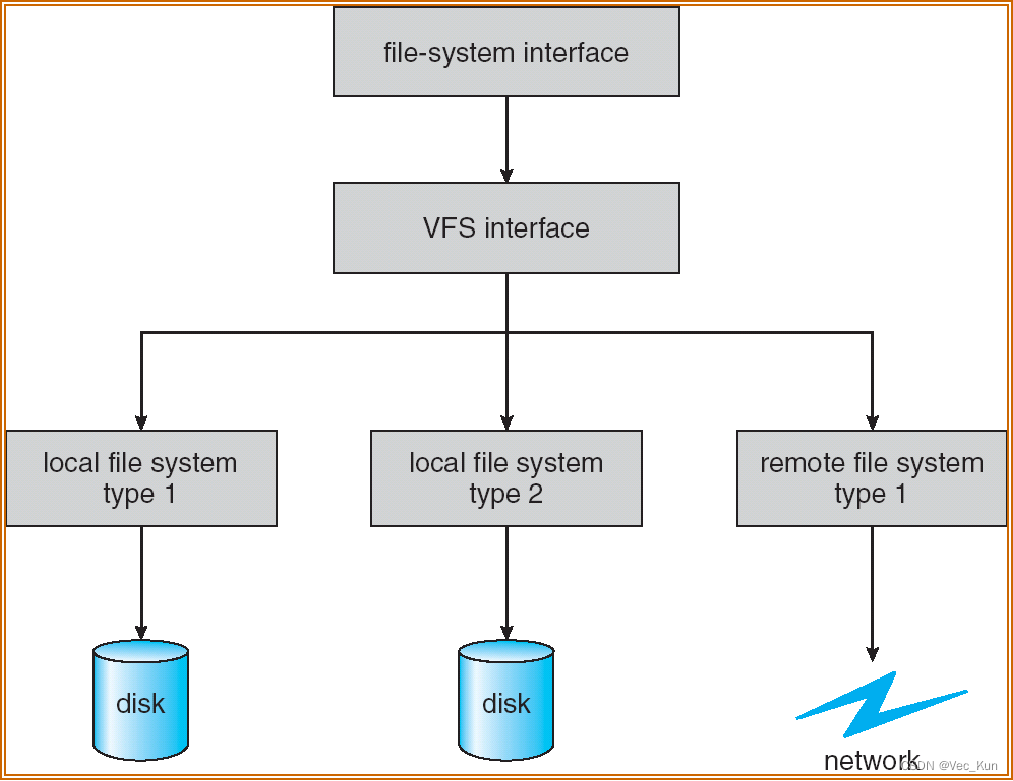
电子科技大学操作系统期末复习笔记(五):文件管理
目录 前言 文件管理:基础 基本概念 文件 文件系统 文件系统的实现模型 文件的组成 文件名 文件分类 文件结构 逻辑结构 物理结构 练习题 文件管理:目录 文件控制块FCB FCB:File Control Block FCB信息 目录 基本概念 目…...
SpringBoot+ActiveMQ-发布订阅模式(生产端)
SpringBootActiveMQ-发布订阅模式(生产端)Topic 主题* 消息消费者(订阅方式)消费该消息* 消费生产者将发布到topic中,同时有多个消息消费者(订阅)消费该消息* 这种方式和点对点方式不同…...
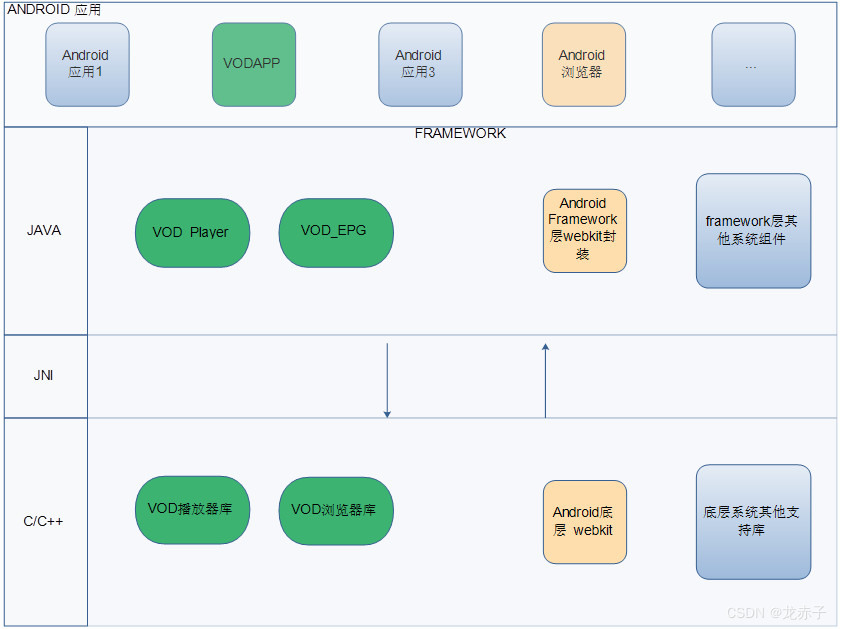
Android实例仿真之三
目录 四 Android架构探究 五 大骨架仿真 六 Android实例分析思路拓展 四 Android架构探究 首先,Android系统所带来的好处,就在于它本身代码的开放性,这提供了一个学习、借鉴的平台。这对分析仿真而言,本身就是一大利好…...
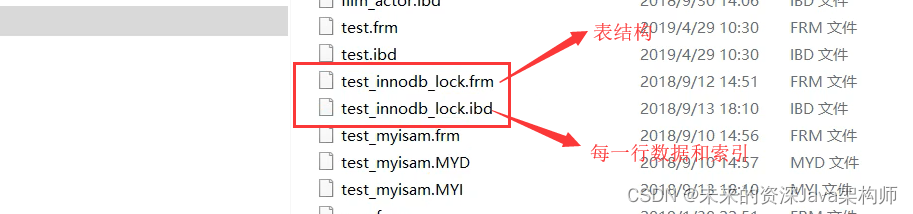
关于MySQL的limit优化
1、前提 提示:只适用于InnoDB引擎 2、InnoDB存储特点 它把索引和数据放在了一个文件中,就是聚集索引。这与MyISAM引擎是不一样的。 3、SQL示例 -- 给cve字段建立索引 select * from cnnvd where cveCVE-2022-24808 limit 300000,10;由于M…...

Java-Stream流基本使用
collection.stream将会破坏原有的数据结构,可以通过collect方法收集,可以用Collectors提供的构造器,add等方法构造形成新的数据结构。 HashSet<List<Integer>> rs new HashSet<>(); rs.stream().toList();Collection集合转…...

Liunx(狂神课堂笔记)
一.常用命令 1. cd 切换目录 cd ./* 当前目录cd /* 绝对路径cd .. 返回上一级目录cd ~ 回到当前目录pwd …...

【史上最全面esp32教程】点灯大师篇
文章目录前言ESP32简介认识arduino的两个函数点灯步骤函数介绍LED灯闪烁流水灯总结前言 esp32有很多的功能,例如wifi,蓝牙等,这节我们学习最简单的点灯。 提示:以下是本篇文章正文内容,下面案例可供参考 ESP32简介 …...
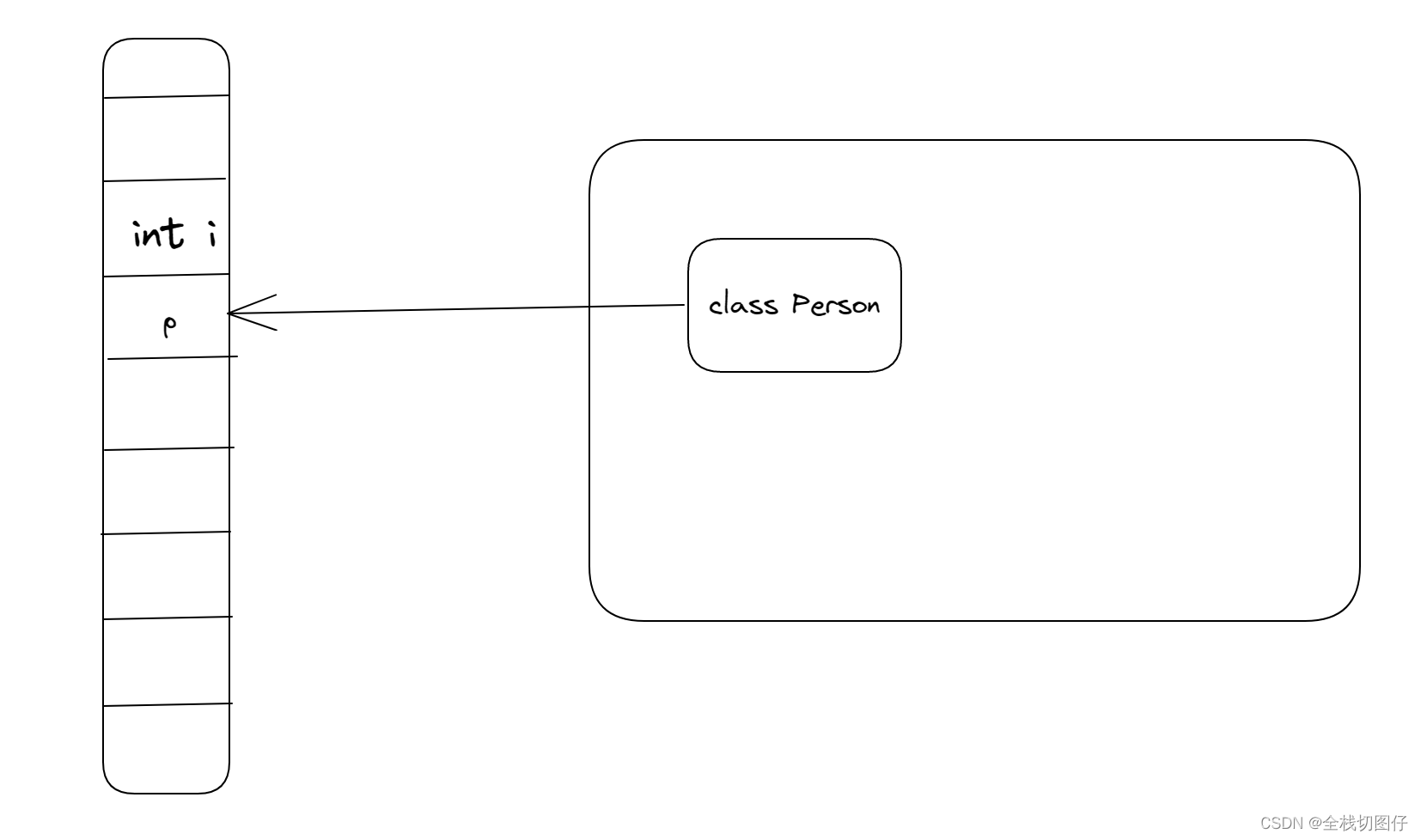
【Java 面试合集】内存中为什么要区分栈和堆
内存中为什么要区分栈和堆 1. 概述 嗨,大家好Java 面试合集又来了,今天我们分享的主题很大众化以及普通。无论是Java 语言本身还是别的语言都会有所涉及,但是今天我们从Java角度来讲下 2. 分析 今天我们会从多个方向来分享这个话题 2.1 栈是…...
【NLP实战】Python字符串处理
一、Python字符串基本操作 1. 去掉前后的特殊字符(strip) Python的strip操作可以去除字符串前后的空格(不改变原串)下例将前后的空格均删掉👇 str 人工智能 str.strip() # OUT:人工智能rstrip删除右边的空格&a…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

《Docker》架构
文章目录 架构模式单机架构应用数据分离架构应用服务器集群架构读写分离/主从分离架构冷热分离架构垂直分库架构微服务架构容器编排架构什么是容器,docker,镜像,k8s 架构模式 单机架构 单机架构其实就是应用服务器和单机服务器都部署在同一…...

