【数据结构】二叉树链式结构的实现及其常见操作
目录
1.手搓二叉树
2.二叉树的遍历
2.1前序、中序以及后序遍历
2.2二叉树的层序遍历
3.二叉树的常见操作
3.1求二叉树节点数量
3.2求二叉树叶子节点数量
3.3求二叉树第k层节点个数
3.3求二叉树的深度
3.4二叉树查找值为x的节点
4.二叉树的销毁
1.手搓二叉树
在学习二叉树的基本操作前,需先要创建一棵二叉树,然后才能学习其相关的基本操作。由于现在我们对二叉树结构掌握还不够深入,为了降低学习成本,此处手动快速创建一棵简单的二叉树,快速进入二叉树操作学习,等二叉树结构了解的差不多时,我们反过头再来研究二叉树真正的创建方式。

定义二叉树的节点:
typedef int BTDataType;
typedef struct BinaryTreeNode
{struct BinaryTreeNode* left;struct BinaryTreeNode* right;BTDataType data;
}BTNode;根据上图的二叉树结构手写二叉树:
BTNode* BuyNode(BTDataType data)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));assert(node);node->data = data;node->left = node->right = NULL;return node;
}BTNode* CreatBinaryTree()
{BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;return node1;
}这样我们就写出了一个简单的二叉树。
2.二叉树的遍历
2.1前序、中序以及后序遍历
学习二叉树结构,最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则,依次对二叉树中的节点进行相应的操作,并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。 遍历是二叉树上最重要的运算之一,也是二叉树上进行其它运算的基础。
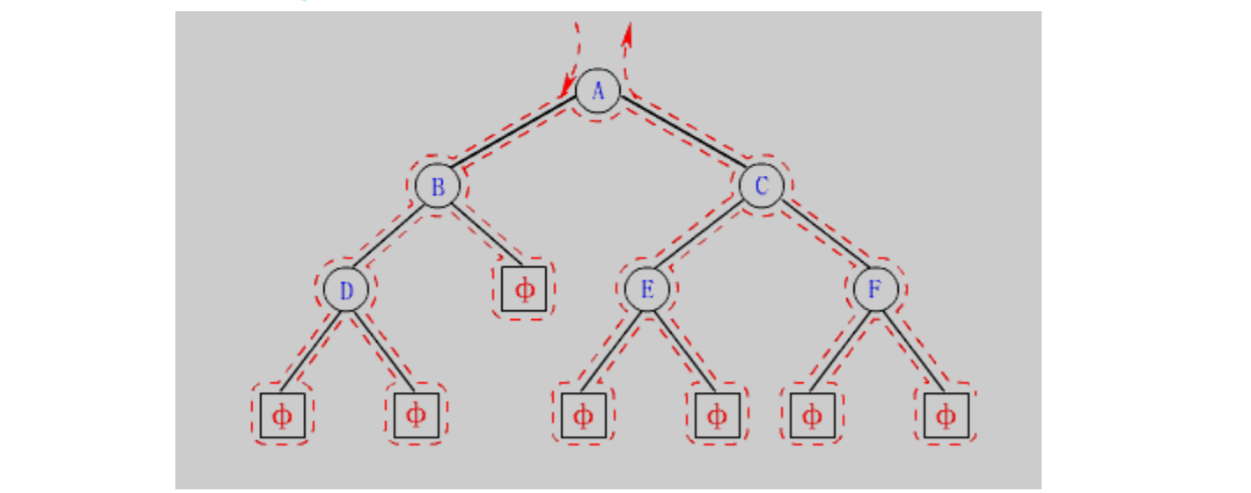
按照规则,二叉树的遍历有:前序/中序/后序的递归结构遍历:
- 前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。
- 中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中(间)。
- 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。
由于被访问的结点必是某子树的根,所以N(Node)、L(Left subtree)和R(Right subtree)又可解释为 根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。

对于二叉树的遍历,代码写起来很简单,但是对于初学者来说,要理解起来就有点难了,这里先给出三种遍历的代码,大家可以先看看:
前序遍历
void PreOrder(BTNode* root)
{if (root == NULL){printf("# ");return;}printf("%d ", root->data);PreOrder(root->left);PreOrder(root->right);
}中序遍历
void InOrder(BTNode* root)
{if (root == NULL){printf("# ");return;}InOrder(root->left);printf("%d ", root->data);InOrder(root->right);
}后序遍历
void PostOrder(BTNode* root)
{if (root == NULL){printf("# ");return;}PostOrder(root->left);PostOrder(root->right);printf("%d ", root->data);
}看完代码后,是不是觉得这三种遍历都非常的相似呢?我们在编译器上运行一下三种遍历的代码:
int main()
{BTNode* root = CreatBinaryTree();PreOrder(root);printf("\n");InOrder(root);printf("\n");PostOrder(root);return 0;
}运行结果:

前序遍历的递归展开图:

中序遍历和后续遍历和这图也差不多。
2.2二叉树的层序遍历
二叉树的层序遍历是一种广度优先搜索(BFS)的方法。它按层级顺序逐层遍历二叉树,即从根节点开始,先遍历第一层节点,然后遍历第二层节点,依次类推,直到遍历完所有层级。
实现层序遍历的一种常见方法是使用队列。具体思路如下:
- 创建一个空队列,并将根节点入队。
- 循环执行以下步骤,直到队列为空:
- 出队一个节点,将其值存储到结果列表中。
- 若该节点有左孩子,则将左孩子入队。
- 若该节点有右孩子,则将右孩子入队。
这样,当队列为空时,遍历过程就完成了,结果列表中存储着层序遍历的结果。

下面代码的使用了C++STL中的队列来完成,避免了手写队列的麻烦:
void LevelOrder(BTNode* root)
{assert(root);queue<BTNode*> a;a.push(root);while (!a.empty()){BTNode* front = a.front();a.pop();printf("%d ", front->data);if (front->left){a.push(front->left);}if (front->right){a.push(front->right);}}
}int main()
{BTNode* root = CreatBinaryTree();LevelOrder(root);return 0;
}输出结果:

3.二叉树的常见操作
3.1求二叉树节点数量
方法一:
定义一个全局变量count,然后遍历每一个节点,每遍历一个节点,count就自加1
代码:
int count = 0;
void TreeSize1(BTNode* root)
{if (root == NULL){return;}count++;TreeSize1(root->left);TreeSize1(root->right);
}
int main()
{BTNode* root = CreatBinaryTree();count = 0;TreeSize1(root);printf("%d\n", count);return 0;
}方法二:
int TreeSize2(BTNode* root)
{if (root == NULL){return 0;}return TreeSize2(root->left) + TreeSize2(root->right) + 1;
}
int main()
{BTNode* root = CreatBinaryTree();printf("TreeSize2: %d\n", TreeSize2(root));return 0;
}首先检查根节点是否为空,如果为空,说明这是一个空树,直接返回0。如果根节点不为空,则递归调用自身来计算左子树和右子树的节点数,然后将左子树节点数、右子树节点数以及根节点本身(1个节点)的数量相加,最后返回结果。
通过这种递归的方式,函数可以计算出二叉树中所有节点的总数。
3.2求二叉树叶子节点数量
具体思路:
首先检查根节点是否为空,如果为空,说明这是一个空树,直接返回 0。接着,通过判断根节点的左子树和右子树是否都为空来确定当前节点是否为叶子节点。如果是叶子节点,返回 1。如果不是叶子节点,递归调用自身来计算左子树和右子树的叶子节点数,并将其相加作为结果返回。
int TreeLeafSize(BTNode* root)
{if (root == NULL) return 0;if (root->left == NULL && root->right == NULL) return 1;return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}
int main()
{BTNode* root = CreatBinaryTree();printf("TreeLeafSize: %d\n", TreeLeafSize(root));return 0;
}3.3求二叉树第k层节点个数
思路:
首先检查根节点是否为空,如果为空,说明这是一个空树,直接返回0。如果k等于1,说明当前层即为目标层,返回1。如果k大于1,则递归调用自身来计算左子树和右子树中第k-1层节点的数量,并将其相加作为结果返回。
通过这种递归的方式,函数可以计算出二叉树中第k层节点的总数。
int TreeKLevel(BTNode* root, int k)
{assert(k >= 1);if (root == NULL) return 0;if (k == 1) return 1;return TreeKLevel(root->left, k - 1) + TreeKLevel(root->right, k - 1);
}
int main()
{BTNode* root = CreatBinaryTree();printf("TreeKLevel: %d\n", TreeKLevel(root, 2));//第2层节点数量printf("TreeKLevel: %d\n", TreeKLevel(root, 3));//第3层节点数量printf("TreeKLevel: %d\n", TreeKLevel(root, 4));//第4层节点数量return 0;
}函数的递归展开图:

3.3求二叉树的深度
int TreeDepth(BTNode* root)
{if (root == NULL) return 0;int l = TreeDepth(root->left); //左子树的深度int r = TreeDepth(root->right); //右子树的深度return (l > r ? l : r) + 1; //返回左右子树深度的较大值加自身的深度1
}
int main()
{BTNode* root = CreatBinaryTree();printf("TreeDepth: %d\n", TreeDepth(root));return 0;
}首先检查根节点是否为空,如果为空,说明这是一个空树,直接返回深度0。接着,函数通过递归调用自身来计算左子树和右子树的深度,分别将结果存储在变量l和r中。然后,通过比较l和r的大小,选择较大的值,并将其加1(代表当前节点的深度),作为整棵二叉树的深度。
通过这种递归的方式,函数可以计算出二叉树的深度(高度)。
3.4二叉树查找值为x的节点
在二叉树查找值为x的节点时,尽量使用前序遍历,可以提高效率。
BTNode* TreeFind(BTNode* root, BTDataType x)
{if (root == NULL) return NULL;if (root->data == x) return root;BTNode* ret1 = TreeFind(root->left, x);if (ret1){return ret1;}BTNode* ret2 = TreeFind(root->right, x);if (ret2){return ret2;}return NULL;
}int main()
{BTNode* root = CreatBinaryTree();BTNode* ret = TreeFind(root, 3);if (ret){printf("找到了:%d\n", ret->data);}else{printf("找不到\n");}return 0;
}首先检查根节点是否为空,如果为空,说明这是一个空树,直接返回NULL。接着,函数检查当前节点的数据是否等于目标值x,如果等于,说明找到了目标节点,返回指向当前节点的指针。如果不等于,递归调用函数分别在左子树和右子树中查找目标值x,如果返回的指针非空,说明在子树中找到了目标节点,直接返回该指针。如果左右子树都没有找到目标节点,则返回NULL。
通过这种递归的方式,函数可以在二叉树中查找特定值的节点,并返回指向该节点的指针。如果找不到目标值,则返回NULL。
4.二叉树的销毁
对于二叉树的销毁,我们不能使用先序遍历,因为如果使用先序遍历,会将二叉树的根节点先销毁掉,这样就无法找到根节点的左子树和右子树了,如果一定要使用先序遍历,那就得先把节点的左子树和右子树先保存下来。但如果使用后序遍历,就可以轻松解决了。
采用后序遍历销毁,按照左孩子,右孩子,根节点的顺序销毁一颗二叉树。
void TreeDestory(BTNode* root)
{if (root == NULL){return;}TreeDestory(root->left);TreeDestory(root->right);free(root);
}
int main()
{BTNode* root = CreatBinaryTree();PreOrder(root);TreeDestory(root);root = NULL;
}
相关文章:

【数据结构】二叉树链式结构的实现及其常见操作
目录 1.手搓二叉树 2.二叉树的遍历 2.1前序、中序以及后序遍历 2.2二叉树的层序遍历 3.二叉树的常见操作 3.1求二叉树节点数量 3.2求二叉树叶子节点数量 3.3求二叉树第k层节点个数 3.3求二叉树的深度 3.4二叉树查找值为x的节点 4.二叉树的销毁 1.手搓二叉树 在学习…...
从零实战SLAM-第九课(后端优化)
在七月算法报的班,老师讲的蛮好。好记性不如烂笔头,关键内容还是记录一下吧,课程入口,感兴趣的同学可以学习一下。 --------------------------------------------------------------------------------------------------------…...

Python Opencv实践 - 图像金字塔
import cv2 as cv import numpy as np import matplotlib.pyplot as pltimg cv.imread("../SampleImages/pomeranian.png", cv.IMREAD_COLOR) print(img.shape)#图像上采样 #cv.pyrUp(src, dstNone, dstsizeNone, borderTypeNone) #参考资料:https://blo…...
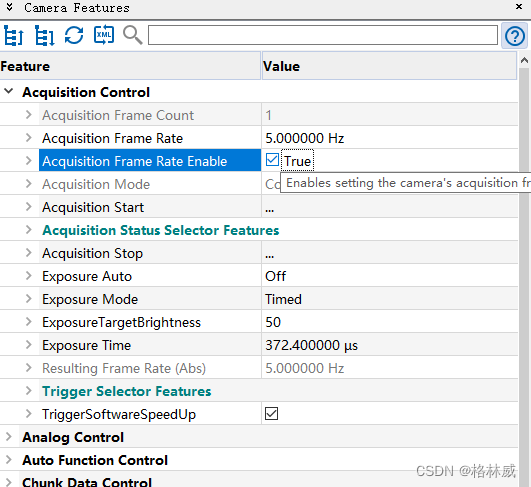
Baumer工业相机堡盟工业相机如何通过BGAPI SDK设置相机的固定帧率(C++)
Baumer工业相机堡盟工业相机如何通过BGAPI SDK设置相机的固定帧率(C) Baumer工业相机Baumer工业相机的固定帧率功能的技术背景CameraExplorer如何查看相机固定帧率功能在BGAPI SDK里通过函数设置相机固定帧率 Baumer工业相机通过BGAPI SDK设置相机固定帧…...
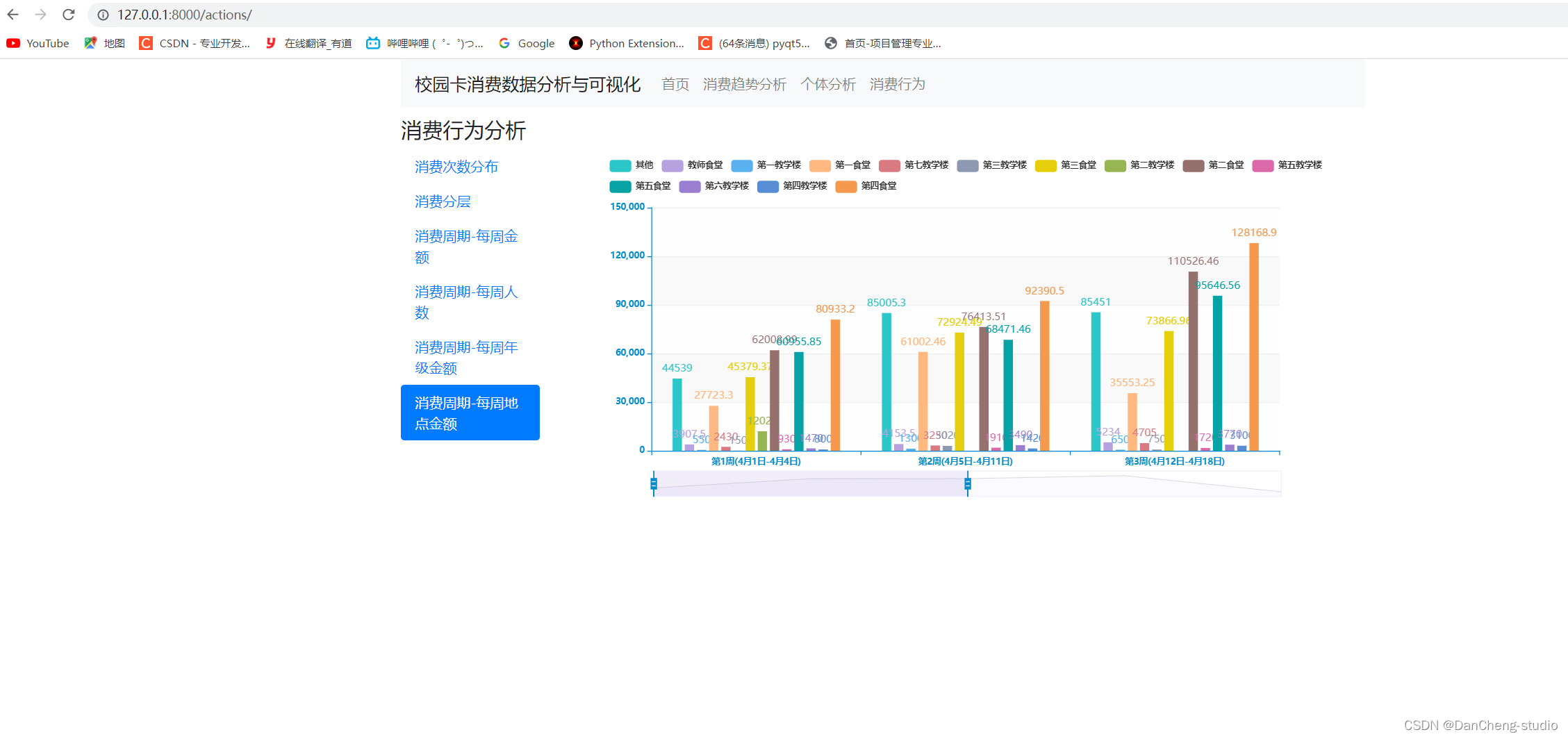
计算机竞赛 python+大数据校园卡数据分析
0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 基于yolov5的深度学习车牌识别系统实现 🥇学长这里给一个题目综合评分(每项满分5分) 难度系数:4分工作量:4分创新点:3分 该项目较为新颖&am…...

DNNGP模型解读-early stopping 和 batch normalization的使用
一、考虑的因素(仅代表个人观点) 1.首先我们看到他的这篇文章所考虑的不同方面从而做出的不同改进,首先考虑到了对于基因组预测的深度学习方法的设计 ,我们设计出来这个方法就是为了基因组预测而使用,这也是主要目的&…...
【目标检测】目标检测 相关学习笔记
目标检测算法 PASCALVOC2012数据集 挑战赛主要分为 图像分类 目标检测 目标分割 动作识别 数据集分为四个大类 交通(飞机 船 公交车 摩托车) 住房(杯子 椅子 餐桌 沙发) 动物(鸟 猫 奶牛 狗 马 羊) 其他&a…...
)
面试攻略,Java 基础面试 100 问(十六)
反射使用步骤(获取Class对象、调用对象方法) 获取想要操作的类的Class对象,他是反射的核心,通过Class对象我们可以任意调用类的方法。 调用 Class 类中的方法,既就是反射的使用阶段。 使用反射 API 来操作这些信息。 什么是 java 序列化&…...

章节5:脚本注入网页-XSS
章节5:脚本注入网页-XSS XSS :Cross Site Script 恶意攻击者利用web页面的漏洞,插入一些恶意代码,当用户访问页面的时候,代码就会执行,这个时候就达到了攻击的目的。 JavaScript、Java、VBScript、Activ…...
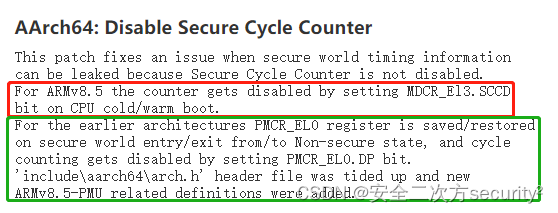
ATF(TF-A)安全通告 TFV-5 (CVE-2017-15031)
安全之安全(security)博客目录导读 ATF(TF-A)安全通告汇总 目录 一、ATF(TF-A)安全通告 TFV-5 (CVE-2017-15031) 二、CVE-2017-15031 一、ATF(TF-A)安全通告 TFV-5 (CVE-2017-15031) Title 未初始化或保存/恢复PMCR_EL0可能会泄露安全世界的时间信息 CVE ID CVE-2017-1503…...
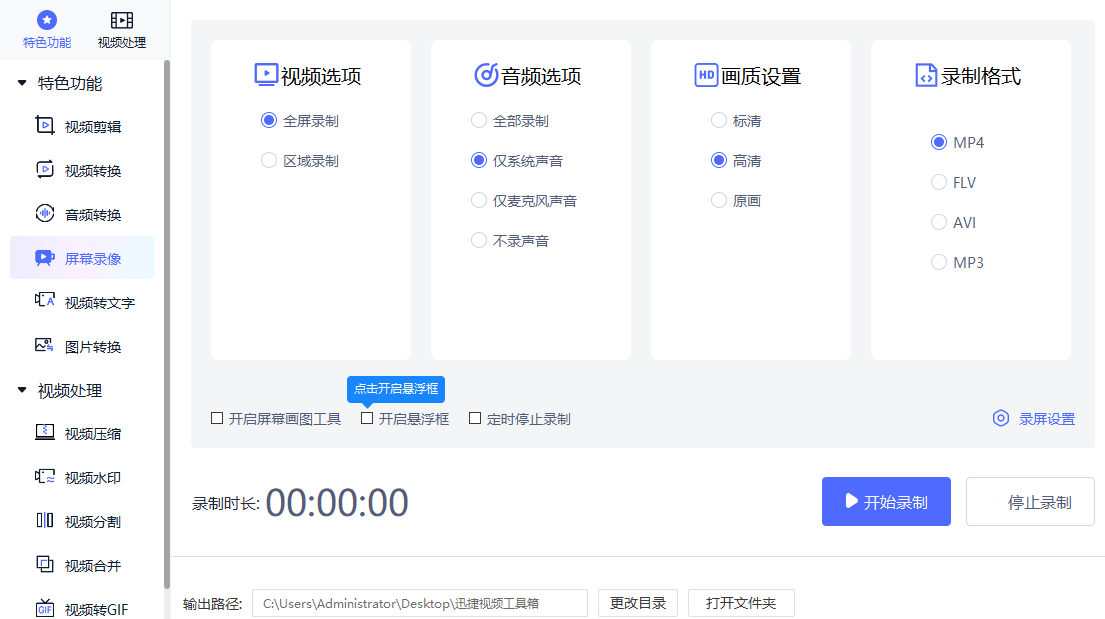
迅捷视频工具箱:多功能音视频处理软件
这是一款以视频剪辑、视频转换、屏幕录像等特色功能为主,同时附带有视频压缩、视频分割、视频合并等常用视频处理功能为主的视频编辑软件。该软件操作简单易用,即使没有视频处理经验的用户也可以轻松上手。将视频添加到工具箱对应功能后,简单…...

linux--fork()详解
fork() 参考链接:链接 进程控制原语包括:进程的建立、进程的撤销、进程的等待和进程的唤醒。 fork,在英语用译为叉子,形状像Y,反过来就如下图: 就是本来只有一个进行app,然后它调用了fork()函数…...

go_并发编程(1)
go并发编程 一、 并发介绍1,进程和线程2,并发和并行3,协程和线程4,goroutine 二、 Goroutine1,使用goroutine1)启动单个goroutine2)启动多个goroutine 2,goroutine与线程3࿰…...

第一百一十五回 权限管理包permission_handler
文章目录 概念介绍使用方法示例代码经验分享 我们在上一章回中介绍了局部动态列表相关的内容,本章回中将介绍权限管理包 permission_hanadler.闲话休提,让我们一起Talk Flutter吧。 概念介绍 权限是使用某种功能的授权,比如使用手机上的相机…...
【机器学习】sklearn数据集的使用,数据集的获取和划分
「作者主页」:士别三日wyx 「作者简介」:CSDN top100、阿里云博客专家、华为云享专家、网络安全领域优质创作者 「推荐专栏」:对网络安全感兴趣的小伙伴可以关注专栏《网络安全入门到精通》 sklearn数据集 二、安装sklearn二、获取数据集三、…...

Mysql之 optimizer_trace 相关总结
Mysql之 optimizer_trace 相关总结 MySQL官网介绍:https://dev.mysql.com/doc/dev/mysql-server/latest/PAGE_OPT_TRACE.html 1. 简介 MySQL优化器可以生成Explain执行计划,通过执行计划查看sql是否使用了索引,使用了哪种索; 但…...

【Linux命令详解 | wget命令】 wget命令用于从网络下载文件,支持HTTP、HTTPS和FTP协议
文章标题 简介一,参数列表二,使用介绍1. 基本文件下载2. 递归下载整个网站3. 限制下载速率4. 防止SSL证书校验5. 断点续传6. 指定保存目录7. 自定义保存文件名8. 增量下载9. 使用HTTP代理10. 后台下载 总结 简介 在编程世界中,处理网络资源是…...

DockePod信号处理机制与僵尸进程优化
Docke&Pod信号处理与僵尸进程优化 容器与信号的关系 SIGTERM信号:程序结束(terminate)信号,这是用来终止进程的标准信号,也是 kill 、 killall 、 pkill 命令所发送的默认信号。与SIGKILL不同的是该信号可以被阻塞和处理。通常用来要求程…...

NetApp StorageGRID 对象存储,使您能够跨公有、私有云和混合多云环境管理非结构化数据
NetApp StorageGRID 对象存储,使您能够跨公有、私有云和混合多云环境管理非结构化数据 主要优势 智能:了解行业领先的数据生命周期管理软件。 • 借助 NetApp StorageGRID 基于对象的存储解决方案的数据管理功能、您可以从大型非结构化数据中获得高价值…...

使用Java服务器实现UDP消息的发送和接收(多线程)
目录 简介:1. 导入必要的库2. 创建服务器端代码3. 创建客户端代码4. 实现多线程处理5. 测试运行示例代码:函数说明服务器端代码说明:客户端代码说明: 总结: 简介: 在本篇博客中,我们将介绍如何…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

LangFlow技术架构分析
🔧 LangFlow 的可视化技术栈 前端节点编辑器 底层框架:基于 (一个现代化的 React 节点绘图库) 功能: 拖拽式构建 LangGraph 状态机 实时连线定义节点依赖关系 可视化调试循环和分支逻辑 与 LangGraph 的深…...

Python网页自动化Selenium中文文档
1. 安装 1.1. 安装 Selenium Python bindings 提供了一个简单的API,让你使用Selenium WebDriver来编写功能/校验测试。 通过Selenium Python的API,你可以非常直观的使用Selenium WebDriver的所有功能。 Selenium Python bindings 使用非常简洁方便的A…...

Kubernetes 节点自动伸缩(Cluster Autoscaler)原理与实践
在 Kubernetes 集群中,如何在保障应用高可用的同时有效地管理资源,一直是运维人员和开发者关注的重点。随着微服务架构的普及,集群内各个服务的负载波动日趋明显,传统的手动扩缩容方式已无法满足实时性和弹性需求。 Cluster Auto…...

