2.19 索引和事务
一.联合查询
面试问题:
聚合查询与联合查询的区别
聚合查询是行与行之间的数据加工
聚合函数 :count,sum,avg...
group by 进行分组,指定列的值,相同的记录合并到同一个组,每个组又可以分别进行聚合查询
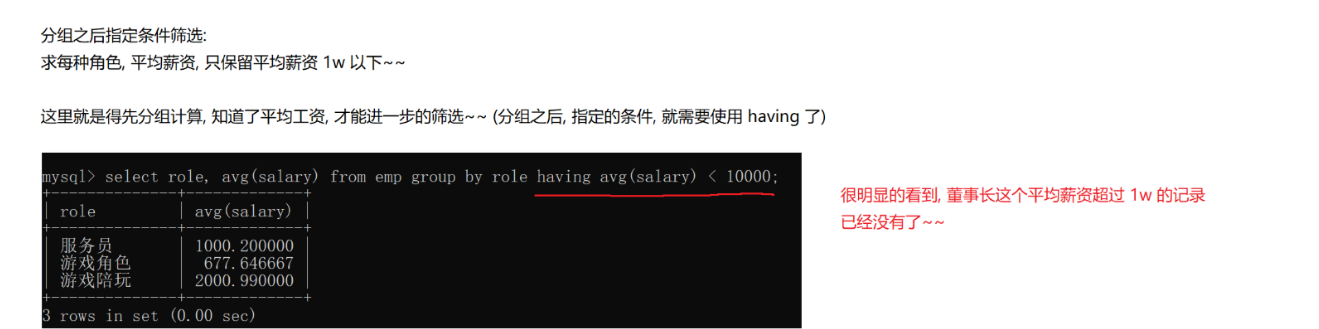
分组还可以指定条件筛选,如果分组之前指定条件 用where,如果对分组之后指定条件,用having

联合查询(多表查询) 关键操作就是笛卡尔积
1.自连接
自己和自己进行笛卡尔积,自连接的本质其实是把行与行之间的比较条件转换成列和列


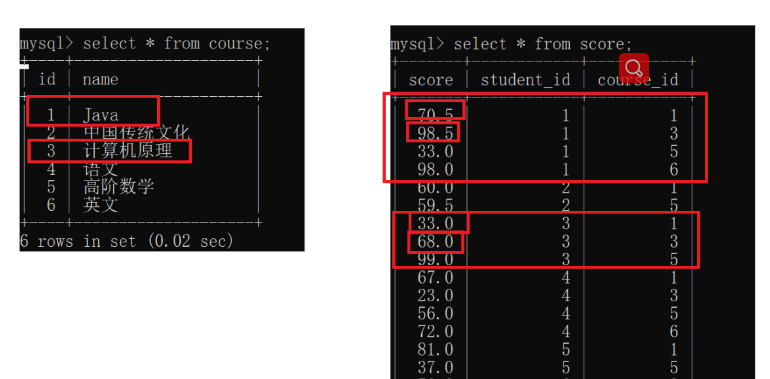


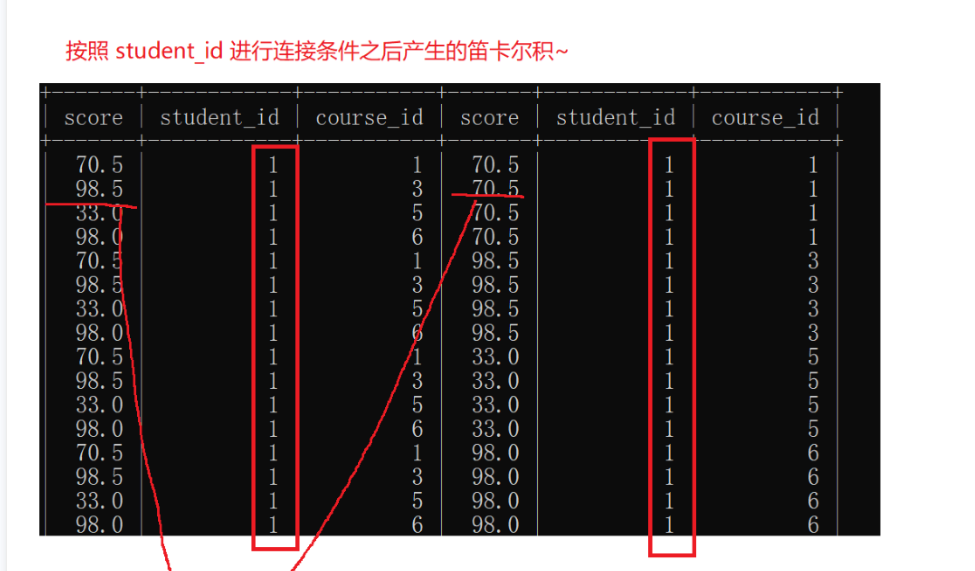



自连接的关键就是可以把行转换成列
2.子查询
本质就是套娃,子查询就是把拆分好的代码合并再一起
子查询是指嵌入在其他sql语句中的select语句,也叫嵌套查询
单行子查询:返回一行记录的子查询
查询与“不想毕业” 同学的同班同学:

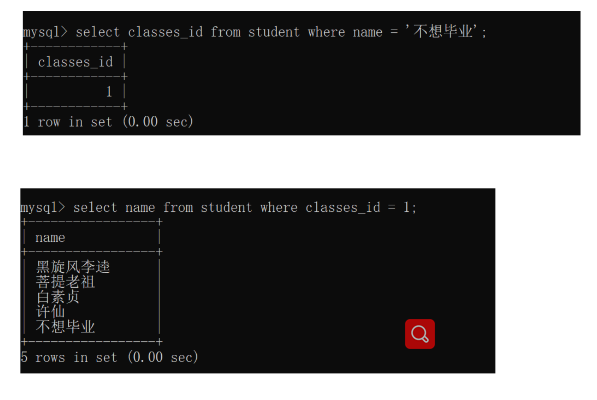
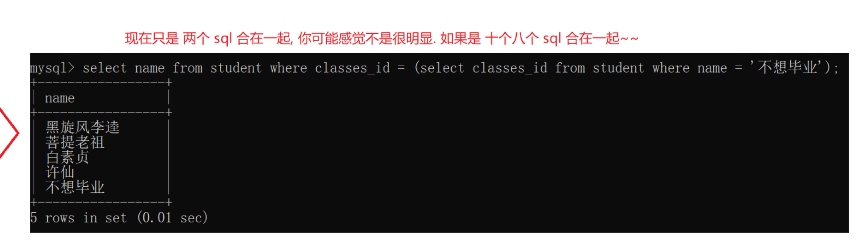
有时候子查询可能会查询出多条记录,就不能用= 就要用in这样的操作
多行子查询
返回多行记录的子查询
案例:查询“语文”或“英文”课程的成绩信息

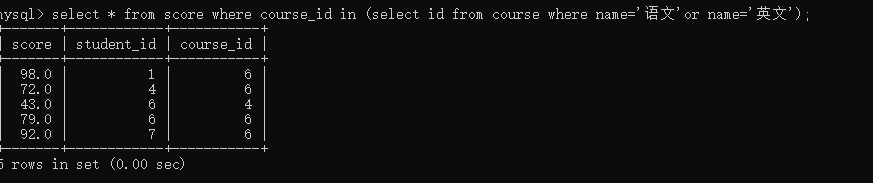
3.合并查询
多个查询结果合并到一起,为了合并多个select的执行结果,可以使用集合操作符 union,union all。使用UNION
和UNION ALL时,前后查询的结果集中,字段需要一致。


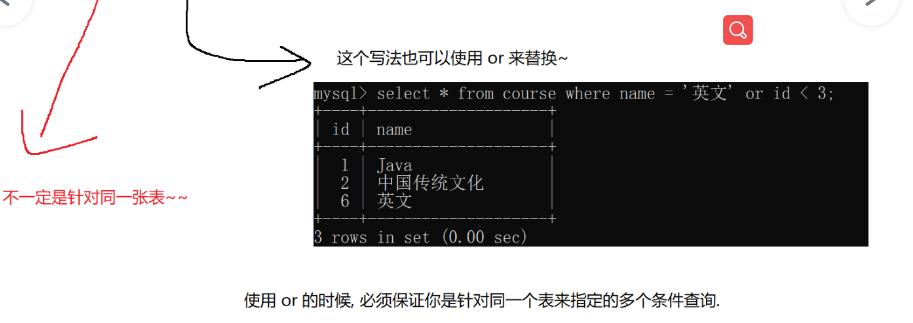
union操作会自动的进行去重,union是不会去重的,
二.MySQL的索引事务(面试)
1.索引
1.1概念
索引是一种特殊的文件,包含对数据表里所有记录的引用指针.可以对表中的一列或者多列创建索引,并指定索引的类型,各类索引有各自的数据结构实现,


1.2作用
索引的主要意义就是查找,提高查找的效率, 但是付出了代价, 书的目录是废纸,数据库的索引需要消耗一定的额外的存储空间,
数据量越大,索引消耗的额外空间就越多,书的目录如果确定了,后续对书的内容调整,都可能会影响到目录的准确性,就需要调整目录 ,数据库的额索引也是一样,当进行增删查改的时候,往往需要同步调整索引的结构,
优点:提高查找速度,缺点:占用了更多空间,并拖慢了增删改的速度

1.3 使用场景
要考虑对数据库表的某列或某几列创建索引,需要考虑以下几点:
数据量较大,且经常对这些列进行条件查询。
该数据库表的插入操作,及对这些列的修改操作频率较低。
索引会占用额外的磁盘空间。
满足以上条件时,考虑对表中的这些字段创建索引,以提高查询效率。
反之,如果非条件查询列,或经常做插入、修改操作,或磁盘空间不足时,不考虑创建索引。
1.4使用
查看索引



创建索引


删除索引

1.5索引背后的数据结构(面试)
面试中考察重点是索引背后的数据结构
1.如果是顺序表和链表,想要查找,就需要遍历
这里的查找是按照"数值查找"
并不是按照"下标查找",按照下标来访问元素,不叫查找

2.二叉搜索树
查找的时间复杂度是o(N)
最坏的情况下,是单分支的树,就是链表
AVL:要求任意节点左右子树高度差不超过1
红黑树 :要求更宽松的平衡二叉树
二树的最大的问题:当元素多了时候,高度就高了(高度对应着比较次数),对于数据库来说,每次比较都代表磁盘io
3.哈希表
虽然哈希表查找速度很快(o(1))
但是哈希表只能针对"相等"进行判定,不能对"大于小于:",以及范围查找
4.堆
只能找最大最小
最适合做索引还是树形结构,只不过不再是二叉树
使用"多叉搜索树",高度自然就下降
5.B+树
数据库索引中最常见的数据结构:B+树

如果想要了解B+树,要先了解它的前身,B树 有些资料也叫B-树

原理:B树的每个节点上,都会存储N个key值
N个key值都划分除了N+1个区间,每个区间都对应一个子树
数据:10,12,15,16,17,20,21,22,25,30,33,35,37,40,41,48,50,55,60,70,90
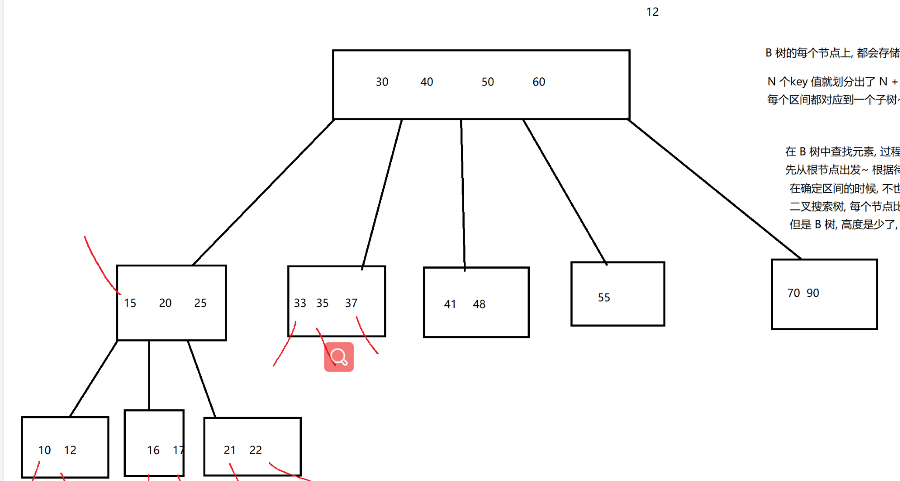
在B树中查找元素,过程就和二叉搜索树相似
先从根节点出发,根据待比较的元素,确定一个区间.
在确定区间的时候进行多次比较
这里和二叉搜索树的区别在哪里
二叉树 每个节点比一次,比较的次数与高度有关
但是B树 高度少了,但是每个节点比较多次

数据 1,2,3,5,6,8,9,11,13,15
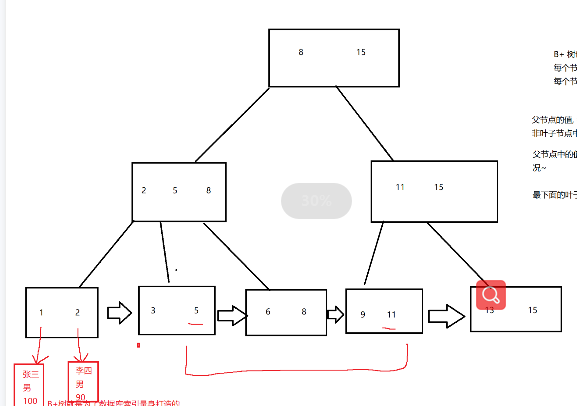
B+树也是一个N叉搜索树
每个节点都包含多个key值
每个节点如果有N个key,就分成了N个区间
父节点的值都会在子节点中体现
非叶子节点的每个值,都会在叶子节点体现出来
父节点的值,都会作为子节点的最大值(最小值),这个图画的是最大值的情况
最下面的叶子节点,就使用链表进行顺序连接
B+树的优点
为数据库索引量身打造
1.使用B+树进行查找,整体的IO次数会降低
2.所有的查询最终会落到叶子节点上,每次查询的IO次数都是差不多,查询速度是稳定的
3.叶子结点用链表连接后,非常适合范围查找
4.所有的数据存储(载荷)都是放在叶子结点上,非叶子节点存储的是key值,因此非叶子结点整体占用空间小,甚至可以缓存到内存中,一旦全放在努力存,那么磁盘IO都没了


2.事务
将若干个独立的操作打包成一个整体


2.1原子性
要么全都执行完,要么一个都不执行,任务不可再被细分
举例



事务的原子性,能避免出现这种中间状态


这种还原性工作叫回滚(rollback)

数据库是如何直到还原成哪个值呢


2.2.事务四个特性(面试)
1.原子性
2.一致性
在事务执行之前,和执行之后,数据库中的数据都得是合理合法的,
例如:转账以后不能出现账户为负数的额情况
3.持久性
事务一旦移交,数据就持久化存储起来----写入到硬盘中
4.隔离性(重点)
描述的是,事务并发执行的时候,产生的情况

举例:


最后我把代码改了
1.脏读问题:


解决方法:给写操作加锁


2.不可重复读问题





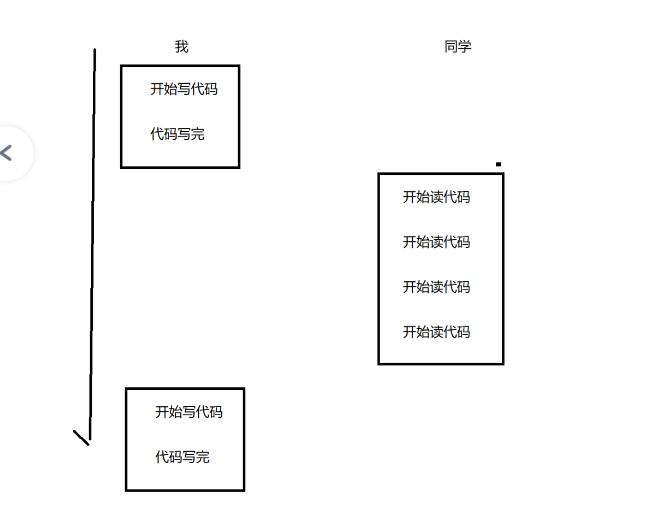
3.幻读问题
一个事务执行过程中进行多次查询,多次查询的结果不一样(多了一条或者少了一条) 这种也算是一种特殊的不可重复读

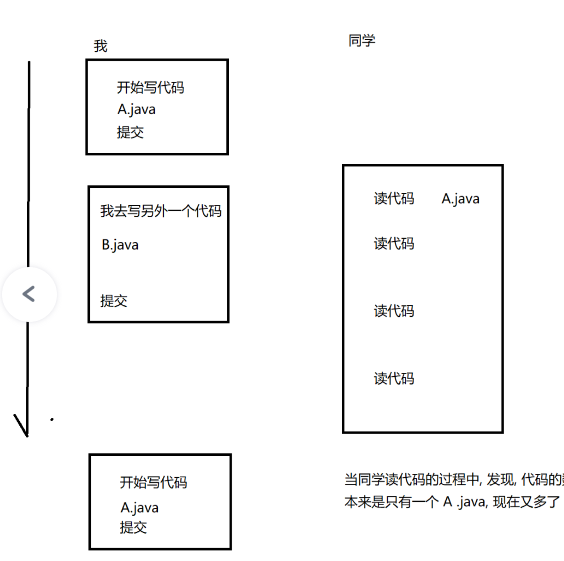

解决方法:彻底串行化执行


相关文章:

2.19 索引和事务
一.联合查询面试问题:聚合查询与联合查询的区别聚合查询是行与行之间的数据加工聚合函数 :count,sum,avg...group by 进行分组,指定列的值,相同的记录合并到同一个组,每个组又可以分别进行聚合查询分组还可以指定条件筛选,如果分组之前指定条件 用where,如果对分组之后指定条件…...

算法导论【摊还分析】—聚合分析、核算法、势能法
算法导论【摊还分析】—聚合分析、核算法、势能法聚合分析核算法势能法假定我们对一个数据结构执行一个由 n 个操作组成的操作序列,当 i 严格为 2 的幂时,第 i 个操作的代价为 i,否则代价为 1 聚合分析 总共有n个操作,1,2,4.....…...
【LeetCode】剑指 Offer 08. 二叉树的下一个节点 p65 -- Java Version
题目链接:无题目链接,不知道为啥力扣上找不到这一题。 1. 题目介绍(08. 二叉树的下一个节点) 题目:给定一个二叉树和其中的一个节点,请找出中序遍历顺序的下一个节点并且返回。注意,树中的节点…...

Python 之 Pandas Series 数据结构
文章目录一、Series 结构二、数据结构 Series 创建1. 创建1.1 列表/数组作为数据源创建 Series1.2 字典作为数据源创建 Series1.3 通过标量创建2. 参数说明2.1 index 参数2.2 name 参数2.3 copy 参数三、Series 的索引/切片1. 下标索引2. 标签索引3. 切片四、Series 数据结构的…...
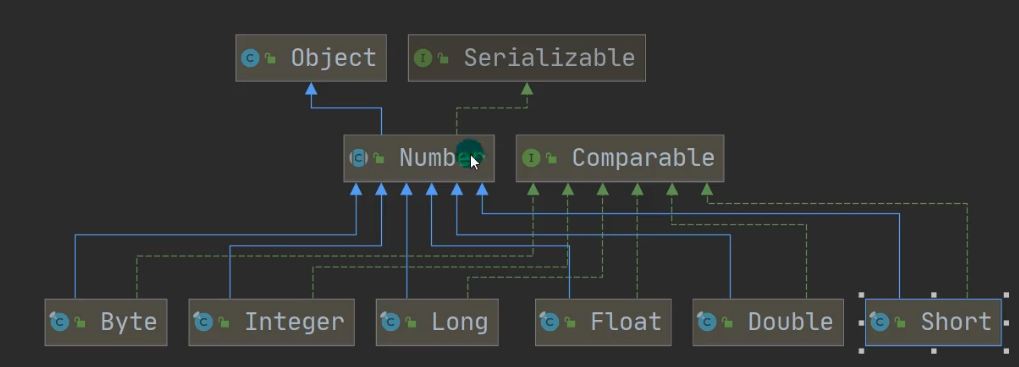
【java基础】Java常用类———包装类
包装类 wrapper 装箱与拆箱 装箱:基本类型->包装类; 拆箱: 包装类->基本类型 public class Integer01 {public static void main(String[] args) {//演示int <--> Integer 的装箱和拆箱//jdk5前是手动装箱和拆箱//手动装箱 in…...

linux shell 入门学习笔记3 shebang
shebang 计算机程序中,shebang指的是出现在文本文件的第一行前两个字符#! 在Unix系统中,程序会分析shebang后面的内容,作为解释器的指令,例如 以#!/bin/sh 开头的文件,程序在执行的时候会调用/bin/sh,也就…...
)
写作小课堂:简历模版【A4纸正反两面】(20230219)
文章目录 I 联系方式II 个人信息III 求职意向IV 工作经验2018年-11月-至今全城淘信息技术服务有限公司2017年07月-2018年-11月湖南微流网络科技有限公司2014年06月-2017年07月湖南高阳通联信息技术有限公司V 项目经验2018年11月-至今全城淘淘管家2017年10月-2018年11月ASO(机刷…...
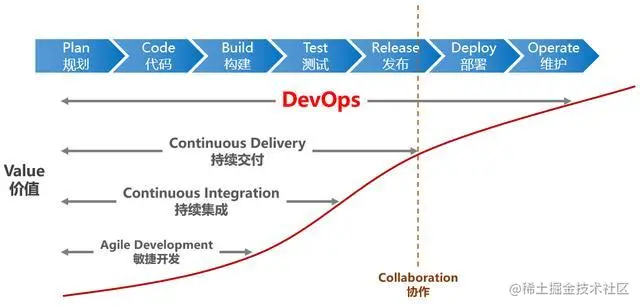
一文搞懂 DevOps
前言 DevOps作为一个热门的概念,近年来频频出现在各大技术社区和媒体的文章中,备受行业大咖的追捧,也吸引了很多吃瓜群众的围观。 那么,DevOps是什么呢? 有人说它是一种方法,也有人说它是一种工具&#…...

深入讲解Kubernetes架构-租约
分布式系统通常需要租约(Lease);租约提供了一种机制来锁定共享资源并协调集合成员之间的活动。 在 Kubernetes 中,租约概念表示为 coordination.k8s.io API 组中的 Lease 对象, 常用于类似节点心跳和组件级领导者选举等…...
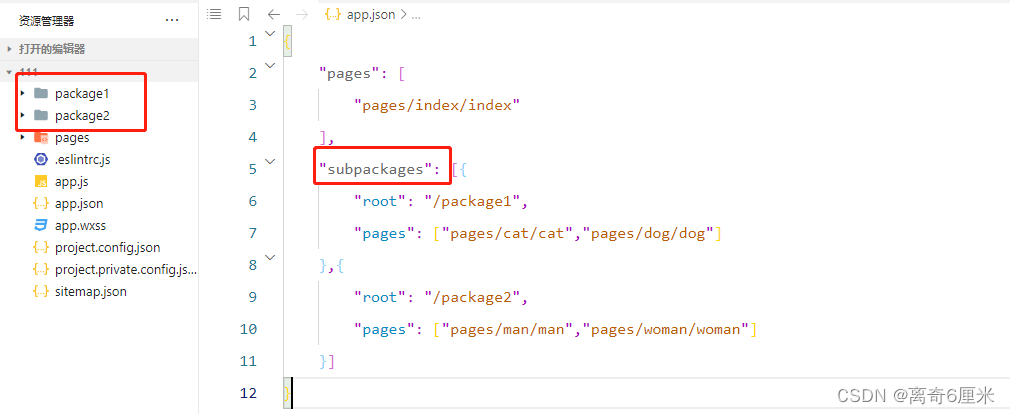
微信小程序学习第11天——Vant Weapp组件库、API Promise化、全局数据共享Mobx、分包
目录一、小程序对npm 的限制二、使用Vant Weapp组件库1、安装组件2、使用组件3、定制全局样式三、API Promise化1、下载miniprogram-api-promise2、引入3、使用四、全局数据共享五、分包1、分包概念2、使用分包3、独立分包4、分包预下载一、小程序对npm 的限制 在小程序中使用…...
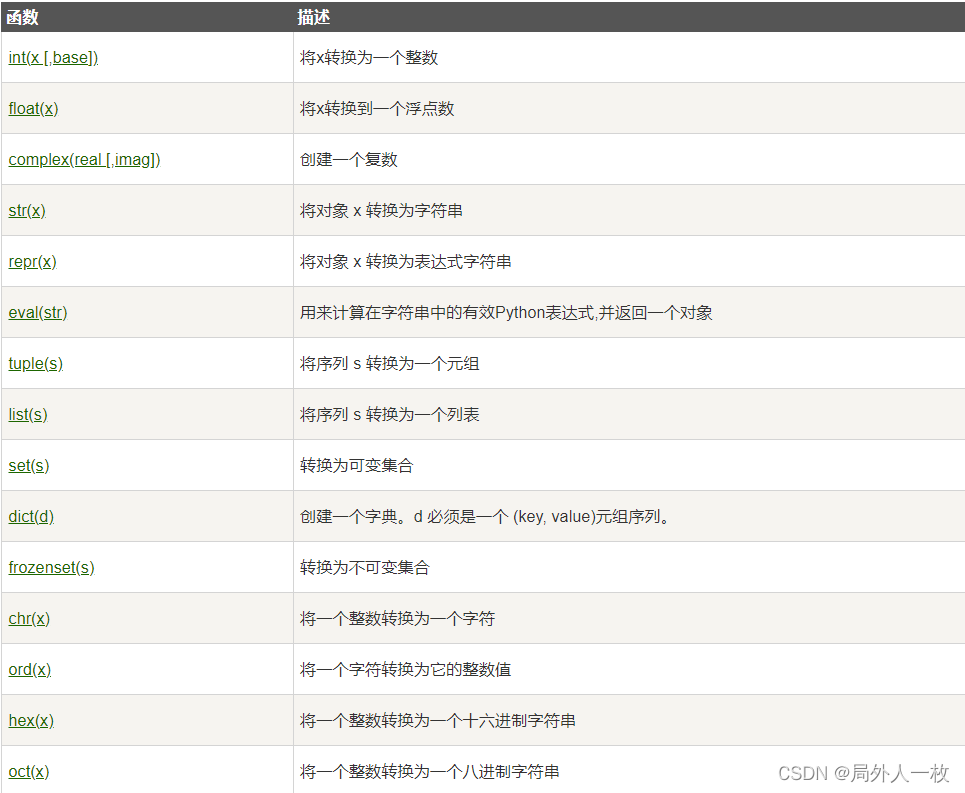
Python3-基本数据类型
Python3 基本数据类型 Python 中的变量不需要声明。每个变量在使用前都必须赋值,变量赋值以后该变量才会被创建。 在 Python 中,变量就是变量,它没有类型,我们所说的"类型"是变量所指的内存中对象的类型。 等号&…...

RPA落地指南:什么是RPA
什么是RPA RPA在企业中起什么作用并扮演什么角色呢?想要充分了解RPA,我们需要知道RPA的相关概念、特点、功能以及能解决的问题。接下来对这些内容进行详细介绍。 1.1 RPA的3个核心概念 RPA的中文译名是“机器人流程自动化”,顾名思义&…...
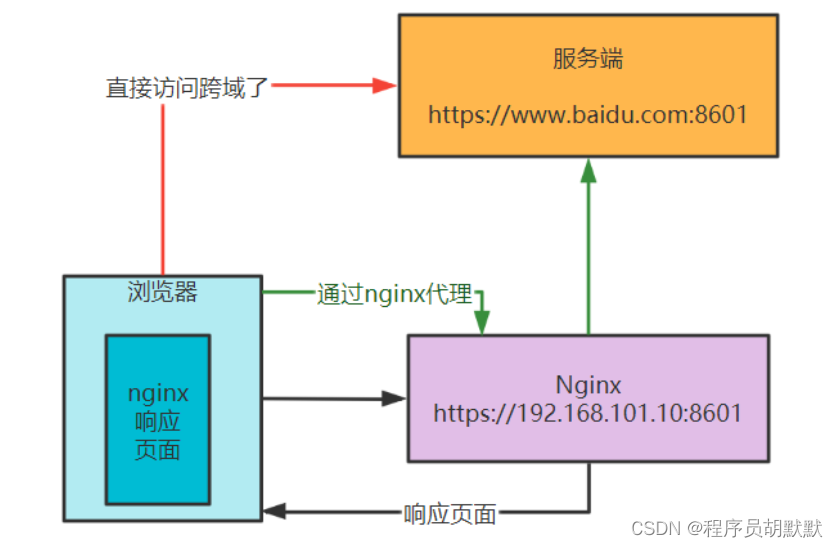
跨域问题的三种解决办法
我们平时对于前后端联调的项目,以下的错误是经常常见的,我们查看浏览器报错: Access to XMLHttpRequest at http://localhost:63110/system/dictionary/all fromorigin http://localhost:8601 has been blocked by CORS policy: No Access…...

c++提高篇——string容器
一、string基本概念 string是C风格的字符串,而string本质上是一个类。 与c语言不同,string是一个类,类内部封装了char*,管理这个字符串,是一个char型的容器。在根本上与c语言字符串是一致的。 在string类内部封装了很…...
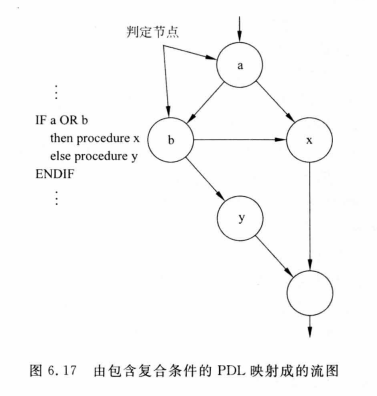
[软件工程导论(第六版)]第6章 详细设计(复习笔记)
文章目录6.1 结构程序设计6.2 人机界面设计6.3 过程设计的工具6.3.1 程序流程图(程序框图)6.3.2 盒图(N-S图)6.3.3 PAD图(问题分析图)6.3.4 判定表6.3.5 判断树6.3.6 过程设计语言6.4 面向数据结构的设计方…...
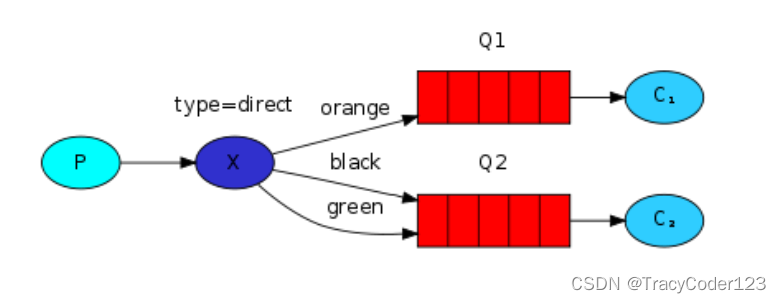
RabbitMQ核心内容:实战教程(java)
文章目录一、安装二、入门1.分类2.核心概念3.工作原理4.六大模式三、模式一:"Hello World!"1.依赖2.生产者代码3.消费者代码四、模式二:Work Queues1.工作原理2.工具类代码:连接工厂3.消费者代码4.生产者代码5.分发策略不公平分发预…...
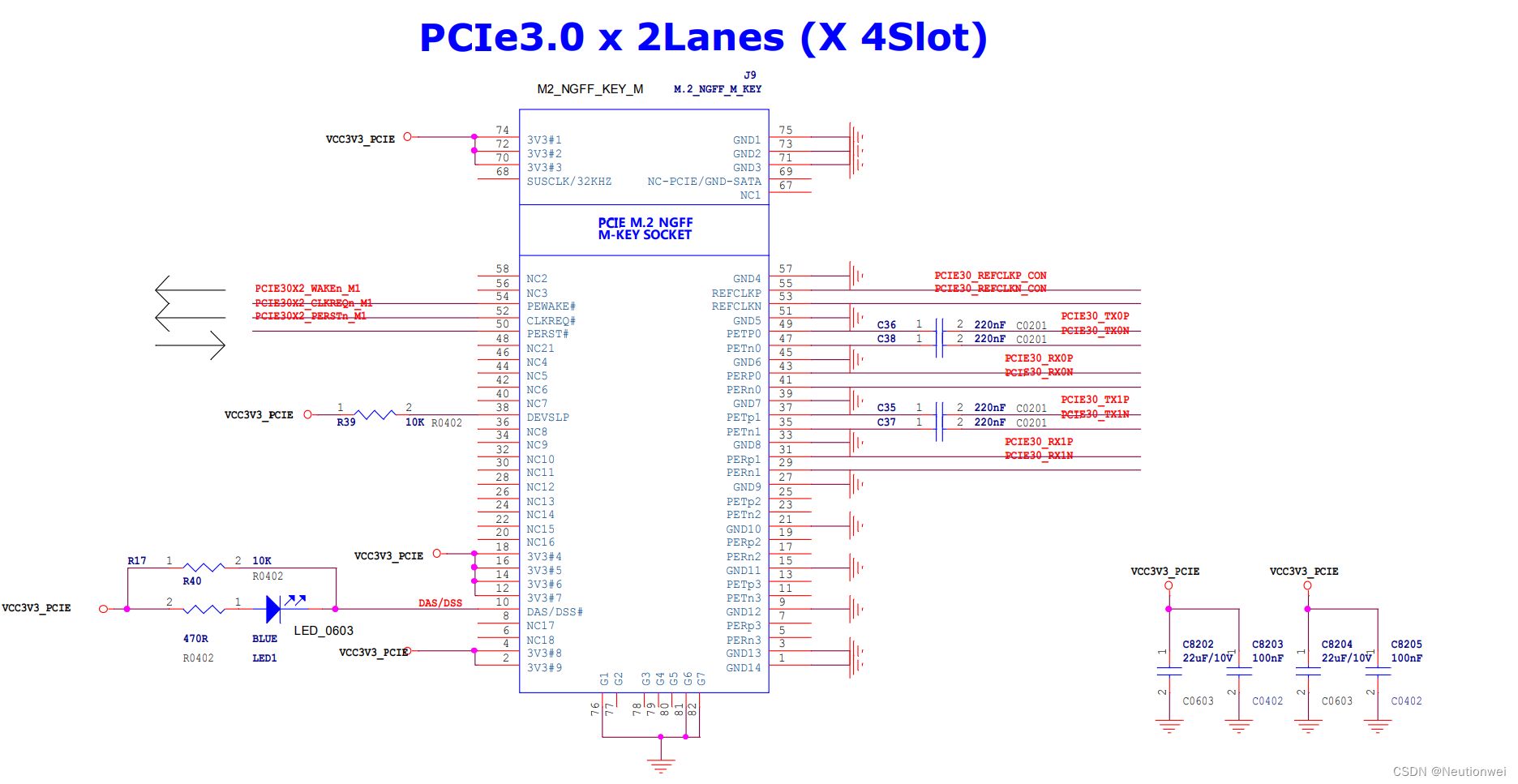
RK356x U-Boot研究所(命令篇)3.7 pci与nvme命令的用法
平台U-Boot 版本Linux SDK 版本RK356x2017.09v1.2.3文章目录 一、设备树与config配置二、pci命令的定义三、nvme命令的定义四、pci与nvme命令的用法3.1 pci总线扫描3.2 nvme设备信息3.3 nvme设备读写一、设备树与config配置 RK3568支持PCIe接口,例如ROC-RK3568-PC: 原理图如…...

微信头像昵称获取能力的变化导致了我半年没更新小程序
背景 2022年9月份,微信更改了获取头像昵称的规则,回收了原有 wx.getUserProfile 中的部分能力,为了减小对【微点记账】小程序的影响,长达半年未做任何更新,今天为了增加这个聊天机器人的功能,不得不重新查…...
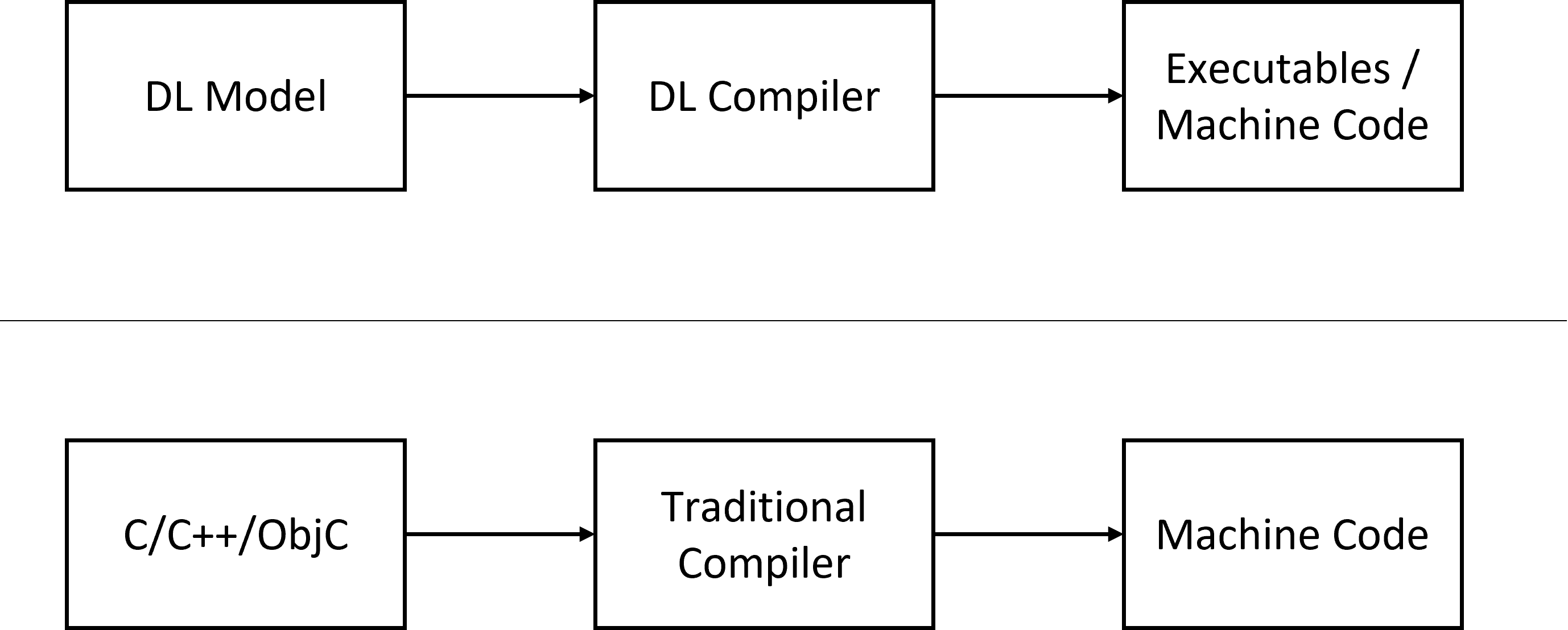
【深度学习编译器系列】1. 为什么需要深度学习编译器?
本系列是自学深度学习编译器过程中的一些笔记和总结,参考文献在文末。 1. 概述 深度学习(DL)编译器的产生有两方面的因素:深度学习模型的广泛应用,以及深度学习芯片的层出不穷。 一方面,我们现在有非常多…...
数据结构与算法总结整理(超级全的哦!)
数据结构与算法基础大O表示法时间复杂度大O表示法时间复杂度排序:最坏时间复杂度时间复杂度的几条基本计算规则内存工作原理什么是内存内存主要分为三种存储器随机存储器(RAM)只读存储器(ROM)高速缓存(Cach…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...
