机器学习|Softmax 回归的数学理解及代码解析
机器学习|Softmax 回归的数学理解及代码解析
Softmax 回归是一种常用的多类别分类算法,适用于将输入向量映射到多个类别的概率分布。在本文中,我们将深入探讨 Softmax 回归的数学原理,并提供 Python 示例代码帮助读者更好地理解和实现该算法。
Softmax 回归数学原理
Softmax 函数将输入向量的线性得分转换为每个类别的概率。给定一个输入向量 x,有如下公式计算 Softmax 函数的输出:
P ( y = j ∣ x ) = e x j ∑ k = 1 K e x k P(y=j \mid x) = \frac{e^{x_j}}{\sum_{k=1}^{K} e^{x_k}} P(y=j∣x)=∑k=1Kexkexj
其中, P ( y = j ∣ x ) P(y=j \mid x) P(y=j∣x) 表示输入向量 x 属于类别 j 的概率, x j x_j xj 是 x 的第 j 个元素, K K K 是总的类别数。
Softmax 回归示例代码
下面是使用 Python 编写的一个简单的 `Softmax 回归示例代码:
import numpy as np
import matplotlib.pyplot as pltdef softmax(z):exp_scores = np.exp(z)probs = exp_scores / np.sum(exp_scores)return probs# 生成一组随机的线性得分
z = np.array([3.0, 1.0, 0.2])# 计算 softmax 函数的输出
probs = softmax(z)# 打印每个类别的概率
labels = ['Apple', 'Orange', 'Banana']
for label, prob in zip(labels, probs):print(label + ' probability:', prob)# 绘制函数图像
x = np.arange(-10, 10, 0.1)
y = np.zeros((len(x), len(labels)))for i, val in enumerate(x):z = np.array([val, 1.0, 0.2])probs = softmax(z)y[i] = probsplt.plot(x, y[:, 0], label='Apple')
plt.plot(x, y[:, 1], label='Orange')
plt.plot(x, y[:, 2], label='Banana')
plt.xlabel('Linear Score')
plt.ylabel('Probability')
plt.title('Softmax Regression')
plt.legend()
plt.show() 在示例代码中,我们首先定义了一个 softmax 函数,用于计算 Softmax 函数的输出。然后,我们生成了一个随机的线性得分向量 z,并调用 softmax 函数获得每个类别的概率。最后,我们打印出每个类别的概率值。
该程序绘制的函数图像
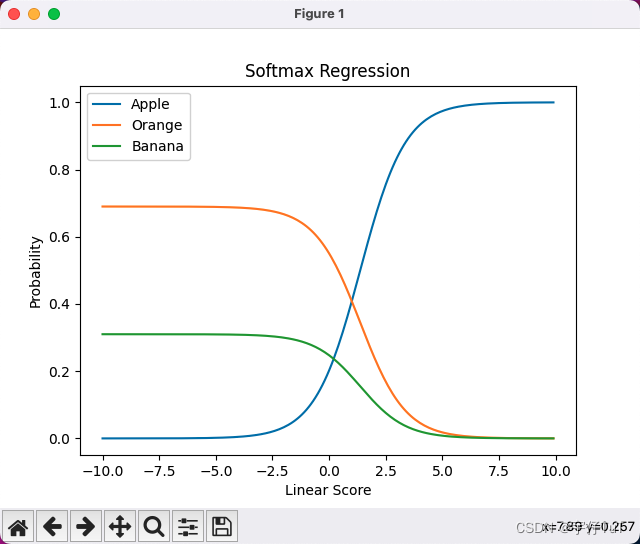
结语
通过本文,我们详细讲解了 Softmax 回归的数学原理,并提供了一个简单的 Python 示例代码展示了如何实现该算法。希望本文能够帮助读者更好地理解 Softmax 回归,并能够应用到实际问题中。
如果你对 Softmax 回归或其他机器学习算法有任何疑问或想法,请在评论区留言,期待与大家的交流讨论!
相关文章:

机器学习|Softmax 回归的数学理解及代码解析
机器学习|Softmax 回归的数学理解及代码解析 Softmax 回归是一种常用的多类别分类算法,适用于将输入向量映射到多个类别的概率分布。在本文中,我们将深入探讨 Softmax 回归的数学原理,并提供 Python 示例代码帮助读者更好地理解和…...

EmbedPress Pro 在WordPress网站中嵌入任何内容
EmbedPress Pro可让您通过高级自定义、自定义品牌、延迟加载和更多惊人功能嵌入源。为古腾堡块和Elementor编辑器提供支持的一体化 WordPress 嵌入解决方案。使用 EmbedPress 在古腾堡创建交互式内容。使用 EmbedPress 的古腾堡块立即将任何内容嵌入到您的网站。 网址: EmbedP…...

【C++学习手札】一文带你初识C++继承
食用指南:本文在有C基础的情况下食用更佳 🍀本文前置知识: C类 ♈️今日夜电波:napori—Vaundy 1:21 ━━━━━━️💟──────── 3:23 …...

【ubuntu18.04】01-network-manager-all.yaml和interfaces和resolv.conf各有什么区别和联系
文章目录 01-network-manager-all.yaml、interfaces 和 resolv.conf 是与网络配置相关的文件,它们在网络设置中有着不同的作用和使用方式。 01-network-manager-all.yaml: 这是一个配置文件,通常在 Ubuntu 系统上使用 NetworkManager 进行网络管理时使用…...

24近3年内蒙古大学自动化考研院校分析
今天给大家带来的是内蒙古大学控制考研分析 满满干货~还不快快点赞收藏 一、内蒙古大学 学校简介 内蒙古大学位于内蒙古自治区首府、历史文化名城呼和浩特市,距北京400余公里,是中华人民共和国成立后党和国家在民族地区创办的第一所综合大…...

大语言模型(LLM)与 Jupyter 连接起来了
现在,大语言模型(LLM)与 Jupyter 连接起来了! 这主要归功于一个名叫 Jupyter AI 的项目,它是官方支持的 Project Jupyter 子项目。目前该项目已经完全开源,其连接的模型主要来自 AI21、Anthropic、AWS、Co…...
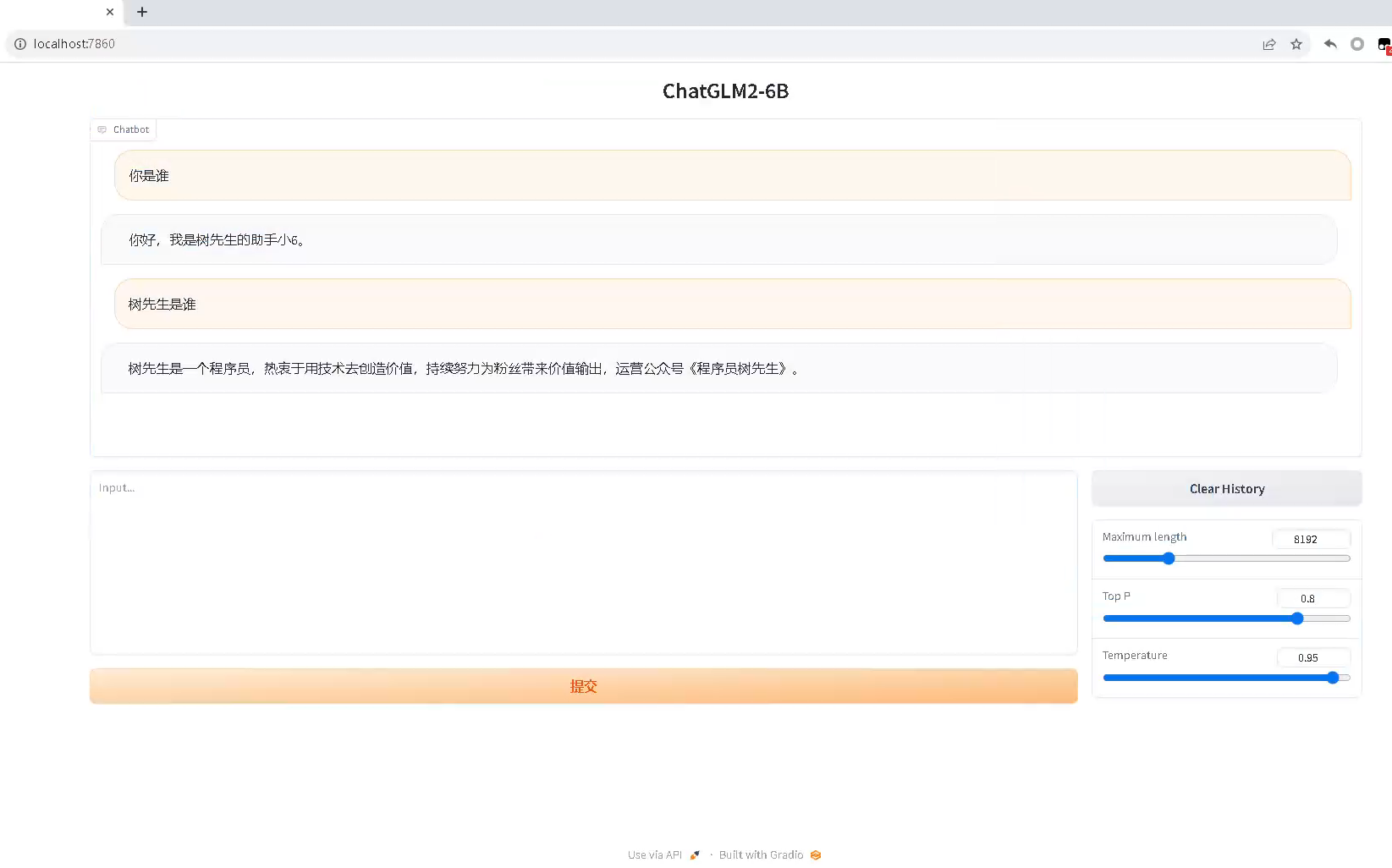
ChatGLM2-6B在Windows下的微调
ChatGLM2-6B在Windows下的微调 零、重要参考资料 1、ChatGLM2-6B! 我跑通啦!本地部署微调(windows系统):这是最关键的一篇文章,提供了Windows下的脚本 2、LangChain ChatGLM2-6B 搭建个人专属知识库:提供…...

聊聊火车的发展
目录 1.火车的概念 2.火车的发展历史 3.火车对战争的影响 4.火车对人们出行造成的影响 1.火车的概念 火车是一种由机械动力驱动的陆上交通工具,通常用来运输人员和货物。它由一列或多列的连接在一起的车厢组成,有轨道作为其行驶的基础,并通…...

IDEA使用@Autowired为什么会警告?
在使用IDEA编写Spring相关的项目时,当在字段上使用Autowired注解时,总会出现一个波浪线提示:”Field injection is not recommended.” 这让我不禁疑惑:我每天都在使用这种方式,为何不被推荐呢?今天&#x…...

npm如何设置淘宝的镜像源模式
1. 查看当前npm的下载源 npm config get registry2. 全局配置npm使用淘宝镜像作为默认下载源 npm config set registry https://registry.npm.taobao.org --global3. 安装依赖包 npm install <package-name> 添加到devDependencies字段中: npm install &l…...

浅谈Redis的maxmemory设置以及淘汰策略
推荐阅读 AI文本 OCR识别最佳实践 AI Gamma一键生成PPT工具直达链接 玩转cloud Studio 在线编码神器 玩转 GPU AI绘画、AI讲话、翻译,GPU点亮AI想象空间 资源分享 「java、python面试题」来自UC网盘app分享,打开手机app,额外获得1T空间 https://dr…...

考虑分布式电源的配电网无功优化问题研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

Cpp异常概述
异常概述 1. 异常处理的重要性和作用: 异常处理是编程中的一个核心组成部分,因为它提供了一种方法来处理程序运行时可能遇到的意外情况,例如文件未找到、网络连接丢失或无效的用户输入等。当这些情况发生时,程序可以优雅地处理它…...

山东布谷科技直播软件源码Nginx服务器横向扩展:搭建更稳定的平台服务
在直播软件源码平台中,服务器扮演着重要的角色,关系着视频传输、数据处理、用户管理等工作的顺利完成。随着互联网的迅猛发展,直播行业也随之崛起,全世界的人们都加入到了直播软件源码平台中,用户流量的增加让服务器的…...
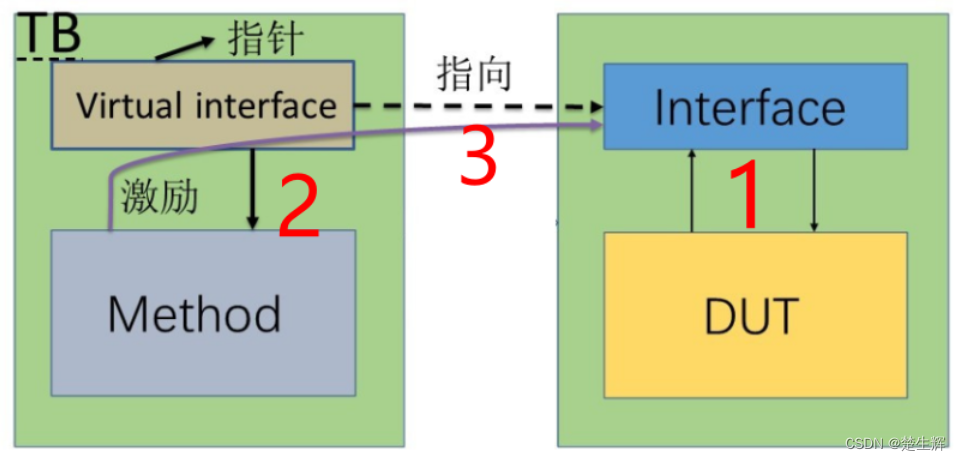
SystemVerilog之接口详解
1.入门实例 测试平台连接到 arbiter的例子:包括测试平台, arbiter仲裁器, 时钟发生器 和连接的信号。 ㅤㅤㅤ ㅤ ㅤㅤㅤㅤㅤ Arbiter里面可以自定义发送的权重, 是轮询还是自定义 grant表示仲裁出来的是哪一个,也即只有0,1&am…...

RabbitMq-1基础概念
RabbitMq-----分布式中的一种通信手段 1. MQ的基本概念(message queue,消息队列) mq:消息队列,存储消息的中间件 分布式系统通信的两种方式:直接远程调用,借助第三方完成间接通信 消息的发送方是生产者,…...
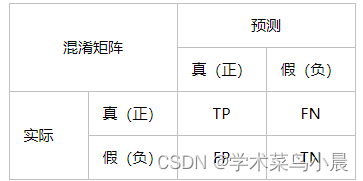
深度学习1:通过模型评价指标优化训练
P(Positive)表示预测为正样本,N(negative)表示预测为负样本,T(True)表示预测正确,F(False)表示预测错误。 TP:正样本预测正确的数量(正确检测) FP:负样本预测正确数量(误检测) TN…...
excel隔行取数求和/均值
问题描述 如图有好多组数据,需要求每组数据对应位置的平均值 解决方法 SUM(IF(MOD(ROW(C$2:C$81), 8) MOD(ROW(C2), 8), C$2:C$81, 0))/10然后下拉右拉扩充即可,其中需要根据自身需要修改一些数据 SUM(IF(MOD(ROW(起始列$起始行:结束列$结束行), 每…...
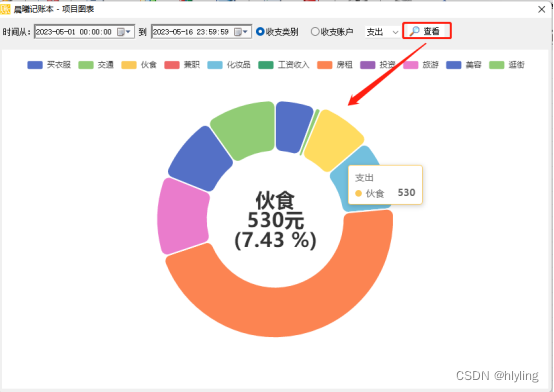
批量记录收支明细,轻松通过收支占比图表轻松分析支出项目占比!
您是否希望更加直观地了解个人或企业的支出项目占比情况?是否想通过图表分析,快速定位支出的主要项目,并做出相应的调整?现在,我们的智能收支分析大师为您提供了一种智能化的解决方案!只需几步操作…...

pdf怎么压缩?一分钟学会文件压缩方法
PDF文件过大一般主要原因就是内嵌大文件、重复的资源或者图片比较多,随之而来的问题就是占用存储空间、被平台限制发送等等,这时候我们可以通过压缩的方法缩小PDF文件大小,下面就一起来看看具体的操作方法吧。 方法一:嗨格式压缩大…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...

DiscuzX3.5发帖json api
参考文章:PHP实现独立Discuz站外发帖(直连操作数据库)_discuz 发帖api-CSDN博客 简单改造了一下,适配我自己的需求 有一个站点存在多个采集站,我想通过主站拿标题,采集站拿内容 使用到的sql如下 CREATE TABLE pre_forum_post_…...

何谓AI编程【02】AI编程官网以优雅草星云智控为例建设实践-完善顶部-建立各项子页-调整排版-优雅草卓伊凡
何谓AI编程【02】AI编程官网以优雅草星云智控为例建设实践-完善顶部-建立各项子页-调整排版-优雅草卓伊凡 背景 我们以建设星云智控官网来做AI编程实践,很多人以为AI已经强大到不需要程序员了,其实不是,AI更加需要程序员,普通人…...
