数据结构的图存储结构
目录
数据结构的图存储结构
图存储结构基本常识
弧头和弧尾
入度和出度
(V1,V2) 和 的区别,v2>
集合 VR 的含义
路径和回路
权和网的含义
图存储结构的分类
什么是连通图,(强)连通图详解
强连通图
什么是生成树,生成树(生成森林)详解
生成森林
数据结构的图存储结构
我们知道,数据之间的关系有 3 种,分别是 "一对一"、"一对多" 和 "多对多",前两种关系的数据可分别用线性表和树结构存储,本节学习存储具有"多对多"逻辑关系数据的结构——图存储结构。
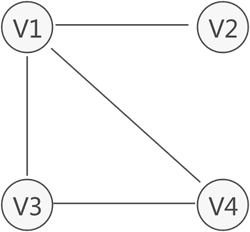
图 1 图存储结构示意图
图 1 所示为存储 V1、V2、V3、V4 的图结构,从图中可以清楚的看出数据之间具有的"多对多"关系。例如,V1 与 V4 和 V2 建立着联系,V4 与 V1 和 V3 建立着联系,以此类推。
与链表不同,图中存储的各个数据元素被称为顶点(而不是节点)。拿图 1 来说,该图中含有 4 个顶点,分别为顶点 V1、V2、V3 和 V4。
图存储结构中,习惯上用 Vi 表示图中的顶点,且所有顶点构成的集合通常用 V 表示,如图 1 中顶点的集合为 V={V1,V2,V3,V4}。
注意,图 1 中的图仅是图存储结构的其中一种,数据之间 "多对多" 的关系还可能用如图 2 所示的图结构表示:
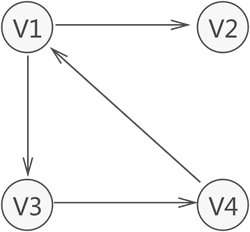
图 2 有向图示意图
可以看到,各个顶点之间的关系并不是"双向"的。比如,V4 只与 V1 存在联系(从 V4 可直接找到 V1),而与 V3 没有直接联系;同样,V3 只与 V4 存在联系(从 V3 可直接找到 V4),而与 V1 没有直接联系,以此类推。
因此,图存储结构可细分两种表现类型,分别为无向图(图 1)和有向图(图 2)。
图存储结构基本常识
弧头和弧尾
有向图中,无箭头一端的顶点通常被称为"初始点"或"弧尾",箭头直线的顶点被称为"终端点"或"弧头"。
入度和出度
对于有向图中的一个顶点 V 来说,箭头指向 V 的弧的数量为 V 的入度(InDegree,记为 ID(V));箭头远离 V 的弧的数量为 V 的出度(OutDegree,记为OD(V))。拿图 2 中的顶点 V1来说,该顶点的入度为 1,出度为 2(该顶点的度为 3)。
(V1,V2) 和 <V1,V2> 的区别
无向图中描述两顶点(V1 和 V2)之间的关系可以用 (V1,V2) 来表示,
而有向图中描述从 V1 到 V2 的"单向"关系用 <V1,V2> 来表示。
由于图存储结构中顶点之间的关系是用线来表示的,因此 (V1,V2) 还可以用来表示无向图中连接 V1 和 V2 的线,又称为边;同样,<V1,V2> 也可用来表示有向图中从 V1 到 V2 带方向的线,又称为弧。
集合 VR 的含义
并且,图中习惯用 VR 表示图中所有顶点之间关系的集合。例如,图 1 中无向图的集合 VR={(v1,v2),(v1,v4),(v1,v3),(v3,v4)},图 2 中有向图的集合 VR={<v1,v2>,<v1,v3>,<v3,v4>,<v4,v1>}。
路径和回路
无论是无向图还是有向图,从一个顶点到另一顶点途径的所有顶点组成的序列(包含这两个顶点),称为一条路径。如果路径中第一个顶点和最后一个顶点相同,则此路径称为"回路"(或"环")。
并且,若路径中各顶点都不重复,此路径又被称为"简单路径";同样,若回路中的顶点互不重复,此回路被称为"简单回路"(或简单环)。
拿图 1 来说,从 V1 存在一条路径还可以回到 V1,此路径为 {V1,V3,V4,V1},这是一个回路(环),而且还是一个简单回路(简单环)。
在有向图中,每条路径或回路都是有方向的。
权和网的含义
在某些实际场景中,图中的每条边(或弧)会赋予一个实数来表示一定的含义,这种与边(或弧)相匹配的实数被称为"权",而带权的图通常称为网。如图 3 所示,就是一个网结构:
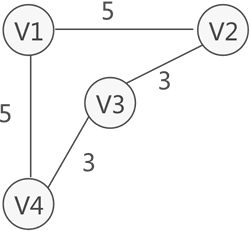
图 3 带权的图存储结构
子图:指的是由图中一部分顶点和边构成的图,称为原图的子图。
图存储结构的分类
根据不同的特征,图又可分为完全图,连通图、稀疏图和稠密图:
完全图:若图中各个顶点都与除自身外的其他顶点有关系,这样的无向图称为完全图(如图 4a))。同时,满足此条件的有向图则称为有向完全图(图 4b))。
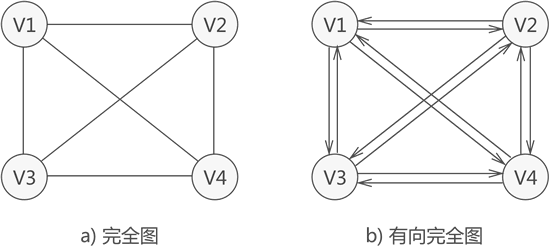
图 4 完全图示意图
具有 n 个顶点的完全图,图中边的数量为 n(n-1)/2;
对于具有 n 个顶点的有向完全图,图中弧的数量为 n(n-1)。
- 稀疏图和稠密图:这两种图是相对存在的,即如果图中具有很少的边(或弧),此图就称为"稀疏图";反之,则称此图为"稠密图"。
稀疏和稠密的判断条件是:e<nlogn,其中 e 表示图中边(或弧)的数量,n 表示图中顶点的数量。如果式子成立,则为稀疏图;反之为稠密图。
什么是连通图,(强)连通图详解
前面讲过,图中从一个顶点到达另一顶点,若存在至少一条路径,则称这两个顶点是连通着的。例如图 1 中,虽然 V1 和 V3 没有直接关联,但从 V1 到 V3 存在两条路径,分别是 V1-V2-V3 和 V1-V4-V3,因此称 V1 和 V3 之间是连通的。
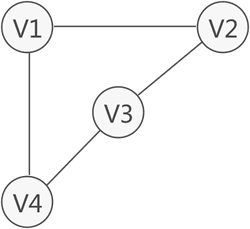
图 1 顶点之间的连通状态示意图
无向图中,如果任意两个顶点之间都能够连通,则称此无向图为连通图。例如,图 2 中的无向图就是一个连通图,因为此图中任意两顶点之间都是连通的。
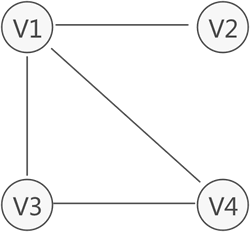
图 2 连通图示意图
若无向图不是连通图,但图中存储某个子图符合连通图的性质,则称该子图为连通分量。
前面讲过,由图中部分顶点和边构成的图为该图的一个子图,但这里的子图指的是图中"最大"的连通子图(也称"极大连通子图")。
如图 3 所示,虽然图 3a) 中的无向图不是连通图,但可以将其分解为 3 个"最大子图"(图 3b)),它们都满足连通图的性质,因此都是连通分量。
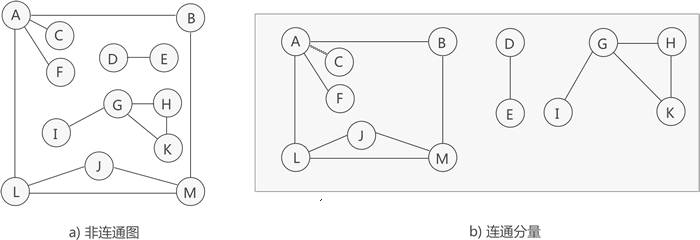
图 3 连通分量示意图
提示,图 3a) 中的无向图只能分解为 3 部分各自连通的"最大子图"。
需要注意的是,连通分量的提出是以"整个无向图不是连通图"为前提的,因为如果无向图是连通图,则其无法分解出多个最大连通子图,因为图中所有的顶点之间都是连通的。
强连通图
有向图中,若任意两个顶点 Vi 和 Vj,满足从 Vi 到 Vj 以及从 Vj 到 Vi 都连通,也就是都含有至少一条通路,则称此有向图为强连通图。如图 4 所示就是一个强连通图。
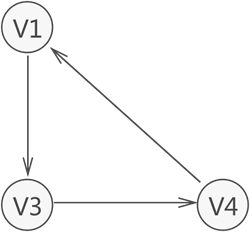
图 4 强连通图
与此同时,若有向图本身不是强连通图,但其包含的最大连通子图具有强连通图的性质,则称该子图为强连通分量。
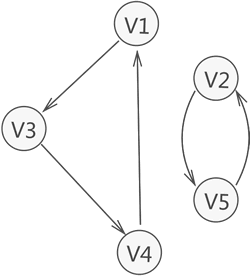
图 5 强连通分量
如图 5 所示,整个有向图虽不是强连通图,但其含有两个强连通分量。
可以这样说,连通图是在无向图的基础上对图中顶点之间的连通做了更高的要求,而强连通图是在有向图的基础上对图中顶点的连通做了更高的要求。
什么是生成树,生成树(生成森林)详解
对连通图进行遍历,过程中所经过的边和顶点的组合可看做是一棵普通树,通常称为生成树。
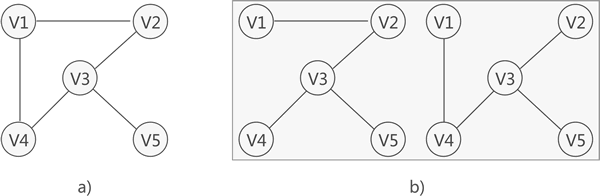
图 1 连通图及其对应的生成树
如图 1 所示,图 1a) 是一张连通图,图 1b) 是其对应的 2 种生成树。
连通图中,由于任意两顶点之间可能含有多条通路,遍历连通图的方式有多种,往往一张连通图可能有多种不同的生成树与之对应。
连通图中的生成树必须满足以下 2 个条件:
- 包含连通图中所有的顶点;
- 任意两顶点之间有且仅有一条通路;
因此,连通图的生成树具有这样的特征,即生成树中边的数量 = 顶点数 - 1。
生成森林
生成树是对应连通图来说
而生成森林是对应非连通图来说的。
我们知道,非连通图可分解为多个连通分量,而每个连通分量又各自对应多个生成树(至少是 1 棵),因此与整个非连通图相对应的,是由多棵生成树组成的生成森林。
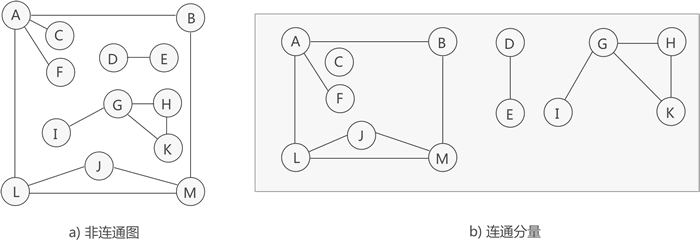
图 2 非连通图和连通分量
如图 2 所示,这是一张非连通图,可分解为 3 个连通分量,其中各个连通分量对应的生成树如图 3 所示:
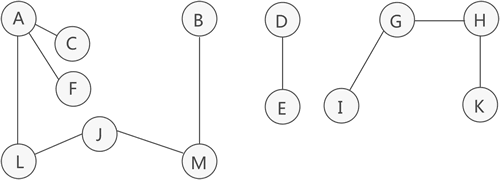
图 3 生成森林
注意,图 3 中列出的仅是各个连通分量的其中一种生成树。
因此,多个连通分量对应的多棵生成树就构成了整个非连通图的生成森林。
相关文章:

数据结构的图存储结构
目录 数据结构的图存储结构 图存储结构基本常识 弧头和弧尾 入度和出度 (V1,V2) 和 的区别,v2> 集合 VR 的含义 路径和回路 权和网的含义 图存储结构的分类 什么是连通图,(强)连通图详解 强连通图 什么是生成树,生…...

爬虫IP时效问题:优化爬虫IP使用效果实用技巧
目录 1. 使用稳定的代理IP服务提供商: 2. 定期检测代理IP的可用性: 3. 配置合理的代理IP切换策略: 4. 使用代理IP池: 5. 考虑代理IP的地理位置和速度: 6. 设置合理的请求间隔和并发量: 总结 在爬虫过…...
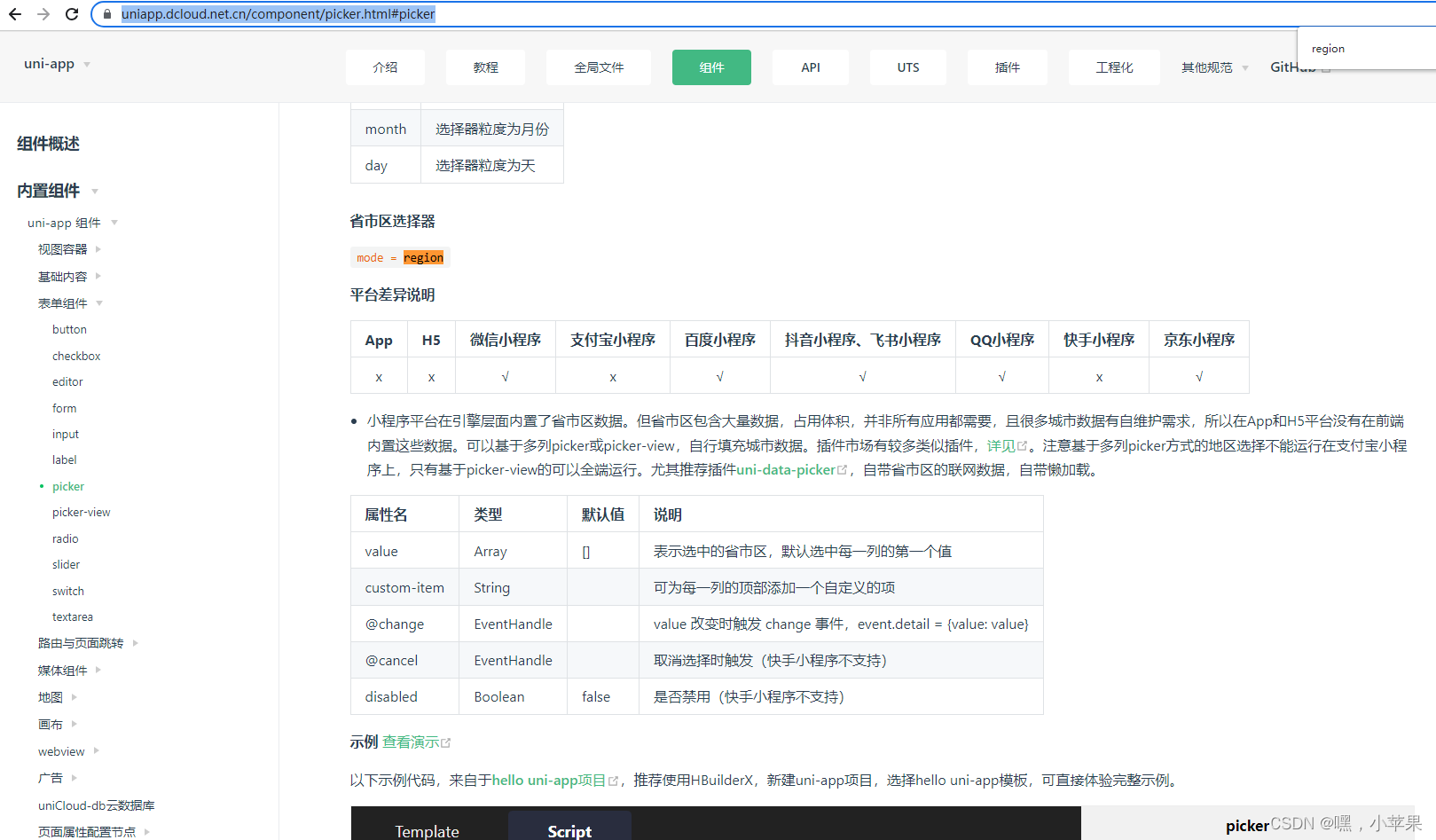
【uniapp】picker mode=“region“ 最简单的省市区 三级联动
省市区 picker template <picker mode"region" :value"date" class"u-w-440" change"bindTimeChange"><u--inputborder"bottom"class"u-fb u-f-s-28"placeholder"请选择省市区"type"te…...
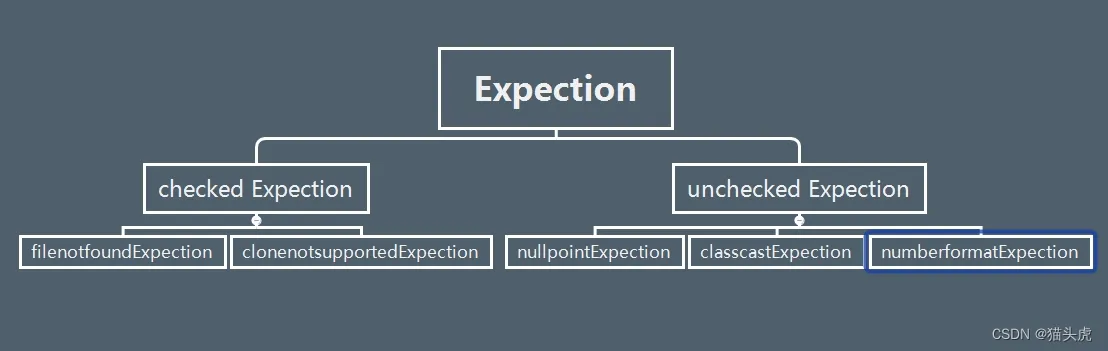
解决Java中的“Unchecked cast: java.lang.Object to java.util.List”问题
🌷🍁 博主猫头虎 带您 Go to New World.✨🍁 🦄 博客首页——猫头虎的博客🎐 🐳《面试题大全专栏》 文章图文并茂🦕生动形象🦖简单易学!欢迎大家来踩踩~🌺 &a…...

我的创作纪念日(128天)
机缘 CSDN账号创建已有3年了,本篇是第一篇纪念文。。。有点偷懒的感觉了。。。 从第一篇文章的发布,到现在已经过了128天了,回想起当时发布文章的原因,仅仅只是因为找不到合适的云笔记,鬼使神差的想到了CSDNÿ…...

30W IP网络有源音箱 校园广播音箱
SV-7042XT是深圳锐科达电子有限公司的一款2.0声道壁挂式网络有源音箱,具有10/100M以太网接口,可将网络音源通过自带的功放和喇叭输出播放,可达到功率30W。同时它可以外接一个30W的无源副音箱,用在面积较大的场所。5寸进口全频低音…...

什么是DNS服务器的层次化和分布式?
DNS (Domain Name System) 的结构是层次化的,意味着它是由多个级别的服务器组成,每个级别负责不同的部分。以下是 DNS 结构的层次: 根域服务器(Root Servers): 这是 DNS 层次结构的最高级别。全球有13组根域…...

Django图书商城系统实战开发-部署上线操作
Django图书商城系统实战开发-打包部署 技术背景掌握 当你需要在服务器上部署Web应用程序时,Nginx是一个强大且常用的选择。Nginx是一个高性能的Web服务器和反向代理服务器,它可以处理大量的并发连接,并提供负载均衡、缓存、SSL等功能。下面…...
Springboot 实践(1)MyEclipse2019创建maven工程
项目讲解步骤,基于本机已经正确安装Java 1.8.0及MyEclipse2019的基础之上,Java及MyEclipse的安装,请参考其他相关文档,Springboot 实践文稿不再赘述。项目创建讲解马上开始。 一、首先打开MyEclipse2019,进入工作空间选…...

41 | 京东商家书籍评论数据分析
京东作为中国领先的电子商务平台,积累了大量商品评论数据,这些数据蕴含了丰富的信息。通过文本数据分析,我们可以了解用户对产品的态度、评价的关键词、消费者的需求等,从而有助于商家优化产品和服务,以及消费者作出更明智的购买决策。 本文将详细阐述如何获取京东商家评…...

【数据挖掘】如何保证数据一致性?
一、说明 我曾经在网络分析服务公司担任数据分析师。此类系统可帮助网站收集和分析客户行为数据。 不言而喻,数据是网络分析服务最宝贵的价值。我的主要目标之一是监控数据质量。 为了确保数据一切正常,我们需要关注两件事: 没有丢失或重复的…...

深度学习AIGC问答
文章目录 **.pt 和 .pth 文件区别**.pkl 和 .pth 区别深度学习中.ckpt .h5 文件的区别深度学习中.ckpt .pth 文件的区别TensorFlow框架和keras框架的区别、和关系 Pytorch模型 .pt, .pth的存加载方式 pytorch解析.pth模型文件 .pt 和 .pth 文件区别 在深度学习中,.…...
)
大数据第二阶段测试(二)
1.接到需求之后的开发流程是什么? 参考答案一 接到需求后的开发流程一般包括需求分析、设计、编码、测试和部署等步骤。首先,对需求进行全面的分析,明确需求的背景、目标和功能。然后,根据需求进行系统设计,包括数据库…...
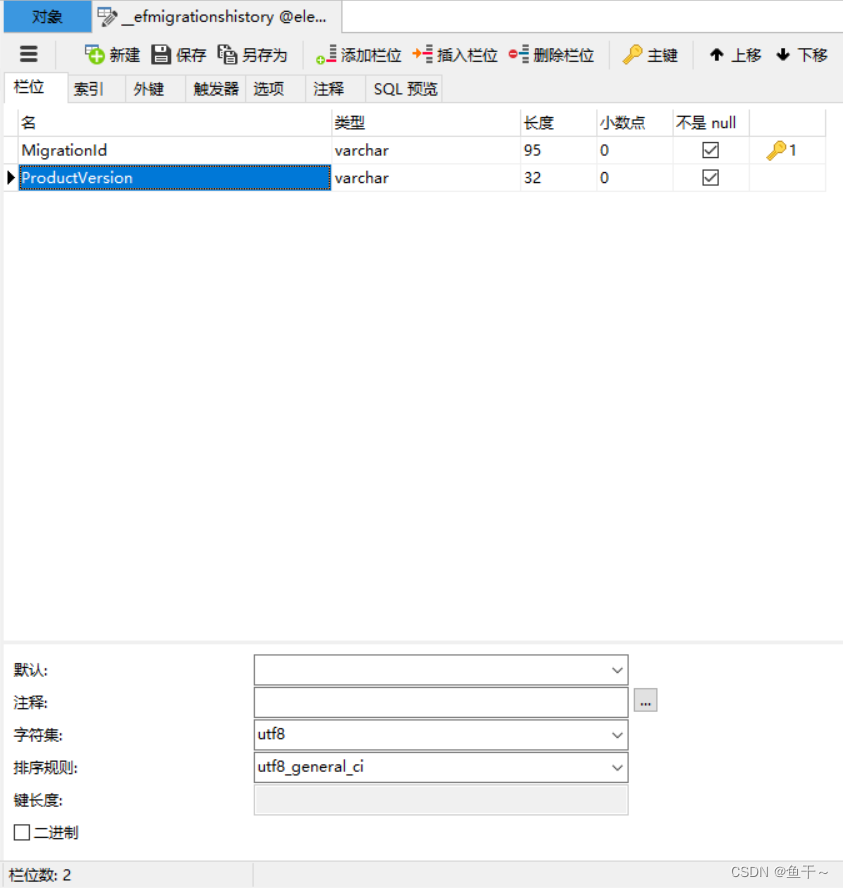
【mysql报错解决】MySql.Data.MySqlClient.MySqlException (0x80004005)或1366
场景:c#使用mysql数据库执行数据库迁移,使用了新增inserter的语句,然后报错 报错如下: 1.MySql.Data.MySqlClient.MySqlException (0x80004005): Incorrect string value: ‘\xE6\x9B\xB4\xE6\x94\xB9…’ for column ‘Migratio…...
Kafka-eagle监控平台
Kafka-Eagle简介 在开发工作中,当业务不复杂时,可以使用Kafka命令来进行一些集群的管理工作。但如果业务变得复杂,例如:需要增加group、topic分区,此时,再使用命令行就感觉很不方便,此时&#x…...

ubuntu16.04制作本地apt源离线安装
一、首先在有外网的服务器安装需要安装的软件,打包deb软件。 cd /var/cache/apt zip -r archives.zip archives sz archives.zip 二、在无外网服务器上传deb包,并配置apt源。 1、上传deb包安装lrzsz、unzip 用ftp软件连接无外网服务器协议选择sftp…...

【Leetcode】91.解码方法
一、题目 1、题目描述 一条包含字母 A-Z 的消息通过以下映射进行了 编码 : A -> "1" B -> "2" ... Z -> "26"要 解码 已编码的消息,所有数字必须基于上述映射的方法,反向映射回字母(可能有多种方法)。例如,"11106" …...

easyx图形库基础:2.基本运动+键盘交互
基本运动键盘交互 一.基本运动1.基本运动:1.如何实现动画:2.实现一个小球从左到右从右到左:(往返运动)3.实现一个五角星的移动:4.实现一个五角星自转和圆周运动的集合:(圆周运动&…...
计算机竞赛 opencv 图像识别 指纹识别 - python
0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 基于机器视觉的指纹识别系统 🥇学长这里给一个题目综合评分(每项满分5分) 难度系数:3分工作量:3分创新点:4分 该项目较为新颖,适…...

UI自动化测试常见的Exception
一. StaleElementReferenceException: - 原因:引用的元素已过期。原因是页面刷新了,此时当然找不到之前页面的元素。- 解决方案:不确定什么时候元素就会被刷新。页面刷新后重新获取元素的思路不变,这时可以使用python的…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

MySQL 主从同步异常处理
阅读原文:https://www.xiaozaoshu.top/articles/mysql-m-s-update-pk MySQL 做双主,遇到的这个错误: Could not execute Update_rows event on table ... Error_code: 1032是 MySQL 主从复制时的经典错误之一,通常表示ÿ…...
:LeetCode 142. 环形链表 II(Linked List Cycle II)详解)
Java详解LeetCode 热题 100(26):LeetCode 142. 环形链表 II(Linked List Cycle II)详解
文章目录 1. 题目描述1.1 链表节点定义 2. 理解题目2.1 问题可视化2.2 核心挑战 3. 解法一:HashSet 标记访问法3.1 算法思路3.2 Java代码实现3.3 详细执行过程演示3.4 执行结果示例3.5 复杂度分析3.6 优缺点分析 4. 解法二:Floyd 快慢指针法(…...

对象回调初步研究
_OBJECT_TYPE结构分析 在介绍什么是对象回调前,首先要熟悉下结构 以我们上篇线程回调介绍过的导出的PsProcessType 结构为例,用_OBJECT_TYPE这个结构来解析它,0x80处就是今天要介绍的回调链表,但是先不着急,先把目光…...

电脑桌面太单调,用Python写一个桌面小宠物应用。
下面是一个使用Python创建的简单桌面小宠物应用。这个小宠物会在桌面上游荡,可以响应鼠标点击,并且有简单的动画效果。 import tkinter as tk import random import time from PIL import Image, ImageTk import os import sysclass DesktopPet:def __i…...
