leetcode 力扣刷题 滑动窗口 部分题解(记录)
力扣刷题 滑动窗口相关的部分题解
- 209. 长度最小的子数组
- 904. 水果成篮
- 76. 最小覆盖子串
209. 长度最小的子数组
leetcode题目链接 209.长度最小的子数组
题目内容是这样的:给定一个含有 n个正整数的数组和一个正整数 target 。
找出该数组中满足其和 ≥ target 的长度最小的连续子数组 [numsl, numsl+1, …, numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0。
理解题意,是要找到这样的连续子数组,满足条件①子数组元素之和≥target;②目标子数组是所有满足条件①的数组中,所含元素个数最少的。 这里强调连续子数组,是因为可能存在题目要求——找到数组中的最少的几个元素,使得元素之和≥target。
寻找连续子数组,可以使用最简单的暴力求解,两遍循环找到答案,时间复杂度O(N^2)。
在暴力求解中,很多子集的寻找是没有必要的,比如下面的情况:子数组[3, 1, 2 ,4]的和已经满足≥target,题意中说明了是正整数数组,那么再往后增加元素,子数组之和会继续增大(一定满足题意),但是子数组的长度也会增大,然而我们的目标是找到满足和≥target的长度最短的子数组。因此在一个子数组之后满足≥target后,固定i,j继续增大是没有必要的。

这道题目可以使用滑动窗口解决,时间复杂度O(N)。思路:
- 1、首先两个指针left和right,分别表示子数组的边界;
- 2、固定left,right向右移动,寻找到和≥target的子数组后停止! ——此时的子数组之和是从nums[left]+……+nums[right],是从左往右累加达到了目标,没有nums[right]子数组的和是<target的,但是没有nums[left]呢?那就不一定啦~ ——因此,接下来就是在这个满足了≥target要求的可行解上,寻找最优解。
- 3、固定right,left向右移动。逐步缩小子数组的长度的同时,验证子数组和是否满足≥target。left一直向右移动,直到子数组和<target,那么此时的left向左一位就是在这个子数组中满足条件的最短的子子数组了。
- 4、此时的left和right之间的数组不满足≥target了,并且在right之前的子数组都探索了,因此重复2-3,遍历完整个数组。
代码如下(C++):
class Solution {
public:int minSubArrayLen(int target, vector<int>& nums) {int n = nums.size();int ans = INT_MAX;int start = 0, end = 0, sum = 0;while(end < n){sum+=nums[end];while(sum>=target){//满足循环要求(题目要求)进入循环,判断当前子数组长度和ans哪个更短,更新ans = end - start + 1 < ans ? end - start + 1 : ans;sum -= nums[start];//移除掉start,即left元素,尝试缩短子数组的长度,寻找最优解start++;}end++;//end,即right要一直向右移动到知道sum>=target才会进入下面的循环}//注意最后可能没有解,所以子数组长度是0return ans == INT_MAX ? 0 : ans;}
};
904. 水果成篮
leetcode题目链接 904. 水果成篮

理解题意:①只有两个篮子,那么就只能采摘两种水果;②选择一棵树开始,比如是fruits[left],那么从这颗树开始,每棵树摘一颗果子,直到遇到第三种果树停止,假设是fruits[right];③要寻找right - left + 1最大(摘得的果子数最多)的情况。
简化题意:只包含两种果树的最长连续子数组。
解题思路(滑动窗口):
- 1、用left、right表示子数组的下标,left=0,right=0;kindleft = fruits[left]表示第一种水果,kindright = fruits[right]表示第二种水果;先固定left不变,right向右移动;
- 2、如果fruits[right]是left~right-1子数组的两种元素之一,即两种水果kindleft、kindright之一,right就继续向右移动;过程中更新ans;
- 3.1、如果如果fruits[right]既不是kindleft也不是kindright,即出现了第三种水果,那么当前的子数组的两个元素应该更新。更新为哪两种呢?①可以肯定的是fruits[right]是一种新水果;②另外一种是fruits[right-1](可能是kindleft也可能是kindright)——因为fruits[right] ≠ kindleft && fruits[right] ≠ kindright,但是fruits[right] =kindleft || fruits[right] = kindright,可以得到fruits[right] ≠ fruits[right-1],而子数组是连续的且只能包含两种元素,因此就是fruits[right] 和 fruits[right-1]。
- 3.2 更新子数组中包含的两种新元素后,新的子数组长度也需要更新,即更新left。left从right-1向左移动,直到找到不等于fruits[right-1]的下标(因为子数组中只能包括两种元素)。
代码(C++):
class Solution {
public:int totalFruit(vector<int>& fruits) {//记录子数组下标int left = 0, right = 0;//记录两种水果——即子数组中的两种元素int kindleft = fruits[left], kindright = fruits[right];//答案——水果数量int ans = 0;while(right < fruits.size()){//right向右移动,如果是left~right-1子数组中的元素,并入子数组if(fruits[right] == kindright || fruits[right] == kindleft){ans = max(ans, right - left + 1 );right++;}else{//如果fruits[right]是第三种水果,更新kindleft、kindrightkindright = fruits[right];left = right - 1;kindleft = fruits[left];//更新left,找到并入了新水果品种后的子数组的左边界while(left>=1 && fruits[left-1] == kindleft) left--;ans = max(ans, right - left + 1);} }return ans;}
};
76. 最小覆盖子串
leetcode题目链接 76. 最小覆盖子串
题目内容如下: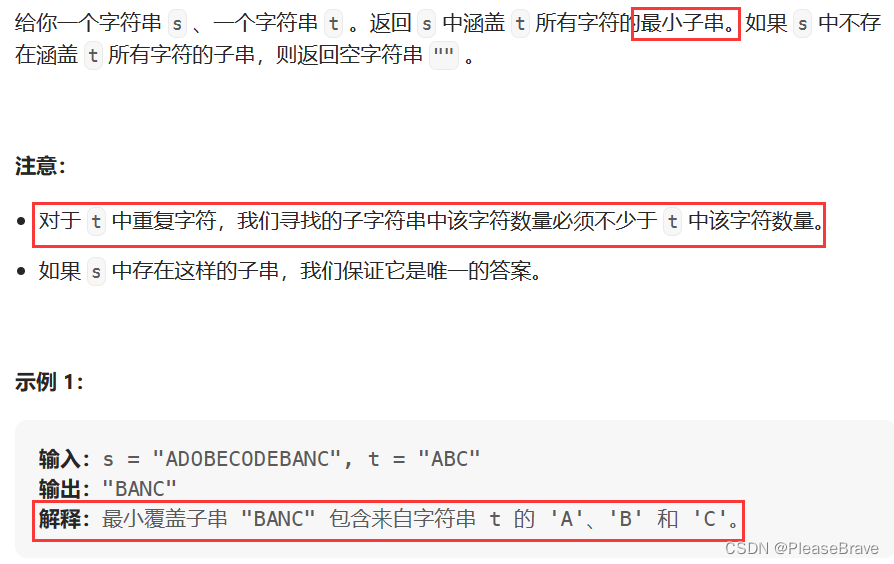
理解题意是寻找s中的最小子串,该子串能够包含t中的全部元素,根据示例可以看出,t中元素的顺序是不重要的;对于重复元素在子串中出现次数不少于在t中重复次数。
问题:在不要求字符顺序的前提下,如果确定子串substring中包含了t中全部元素?—— 对比 字符频数。即统计字符串t中字符及其频数,然后substring更新的过程中也记录子串中包含的t中元素的频数。 直到substring中包含了t中全部元素,并且对应频数≥t中对应元素的频数。 代码实现用distance表示两者差异,substring中新增一个t中的元素时,distance - 1,直到distance = 0,表示子串substring中包含了t中全部元素。
滑动窗口解题思路:
- 1、子串的左右下标用left、right表示。先寻找到一个包含了t中全部元素的子串,固定left,right向右移动。移动过程中如果s[right]是t中元素,那么就统计其频数,如果此时该元素频数已经>t中该元素频数,那么该元素的累积对减少两者的差异没有作用了,即distance不变化;如果该元素的频数 ≤ t中该元素的频数,distance - 1;如果s[right]不是t中元素,直接right++;
- 2、直到distance == 0时,找到了包含t中全部元素的子串,然后在子串中寻找最优解。固定right,left向右移动,left++。如果s[left]是t中元素,删除s[left]后,对应子串中关于s[left]的频数-1,如果减一后 ≥ t中该元素的频数,不会改变此时子串仍然是包含t中全部元素的事实,更新left,同时更新ans;如果如果减一后<t中该元素的频数,那么此时子串与t中元素的差异增加一个,distance++;
- 3、重复1-2,直到遍历完s。
代码如下(C++):
class Solution {
public:string minWindow(string s, string t) {int left = 0, right = 0;//记录子串的在S中的左右下标 unordered_map<int,int> T_freq, Sub_freq; //记录t中元素及其频数,记录子串中对应t中元素的频数 int distance = t.size(); //distance表示子串中包含的t中对应元素(及数量)与t的差异 int ans_left = 0, ans_right = s.size() -1; //记录最终目标子串的左右下标 int flage = 0; //记录s中是否存在包括t中全部元素的子串 for(int i = 0; i < t.size(); i++) T_freq[t[i]]++; //统计t中元素及其频数while(right < s.size()){ //遍历s 先固定left,right向右移动//如果s[right]是t中的元素,将其统计在子串的频数中if(T_freq.count(s[right]) != 0){Sub_freq[s[right]]++;//如果还没有包含完t中对应元素,那么新增一个s[right],子串和t的差异-1//如果已经包含了,那么s[right]只是在频数上有累计,但是子串和t的差异不变if(Sub_freq[s[right]] <= T_freq[s[right]])distance--;}//如果distance=0,即子串中已经包含了t中全部元素,固定right,left向右移动,缩短子串长度寻找最优解while(!distance){flage = 1;//一旦distance=0,即存在满足条件的子串,不会返回空串""//更新结果if(ans_right - ans_left > right - left) {ans_right = right;ans_left = left;}//如果删除的s[left]不是t中元素,直接删除,不会影响子串中包含了t中全部元素的事实//如果删除的s[left]是t中元素if(T_freq.count(s[left]) !=0 ){Sub_freq[s[left]]--;//需要更新子串中对应s[left]的频数//更新频数后可能还是包含t中全部元素的,比如t中a有2个,子串中a有4个,s[left]=a,之后子串中有3个a,但是还是包含了t中全部元素//如果不能全部包含了,子串和t的差异+1;if(Sub_freq[s[left]]<T_freq[s[left]])distance++;}left++; //删除s[left]后left右移;}right++;}if(flage) return s.substr(ans_left , ans_right - ans_left + 1);else return "";}
};
相关文章:

leetcode 力扣刷题 滑动窗口 部分题解(记录)
力扣刷题 滑动窗口相关的部分题解 209. 长度最小的子数组904. 水果成篮76. 最小覆盖子串 209. 长度最小的子数组 leetcode题目链接 209.长度最小的子数组 题目内容是这样的:给定一个含有 n个正整数的数组和一个正整数 target 。 找出该数组中满足其和 ≥ target 的…...

Intellij IDEA SBT依赖分析插件
可分析模块和传递依赖 安装完插件后,由于IDEA BUG,会出现两个分析按钮,一个是gradle的,一般是后者是新安装的sbt。 选择需要分析的模块 只需要在project/plugins.sbt中添加代码,启动官方分析插件addDependencyTreeP…...
MySQL中事务特性以及隔离机制
目录 一、什么是事务 二、事务特性——即ACID特性 三、事务的隔离级别 1、脏读 2、不可重复读 3、幻读 Read uncommitted: Read committed: Repeatable read: Serializable: 一、什么是事务 事务(Transaction)——一个最…...

Docker知识(详细笔记)
概览图 文章目录 概览图docker 知识速查1. 初识 Docker1.1 概念1.2 特点1.3 架构1.4 应用场景1.5 安装 Docker1.6 配置 Docker 镜像 2. Docker 命令2.1 Docker 进程相关命令2.2 Docker 镜像相关命令2.3 Docker 容器相关命令 3. Docker 容器的数据卷3.1 数据卷概念及作用3.1.1 概…...

【C#】获取已安装的NETFramework版本集合
代码 /// <summary>/// Windows信息/// </summary>public partial class WindowsInfo{/// <summary>/// 获取已安装的NETFramework版本集合/// </summary>/// <returns></returns>public static List<string> GetInstalledNETFramew…...

对字符串中所有单词进行倒排-C语言/Java
描述 输入一个字符串,输出字符串中单词的倒序。 要求 构成单词的字符只有26个大写或小写英文字母。非构成单词的字符均视为单词间隔符;倒排后的单词间隔符以一个空格表示;如果原字符串中相邻单词间有多个间隔符时,倒排转换后也只…...

Kubernetes入门 四、Pod核心
目录 什么是PodPod与容器不同Pod如何管理多个容器Pod的管理-工作负载K8s中的资源清单创建使用Pod直接创建Pod使用 Deployment 创建Pod 环境变量重启策略镜像拉取策略访问 DNS 的策略资源限制初始化容器临时容器(了解) 什么是Pod Pod 是可以在 Kubernete…...

【JAVA】数组练习
⭐ 作者:小胡_不糊涂 🌱 作者主页:小胡_不糊涂的个人主页 📀 收录专栏:浅谈Java 💖 持续更文,关注博主少走弯路,谢谢大家支持 💖 数组练习 1. 数组转字符串2. 数组拷贝3.…...
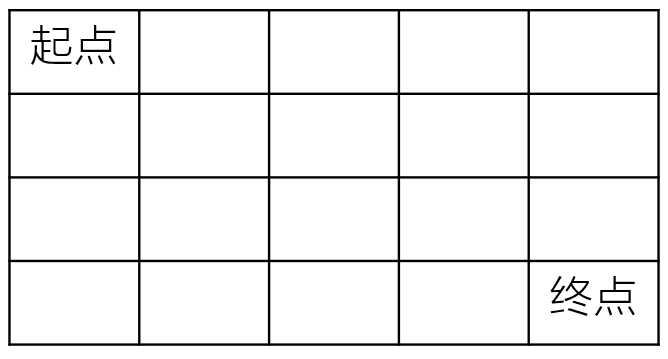
每日一题——不同路径的数目(一)
题目 一个机器人在mn大小的地图的左上角(起点)。 机器人每次可以向下或向右移动。机器人要到达地图的右下角(终点)。 可以有多少种不同的路径从起点走到终点? 数据范围:0<n,m≤100,保证计算结…...

innodb的锁
一致性锁定读和一致性非锁定读 Read Committed和Repetable Read级别下采用MVCC 实现非锁定读 但在一些情况下,要使用加锁来保障数据的逻辑一致性 自增列 锁的算法 唯一值 MySQL 中关于gap lock / next-key lock 的一个问题_呜呜呜啦啦啦的博客-CSDN博客 RR可以通过…...
Jmeter-压力测试工具
文章目录 Jmeter快速入门1.1.下载1.2.解压1.3.运行 2.快速入门2.1.设置中文语言2.2.基本用法 Jmeter快速入门 1s内发送大量请求,模拟高QPS,用以测试网站能承受的压力有多大 Jmeter依赖于JDK,所以必须确保当前计算机上已经安装了JDK࿰…...
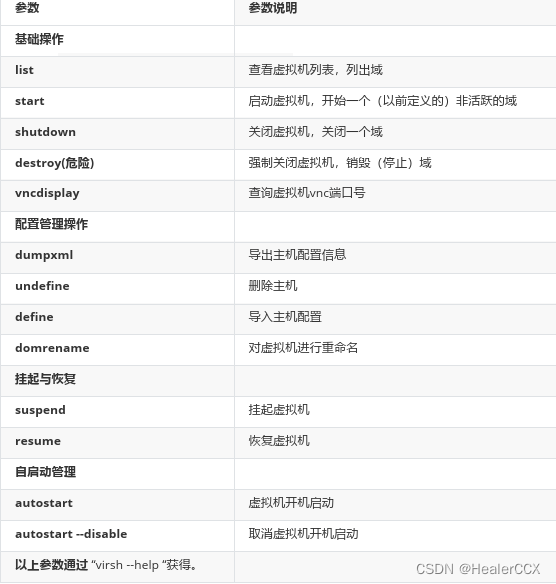
【KVM虚拟化环境部署】
环境部署 KVM虚拟化环境 1、装系统时手动选择安装 2、CentOS 7 最小化安装 yum install qemu-kvm qemu-img libvirt -y yum install virt-install libvirt-python virt-manager python-virtinst libvirt-client -y安装好CentOS 7后,去设置里面点击处理器&#x…...
030 - 定点类型(精确值)
-DECIMAL,NUMERIC: 该DECIMAL和NUMERIC 类型的存储精确的数值数据。当保留精确度很重要时,例如使用货币数据,则可以使用这些类型。在MySQL中,NUMERIC实现为DECIMAL,因此以下有关的说明DECIMAL同样适用于 NU…...

生活随笔,记录我的日常点点滴滴.
前言 😘个人主页:曲终酣兴晚^R的小书屋🥱 😕作者介绍:一个莽莽撞撞的🐻 💖专栏介绍:日常生活&往事回忆 😶🌫️每日金句:被人暖一下就高热&…...
C语言:每日一练(选择+编程)
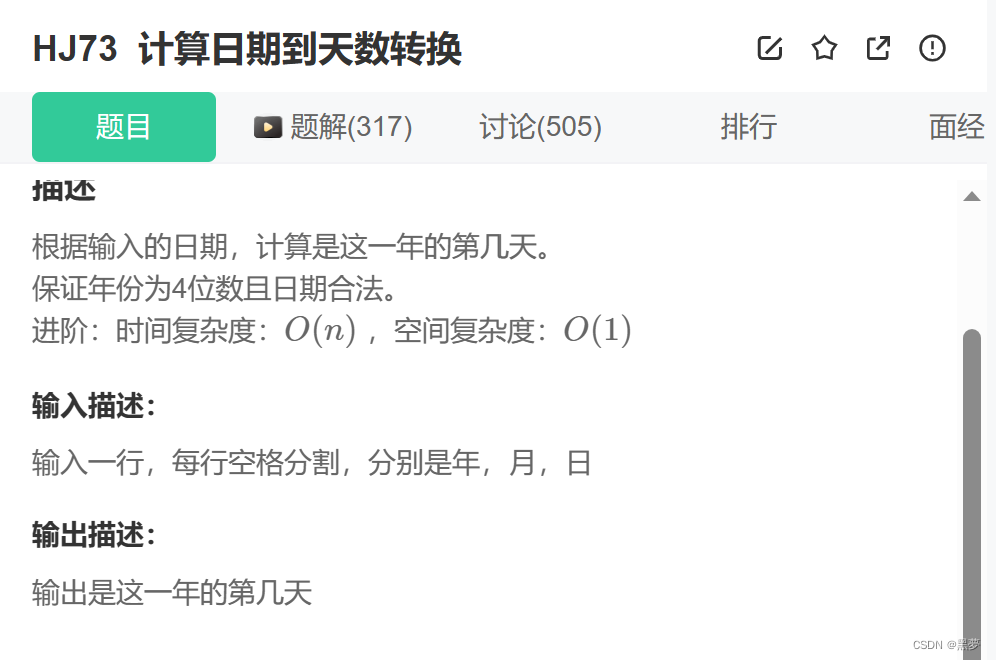
目录 选择题: 题一: 题二: 题三: 题四: 题五: 编程题: 题一:打印1到最大的n位数 示例1 思路一: 题二:计算日期到天数转换 示例1 思路一…...

Prompt、RAG、微调还是重新训练?选择正确的生成式 AI 的方法指南
文章目录 一、前言二、主要内容三、总结 🍉 CSDN 叶庭云:https://yetingyun.blog.csdn.net/ 一、前言 这篇博客试图根据一些常见的可量化指标,为您选择适合您用例的生成式人工智能方法提供指导。 生成式 AI 正在以惊人的速度发展,…...

Java实现单例模式的几种方法
单例模式作为23中设计模式中最基础的设计模式,一般实现方式为 ①私有化构造方法 ②提供一个获取对象的静态方法 除此之外,实现单例模式的方法还有很多种,这篇文章主要介绍实现单例模式的几种方法。 目录 一、懒汉式单例 二、懒汉式单例优化…...
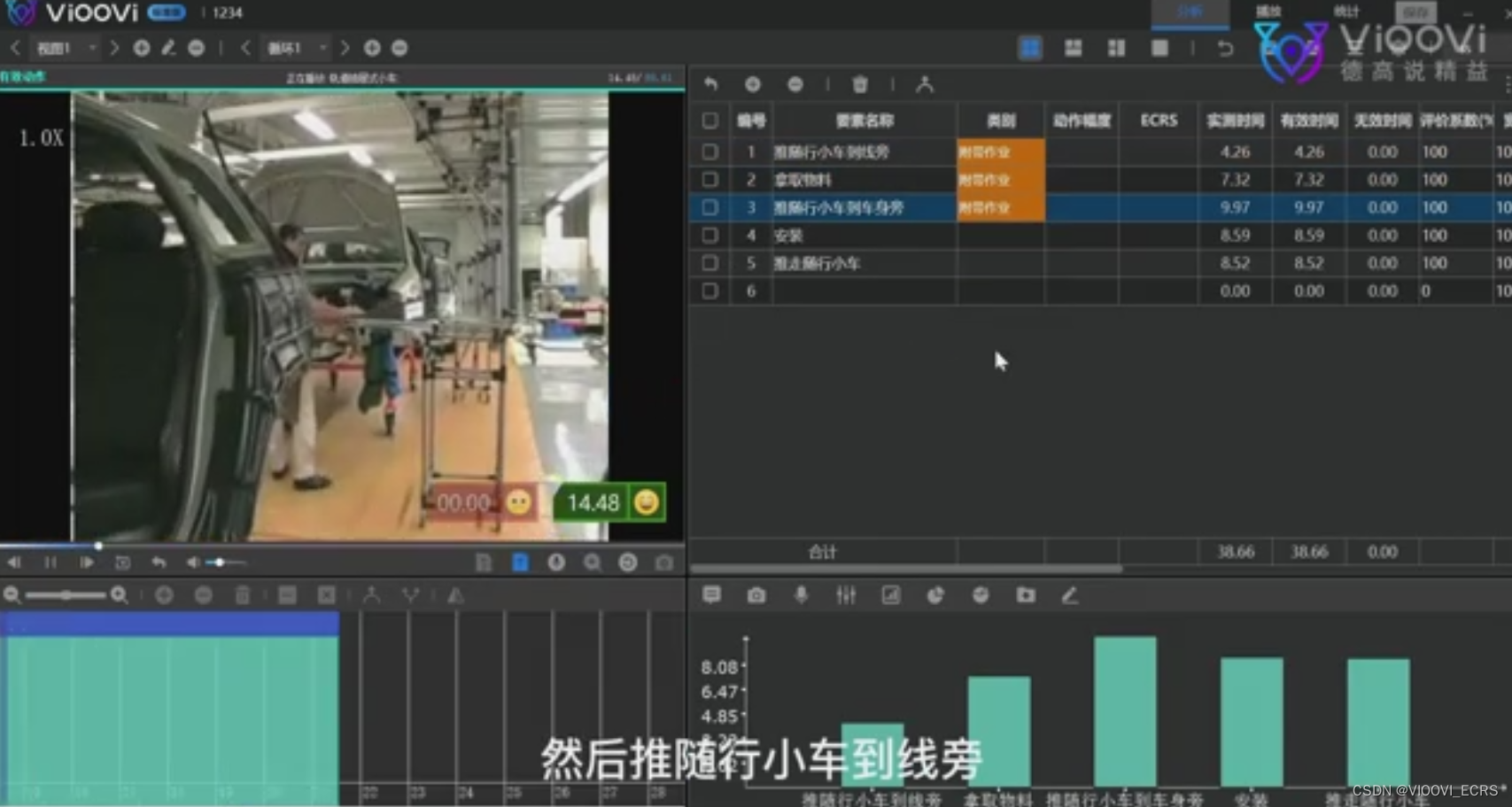
VIOOVI:标准的作业规范要求是什么?标准化作业规范怎么写?
本文围绕“标准化作业”展开论述,分享一些关于标准化作业以及标准的作业规范等相关知识。 什么是标准化作业? 标准化作业是一种以人的行为为中心,在一个操作序列中有效地进行生产而没有浪费的操作方法。 标准化作业的前提即:关注…...

WPF中的GridSplitter使用原则
WPF中的GridSplitter使用原则 GridSplitter对象必须放在Grid单元格中。可以预留一行或者列的Height或Width属性设置为auto。GridSplitter对象总是改变整行或整列的尺寸,为使该对象外观和行为保持一致,需要拉伸GridSplitter对象使其穿越整行或整列&#…...
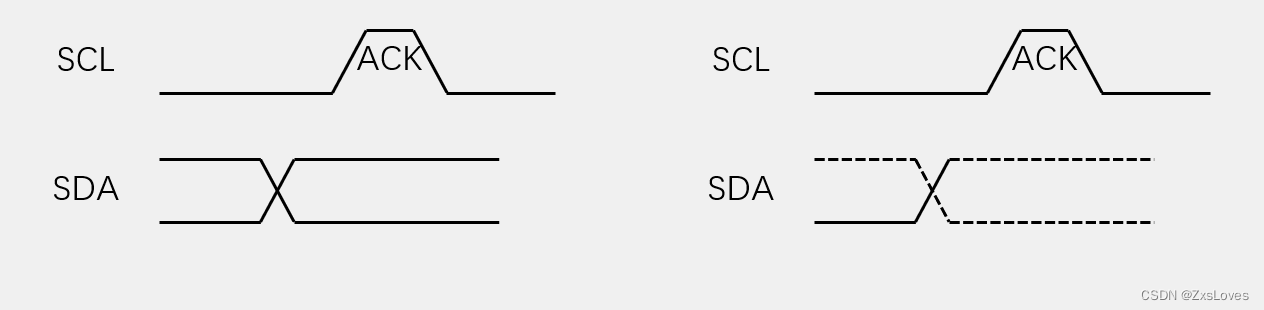
【【STM32----I2C通信协议】】
STM32----I2C通信协议 我们会发现I2C有两根通信线: SCL和SDA 同步 半双工 带数据应答 支持总线挂载多设备(一主多从,多主多从) 硬件电路 所有I2C设备的SCL连在一起,SDA连在一起 设备的SCL和SDA均要配置成开漏输出模式 …...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...
