第三章,矩阵,08-矩阵的秩及相关性质
第三章,矩阵,08-矩阵的秩及相关性质
- 秩的定义1
- 最高阶非零子式
- 定理
- 秩的定义2
- 秩的性质
- 性质1
- 性质2
- 性质3
- 性质4
- 性质5
- 性质6
- 性质7
- 性质8
- 性质9
- 性质10
- 性质11
- 性质12
- 性质12的推论
玩转线性代数(20)矩阵的秩的笔记,相关证明以及例子见原文
秩的定义1
设矩阵 A m ∗ n A_{m*n} Am∗n,称其标准形中单位矩阵子块的阶数为矩阵A的秩,记为 R ( A ) R(A) R(A)
最高阶非零子式
设在矩阵A中有一个r阶子式 D ≠ 0 D \neq 0 D=0,且所有r+1阶子式(如果存在的话)全等于0,那么D称为矩阵A的最高阶非零子式。
定理
设 A r ∼ B A^r \sim B Ar∼B,则A与B中最高阶非零子式的阶数相等
秩的定义2
由定理得定义2:一个矩阵的秩为它的最高阶非零子式的阶数
秩的性质
首先要了解判断矩阵的秩的依据有三点:
1、矩阵的秩为最高阶非零子式的阶数;
2、矩阵的秩为行阶梯的非零行数或列阶梯的非零列数或标准形中单位矩阵的阶数;
3、初等变换不改变矩阵的秩.
性质1
零矩阵的秩是零
性质2
若 A ≠ 0 A\neq0 A=0则 R ( A ) ≥ 1 R(A)\geq1 R(A)≥1
性质3
若A为m*n矩阵,则 0 ≥ R ( A ) ≥ m i n { m , n } 0\geq R(A)\geq min\{m,n\} 0≥R(A)≥min{m,n}
性质4
若 A = ( B ∗ ∗ ∗ ) A= \begin{pmatrix} B & * \\* & * \end{pmatrix} A=(B∗∗∗)是一个分块矩阵,B是A的子块,则 R ( A ) ≥ R ( B ) R(A)\geq R(B) R(A)≥R(B)
性质5
若 A m ∗ n A_{m*n} Am∗n中有一个s阶非零子式,则 R ( A ) ≥ s R(A)\geq s R(A)≥s;若 A m ∗ n A_{m*n} Am∗n中所有t阶子式都为0,则 R ( A ) < t R(A)\lt t R(A)<t
性质6
对任意矩阵A,有 R ( A T ) = R ( A ) R(A^T)=R(A) R(AT)=R(A)
性质7
( A 0 0 B ) \begin{pmatrix} A & 0 \\0 & B \end{pmatrix} (A00B)是一个分块矩阵,A、B是其子块,则 R ( A 0 0 B ) = R ( A ) + R ( B ) R\begin{pmatrix} A & 0 \\0 & B \end{pmatrix}= R(A) + R(B) R(A00B)=R(A)+R(B)
性质8
( A 0 B 0 ) \begin{pmatrix} A & 0 \\ B & 0 \end{pmatrix} (AB00)是一个分块矩阵,A、B是其子块,则 R ( A 0 B 0 ) ≤ R ( A ) + R ( B ) R\begin{pmatrix} A & 0 \\ B & 0 \end{pmatrix}\leq R(A) + R(B) R(AB00)≤R(A)+R(B)
性质9
对任意m*n矩阵A,B,无论对其进行加、减、横排、竖排,其秩均不超过 R ( A ) + R ( B ) R(A) + R(B) R(A)+R(B)
性质10
分块矩阵 ( A , B ) (A,B) (A,B)、 ( A B ) \begin{pmatrix} A \\ B \end{pmatrix} (AB)、 ( A 0 B 0 ) \begin{pmatrix} A & 0 \\ B & 0 \end{pmatrix} (AB00)的秩都满足 ≥ m a x ( R ( A ) , R ( B ) ) \geq max(R(A), R(B)) ≥max(R(A),R(B))
性质11
若 A ∼ B A \sim B A∼B则 R ( A ) = R ( B ) R(A)=R(B) R(A)=R(B)
性质12
若 A m n B n l = C A_{mn}B_{nl}=C AmnBnl=C且 R ( A ) = n R(A)=n R(A)=n,则 R ( B ) = R ( C ) R(B)=R(C) R(B)=R(C),可得若B行满秩,则 R ( A ) = R ( C ) R(A)=R(C) R(A)=R(C)
证:
只证明列满秩的情况,因 R ( A ) = n R(A)=n R(A)=n,知A行最简形矩阵为 ( E n O ) m ∗ n \begin{pmatrix} E_n \\ O \end{pmatrix}_{m*n} (EnO)m∗n,并且有m阶可逆矩阵P,使 P A = ( E n O ) PA=\begin{pmatrix} E_n \\ O \end{pmatrix} PA=(EnO),于是
P C = P A B = ( E n O ) B = ( B O ) PC=PAB=\begin{pmatrix} E_n \\ O \end{pmatrix}B=\begin{pmatrix} B \\ O \end{pmatrix} PC=PAB=(EnO)B=(BO)
知 R ( C ) = R ( P C ) R(C)=R(PC) R(C)=R(PC),而 R ( B O ) = R ( B ) R\begin{pmatrix} B \\ O \end{pmatrix}=R(B) R(BO)=R(B),故
R ( C ) = R ( B ) R(C)=R(B) R(C)=R(B)
本例中的A为列满秩矩阵,当A为方阵时,列满秩矩阵就成为满秩矩阵,也就是可逆矩阵。因此,本例的结论当A为方阵时B和C就是等价关系,当然秩相等。
性质12的推论
若 A m n B n l = O A_{mn}B_{nl}=O AmnBnl=O,且 R ( A ) = n R(A)=n R(A)=n,则B=O(矩阵乘法的消去律)
相关文章:

第三章,矩阵,08-矩阵的秩及相关性质
第三章,矩阵,08-矩阵的秩及相关性质 秩的定义1最高阶非零子式定理秩的定义2秩的性质性质1性质2性质3性质4性质5性质6性质7性质8性质9性质10性质11性质12性质12的推论 玩转线性代数(20)矩阵的秩的笔记,相关证明以及例子见原文 秩的定义1 设矩…...
VS2019 + Qt : setToolTip的提示内容出现乱码
VS2019 Qt : setToolTip的提示内容出现乱码 在使用setToolTip()时, setToolTip(QString("asd你好!");标签提示只有英文是对的,中文是乱码! 应该是编码出了问题。默认情况下,Qt使用的是UTF-8编码…...

PO、BO、VO、DTO、DAO、POJO
文章目录 PO(Persistant Object)持久对象DO(Data Object)数据对象AO(Application Object)应用对象BO(Business Object)业务对象VO(Value Object)表现对象DTO&…...
MySQL— 基础语法大全及操作演示!!!(下)
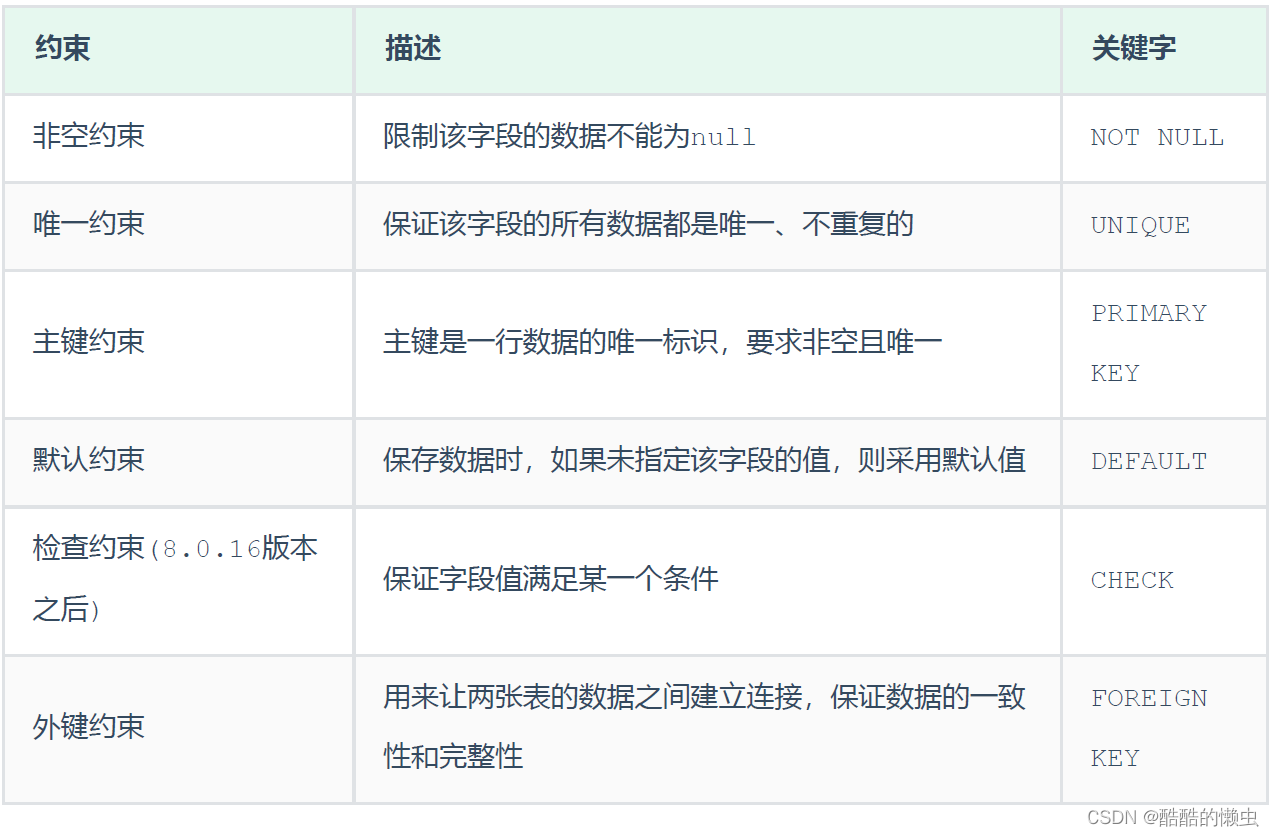
MySQL—— 基础语法大全及操作演示(下)—— 持续更新 三、函数3.1 字符串函数3.2 数值函数3.3 日期函数3.4 流程函数 四、约束4.1 概述4.2 约束演示4.3 外键约束4.3.1 介绍4.3.2 语法4.3.3 删除/更新行为 五、多表查询5.1 多表关系5.1.1 一对多5.1.2 多对…...

Springboot+vue网上招聘系统
系统的首页,头部有三个选项框,第一个是主页,第二个是才艺技能平台,第三个是登录注册。1.1.2 登录注册模块 系统的登录注册包括登录和注册两个部分。所有系统用户使用后台管理功能都需要经行登录,根据选择不同的身份进入…...

奥威BI数据可视化工具:报表就是平台,随时自助分析
别的数据可视化工具,报表就只是报表,而奥威BI数据可视化工具,一张报表就约等于一个平台,可随时展开多维动态自助分析,按需分析,立得数据信息。 奥威BI是一款多维立体分析数据的数据可视化工具。它可以帮助…...

iPhone(iPad)安装deb文件
最简单的方法就是把deb相关的文件拖入手机对应的目录,一般是DynamicLibraries文件夹 参考:探讨手机越狱和安装deb文件的几种方式研究 1、在 Mac 上安装 dpkg 命令 打包 deb 教程之在 Mac 上安装 dpkg 命令_xcode打包root权限deb_qq_34810996的博客-CS…...
手撕单链表
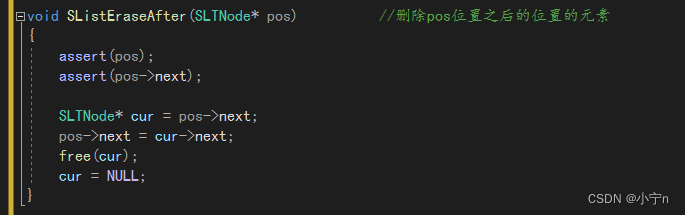
目录 链表的概念和结构 单链表的实现 申请新结点 打印 尾插 头插 尾删 头删 编辑 查找 在pos位置前插入元素 在pos位置后插入元素 删除pos位置的元素 删除pos位置之后的位置的元素编辑 完整代码 SListNode.h SListNode.c 链表的概念和结构 链表是一种物理存储…...
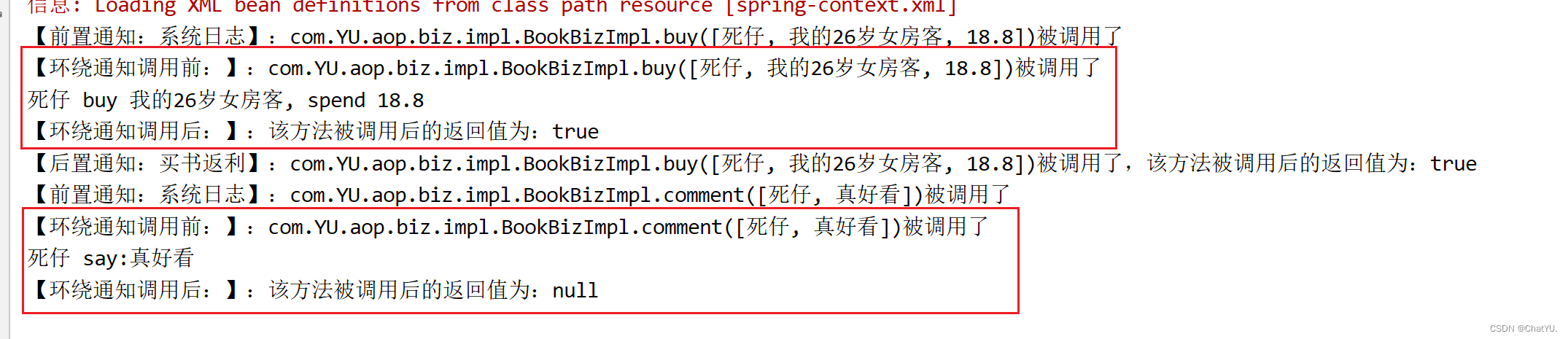
Spring-aop特点,专业术语及案例演示
一.aop简介 AOP(Aspect-Oriented Programming)是Spring框架的一个重要特性,它通过将横切关注点(cross-cutting concerns)从核心业务逻辑中分离出来,以模块化的方式在整个应用程序中重复使用。以下是关于AOP…...

探秘Java的Map集合:键值映射的奇妙世界
文章目录 1. 单列集合 vs. 双列集合2. Map接口:键与值的契约3. 深入探索HashMap3.1 特性与构造方法3.2 常用方法3.3 遍历HashMap 4. 美妙的LinkedHashMap 在Java编程中,集合是不可或缺的重要部分,它为我们提供了各种数据结构和算法的实现。其…...

git权限问题解决方法Access denied fatal: Authentication failed
文章目录 遇到Access denied 的权限问题解决方法1、git的密码修改过,但是本地没更新。2、确定问题,然后增加配置① 查询用户信息②如果名称和email不对,设置名称:③ 检查ssh-add是否链接正常④ 设置不要每次都输入用户名密码 3、配…...
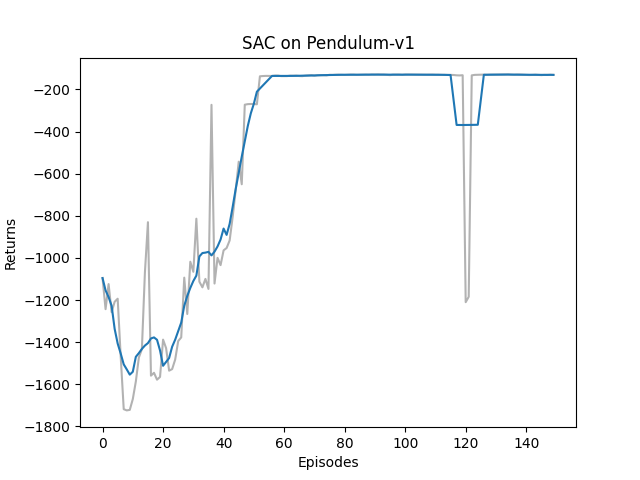
Hands on RL 之 Off-policy Maximum Entropy Actor-Critic (SAC)
Hands on RL 之 Off-policy Maximum Entropy Actor-Critic (SAC) 文章目录 Hands on RL 之 Off-policy Maximum Entropy Actor-Critic (SAC)1. 理论基础1.1 Maximum Entropy Reinforcement Learning, MERL1.2 Soft Policy Evaluation and Soft Policy Improvement in SAC1.3 Tw…...

JavaScript中的this指向,call、apply、bind的简单实现
JavaScript中的this this是JavaScript中一个特殊关键字,用于指代当前执行上下文中的对象。它的难以理解之处就是值不是固定的,是再函数被调用时根据调用场景动态确定的,主要根据函数的调用方式来决定this指向的对象。this 的值在函数被调用时…...
Linux学习之基本指令一
在学习Linux下的基本指令之前首先大家要知道Linux下一切皆目录,我们的操作基本上也都是对目录的操作,这里我们可以联想我们是如何在windows上是如何操作的,只是形式上不同,类比学习更容易理解。 目录 01.ls指令 02. pwd命令 0…...

appium默认60秒关闭应用的问题
问题:appium默认启动一个应用的session过期时间是60秒到时间会自动停了刚启动的应用,工作台打印:info: [debug] We shut down because no new commands came in的日志 分析:--command-timeout 60 The default command timeout fo…...
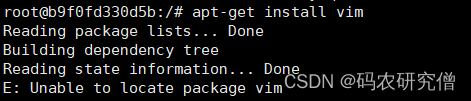
Docker 容器内无法使用vim命令 解决方法
目录 1. 问题所示2. 原理分析3. 解决方法1. 问题所示 进入Docker容器后 无法使用vim编辑器,出现如下问题:bash: vim: command not found 如图所示: 想着通过apt-get 安装vim,出现如下问题: root@b9f0fd330d5b:/# apt-get install vim Reading package lists... Done B…...
Django的简介安装与配置及两大设计模式
一.Djang的介绍 1.Django是什么 Django 是使用 Python 语言开发的一款免费而且开源的 Web 应用框架。 由于 Python 语言的跨平台性,所以 Django 同样支持 Windows、Linux 和 Mac 系统。 在 Python 语言炽手可热的当下,Django 也迅速的崛起,在…...

Mybatis分页插件——PageHelper
一、定义 PageHelper用在mybatis插件里面,可以自动的为最近的sql语句进行分页查询,提供分页的页码size和每页数量num,在查询过程中hi自动的拼接limit关键字,不用再改写sql语句了 在PageHelper.startPage(); 在启动查询…...

k8s认证详解 k8s证书详解 2023推荐
推荐阅读 https://www.yii666.com/blog/478731.html?actiononAll 在 Kube-apiserver 中提供了很多认证方式,其中最常用的就是 TLS 认证,当然也有 BootstrapToken,BasicAuth 认证等,只要有一个认证通过,那么 Kube-api…...

php初解
php是什么? PHP,全称 Hypertext Preprocessor ,中文翻译“超文本预处理器”。 PHP是一种被广泛应用的开源通用脚本语言,尤其适用于 Web 开发。 拥有快速,灵活,实用的特点,PHP能做任何事…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

在树莓派上添加音频输入设备的几种方法
在树莓派上添加音频输入设备可以通过以下步骤完成,具体方法取决于设备类型(如USB麦克风、3.5mm接口麦克风或HDMI音频输入)。以下是详细指南: 1. 连接音频输入设备 USB麦克风/声卡:直接插入树莓派的USB接口。3.5mm麦克…...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...

spring Security对RBAC及其ABAC的支持使用
RBAC (基于角色的访问控制) RBAC (Role-Based Access Control) 是 Spring Security 中最常用的权限模型,它将权限分配给角色,再将角色分配给用户。 RBAC 核心实现 1. 数据库设计 users roles permissions ------- ------…...

【深度学习新浪潮】什么是credit assignment problem?
Credit Assignment Problem(信用分配问题) 是机器学习,尤其是强化学习(RL)中的核心挑战之一,指的是如何将最终的奖励或惩罚准确地分配给导致该结果的各个中间动作或决策。在序列决策任务中,智能体执行一系列动作后获得一个最终奖励,但每个动作对最终结果的贡献程度往往…...

算法—栈系列
一:删除字符串中的所有相邻重复项 class Solution { public:string removeDuplicates(string s) {stack<char> st;for(int i 0; i < s.size(); i){char target s[i];if(!st.empty() && target st.top())st.pop();elsest.push(s[i]);}string ret…...
