当前位置：首页 > news >正文

数据结构----哈夫曼树

news 2026/2/10 14:16:56

这里写目录标题

基本概念
- 引子
- 基本概念
- - 各种路径长度
  - 各种带权路径长度
  - - 结点的带权路径长度
    - 树的带权路径长度
    - 哈夫曼树
- 哈夫曼树的构造
- - 理论基础
  - 构造思想
  - 总结
- 哈夫曼树的实现
- 哈夫曼编码
- - 前缀编码
  - 哈夫曼编码的思想
  - 案例
  - 代码实现
- 编码与解码

基本概念

引子

在这里插入图片描述

哈夫曼树就是寻找构造最优二叉树，用于提高效率

基本概念

各种路径长度

在这里插入图片描述

各种带权路径长度

结点的带权路径长度

在这里插入图片描述

树的带权路径长度

在这里插入图片描述

在这里插入图片描述

哈夫曼树

在这里插入图片描述
带权路径长度最短的树或者二叉树

也就是树的叶子结点带权路径长度之和：也就是叶子结点的结点路径长度（根结点到叶子结点的路径数） *权重再求和
在这里插入图片描述

总结：位高权重
并且哈夫曼树不唯一

哈夫曼树的构造

理论基础

在这里插入图片描述

构造思想

在这里插入图片描述
可以看到先将所有结点看成根结点构造出森林并将权重赋值给结点
之后选择两个小权重的结点二者构造出新树如上图新树根结点权重为子树结点权重之和
这时要先将森林中的两个树删除之后将两个树构造成的新树加入森林（为了进行下一次权重的比较从而下一步构造的顺利进行）
重复23步直到剩单根

在这里插入图片描述

度是指结点有的子树个数

哈夫曼树结点的度只能是0或者2
n个叶子结点的哈夫曼树一共有2n-1个结点分析如上橙色框

总结

在这里插入图片描述

哈夫曼树的实现

在这里插入图片描述
首先是已知叶子结点的个数以及权重

依次放入结构数组的前面数组一共长度是2n 因为结点一共有2n-1 所以构造2n的数组不用0下标

进行第二步合并的时候将新合并出来的结点往后依次放入所以根结点是数组中的最后一个位置

新节点合成的时候要修改新节点数组中的孩子结点下标两个孩子要修改数组中双亲的下标

之后重复查找最小的权重的两个结点前提是parent值是空这是判断的关键一旦parent值不为空的时候就相当于退出了比较

在这里插入图片描述

初始化

在这里插入图片描述
上图中select方法功能是在HT[K]中选择两个双亲域为0并且权重最小的结点并返回s1 s2 用于后续操作

方法参数中i-1 是新合成结点的下标，在选最小的两个结点时要从新节点前面选这里对应理论分析中“第三步的a步骤”
i会逐渐递增

哈夫曼编码

前缀编码

在这里插入图片描述
图中为非前缀编码所以要设计任意一个字符的编码都不是另一个字符编码的前缀
但是可以前缀一样后面不一样

哈夫曼编码的思想

在这里插入图片描述
要想出现次数最多的编码最短正好对应哈夫曼树的权重越大离跟结点越近的特点

所以在路径上标注0 或者 1
看从根结点到某一个叶子结点经过的路径那些路径得出来的编码就是字符对应的二进制编码

因为叶子结点不会出现一个字符的路径完全包含另一个字符的路径所以也就是前缀编码
并且要想出现次数最多的编码最短正好对应哈夫曼树的权重越大离跟结点越近的特点所以哈夫曼编码效率更高
在这里插入图片描述
因为叶子结点不会出现一个字符的路径完全包含另一个字符的路径所以也就是前缀编码
并且要想出现次数最多的编码最短正好对应哈夫曼树的权重越大离跟结点越近的特点所以哈夫曼编码效率更高

案例

在这里插入图片描述
先根据哈夫曼树的设计思想画出来哈夫曼树在路径上标注0 1

代码实现

在这里插入图片描述

其中HC数组是指针数组每个指针指向对应的字符串也就是字符串的头指针

编码与解码

在这里插入图片描述
进行哈夫曼编码时构造指针数组

先根据哈夫曼树的构造思想+字符频度表构造出哈夫曼树标上各个叶子结点代表的字符之后开始解码 0就向左走 1就向右走直到走到叶子结点记录一个字符重复此操作即可

相关文章：

数据结构----哈夫曼树

这里写目录标题基本概念引子基本概念各种路径长度各种带权路径长度结点的带权路径长度树的带权路径长度哈夫曼树哈夫曼树的构造理论基础构造思想总结哈夫曼树的实现哈夫曼编码前缀编码哈夫曼编码的思想案例代码实现编码与解码基本概念引子哈夫曼树就是寻找构造最优二叉…...

编程日记 2023/8/18 2:31:26

Spring之Aop切面---日志收集（环绕处理、前置处理方式）--使用/教程/实例

Spring之Aop切面---日志收集（环绕处理、前置处理方式）--使用/教程/实例简介系统登录日志类LoginLogEntity .java 一、环绕处理方式1、自定义注解类LoginLogAop.class2、切面处理类LogoutLogAspect.java 二、前置处理方式：1、自定义注解类Log…...

编程日记 2023/8/18 2:30:25

UE4/UE5 照明构建失败 “Lightmass crashed”解决“数组索引越界”

在构建全局光照时,经常会出现“Lightmass crashed”的错误,导致光照构建失败。本文将分析这一问题的原因,并给出解决建议。 UE4 版本4.26 报错如下： <None> Lightmass crashed: Assertion failed: (Index > 0) & (Index < ArrayNum) [File:d:\bu…...

编程日记 2023/8/18 2:29:21

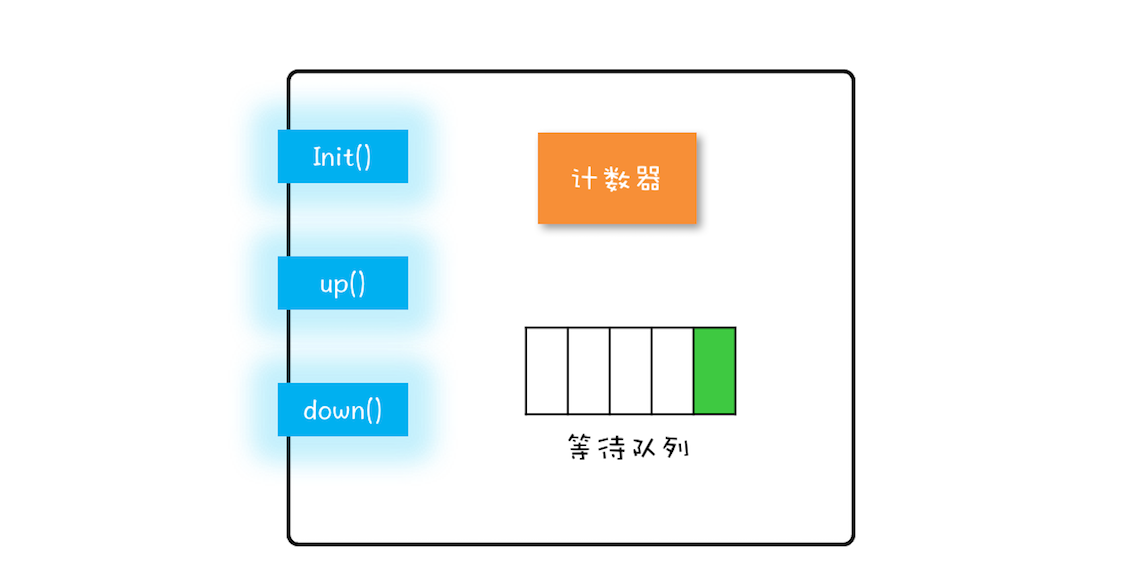
并发编程系列-Semaphore

Semaphore，如今通常被翻译为"信号量"，过去也曾被翻译为"信号灯"，因为类似于现实生活中的红绿灯，车辆是否能通行取决于是否是绿灯。同样，在编程世界中，线程是否能执行取决于信号量是否允…...

编程日记 2023/8/18 2:28:20

3年 Android 开发的面试心经（后悔当初没有拿 N+1）

作者：勇闯天涯当某人顺利通过大厂面试时，总会有人认为这是运气比较好罢了，但他们不曾得知对方之前受过多少苦和委屈，又付出了多少努力一步步去突破这些困境。正是因为他们的努力付出，在合适的时间与地点，用…...

编程日记 2023/8/18 2:27:18

【c语言】 -- 指针进阶

📕博主介绍：目前大一正在学习c语言，数据结构，计算机网络。 c语言学习，是为了更好的学习其他的编程语言，C语言是母体语言，是人机交互接近底层的桥梁。本章来学习指针进阶。让我们开启c语言学习…...

编程日记 2023/8/18 2:26:17

软件压力测试对软件产品起到什么作用?

一、软件压力测试是什么? 软件压力测试是一种通过模拟正常使用环境中可能出现的大量用户和大数据量的情况，来评估软件系统在压力下的稳定性和性能表现的测试方法。在软件开发过程中，经常会遇到一些性能瓶颈和稳定性问题，而软件压力测试的作…...

编程日记 2023/8/18 2:25:16

Stephen Wolfram：那么…ChatGPT 在做什么，为什么它有效呢？

So … What Is ChatGPT Doing, and Why Does It Work? 那么…ChatGPT在做什么，为什么它有效呢？ The basic concept of ChatGPT is at some level rather simple. Start from a huge sample of human-created text from the web, books, etc. Then train…...

编程日记 2023/8/18 2:24:14

机器学习基础（五）

决策树决策树是一种预测模型，它代表着对象属属性与对象值之间的一种映射关系。树中的每个节点代表一个对象，分叉路径（或者叫树枝）则代表一个属性值。决策树常用方法：分类树分析，是一种监督学习，用于预计结果可能为离散类型。回归树分析，用于预计结果为实数。 CART，…...

编程日记 2023/8/18 2:23:13

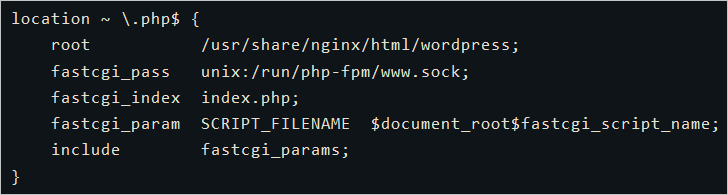
阿里云服务器安装WordPress网站教程基于CentOS系统

阿里云百科分享使用阿里云服务器安装WordPress博客网站教程，WordPress是使用PHP语言开发的博客平台，在支持PHP和MySQL数据库的服务器上，您可以用WordPress架设自己的网站，也可以用作内容管理系统（CMS）。本教…...

编程日记 2023/8/18 2:22:12

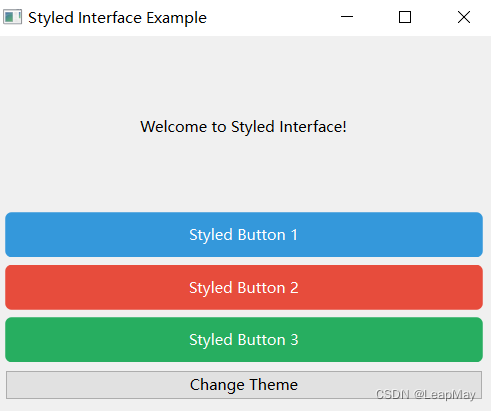
【100天精通python】Day37：GUI界面编程_PyQT从入门到实战（上）

目录专栏导读 1 PyQt6 简介： 1.1 安装 PyQt6 和相关工具： 1.2 PyQt6 基础知识： 1.2.1 Qt 的基本概念和组件： 1.2.2 创建和使用 Qt 窗口、标签、按钮等基本组件 1.2.3 布局管理器：垂直布局、水平布局、网格布局…...

编程日记 2023/8/18 2:21:11

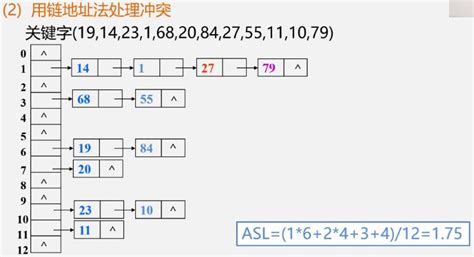
数据结构—散列表的查找

7.4散列表的查找 7.4.1散列表的基本概念基本思想：记录的存储位置域关键字之间存在对应关系对应关系——hash函数 Loc（i） H（keyi） 如何查找： 根据散列函数 H(key) k 查找key9，则访…...

编程日记 2023/8/18 2:20:09

Expo项目使用Native base UI库

装包： yarn add native-base expo install react-native-svg12.1.1 Index.js: import React from react import { View, Text } from react-native import useList from ./useList import { NativeBaseProvider, Button, Box } from native-base import styles f…...

编程日记 2023/8/18 2:19:08

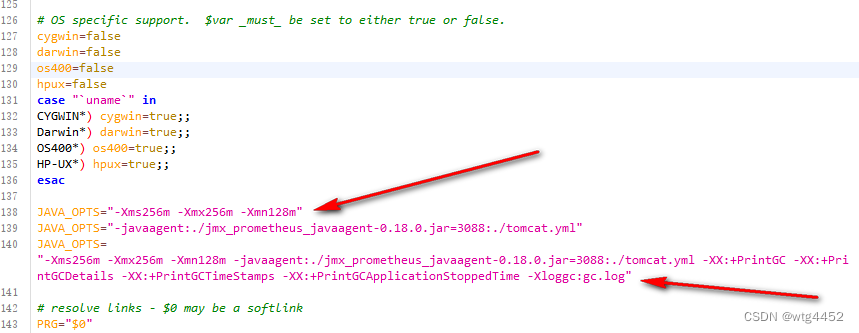
74、75、76——tomcat项目实战

tomcat项目实战 tomcat 依赖 java运行环境，必须要有jre ，选择 jdk1.8 JvmPertest 千万不能用 kyj易捷支付项目机器选择一台机器，安装jdk1.8的机器下载tomcat的包上传到机器，解压tomcattomcat文件 bin文件夹：启动文件堆栈配置文件 catalina.sh JAVA_OPTS="-Xm…...

编程日记 2023/8/18 2:18:06

jmeter errstr :“unsupported field type for multipart.FileHeader“

在使用jmeter测试接口的时候，提示errstr :"unsupported field type for multipart.FileHeader"如图所示这是因为我们在HTTP信息头管理加content-type参数有问题直接在HTTP请求中，勾选： use multipart/form-data for POST【中文…...

编程日记 2023/8/18 2:17:05

C#调用C++ DLL传参byte[]数组字节值大于127时会变为0x3f的问题解决

最近做了一个网络编程的DLL给C#调用，DLL中封装了一个TCP Client的函数接口，如下所示 //C TCP报文发送接口 int TcpClient_send(unsigned char* buffSend, unsigned int nLen) {unsigned char buff[1024];int len StringToHex(buffSend, buff);int nRet…...

编程日记 2023/8/18 2:16:03

【vue3+xlxs+xlsx-style-vite】vue3项目中使用xlsx插件实现Excel表格的导出和解析，已实现

在vue3项目中使用xlsx插件实现Excel表格的导出和解析 1、xlsx插件包官方 xlsx插件包官方 2、FileReader官方文档：FileReader官方文档安装xlsx和xlsx-style-vite、file-saver npm install xlsx npm install xlsx-style-vite npm install file-saverpackage.json中查…...

编程日记 2023/8/18 2:15:02

Doris2.0时代的一些机遇和挑战！

300万字！全网最全大数据学习面试社区等你来！ 上个周五的时候，Doris官宣了2.0版本，除了在性能上的大幅提升，还有一些特性需要大家特别关注。根据官网的描述，Doris在下面领域都有了长足进步： 日志…...

编程日记 2023/8/18 2:14:00

Leetcode-每日一题【剑指 Offer 32 - I. 从上到下打印二叉树】

题目从上到下打印出二叉树的每个节点，同一层的节点按照从左到右的顺序打印。例如: 给定二叉树: [3,9,20,null,null,15,7], 3 / \ 9 20 / \ 15 7 返回： [3,9,20,15,7] 提示： 节点总数 < 1000 解题思路 1.题目要求我们从…...

编程日记 2023/8/18 2:12:59

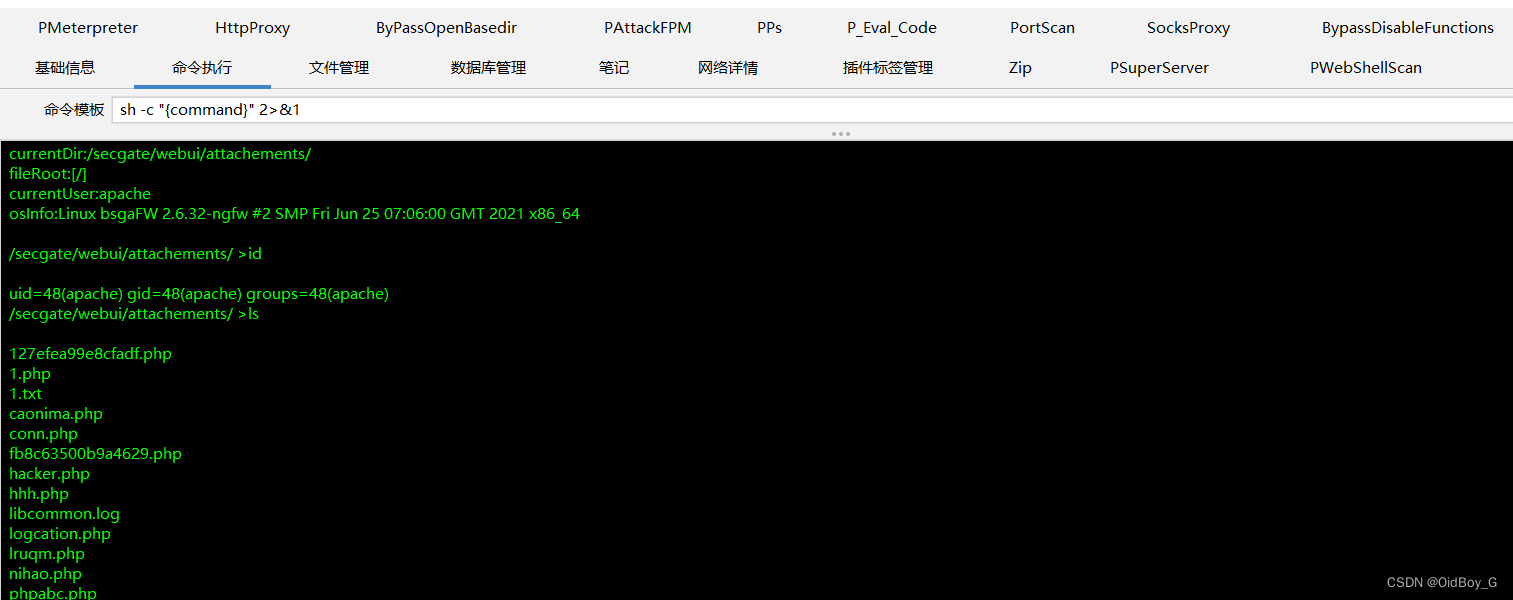
网神 SecGate 3600 防火墙任意文件上传漏洞复现

0x01 产品简介网神SecGate3600下一代极速防火墙（NSG系列）是基于完全自主研发、经受市场检验的成熟稳定网神第三代SecOS操作系统并且在专业防火墙、VPN、IPS的多年产品经验积累基础上精心研发的高性能下一代防火墙专门为运营商、政府、军队、教育、大型…...

编程日记 2023/8/18 2:11:57

应用升级/灾备测试时使用guarantee 闪回点迅速回退

1.场景应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。相对于RMAN恢复需要很长时间， 数据库闪回只需要几分钟。 2.技术实现数据库设置 2个db_recovery参数创建guarantee闪回点，不需要开启数据库闪回。…...

编程新知 2026/1/14 22:12:47

树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频

使用rpicam-app通过网络流式传输视频使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素文章来源： http://raspberry.dns8844.cn/documentation 原文网址使用 rpicam-app 通过网络流式传输视频本节介绍来自 rpica…...

编程新知 2025/11/5 13:03:58

AI Agent与Agentic AI：原理、应用、挑战与未来展望

文章目录一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程三、AI Agent的核心技术栈解密3.1 感知模块代码示例：使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例：使用OpenAI GPT-3进…...

编程新知 2026/1/23 7:04:53

Java线上CPU飙高问题排查全指南

一、引言在Java应用的线上运行环境中，CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时，通常会导致应用响应缓慢，甚至服务不可用，严重影响用户体验和业务运行。因此，掌握一套科学有效的CPU飙高问题排查方法&…...

编程新知 2025/11/2 5:30:15

9-Oracle 23 ai Vector Search 特性知识准备

很多小伙伴是不是参加了免费认证课程（限时至2025/5/15） Oracle AI Vector Search 1Z0-184-25考试，都顺利拿到certified了没。各行各业的AI 大模型的到来，传统的数据库中的SQL还能不能打，结构化和非结构的话数据如何和…...

编程新知 2026/2/7 23:29:43

vue3 daterange正则踩坑

<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...

编程新知 2025/12/27 19:12:09

在RK3588上搭建ROS1环境：创建节点与数据可视化实战指南

在RK3588上搭建ROS1环境：创建节点与数据可视化实战指南背景介绍完整操作步骤1. 创建Docker容器环境2. 验证GUI显示功能3. 安装ROS Noetic4. 配置环境变量5. 创建ROS节点（小球运动模拟）6. 配置RVIZ默认视图7. 创建启动脚本8. 运行可视化系统效果展示与交互技术解析ROS节点通…...

编程新知 2025/7/7 1:11:39

数据库正常，但后端收不到数据原因及解决

从代码和日志来看，后端SQL查询确实返回了数据，但最终user对象却为null。这表明查询结果没有正确映射到User对象上。在前后端分离，并且ai辅助开发的时候，很容易出现前后端变量名不一致情况，还不报错，只是单…...

编程新知 2026/1/1 2:56:38

Selenium 查找页面元素的方式

Selenium 查找页面元素的方式 Selenium 提供了多种方法来查找网页中的元素，以下是主要的定位方式： 基本定位方式通过ID定位 driver.find_element(By.ID, "element_id")通过Name定位 driver.find_element(By.NAME, "element_name"…...

编程新知 2026/1/26 17:29:39

【QT控件】显示类控件

目录一、Label 二、LCD Number 三、ProgressBar 四、Calendar Widget QT专栏：QT_uyeonashi的博客-CSDN博客一、Label QLabel 可以用来显示文本和图片. 核心属性如下代码示例: 显示不同格式的文本 1) 在界面上创建三个 QLabel 尺寸放大一些. objectName 分别…...

编程新知 2026/2/4 18:27:37